一种插齿机电子螺旋导轨运动控制方法与流程

本发明涉及一种插齿机电子螺旋导轨运动控制方法，适用于万能式插齿机螺旋导轨的力矩电机的控制。

背景技术：

在现有的普通插齿机上，一般只能加工直齿轮，若需要加工螺旋齿轮，必须增加一套机械螺旋导轨附件，该附件很复杂，制造难度大，并且一套螺旋导轨只能适应一种螺旋角。为了使插齿机能加工任意螺旋角的斜齿轮，一种万能式电子螺旋导轨插齿机应运而生，万能式插齿机用力矩电机代替机械式固定角度的螺旋导轨。针对不同螺旋角度的齿轮，可以通过齿轮参数计算力矩电机的螺旋曲线表，得到力矩电机的控制程序，从而实现任意角度的螺旋齿轮的插齿加工。由于电子螺旋导轨的应用在国内处于起步阶段，针对电子螺旋导轨的控制方法尚不够成熟。

技术实现要素：

基于以上问题，本发明提出了一种插齿机电子螺旋导轨运动控制方法，实现了电子螺旋导轨的正确控制，并能计算出高效的电子螺旋导轨运行程序。该控制方法简单可靠，经自适应计算后程序执行效率高。

为解决上述技术问题，本发明所采用的技术方案是：

一种插齿机电子螺旋导轨运动控制方法，插齿机曲柄运动的角度为主电机旋转角度a，插齿机刀轴螺旋运动的角度为力矩电机的旋转角度φ，主电机旋转角度a与力矩电机旋转角度φ呈实时非线性关系，用函数f＝F(a)表示；主电机旋转角度a为主动值，其取值为离散的非等差数列，力矩电机的旋转角度φ为跟随值，通过在数控系统中建立主电机旋转角度与力矩电机旋转角度的周期性曲线表，用以控制插齿机电子螺旋导轨的运动。

所述非线性函数关系式为：

$f=F(a,b)=\frac{l_2\cos b-l_1\cos a-l_2+l_1}{p}$

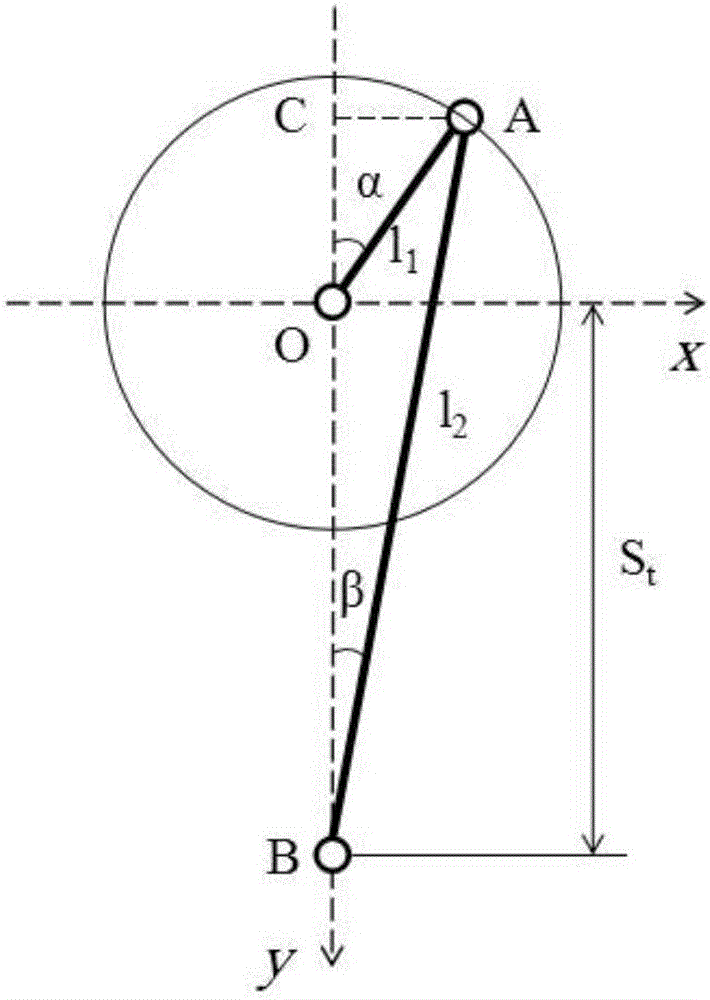
式中，f为力矩电机的旋转角度；F为非线性关系函数；a为主电机旋转角度，是曲柄与运动坐标系Y轴的角度，即∠AOC；b为连杆Y轴的角度，即∠ABC；l₁为曲柄长度，即AO的距离；l₂为连杆长度，即AB的距离；p为电子螺旋导轨的节距；S_t为插齿机刀轴运动的实时位置。

所述主电机旋转角度a的取值为离散的非等差数列，相邻的两个角度值(a_i,f_i)和(a_i+1,f_i+1)通过拟合直线代替原始的曲线，通过不断改变a_i+1的取值，直到拟合直线与曲线之间的误差满足公差要求，此时的a_i+1取值，即为经过自适应计算后的主电机旋转角度值。

本发明一种插齿机电子螺旋导轨运动控制方法，优点在于：

1)、本发明提出了一种插齿机电子螺旋导轨运动控制算法，特别适用于万能式插齿机螺旋导轨的力矩电机的控制，控制方法简单可靠。

2)、本发明中所述的算法具备自适应计算功能，能有效的降低电子螺旋导轨曲线表中点的数量，提高数控程序的执行效率。

3)、本发明中所述的电机旋转角度a，以最优的取值，满足最小程序段数和齿轮螺旋精度要求，提高加工效率和加工质量。

附图说明

下面结合附图和实施例对本发明作进一步说明：

图1为本发明的电子螺旋导轨示意图。

图2为本发明的电子螺旋导轨运动原理图。

图3为本发明的主电机角度自适应计算流程图。

图4为本发明的误差计算示意图。

图5为本发明的力矩电机旋转角度的周期性曲线表。

具体实施方式

如图1-2所示，一种插齿机电子螺旋导轨运动控制方法，实现了电子螺旋导轨的正确控制，并能计算出高效的电子螺旋导轨运行程序。

插齿机曲柄运动的角度为主电机旋转角度a，插齿机刀轴螺旋运动的角度为力矩电机的旋转角度φ，主电机旋转角度a与力矩电机旋转角度φ呈实时非线性关系，用函数f＝F(a)表示；主电机旋转角度a为主动值，其取值为离散的非等差数列，力矩电机的旋转角度φ为跟随值，通过在数控系统中建立主电机旋转角度与力矩电机旋转角度的周期性曲线表，用以控制插齿机电子螺旋导轨的运动。

所述的非线性函数关系式为：

$f=F(a,b)=\frac{l_2\cos b-l_1\cos a-l_2+l_1}{p}$

式中，f为力矩电机的旋转角度；F为非线性关系函数；a为主电机旋转角度，是曲柄与运动坐标系Y轴的角度，即∠AOC；b为连杆Y轴的角度，即∠ABC；l₁为曲柄长度，即AO的距离；l₂为连杆长度，即AB的距离；p为电子螺旋导轨的节距；S_t为插齿机刀轴运动的实时位置。

由图2可知，

$l_2\cos b=\sqrt{{l_2}^2-{\left(l_1\sin a\right)}^2}$

则上述的双变量的非线性函数关系式可变为如下单变量函数。

$f^{\′}=F\left(a\right)=\frac{\sqrt{{l_2}^2-{\left(l_1\sin a\right)}^2}-l_1\cos a-l_2+l_1}{p}$

所述的主电机旋转角度a的取值为离散的非等差数列，其角度取值计算流程如下：

(1)设某一起始点为a_i，则根据上述单变量非线性函数可计算出对应的f'_i；

(2)初始化a_i+1的取值，令a_i+1＝a_i+5；

(3)计算出在a_i+1点力矩电机f'_i+1的值；

(4)根据相邻的两个角度值(a_i,f'_i)和(a_i+1,f'_i+1)，拟合直线EF代替原始的曲线；

(5)取两个相邻角度的中间值计算误差GH的值，图4为本发明的误差计算示意图。若满足以下不等式，ΔT-0.01<GH<ΔT+0.01，则a_i+1取值结束。若不满足以上不等式，则根据图3中的GH精度标准要求返回到第(3)步。

(6)结束a_i+1取值计算。

其中GH为误差，ΔT为误差阈值，-0.01和0.01为误差公差帯。

通过以上流程不断改变a_i+1的取值，直到拟合直线与曲线之间的误差满足公差要求，此时的a_i+1取值即为经过自适应计算后的主电机旋转角度值。经过此方法计算出来的主电机取值点较少，生成的数控代码数量小，数控系统执行效率高。

以上所述的具体实施例，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例而已，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。