基于压缩感知时间调制阵列的DOA估计方法与流程

本发明属于信号处理技术领域，涉及一种时间调制阵列的DOA估计方法，具体涉及一种基于压缩感知的时间调制阵列的DOA估计方法，可用于处理快拍数少，密切索引或者信号相干的时间调制阵列天线高分辨DOA估计。

背景技术：

随着电子与通信技术的快速发展，各种电子系统对天线或天线阵提出越来越苛刻的要求，如高增益、低副瓣、宽频带、低交叉极化分量等，有时甚至是几种苛刻要求的组合。这些对阵列天线特性参量的严格要求往往又对天线阵的结构精度、馈电网络的馈电精度、激励动态范围等提出极为苛刻的，有些甚至是不现实的要求。为了解决上述问题，二十世纪六十年代提出了时间调制天线阵的概念。在时间调制天线阵中，每个元件与高速射频开关(RF)开关连接，其可以通过特定的时间序列人工控制。通过在时间调制阵列中使用时间参数，可以显著降低低/超低副瓣电平(SLL)振幅激励的较高动态范围比，从而缓解设计馈电网络的难度。

作为信号处理领域的重要分支，阵列信号处理在近几十年受到了国内外学者的广泛关注并得到迅速发展，其应用已经遍及雷达、通信、声呐、勘探、射电天线等各个领域。而空间信号到达方向DOA的估计问题是阵列信号处理领域的一个非常重要的研究内容。DOA估计的基本问题就是确定同时处在空间某一区域内多个感兴趣的信号的空间位置，即各个信号到达阵列参考阵元的方向角，简称波达方向。

然而，目前为止人们对时间调制阵列的DOA估计采用的是MUSIC算法和ESPRIT算法，即4D-MUSIC算法和4D-ESPRIT算法。他们利用时间调制均匀阵列中不同边带处的接收信号组成接收数据空间，再将这些信号下变频到同一中频(IF)级之后，利用MUSIC算法或者ESPRIT算法实现DOA估计。但是这些算法受限于奈奎斯特定理，且在处理快拍数少，密切索引，信号相干等问题时性能并不令人满意。虽然有专家和学者提出了大量的解相干和性能优化算法，但在求解过程中需要对天线阵列接收数据的协方差矩阵进行特征值分解，一旦天线阵元数较多，将会出现计算任务过于繁重的问题。

而在2006年，Candes等人提出了一种关于稀疏信号采集和恢复的新理论即压缩感知理论。它充分利用信号稀疏性或可压缩性，在信号采样的同时对数据进行适当的压缩，这大大减轻了数据传输、存储、处理的负担。与传统的奈奎斯特采样理论相比，它只要信号是可压缩或者在某个变换域是稀疏的就可以用远少于经典采样理论所需的测量数据就能精确恢复原始信号或估计出信号的参数。在这个理论框架下，采样速率不取决于信号的带宽，而取决于信息在信号中的结构和内容。在压缩感知理论进行DOA估计中，人们利用阵列信号的空域稀疏性，将DOA估计问题视为过完备原子库下的系数表示恢复问题，通过对角度空间离散化建立稀疏重建模型，然后使用二阶锥规划求解相应的优化问题，然后得到高分辨估计。然而现有的时间调制阵列的DOA估计并未使用压缩感知理论对其进行研究。

技术实现要素：

本发明的目的在于针对上述已有技术的不足，提供了一种基于压缩感知时间调制阵列的DOA估计方法，用于解决现有时间调制阵列的DOA估计方法在处理少量快拍，密切索引或信号相干的问题时估计精度低的技术问题。

本发明的技术思路是：利用差分进化算法对脉冲起始时刻和脉冲持续时间进行优化，建立边带信号模型，同时使用压缩感知理论，通过合理构造基于压缩感知的时间调制阵列稀疏恢复问题模型，充分利用稀疏重构方法的高分辨特性，实现在少量快拍，密切索引或信号相干时较高精度的目标信号的来波方向角度估计。

根据上述技术思路，实现本发明目的采取的技术方案包括如下步骤：

(1)以中心频率方向图的副瓣电平SLL_d、第一边带电平SBL_d和波瓣宽度BW_d为优化目标，使用差分进化算法对控制时间调制阵列单元导通状态的脉冲起始时刻τ₀₀和脉冲持续时间τ₀进行优化，得到优化后脉冲起始时刻τ_0f和优化后脉冲持续时间τ_f；

(2)将优化后脉冲起始时刻τ_0f和优化后脉冲持续时间τ_f代入时间调制阵列输出的和信号表达式中，并对其进行傅里叶展开，再利用展开的结果建立边带信号接收模型X＝B^TAs+N₁，其中，B^T是时间复矩阵B的转置，A为阵列流型矩阵，s是空间入射信号矩阵，N₁为噪声矩阵；

(3)对边带信号接收模型X＝B^TAs+N₁中的阵列流型矩阵A进行扩展稀疏化，形成过完备冗余字典并利用冗余字典将边带信号接收模型X＝B^TAs+N₁转化为时间调制阵列边带信号稀疏接收模型其中，为稀疏信号向量；

(4)对时间调制阵列边带信号稀疏接收模型中的X进行奇异值分解和降维处理，得到低维度边带信号X_SV、入射信号和噪声信号N_SV；

(5)利用低维度边带信号X_SV、入射信号和噪声信号N_SV，将时间调制阵列边带信号稀疏接收模型改写成并对其进行转变，得到基于压缩感知的时间调制阵列稀疏恢复问题模型；

(6)将基于压缩感知的时间调制阵列稀疏恢复问题模型转化为二阶锥规划问题，并利用凸优化包对该二阶锥规划问题进行求解，得到恢复向量再寻找出该恢复向量中的非零位置，即得到目标信号的来波方向角度。

本发明与现有技术相比，具有以下优点：

本发明由于在获取目标DOA角度时，采用了压缩感知理论，充分利用了稀疏重构方法的高分辨特性，与现有技术相比，在少量快拍，密切索引或信号相干的情况下有效地提高了目标波达方向DOA估计精度。

附图说明

图1是本发明的实现流程图；

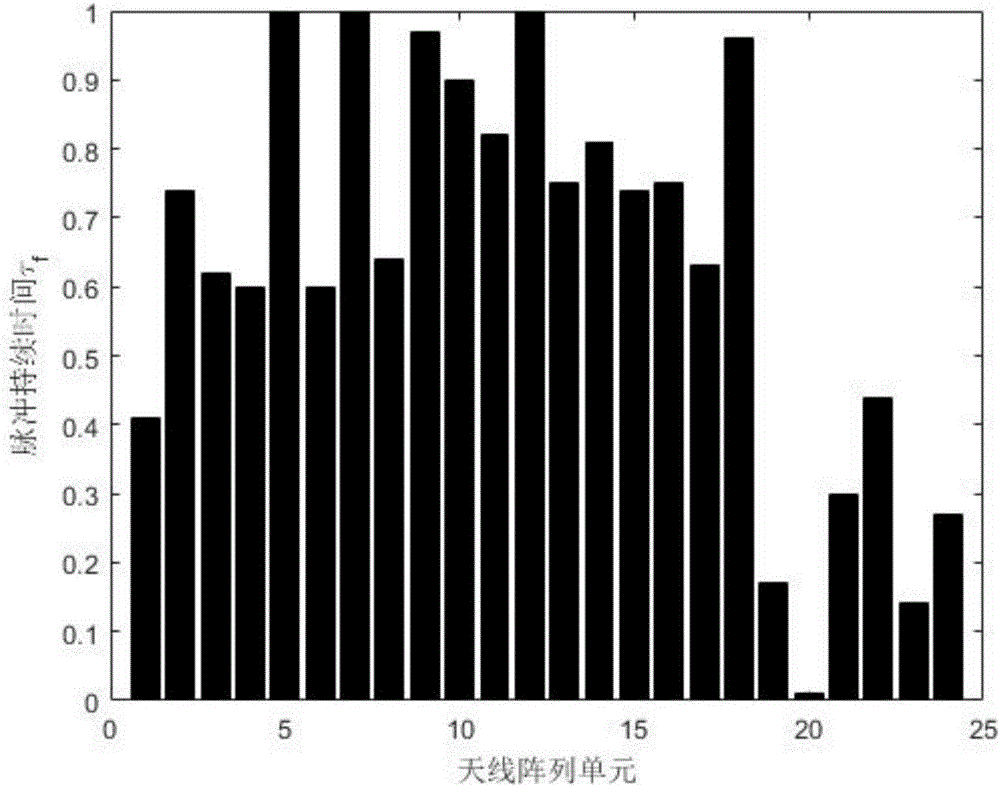
图2是本发明的实施例中脉冲工作时序图；

图3是本发明的实施例中算法性能随快拍数变化情况图；

图4是本发明与现有技术对于三个不相关目标信号波达方向角度估计均方误差随信噪比的变化关系图；

图5是本发明与现有技术对于三个相关目标信号波达方向角度估计的均方误差随信噪比变化关系图；

图6是本发明与现有技术在两个不相关目标信号波达方向角度估计的均方误差与角度间隔的关系图。

具体实施方式

以下结合附图和具体实施例，对本发明的目的、技术方案和优点进行详细描述。显然，基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都属于本发明保护的范围。

参照图1，一种基于压缩感知的时间调制阵列的DOA估计方法，实现步骤如下：

步骤1，使用差分进化算法对控制时间调制阵列单元导通状态的脉冲起始时刻τ₀₀和脉冲持续时间τ₀进行优化，具体步骤如下：

步骤1a，确定最大循环次数以及种群规模SN，并对种群个体Y_ij进行初始化，其中，i表示第i个个体，i＝1,2,…,SN，j表示第j个优化分量，j＝1,2,…,D，D为待优化变量数；

步骤1b，计算种群个体Y_i,G的适应度fit_i：

其中，f(Y_i,G)＝ω₁·max|SLL_max-SLL_d|+ω₂·|Bw₀-Bw_d|+ω₃·U(SBL_max-SBL_d)是第G代种群的第i个个体的目标函数值，BW₀，SLL_max及SBL_max分别表示种群个体Y_i,G的中心频率处的零点主波瓣宽度，最大副瓣电平以及第一边带频率处的最大边带电平，ω₁，ω₂，ω₃分别为权重系数；

步骤1c，对个体Y_i,G进行变异操作，得到变异后的个体V_i,G+1：

V_i,G+1＝Y_r1,G+F·(Y_r2,G-Y_r3,G)

其中，r₁,r₂,r₃∈{1,2,…,SN}，r₁,r₂,r₃随机选取，且满足i≠r₁≠r₂≠r₃，F为变异因子；

步骤1d，对经过变异后的个体V_i,G+1进行交叉操作，得到试验个体U_i,G+1：

U_i,G+1＝(u_1i,G+1,u_2i,G+1,…u_Di,G+1)

其中，rand(j)是[0,1]内的随机数，CR为交叉因子，rnbr(i)∈{1,2,…,D}，rnbr(i)随机选取；

步骤1e，计算试验个体U_i,G+1的适应度函数值fit_i′，并与Y_i,G的适应度函数值fit_i进行对比，选择适应度函数值高的种群个体作为下一代种群个体Y_i,G+1：

步骤1f，重复执行步骤(1b)～步骤(1e)，直至满足优化目标要求或完成最大循环次数时，跳出循环并输出新的种群最优位置G_b'完成优化，其中，G'_b＝[τ_0fτ_f]，即τ_0f为优化后脉冲起始时刻和τ_f为优化后脉冲持续时间；

步骤2，建立边带信号接收模型，具体步骤如下：

步骤2a，设定时间调制阵列参数：阵元数目为M，快拍数为N，空间远场信号源数为K，载波频率为f₀，单元间隔为d，高速射频开关周期为T_p，最高阶边带的阶数为Q；

步骤2b，将优化后脉冲起始时刻τ_0f和优化后脉冲持续时间τ_f代入时间调制阵列输出的和信号表达式x(t)：

其中，U_m(t)为第m个天线单元高速射频开关周期性开关函数，其表达式与时间调制阵列的调制方式及控制时间调制阵列单元导通状态的脉冲起始时刻τ_0m和持续时间τ_m有关，τ_0m∈τ_0f，τ_m∈τ_f，s_k(t)为第k个空间远场信号源所发射的信号，θ_k为第k个空间远场信号源所在的空间角度，β＝2π/λ，λ为波长，n_m(t)表示第m个天线单元的噪声，并假设噪声为零均值的高斯白噪声，其方差为σ²，各个天线单元间的噪声统计不相关，噪声与信号也统计不相关；

步骤2c，对x(t)进行傅立叶级数展开，得第q阶边带信号表达式x_q(t)：

其中，为第m个阵元在第q阶边带的时间复激励，f_p＝1/T_p；

步骤2d，对x_q(t)进行下变频处理，得到下变频后的第q阶边带信号表达式x'_q(t)：

其矩阵形式的表达式为：

X(n)＝B^T[As(n)+N(n)],n＝1,2,…,N，

其中，X(n)＝[x'_-Q(n)x'_-Q+1(n)…x'_q(n)…x'_Q(n)]^T为由各个边带信号组成的快拍列向量，s(n)＝[s₁(n)s₂(n)…s_k(n)…s_K(n)]^T为空间入射信号列向量，s_k(n)表示s_k(t)的基带采样信号，N(n)＝[n₁(n)n₂(n)…n_N(n)]^T为M×1维噪声列向量；

当快拍数为N时，边带信号矩阵形式的表达式可表述为边带信号接收模型：

X＝B^TAs+N₁

其中X＝[X(1)X(2)…X(N)]，s＝[s(1)s(2)…s(N)]，N＝[N(1)N(2)…N(N)]，N₁＝B^TN；

步骤3，对边带信号接收模型X＝B^TAs+N₁中的阵列流型矩阵A进行扩展稀疏化，具体步骤如下：

步骤3a，将整个空间划分为N_θ份，即并假设划分的每个角度都对应一个潜在的信号源且实际存在的K个信号源所在角度恰好都落在划分的网格上，则阵列流型A可扩展成一个过完备集

步骤3b，在稀疏表示框架下，将边带信号接收模型X＝B^TAs+N₁转变成时间调制阵列稀疏信号接收模型为：

其中中只存在信号的K个位置的元素值是非零的，其他N_θ-K个位置的元素值均为0，于是稀疏信号向量为K稀疏矩阵；

步骤4，对时间调制阵列边带信号稀疏接收模型中的X进行奇异值分解和降维处理，具体步骤如下：

步骤4a，对X进行奇异值分解X＝UΛV^H，得到奇异值矩阵Λ、左奇异值向量矩阵U、右奇异值向量矩阵V；

步骤4b，利用右奇异值向量矩阵对X进行降维处理，得到降维之后的矩阵X_SV＝XVD_K，其中D_K＝[I_K 0]，I_K表示K×K单位矩阵，0表示K×(N-K)维的零矩阵，同理可得和N_SV＝N₁VD_K；

步骤5，基于压缩感知的时间调制阵列稀疏恢复问题模型，其获取步骤为：

步骤5a，对时间调制阵列稀疏信号接收模型左右同乘VD_K，得到新的时间调制阵列稀疏信号接收模型:

由于中的元素与冗余字典的各列一一对应，即与信号的来波一一对应，由其中非零元素位置可唯一确定源信号对应的入射角度。因此只要利用稀疏重构算法精确恢复信号即可得到信号的DOA估计。因为与具有相同的稀疏性，则冗余字典可以使DOA的角度参数估计转化为求解的问题，此时，新的时间调制阵列稀疏信号接收模型可以看作为L1范数约束的最优化问题：

其中，ε是一个与噪声水平有关的参数，||·||₁、||·||₂分别表示L1范数和L2范数；

步骤5b，L1范数约束的最优化问题利用拉格朗日乘子法可进一步改写为基于压缩感知的时间调制阵列稀疏恢复问题模型：

其中η为超参数，用于控制信号稀疏度和残差之间的权衡；

步骤6，目标信号的来波方向角度，其获取步骤为：

将基于压缩感知的时间调制阵列稀疏恢复问题模型的求解转化为二阶锥规划问题为：

其中η为超参数，使用凸优化软件包求解构造出的稀疏恢复问题中的恢复向量恢复向量中非零元素的位置即代表目标信号的来波方向角度。

以下结合仿真实验，对本发明的技术效果作进一步详细说明：

1、实验条件和内容：

假设时间调制天线为均匀直线阵，阵元间隔为半个波长，目标数目已知，空间网格统一为0.1°，从-90°到90°范围，阵元数M＝24，f₀＝300MHz，T_p＝1s，边带Q＝10，采用基于阵列可变口径尺寸(VAS)的时间调制方式，副瓣电平SLL_d＝-30dB、第一边带电平SBL_d＝-20dB和波瓣宽度BW_d＝70，ω₁＝1.2，ω₂＝0.1，ω₃＝0.3，最大循环次数500以及种群规模24，利用差分进化算法优化所得时间序列如图2所示；

1.1、假设空间远场有1个信号源，入射角度为30°，快拍数从1到20以2为间隔进行变化，信噪比SNR为20dB，每个快拍数处做50次蒙特卡罗实验，得到对1个目标信号波达方向角度估计的均方误差随快拍数变化关系，如图3所示；

1.2、假设空间远场有3个互不相干的信号源，入射角度分别为-12°、-2°、30°，快拍数取N＝50，信噪比SNR从-10dB到20dB以5dB为间隔进行变化，每个信噪比下做50次蒙特卡罗实验，得到对三个不相关目标信号波达方向角度的估计均方误差随信噪比的变化关系，如图4所示；

1.3、假设空间远场有3个相干的信号源，入射角度分别为-12°、-2°、30°，快拍数取N＝50，信噪比SNR从-10dB到20dB以5dB为间隔进行变化，每个信噪比下做50次蒙特卡罗实验，得到对三个相干目标信号波达方向角度的估计均方误差随信噪比的变化关系，如图5所示；

1.4、假设空间远场有个信号源，入射角θ₁＝15°，θ₂＝θ₁+Δθ，Δθ∈[-5°,5°]，信噪比SNR为10dB，得到对两个不相关目标信号波达方向角度估计的均方误差与角度间隔的关系，如图6所示；

2、仿真结果分析：

参照图2，由于在本实验中采用的是VAS调制方式，则控制时间调制阵列单元导通状态的脉冲起始时刻τ₀₀为0，此时纵坐标即表示经过差分进化算法优化得到的结果即为优化后的脉冲持续时间τ_f。

参照图3，当快拍数为1时，本发明的算法对目标信号波达方向角度估计均方误差已经达到了0.4以下，当快拍数达到10时均方误差已经趋近于0，说明本发明突破了奈奎斯特定理，能够在少快拍甚至是单快拍时实现目标信号波达方向角度精确估计。

参照图4，两种算法在信号非相干、角度间距较大时随着信噪比SNR的变化，具有相近的均方误差，当SNR达到0时均方误差已趋近于0，说明二者在在信号非相干、角度间距较大情况下都能对目标信号波达方向角度估计进行正确估计，且具有相近的估计性能。

参照图5，当信号相干时，4D-MUSIC算法随着信噪比SNR的增加，对目标信号波达方向角度估计均方误差依然很大，说明当信号相干时，即使增加信噪比也不能4D-MUSIC算法的估计精度有所改善，而本发明算法在SNR＝-5dB时其对目标信号波达方向角度估计的均方误差以趋于0，说明即使是在信号相干的情况下，本发明算法依然能够精确估计出目标信号波达方向角度。

参照图6，4D-MUSIC算法在信号间隔|Δθ|≥2°时能够分辨出相邻目标，而本发明的在角度间隔为0.2°时对两相邻目标信号波达方向角度估计的均方误差已趋于稳定，说明本发明在。

从图3～图6,可以看出，本发明能够实现对目标信号波达方向角度的估计，且在快拍数少，密切索引，信号相干的情况下依然具有较高的估计精度。

以上实施例仅用以说明本发明在均匀直线阵列以及基于VAS调制方式的时间调制阵列中的可行性，而非对其限制；尽管参照前述实施例对本发明实施步骤进行了详细地说明，本领域的普通技术人员应当理解：其依然可以对前述具体实施方式进行修改或者对其中部分或者全部技术特征进行等同替换，而这些修改或者替换，并不使相应技术方案的本质脱离本发明技术方案的范围。