基于杂波空时等效的三维异构阵空时重构方法与流程

本发明属于雷达技术领域，尤其涉及一种基于杂波空时等效的三维异构阵空时重构方法，用于机载共形阵雷达信号处理。

背景技术：

现代战争对机载雷达的隐身能力、机动能力和目标探测能力都提出了越来越高的要求，而机载雷达采用的天线，或外露于机体，或装于流线形的整流罩内，从机头到机尾分布着多达几十种类型各异的天线，这不仅大大影响了飞机的气动性能和隐身性能，而且也限制了很多电子设备的性能。因此，研究能够与飞行载体表面相吻合的天线系统-三维异构阵，成为近年来日益重视的新领域。机载三维阵雷达，由于其便于集成，能减小载机负荷和雷达散射截面积等独特优势，成为相控阵雷达的重要发展方向。

早在20世纪60年代，国外就已经开始了对三维异构阵的研究，包括美国、以色列、日本和欧洲。例如，美国空军提出的宇航飞行器“智能蒙皮计划”(penval)，其本质就是将多副天线与飞行器载体有效共形的研究计划。我国在20世纪90年代也开始进行了研究。目前，三维异构阵已受到各国军方的高度关注，并且已有世界顶级战机、预警机采用了三维异构阵以支持其先进的机载雷达和卓越的气动-隐身外形。

但是，不同于平面相控阵，三维异构阵接收的杂波特性将变得十分复杂，这种复杂性主要体现在阵元通道间的互耦特性更加复杂、阵元通道间的极化特性更加复杂、阵元/子阵相位中心非线性排列、杂波存在极化去相关问题等，这种杂波特性的复杂性也给杂波抑制带来很大的问题，包括阵列流型更加复杂，目标和杂波的导向矢量计算困难，导向矢量间的相关性更难计算，干扰子空间和目标导向矢量的关系难以确定，杂波秩显著增加等。在杂波抑制性能方面，由于机载雷达的平台运动，在不同的方向，杂波往往都呈现出一定的非平稳性，在近距离探测时这种非平稳性尤其严重，这导致了三维异构阵在形成接收方向图时的旁瓣性能不稳定，使得传统的空时自适应处理算法在三维异构阵雷达的杂波抑制中性能严重下降。

技术实现要素：

针对上述现有技术的缺点，本发明的目的在于提供一种基于杂波空时等效的三维异构阵空时重构方法，能够解决三维异构阵雷达在形成接收方向图时的旁瓣性能不稳定导致的杂波抑制性能下降的问题。

为达到上述目的，本发明采用如下技术方案予以实现。

一种基于杂波空时等效的三维异构阵空时重构方法，所述方法包括如下步骤：

步骤1，设定雷达的三维异构阵为圆台阵，所述圆台阵共包含m层阵元，将每层阵元作为圆台阵的一个子阵，则所述圆台阵包含m个子阵；获取所述圆台阵接收到的杂波回波数据，所述圆台阵接收到的杂波回波数据包含l个距离单元的回波数据矢量；

令l＝1；l表示第l个距离单元，l＝1，2，...，l；

步骤2，获取第l个距离单元的回波数据矢量，将所述第l个距离单元的回波数据矢量重新排列为回波数据矩阵，得到第l个距离单元的回波数据矩阵，所述第l个距离单元的回波数据矩阵为k行m列的矩阵，其中，所述第l个距离单元的回波数据矩阵的第m列表示第m个子阵接收到的回波数据，所述第l个距离单元的回波数据矩阵的第k行表示第k个脉冲时刻接收到的回波数据，m＝1，...，m，k＝1，...，k；m为圆台阵包含的子阵数据，k为雷达在一个相干处理间隔内发射的脉冲个数，且k远大于m；

步骤3，对所述第l个距离单元的回波数据矩阵中的第m个子阵接收到的回波数据分别做m-m个元素的循环向上移动，且m分别取1，2，...，m；得到第l个距离单元的重排后的回波数据矩阵；

步骤4，删除所述第l个距离单元的重排后的回波数据矩阵中相位不一致的后m-1行，得到第l个距离单元的空时重构回波数据，所述第l个距离单元的空时重构回波数据为k-m+1行m列；

步骤5，令l的值加1，并依次重复执行步骤2至步骤4，分别得到l个距离单元中每个距离单元的空时重构回波数据。

本发明技术方案的特点和进一步的改进为：

(1)在步骤5之后，所述方法还包括：

步骤6，对所述第l个距离单元的空时重构回波数据中的第k′个多普勒通道数据作离散傅里叶变换，得到第l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据，其中，k′依次取1，2，...，k-m+1，从而得到第l个距离单元的空时重构回波数据中k-m+1个多普勒通道离散傅里叶变换后的数据；

步骤7，令l分别取1，2，...，l，从而得到l个距离单元中每个距离单元的空时重构回波数据中k-m+1个多普勒通道离散傅里叶变换后的数据；

步骤8，对l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据进行空域滤波，令k′依次取1，2，...，k-m+1，得到l个距离单元的空时重构回波数据的滤波结果，并将所述l个距离单元的空时重构回波数据的滤波结果作为杂波抑制结果。

(2)步骤2中，

获取第l个距离单元的回波数据矢量xl为：xl＝[x11，x12，...，x1m；x21，x22，...，x2m；...，xkm，...；xk1，xk2，...，xkm]^t；

其中，[·]^t表示转置操作，xkm为第k个脉冲时刻第m个子阵的回波数据，且

其中，i＝1，...，i表示回波数据中的第i个杂波块，i为第l个距离单元内的杂波块数目，ai表示第i个杂波块的幅度，fsi表示第i个杂波块的归一化空间频率，fdi表示第i个杂波块的归一化多普勒频率；

且第i个杂波块的归一化空间频率第i个杂波块的归一化多普勒频率其中，d为子阵间距，φa为天线锥角，λ为雷达工作波长，v为平台速度，t为脉冲重复间隔；

令第i个杂波块的归一化空间频率与第i个杂波块的归一化多普勒频率相等，则平台速度v、脉冲重复间隔t以及子阵间距d存在如下关系d＝2vt。

(3)步骤2中，

将所述第l个距离单元的回波数据矢量xl重新排列为回波数据矩阵，得到第l个距离单元的回波数据矩阵xl，具体为：

其中，xl∈c^k×m，c^k×m表示k行m列的复数矩阵，且xl的行表示时域回波数据，xl的列表示空域回波数据；

令第i个杂波块的归一化空间频率与第i个杂波块的归一化多普勒频率相等时，第l个距离单元的回波数据矩阵xl为：

(4)步骤3中，对所述第l个距离单元的回波数据矩阵中的第m个子阵接收到的回波数据分别做m-m个元素的循环向上移动，具体为：

对第l个距离单元的回波数据矩阵xl的第m列的回波数据元素做m-m个元素的循环向上移动，从而得到第l个距离单元的重排后的回波数据矩阵

其中，c^k×m表示k行m列的复数矩阵。

(5)步骤4中，删除所述第l个距离单元的重排后的回波数据矩阵中相位不一致的后m-1行，得到第l个距离单元的空时重构回波数据为：

其中，表示行m列的复数矩阵，且

(6)步骤6具体为：

(6a)构造与所述第l个距离单元的空时重构回波数据相对应的变换矩阵f：

其中，表示行列的复数矩阵；

(6b)所述变换矩阵f的第k′列fk′：k′表示第k′个多普勒通道；

(6c)对所述第l个距离单元的空时重构回波数据中的第k′个多普勒通道数据作离散傅里叶变换，得到第l个距离单元的空时重构回波数据中第k′个多普勒通道数据

其中，c^1×m表示1行m列的复数矩阵；

(6d)令k′依次取1，2，...，k-m+1，重复执行子步骤(6b)和(6c)，从而得到第l个距离单元的空时重构回波数据中k-m+1个多普勒通道数据。

(7)步骤8具体为：

(8a)获取l个距离单元的空时重构回波数据中第k′个多普勒通道数据yk′：其中，yk′∈c^m×l，c^m×l表示m行l列的复数矩阵，表示第l个距离单元的空时重构回波数据中第k′个多普勒通道数据，(·)^t表示转置操作；

(8b)采用如下约束表达式，求解最优滤波权向量w：

其中，e{·}表示求期望运算，为第k′个多普勒通道的回波协方差矩阵，s为空时导向矢量；

求解上述约束表达式，得到最优滤波权向量w＝λr^-1s，其中，λ＝1/(s^hr^-1s)；(·)^h表示共轭转置操作，(·)^-1表示求逆操作，||·||²表示求模值平方操作；

(8c)根据所述最优滤波权向量w对l个距离单元的空时重构回波数据中第k′个多普勒通道数据yk′进行空域滤波，得到第k′个多普勒通道的滤波输出yk′＝w^hyk′；

(8d)令k′依次取1，2，...，k-m+1，重复执行子步骤(8a)至(8c)，得到l个距离单元的空时重构回波数据的滤波结果。

本发明与现有技术相比具有以下优点：

(1)三维异构阵是三维天线结构，由于其在方位向和俯仰向的非线性结构、通道幅相误差等原因，形成接收方向图时旁瓣水平抬升，经脉冲-多普勒滤波后造成相应的旁瓣杂波剩余功率增加，对杂波抑制性能也是不利的。本发明采用基于杂波空时等效的三维异构阵空时重构方法，可以将三维阵列等效为平面阵列，改善杂波的抑制性能；(2)机载雷达存在平台运动，这将导致三维阵的某一空间位置不能接收所有的脉冲回波，引起杂波的多普勒频谱展宽。本发明将原始回波数据进行空时重构处理，当载机速度与脉冲重复间隔满足dpca条件时，可以达到所有阵元在同一时刻的相位一致，使得杂波相消结果更稳定、更彻底，从而提高了杂波区的抑制性能；(3)本发明并未局限于理想条件，在平台速度不稳定即不满足dpca条件的情况下，其改善性能仍然优于传统滤波方法，大大扩展了本发明的应用场合。本发明的基于杂波空时等效的三维异构阵空时重构方法不仅可以应用于杂波抑制处理，也可以应用于目标检测领域。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

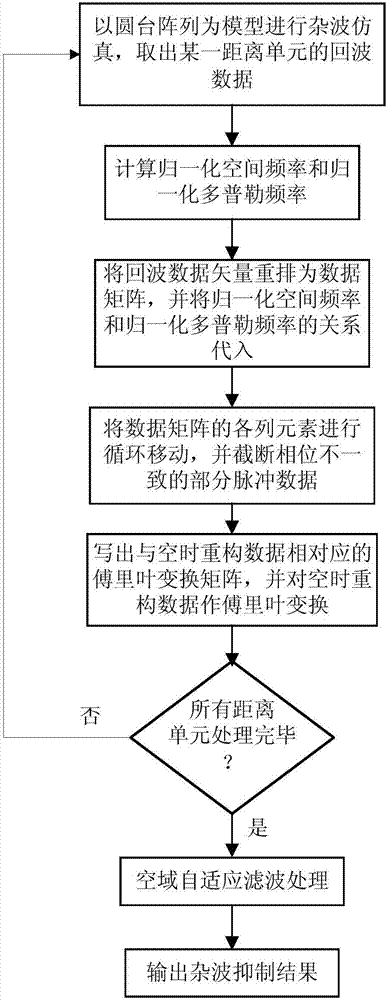
图1为本发明实施例提供的基于杂波空时等效的三维异构阵空时重构方法的流程示意图；

图2为本发明实施例提供的圆台阵的数据空时重构示意图；

图3为本发明实施例提供的对原始回波数据与本发明空时重构数据作stap杂波抑制后的平均杂波剩余功率对比曲线示意图；

图4为本发明实施例提供的对原始回波数据与本发明空时重构数据作stap杂波抑制后的改善因子对比曲线示意图；

图5为本发明实施例提供的主杂波区附近的某多普勒通道，对原始回波数据与本发明空时重构数据作stap杂波抑制后的改善因子随dpca比例变化曲线示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明实施例提供一种基于杂波空时等效的三维异构阵空时重构方法，如图1所示，所述方法包括如下步骤：

步骤1，设定雷达的三维异构阵为圆台阵，所述圆台阵共包含m层阵元，将每层阵元作为圆台阵的一个子阵，则所述圆台阵包含m个子阵；获取所述圆台阵接收到的杂波回波数据，所述圆台阵接收到的杂波回波数据包含l个距离单元的回波数据矢量。

令l＝1；l表示第l个距离单元，l＝1，2，...，l。

假设三维异构阵列模型为圆台阵，该圆台共包含m层阵元，每层阵元数量不等，将每一层阵元划分为一个子阵，则可划分为m个子阵，圆台的所有阵元数目为n。子阵间距为d，雷达工作波长为λ，且满足d＝λ/2。平台速度向量为v，其方向为x轴正向，天线轴向与向量v的夹角为0。。雷达在一个相干处理间隔内的发射脉冲数目为k。

步骤2，获取第l个距离单元的回波数据矢量，将所述第l个距离单元的回波数据矢量重新排列为回波数据矩阵，得到第l个距离单元的回波数据矩阵，所述第l个距离单元的回波数据矩阵为k行m列的矩阵，其中，所述第l个距离单元的回波数据矩阵的第m列表示第m个子阵接收到的回波数据，所述第l个距离单元的回波数据矩阵的第k行表示第k个脉冲时刻接收到的回波数据，m＝1，...，m，k＝1，...，k；m为圆台阵包含的子阵数据，k为雷达在一个相干处理间隔内发射的脉冲个数，且k远大于m。

步骤2中，由于这里仅考虑子阵间的相位关系，所以将每一层的各个阵元之间接收信号的相位时延忽略不计。

获取第l个距离单元的回波数据矢量xl为：xl＝[x11，x12，...，x1m；x21，x22，...，x2m；...，xkm，...；xk1，xk2，...，xkm]^t；

其中，[·]^t表示转置操作，xkm为第k个脉冲时刻第m个子阵的回波数据，且

其中，i＝1，...，i表示回波数据中的第i个杂波块，i为第l个距离单元内的杂波块数目，ai表示第i个杂波块的幅度，fsi表示第i个杂波块的归一化空间频率，fdi表示第i个杂波块的归一化多普勒频率；

且第i个杂波块的归一化空间频率第i个杂波块的归一化多普勒频率其中，d为子阵间距，φa为天线锥角，λ为雷达工作波长，v为平台速度，t为脉冲重复间隔；

根据上述公式，可得到归一化空间频率和归一化多普勒频率之间存在如下关系：

fdi＝βfsi

其中β称为归一化坐标的杂波脊斜率，由于天线轴向与速度夹角为零，

则当平台速度v、脉冲重复间隔t与子阵间距d之间满足dpca(displacedphasecenterantenna，偏置相位中心天线)条件时，即d＝2vt，那么在一个脉冲重复间隔内，圆台阵的移动距离为一个子阵间距，此时β＝1，那么得到归一化空间频率与归一化多普勒频率的关系为：

fsi＝fdi

以下推导均以此条件为前提。

令第i个杂波块的归一化空间频率与第i个杂波块的归一化多普勒频率相等，则平台速度v、脉冲重复间隔t以及子阵间距d存在如下关系d＝2vt。

进一步的，以时域为行，空域为列，将所述第l个距离单元的回波数据矢量xl重新排列为回波数据矩阵，得到第l个距离单元的回波数据矩阵xl，具体为：

其中，xl∈c^k×m，c^k×m表示k行m列的复数矩阵，且xl的行表示时域回波数据，xl的列表示空域回波数据；

令第i个杂波块的归一化空间频率与第i个杂波块的归一化多普勒频率相等时，第l个距离单元的回波数据矩阵xl为：

步骤3，对所述第l个距离单元的回波数据矩阵中的第m个子阵接收到的回波数据分别做m-m个元素的循环向上移动，且m分别取1，2，...，m；得到第l个距离单元的重排后的回波数据矩阵。

步骤3中，对所述第l个距离单元的回波数据矩阵中的第m个子阵接收到的回波数据分别做m-m个元素的循环向上移动，具体为：

对第l个距离单元的回波数据矩阵xl的第m列的回波数据元素做m-m个元素的循环向上移动，从而得到第l个距离单元的重排后的回波数据矩阵

其中，c^k×m表示k行m列的复数矩阵。

示例性的，如图2所示，三维圆台阵的外形类似于圆锥形状，圆台轴向为x轴正向，与载机速度方向一致。为方便理解，仅画了示意图，该图中的圆台阵共两层圆环阵，即两个子阵，沿x轴正向的第1个子阵包含2个阵元，第2个子阵包含1个阵元。图中画了3个脉冲重复间隔的时间内圆台阵的运动情况。观察该图可发现，当平台速度满足dpca条件时，在接收脉冲信号的一个脉冲重复间隔内，圆台阵层级的子阵刚好移动一个子阵间距，例如在图2中，圆台阵的第2个子阵刚好与下一个脉冲重复间隔的第1个子阵处于相同的空间位置。

接下来，通过对数据的循环移动和截断处理，使得处在同一个空间位置的各脉冲数据作为同一个时域通道的数据，从而达到同一空间位置的相位一致。具体化为，将数据矩阵xl中的第m个子阵的空域通道数据作m-m个元素的向上循环移动，对于矩阵表达式来说，就是把矩阵的第m列中的各元素作m-m个元素的向上循环移动，其中m＝1，...，m，则数据矩阵的表达式变为：

从上式的矩阵表达式中可以看出，矩阵的第1行至第k-m+1行中各个空域通道数据完成了相位对齐操作。

步骤4，删除所述第l个距离单元的重排后的回波数据矩阵中相位不一致的后m-1行，得到第l个距离单元的空时重构回波数据，所述第l个距离单元的空时重构回波数据为k-m+1行m列。

为实现相位一致，需要保留各个阵元之间相位对齐的部分数据，并对相位不一致的部分脉冲数据进行截断操作，即保留矩阵中的前k-m+1行，最终得到空时重构数据。

步骤4中，删除所述第l个距离单元的重排后的回波数据矩阵中相位不一致的后m-1行，得到第l个距离单元的空时重构回波数据为：

其中，表示行m列的复数矩阵，且

这样，所有空间位置接收的杂波数据达到相位一致，完成了数据的空时重构处理。

步骤5，令l的值加1，并依次重复执行步骤2至步骤4，分别得到l个距离单元中每个距离单元的空时重构回波数据。

步骤6，对所述第l个距离单元的空时重构回波数据中的第k′个多普勒通道数据作离散傅里叶变换，得到第l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据，其中，k′依次取1，2，...，k-m+1，从而得到第l个距离单元的空时重构回波数据中k-m+1个多普勒通道离散傅里叶变换后的数据。

采用fa(factoredapproach，因子化)方法，首先对空时重构数据作傅里叶变换，使得数据从时域转换到多普勒域，然后再对某一多普勒通道的空域数据作自适应滤波处理。

步骤6具体为：

(6a)构造与所述第l个距离单元的空时重构回波数据相对应的变换矩阵f：

其中，表示行列的复数矩阵；

(6b)所述变换矩阵f的第k′列fk′：k′表示第k′个多普勒通道；

(6c)对所述第l个距离单元的空时重构回波数据中的第k′个多普勒通道数据作离散傅里叶变换，得到第l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据

其中，c^1×m表示1行m列的复数矩阵；

(6d)令k′依次取1，2，...，k-m+1，重复执行子步骤(6b)和(6c)，从而得到第l个距离单元的空时重构回波数据中k-m+1个多普勒通道离散傅里叶变换后的数据。

步骤7，令l分别取1，2，...，l，从而得到l个距离单元中每个距离单元的空时重构回波数据中k-m+1个多普勒通道数据。

步骤8，对l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据进行空域滤波，令k′依次取1，2，...，k-m+1，得到l个距离单元的空时重构回波数据的滤波结果，并将所述l个距离单元的空时重构回波数据的滤波结果作为杂波抑制结果。

步骤8具体为：

(8a)获取l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据yk′：其中，yk′∈c^m×l，c^m×l表示m行l列的复数矩阵，表示第l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据，(·)^t表示转置操作；

(8b)采用如下约束表达式，求解最优滤波权向量w：

其中，e{·}表示求期望运算，为第k′个多普勒通道离散傅里叶变换后的的回波协方差矩阵，s为空时导向矢量；w＝[w1，w2，...，wm]^t，且w∈c^m×1。

求解上述约束表达式，得到最优滤波权向量w＝λr^-1s，其中，λ＝1/(s^hr^-1s)；(·)^h表示共轭转置操作，(·)^-1表示求逆操作，||·||²表示求模值平方操作；

(8c)根据所述最优滤波权向量w对l个距离单元的空时重构回波数据中第k′个多普勒通道离散傅里叶变换后的数据yk′进行空域滤波，得到第k′个多普勒通道的滤波输出yk′＝w^hyk′；

(8d)令k′依次取1，2，...，k-m+1，重复执行子步骤(7a)至(7c)，得到l个距离单元的空时重构回波数据的滤波结果。

观察步骤(6c)，对空时重构数据作傅里叶变换后，将这样的数据作杂波相消的抑制结果更稳定、更彻底。这是因为用于估计杂波协方差矩阵的距离样本虽为独立同分布样本，但是针对每个距离单元的数据幅度只是统计意义上的平均水平，不同的距离单元，数据幅度依然存在差距而非完全相等；且不同距离单元、不同杂波块的空间频率也不同。

那么，对原始回波数据进行fa方法处理后的空域自适应滤波处理过程，具体化为，对1号空域通道数据滤波，是利用2号空域通道数据作加权处理并与其进行杂波相消，对每个杂波块来说，相同的权矢量无法保证完全对消，即：xk′l(1)-w^hxk′l(2)≠0；

而将回波数据进行重排、截断处理后，两空域通道数据的幅度、相位一致，总能找到适当的权矢量，将杂波相消的更为彻底，即：

因此，基于杂波空时等效的空时重构方法能够很好的对消旁瓣杂波，同时在主杂波区较传统滤波处理也有较好的抑制性能。

对于空间的所有阵元来说，杂波的时间采样均为同步采样，空间采样仅与空间位置或角度有关，与采样时间无关，类似于时间采样仅与采样时间有关，与空间位置无关，即为所谓的杂波空时等效特性。基于这一特性，当没有平台运动且忽略各种误差的情况下，同一空间采样位置能够接收到所有脉冲信号，且所有阵元在同一时刻的相位一致。而机载雷达存在平台运动，导致三维阵的某一空间位置不能接收所有的脉冲回波，引起杂波的多普勒频谱展宽，那么当载机速度与脉冲重复频率满足dpca条件时，可以利用脉冲之间的转换来补偿平台运动，将空时数据重排，以达到所有阵元在同一时刻的相位一致，并将相位不一致的部分截断使得体阵列转换为面阵列，实现数据的空时重构，提高杂波的抑制性能。

下面结合仿真实验对本发明的效果做进一步说明。

1)仿真参数

本发明是一种基于杂波空时等效的三维异构阵空时重构方法，可用于三维异构阵列的杂波抑制和目标检测。

本发明采用的三维异构阵列模型为圆台形状。圆台阵列共包含6圈阵元，每一圈阵元数量不等，将圆台阵的6圈阵元划分为6个子阵，子阵间距为半波长，初始载机速度满足dpca条件。那么，将以圆台阵列为天线模型的杂波仿真数据进行空时重构后，对于阵列来说，是将圆台形状转换为同心圆环形状。这样便完成了对圆台阵的空时数据重构处理。详细的系统参数参照下表。

2)仿真数据处理结果及分析

为了说明本发明性能的优越性，给出了原始数据作空时自适应处理(spacetimeadaptiveprocessing，stap)杂波抑制以及本发明对空时重构数据作stap杂波抑制的处理结果对比图。

此处采用的传统stap方法为efa方法，相比于fa方法，它在时域使用了相邻的三个多普勒通道进行空时联合处理，由于增加了时域自由度，有助于改善杂波抑制性能，也能更好地体现本发明所提方法的优势。

参照图3，为某远程距离门内对原始回波数据与本发明空时重构数据作stap杂波抑制后的平均杂波剩余功率对比曲线。图中的纵坐标表示功率的大小，单位为分贝(db)，横坐标为多普勒通道，共64个。图例中的原始数据即为运用stap中的efa方法对原始回波数据作杂波抑制处理，在图中用虚线表示；图例中的空时重构表示本发明中的基于杂波空时等效的三维异构阵空时重构方法，它运用stap中的efa方法对空时重构之后的数据进行杂波抑制处理，在图中用实线表示。从图3可以看出，采用本发明中的空时重构方法经过stap处理后，平均杂波剩余功率更低，取得了优于传统stap方法的杂波抑制效果。

参照图4，为对原始回波数据与本发明空时重构数据作stap杂波抑制后的改善因子对比曲线。图中的纵坐标表示改善因子的大小，单位为分贝(db)，横坐标为多普勒通道，共64个。图例中的原始数据即为运用stap中的efa方法对原始回波数据作杂波抑制处理后的改善因子，在图中用虚线表示；图例中的空时重构表示本发明中的基于杂波空时等效的三维异构阵空时重构方法，它运用stap中的efa方法对空时重构之后的数据进行杂波抑制处理后的改善因子，在图中用实线表示。由wardj在其文献中指出，为使因估计不准确而带来的性能损失在3db以内，要求样本数目至少为协方差矩阵阶数(或自由度)的两倍，本发明所用的独立同分布样本数目满足样本条件。从图4可以看出，采用本发明中的空时重构方法经过stap处理后，相较于传统滤波方法改善了3.1db。

观察图3和图4可以看出，当平台速度满足dpca条件时，将原始数据进行空时重构处理有很好的杂波对消效果，较传统滤波处理改善了杂波旁瓣水平，在主杂波区也有较好的抑制性能。

参照图5，为主杂波区附近的第30号多普勒通道，对原始回波数据与本发明空时重构数据作stap杂波抑制后的改善因子随dpca比例变化曲线。图中的纵坐标表示本发明空时重构数据与原始回波数据分别作stap杂波抑制后的改善因子差值，单位为分贝(db)，横坐标为dpca比例，即实际速度与理想速度之比，比例范围是0.4-1.4。从图5可以看出，在所有比例范围内，两者差值均大于0，这表明即使平台速度偏离了理想的dpca条件，本发明所用方法相比于传统滤波方法仍然有更优的杂波抑制效果。

综上，本发明提出的一种基于杂波空时等效的三维异构阵空时重构方法，主要解决三维异构阵列的体阵列结构带来的接收方向图时的旁瓣性能不稳定导致的杂波抑制性能下降的问题。本发明利用杂波的空时等效特性，当载机速度与脉冲重复频率满足dpca条件时，对空时数据进行重排、截断处理，以满足所有空间位置的相位一致性，达到更好的杂波对消效果。当载机速度不稳定时，本发明方法的杂波抑制性能仍然优于传统滤波方法。因此更提升了本发明方法的应用价值。

本领域普通技术人员可以理解：实现上述方法实施例的全部或部分步骤可以通过程序指令相关的硬件来完成，前述的程序可以存储于计算机可读取存储介质中，该程序在执行时，执行包括上述方法实施例的步骤；而前述的存储介质包括：rom、ram、磁碟或者光盘等各种可以存储程序代码的介质。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以所述权利要求的保护范围为准。