一种构建四阵元立体阵列的方法和装置与流程
本发明涉及阵列天线测向技术领域,具体涉及一种构建四阵元立体阵列的方法和装置。
背景技术:
阵列天线测向系统是一种重要的被动式测向装备,相对于主动工作的雷达系统,除了具有抗截获、抗干扰等优点外,还具有测向精度高、体积重量小、成本低等优点,近年来受到重视,并已多次应用于星载装备。当前常用的测向阵列天线多为平面阵,即多个阵元处于同一平面。在应用过程中,此类平面阵在阵面法向区域(通常为卫星星下点位置)往往可以得到比较理想的测向精度,但在偏离阵面法向方位较远的区域(通常为较小俯仰角区域)测向精度显著下降。然而,在一些特定场景中,除希望阵面法向位置具有较高测向精度外,在偏离法向方位较远的区域仍希望具有较高的测向精度以满足应用需求。
在辐射源波达方向确定的情况下,为了满足在较小俯仰角区域测向精度的需求,通常的做法有阵面偏置、加大阵元尺寸、加大基线长度等。其中,阵面偏置就是通过将阵面的安装平面旋转一定角度以满足应用需求,但这种做法是以牺牲原阵面法向区域测向精度为代价的。加大阵元的本质是通过提升接收信号的信噪比,改善相位差测向精度以提升各区域的测向精度,但对于一些低频段的测向阵存在阵元尺寸原本就较大的问题,进一步加大阵元尺寸将会给阵元的安装、布局带来更大的压力。加大基线长度也将有助于各区域测向精度的提升,但无疑会带来测向模糊的问题。
另外,目前分时测量相位差的方法虽然能够节约系统的计算资源,但是无法实时测向导致测向精度并不高。
技术实现要素:
本发明提供了一种构建四阵元立体阵列的方法和装置,以解决在辐射源波达方向确定的情况下,现有的阵列天线测向系统中较小俯仰角区域的测向精度低以及分时测量相位差无法实时测向导致测向精度并不高问题。
根据本发明的一个方面,提供了一种构建四阵元立体阵列的方法,该方法包括:将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,其中,第一阵元为所述三维直角坐标系的原点;
基于所述初步的四阵元立体阵列同步计算其他三个阵元相对于所述第一阵元的相位差;
根据计算得到的所述其他三个阵元相对于所述第一阵元的相位差构建测向模型;
利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;
选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列。
根据本发明的另一个方面,提供了一种构建四阵元立体阵列的装置,所述装置包括:
立体阵列初步构建单元,用于将传统三阵元平面阵任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,其中,第一阵元为所述三维直角坐标系的原点;
相位差计算单元,用于基于所述初步的四阵元立体阵列同步计算其他三个阵元相对于所述第一阵元的相位差;
测向模型构建单元,用于根据计算得到的所述其他三个阵元相对于所述第一阵元的相位差构建测向模型;
测向误差计算单元,用于利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;
立体阵列最终构建单元,用于选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列。
本发明的有益效果是:本发明的技术方案,通过将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,基于该初步的四阵元立体阵列同步计算其他三个阵元相对于第一阵元的相位差,根据计算得到的相位差构建测向模型,并利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;然后通过选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列,在辐射源波达方向确定的情况下,使用本发明最终构建的四阵元立体阵列,既可以保证在较大仰角区域测向精度,也能够提升在较小俯仰角区域的测向精度,满足待测波方向在期望俯仰角区域的测向精度。另外,本发明采用同步计算阵元间的相位差,相比于分时计算阵元间的相位差的方式,提高了测向精度。
附图说明
图1是本发明一个实施例的一种构建四阵元立体阵列的方法的流程图;
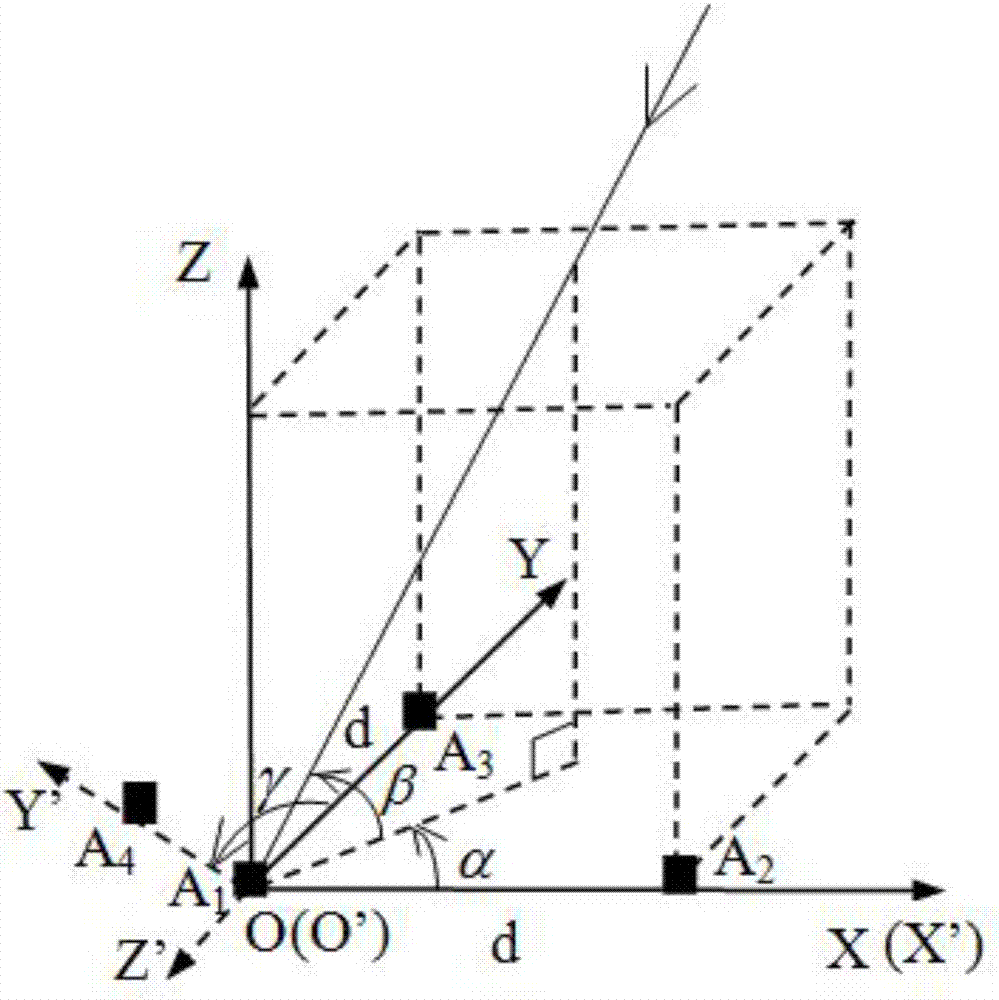
图2是本发明一个实施例的一种四阵元立体直角阵坐标系的示意图;
图3是本发明一个实施例的一种构建四阵元立体阵列的装置的结构示意图;
图4是本发明一个实施例的当γ=45°时,四阵元立体直角阵的测向精度等高线的示意图;
图5是本发明一个实施例的当γ=60°时,四阵元立体直角阵的测向精度等高线的示意图;
图6是本发明一个实施例的当γ=120°时,四阵元立体直角阵的测向精度等高线的示意图;
图7是本发明一个实施例的当γ=135°时,四阵元立体直角阵的测向精度等高线的示意图;
图8是本发明一个实施例的同步测量相位差的三阵元平面l型直角阵的测向精度等高线的示意图;
图9是本发明一个实施例的同步测量相位差的四阵元立体直角阵(γ=120°)与三阵元平面l型直角阵测向精度比的等高线的示意图;
图10是本发明一个实施例的分时测量相位差的四阵元立体直角阵(γ=120°)与三阵元平面l型直角阵测向精度比的等高线的示意图。
具体实施方式
本发明的设计构思是:在不降低平面阵大仰角区域测向精度的情况下,提升了期望较小俯仰角区域的测向精度,将传统三阵元平面阵所在的三维直角坐标系旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列;基于初步的四阵元立体阵列同步计算其他三个阵元相对于同一阵元的相位差;根据计算得到的三个相位差构建测向模型;利用测向模型计算待测波方向的估计值与实际值之间的测向误差;选取若干不同旋转角度的第四阵元,根据测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据最佳旋转角度构建最终的四阵元立体阵列。
实施例一
图1是本发明一个实施例的一种构建四阵元立体阵列的方法的流程图,如图1所示,
在步骤s110中,将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,其中,第一阵元为所述三维直角坐标系的原点。
在步骤s120中,基于所述初步的四阵元立体阵列同步计算其他三个阵元相对于所述第一阵元的相位差。
在步骤s130中,根据计算得到的所述其他三个阵元相对于所述第一阵元的相位差构建测向模型。
在步骤s140中,利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差。
在步骤s150中,选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列。
由此可知,本发明的技术方案,通过将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,基于该初步的四阵元立体阵列同步计算其他三个阵元相对于第一阵元的相位差,根据计算得到的相位差构建测向模型,并利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;然后通过选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列,使用本发明最终构建的四阵元立体阵列,既可以保证在较大仰角区域测向精度,也能够提升在较小俯仰角区域的测向精度,满足待测波方向在期望俯仰角区域的测向精度。另外,本发明采用同步计算阵元间的相位差,相比于分时计算阵元间的相位差的方式,提高了测向精度。
为了使本发明的方案更加清晰,下面举一个具体的例子进行解释说明。在本发明的一个实施例中,
(一)创建坐标系
图2是本发明一个实施例的一种四阵元立体直角阵坐标系的示意图,如图2所示,oxyz是传统平面l型三阵元直角阵的坐标系,其中直角阵的三个阵元分别布置于坐标原点o(a1),x轴(a2),y轴(a3),阵列基线长度为d(需要说明的是,本实施例中阵列基线长度指的是其他三阵元相对于第一阵元的距离)。在此基础上,将坐标系oxyz绕其x轴正向旋转角度γ则得到另一坐标系o’x’y’z’,在y’轴上添加所述第四阵元a4,阵列基线长度同样为d。在坐标系oxyz内,假设辐射源波达方向与oxy平面夹角为β,记为俯仰角。此外,假设辐射源波达方向矢量在oxy平面的投影与ox夹角为α,记为方位角。为简便计,将辐射源波达方向统一记为(α,β)。
(二)相位差计算
在图2构建的立体阵坐标系中,以阵元a1为基准,通常考虑基线长度小于半波长的情形(需要说明的是,若基线长度大于半波长,那么将导致测向模糊。),则此时阵元a2与a1的相位差φ21为:
(公式1)中λ是待测波方向的波长,d为阵列基线长度,δφ21为阵元a2与a1通道之间的相位差测量误差之差。另一方面,阵元a3与a1的相位差φ31为:
(公式2)中,δφ31为阵元a3与a1通道之间的相位差测量误差之差。此外,阵元a4与a1的相位差φ41为:
(公式3)中,δφ41为阵元a4与a1通道之间的相位差测量误差之差。
将(公式1)—(公式3)用矩阵表示为:
(公式4)中,
(三)构建测向模型
对相位差测量值矩阵(公式4)进行最小二乘法处理,得到测向模型为:
需要说明的是,(公式5)中,t表示矩阵的转置,σ为正定矩阵,θ是待测波方向矢量,且θ=(α,β);
(四)测向误差推导
为估计经由(公式5)估计得到的辐射源波达方向
设
由于
对于(公式8)等式左侧,直接计算可得:
因此,有:
(公式10)中,
对于(公式8)等式左侧,直接计算可得:
另外,(公式10)中直接计算有
(公式12),cov(δθ)指δθ的协方差矩阵。
在本发明的一个实施例中,同步计算其他三个阵元相对于第一阵元的相位差指的是在某一时刻(或者某一时间段)同时测量a2-a1,a3-a1,a4-a1三组基线中一组的相位差,换句话说,就是计算机编程语言中的并行计算a2-a1,a3-a1,a4-a1三组相位差。同步计算阵元间的相位差,相比于分时计算阵元间的相位差的方式,提高了测向精度。在同步测量相位差的过程中,假设
(公式13)中,
(公式14)中,
记
(公式15)中,
根据式(公式15)的结果,计算所述待测波方向的估计值和实际值之间的夹角方差为
其中
(五)四阵元立体测向阵列构建
根据(公式16)可知,给定旋转角γ,在不同的方位角α、俯仰角β,均可计算得到测向误差
根据实际的应用需求,选取若干不同旋转角度的第四阵元,根据所述测向误差(公式16)分别对应计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建四阵元立体阵列。也就是说,可通过选取满足应用需求的阵元a4的多个旋转γ角,观察在感兴趣的区域其测向精度,确定最终的立体阵构型。
实施例二
图3是本发明一个实施例的一种构建四阵元立体阵列的装置的结构示意图,如图3所示,所述装置包括:
立体阵列初步构建单元210,用于将传统三阵元平面阵任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,其中,第一阵元为所述三维直角坐标系的原点;
相位差计算单元220,用于基于所述初步的四阵元立体阵列同步计算其他三个阵元相对于所述第一阵元的相位差。
测向模型构建单元230,用于根据计算得到的所述其他三个阵元相对于所述第一阵元的相位差构建测向模型;
测向误差计算单元240,用于利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;
立体阵列最终构建单元250,用于选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列。
由此可知,本发明的技术方案,通过将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,基于该初步的四阵元立体阵列同步计算其他三个阵元相对于第一阵元的相位差,根据计算得到的相位差构建测向模型,并利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;然后通过选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列,在辐射源波达方向确定的情况下,使用本发明最终构建的四阵元立体阵列,既可以保证在较大仰角区域测向精度,也能够提升在较小俯仰角区域的测向精度,满足待测波方向在期望俯仰角区域的测向精度。另外,本发明采用同步计算阵元间的相位差,相比于分时计算阵元间的相位差的方式,提高了测向精度。
在本发明的一个实施例中,所述立体阵列初步构建单元210,用于将将传统三阵元平面阵所在的三维直角坐标系oxyz绕x轴正向旋转一角度,得到三维直角坐标系o’x’y’z’,在y’轴上添加所述第四阵元,且第二阵元位于x轴,第三阵元位于y轴,所述第二阵元、第三阵元和第四阵元分别相对于所述第一阵元的基线长度相等。
在本发明的一个实施例中,所述相位差计算单元220,用于根据公式
根据公式
根据公式
其中,d是所述第二阵元、第三阵元和第四阵元分别相对于所述第一阵元的基线长度,λ是待测波方向的波长,β是待测波方向的俯仰角,α是待测波方向的方位角,γ是所述第四阵元相对于所述三维直角坐标系的旋转角度,δφ21是所述第二阵元与所述第一阵元之间的相位差测量误差之差,δφ31是所述第三阵元与所述第一阵元之间的相位差测量误差之差,δφ41是所述第四阵元与所述第一阵元之间的相位差测量误差之差。
在本发明的一个实施例中,所述测向模型构建单元230,用于根据公式
对所述相位差测量值矩阵进行最小二乘法处理,得到测向模型
其中,t表示矩阵的转置,σ为正定矩阵,θ是待测波方向矢量,且θ=(α,β)t;
在本发明的一个实施例中,所述测向误差计算单元240,用于根据所述测向模型和所述相位差测量误差矩阵计算待测波方向的估计值和理论值之间的夹角;
计算所述待测波方向的估计值和理论值之间的夹角的协方差矩阵,得到待测波方向的方位角测量误差方差
且
根据公式
b11=cβ(-5sα-cα-cαcγ),b12=cβ(sα+5cα-cαcγ),b13=cβ(sα-cα+5cαcγ),
b21=sβ(-5cα+sα+sαcγ)-cβsγ,b22=sβ(cα-5sα+sαcγ)-cβsγ,
b23=sβ(cα+sα-5sαcγ)+5cβsγ,
cα=cosα0,cγ=cosγ0,sα=sinα0,sγ=sinγ0,
α0是待测波方向方位角的理论值,β0是待测波方向俯仰角的理论值,将
需要说明的是,图3所示的装置的工作过程与图1所示的方法的各实施例的实现步骤对应相同,相同的部分不再赘述。
实施例三
在本实施例中,以一个低轨卫星四阵元立体直角阵的实施案例以演示其应用步骤及效果。在本实施案例中,采用相位差同步测量体制,也就是采用相位差同步接收处理体制,且各阵元相位差测量误差均为10°。在实际应用中,除对关系星下点附近(即俯仰角90°附近)的测向精度要求很高外,对于俯仰角35°至50°区域的测向精度也有一定要求。图4是本发明一个实施例的当γ=45°时,四阵元立体直角阵的测向精度等高线的示意图;图5是本发明一个实施例的当γ=60°时,四阵元立体直角阵的测向精度等高线的示意图;图6是本发明一个实施例的当γ=120°时,四阵元立体直角阵的测向精度等高线的示意图;图7是本发明一个实施例的当γ=135°时,四阵元立体直角阵的测向精度等高线的示意图。
如图4-7所示,当γ=45°时,较小仰角区域35°至50°区域的测向精度为(4.6,5.4);当γ=60°时,较小仰角区域35°至50°区域的测向精度为(4.2,5);当γ=120°时,较小仰角区域35°至50°区域的测向精度为(3.5,6);当γ=135°时,较小仰角区域35°至50°区域的测向精度为(3.5,6.5),当旋转角γ=120°时,在较小仰角区域35°至50°区域的测向精度最高,因此,当对较小仰角区域35°至50°区域的测向精度要求较高时,选取旋转角γ=120°构建四阵元立体阵。
本例中,作为比较,还考虑了同等相位差测量误差情况下传统的三阵元l型平面阵。图8是本发明一个实施例的同步测量相位差的三阵元平面l型直角阵的测向精度等高线的示意图,需要说明的是,图8中的阵元平面l型直角阵指的就是图2中a1、a2、a3阵元构成的测向阵。图9是本发明一个实施例的同步测量相位差的四阵元立体直角阵(γ=120°)与三阵元平面l型直角阵测向精度比的等高线的示意图;图10是本发明一个实施例的分时测量相位差的四阵元立体直角阵(γ=120°)与三阵元平面l型直角阵测向精度比的等高线的示意图。
对比分析图8、图9和图10的结果可见,本发明的技术方案设计的四阵元立体直角阵在俯仰角较小时优势显著,其各区域测向精度不仅优于传统的三阵元l型平面阵,且优于采用分时接收处理体制的相同构型的直角阵。需要说明的是图4至图10中的数字代表精确度。
综上所述,本发明的技术方案,通过将传统三阵元平面阵所在的三维直角坐标系任意旋转一角度,添加一个非共面的第四阵元,构建初步的四阵元立体阵列,基于该初步的四阵元立体阵列同步计算其他三个阵元相对于第一阵元的相位差,根据计算得到的相位差构建测向模型,并利用所述测向模型计算待测波方向的估计值与实际值之间的测向误差;然后通过选取若干不同旋转角度的第四阵元,根据所述测向误差分别计算待测波方向在期望俯仰角区域的测向精度,将计算得到的最高测向精度对应的旋转角度确定为最佳旋转角度,并根据所述最佳旋转角度构建最终的四阵元立体阵列,在辐射源波达方向确定的情况下,使用本发明最终构建的四阵元立体阵列,既可以保证在较大仰角区域测向精度,也能够提升在较小俯仰角区域的测向精度,满足待测波方向在期望俯仰角区域的测向精度。另外,本发明采用同步计算阵元间的相位差,相比于分时计算阵元间的相位差的方式,提高了测向精度。
以上仅是本发明的较佳实施例而已,并非用于限定本发明的保护范围。凡在本发明的精神和原则之内所作的任何修改、等同替换、改进等,均包含在本发明的保护范围内。
- 还没有人留言评论。精彩留言会获得点赞!