透射反射模态融合的超声层析成像方法与流程

本发明属于超声层析成像技术领域，涉及实现一种利用透射反射模态融合的超声层析成像方法，用于实现被测物场两相介质分布的重建和可视化表征。

背景技术：

超声层析成像技术(ultrasonictomography,ut)是一种结构性成像技术，其通过在被测场域外布置超声传感器阵列并施加一定的激励以得到边界电压测量数据，以此来重建被测场域内部的折射系数、衰减系数或声阻抗分布情况。相比软场成像技术例如电阻抗层析成像(electricalimpedancetomography,eit)和电磁层析成像(magneticimpedancetomography,mit)，ut具有非侵入、分辨率高的优点，相比精度较高的硬场成像技术如x射线层析成像(x-raycomputedtomography,x-ct)及光学层析成像方法(opticalcoherencetomography,oct)，ut使用安全、结构简单、可以实现实时成像。此外ut还有着非接触、方向性好、成本低等优势，是一种较为理想的过程可视化检测监视手段。ut作为一种层析成像技术手段，在多相流可视化检测、化工石油输送、航空发动机探查以及生物医学诊断中均有广泛的应用。

完整的ut系统主要包含三个部分：传感器阵列设计与换能器安装；信号激励、采集系统；超声成像重建算法。其中超声成像算法通过对从采集系统得到的换能器接收信号进行处理，通过解调提取测量幅值或渡越时间，得到某个确定激励下的全部换能器的有效测量数据，进一步通过图像重建方法得到被测物场两相介质分布的合理估计。目前，超声成像重建算法主要存在成像分辨率低、成像精度差、图像伪影严重等三个方面的问题。此外，作为一种主要利用硬场特性的成像方法，超声成像方法严重依赖于场域边界换能器的数量，其逆问题求解具有严重的病态性(对测量值得微小扰动会导致重建结果的大幅度变化)和欠定性(所需求解的方程数远小于未知量的数目，方程有无穷多解)。为克服这个问题，学者们提出了许多图像重建算法，超声层析成像图像重建方法根据其模态的不同主要分为透射法和反射法两类，其中透射法通过记录相对于发射探头的超声换能器接收到的电压信号实现渡越时间、衰减幅值的提取，进而实现被测物场两相介质分布的重建，反射法通过记录发射探头接收到的反射声波信号，通过提取对应渡越时间确定两相介质中离散相边界位置，通过提取渡越时间对应信号幅值确定边界声阻抗差异。在过去的研究中，透射法方面，典型的图像重建方法有徐立军等人1998年在《仪器仪表学报》(chinesejournalofscientificinstrument)第17卷，1-7页，发表的题为《气液两相泡状流体监测用超声层析成像系统的研究》(investigationofultrasoundtomographysystemusedformonitoringbubblygas/liquidtwo-phasefluid)的文章中提到的二值反投影方法、rahim等人在《传感器与执行器》(sensorsandactuators)第135卷，337-345页发表的题为《超声对液体、气体的非侵入性成像》(non-invasiveimagingofliquid/gasflowusingultrasonictransmissionmodetomography)的文章中提到的采用r-l函数的线性滤波反投影方法、gordon等人在《理论生物学杂志》(journaloftheoreticalbiology)第29卷，第3期，471-481页发表的题为《用于三维电子显微镜和x射线ct的代数重建技术》(algebraicreconstructiontechniques(art)forthree-dimensionalelectronmicroscopyandx-rayphotography)的文章中提出的代数重建方法、苏邦良等人在《化学工程期刊》(chemicalengineeringjournal)第77卷，37-41页发表的题为《同步迭代重建技术在电容层析成像中的应用》(theuseofsimultaneousiterativereconstructiontechniqueforelectricalcapacitancetomography)的文章中提出的同步迭代重建方法、anderson等人在《超声成像》(ultrasoundimaging)第6卷，81-94页发表的题为《同步代数重建技术(sart)：art算法更优越的实现》(simultaneousalgebraicreconstructiontechnique(sart):asuperiorimplementationoftheartalgorithm)的文章中提出的同步代数重建方法等；在反射法方面，典型的图像重建算法有2013年徐春广等人在《仪器仪表与传感器》(instrumentationtechniqueandsensor)2013-04期中发表的题为《基于vc++的超声探伤仪发射端信号测量与处理系统》的文章中提出的反射式超声椭圆成像算法、2017年langener等人在《流动测量与设备》(flowmeasurementandinstrumentation)第53卷，107-115页发表的题为《一种基于超声反射重建技术的实时超声过程层析成像系统》(areal-timeultrasoundprocesstomographysystemusingareflectionmodereconstructiontechnique)的文章中体出的基于路径追踪的超声反射图像重建算法。

上述超声层析成像图像重建方法中，往往采用透射法或反射法单独进行图像重建，透射法和反射法对不同位置及不同声阻抗比的介质有较为互补的成像效果，如反射法对靠近场域边界的离散相介质可以实现较好的重建，透射法对靠近场域中央的离散相介质可以实现较好的重建，但两种方法单独使用的时候对不同位置的成像效果差别较大，无法做到对各个位置的离散相介质分布进行快速、准确的可视化表征。此外，在超声成像图像重建算法及其改进方法中，探头数量的多少对重建图像精度及重建图像分辨率有至关重要的影响，即超声成像图像重建方法与探头间的有效路径数目紧密相关：投影路径越多，成像精度越高，伪影越少。但在upt实际应用过程中，受限于场域尺寸及信号激励幅值限制，场域边界的探头数不能无限增加；另一方面，超声作为机械波在场域内的传播需要一定的渡越时间，换能器数目过多无法满足可视化监测的实时性要求。单独使用透射法或反射法进行图像重建均仅能利用超声信号中包含的部分信息，无法在保证较快的数据成像速度前提下实现较高精度的图像重建。因此需要一种在低投影数量下有效利用透射反射多模态信息的图像重建算法，以期在保证实时性图像重建速度的同时实现叫高精度的重建。

技术实现要素：

本发明的目的在于提出一种利用透射反射模态融合的超声层析成像方法，用于实现被测物场两相介质分布的重建和可视化表征。通过数字正交乘法解调同时获取反射渡越时间及透射幅值衰减信息。基于解调信息，搭建反射边界约束方程并提出基于滤波反投影的联合约束图像重建方法，解决了透射及反射图像重建算法分别在某些情况下出现成像失败的问题，扩展了滤波反投影代数重建方法的应用，提高超声过程层析成像逆问题的求解精度和图像重建质量。技术方案如下：

一种透射反射模态融合的超声层析成像方法，用于实现被测物场两相介质分布的重建和可视化表征，包含以下步骤：

(1)在被测场域外表面均匀的布置n个超声换能器，并使用四周期脉冲正弦波电压对发射探头进行激励，场域边界上的所有超声换能器均用于接收超声信号，采用循环激励的策略，场域内边界的每个超声换能器均分别用来进行激励，对于n个超声换能器构成的传感器阵列，共接收n×n个时变超声信号；

(2)采用数字正交乘法解调对所获得的超声时变信号解调，得到正交解调结果，即幅值a和信号滞后的相位

(3)根据正交解调采集信号每一点的幅值和相位信息进行每一点的幅值大小比值，将前一时刻的数据点与下一时刻的数据点进行比较，最终保存的值为接收脉冲信号的最大幅值，停止刷新后，累加器的计数值为测量脉冲信号的最大幅值，最大幅值即为解调得到的边界电压测量值，其对应的时间即为解调得到的渡越时间；

(4)计算离散相介质边界点距超声换能器的距离并构建超声反射约束方程，方法如下：

[1]根据对每个超声换能器自发自收超声信号进行解调得到的渡越时间，计算内含离散相介质边界点与超声换能器探头的轴线距离：

其中，dt-r表示离散相介质边界点与超声换能器探头的轴线距离，toft-r表示对应离散相介质边界点距离的渡越时间，cw表示被测场域内连续相介质的声速；

[2]根据场域内每个换能器对应的离散相介质边界距离，构建超声反射约束方程，其计算方式表示为：

h(α)＝[α(p1)-a1·p1,α(p2)-a2·p2,…,α(pn)-an·pn]^t＝0

其中，α(·)表示衰减系数，p2表示被测场域内的第二个像素，pn表示被测场域内的第n个像素，a1表示第一个像素的反射权系数值，以此类推，将离散相介质边界内部像素的反射权系数值取值为离散相介质边界外部像素反射权系数值的整数倍，一般取值大于1000；

(5)计算透射模态下超声换能器接收信号的幅值衰减，方法如下：

[1]获取重建所需的投影衰减测量值v(ti,rj)，其计算方式表示为：

其中，fc是激励信号的中心频率，as为空场下的边界电压测量值，ar为存在离散相介质情况下的边界电压测量值，(ti,rj)表示第i个换能器发射、第j个换能器接收对应的投影衰减值，ln表示对数符号；

[2]构建系数矩阵，即在不含离散相介质空场内根据机里探头和接收探头的相对位置计算器连线穿过场域内像素的情况，其计算公式为：

其中，表示坐标为(x,y)的像素点对应投影路径的系数矩阵取值，(ti,rj)表示第i个换能器发射、第j个换能器接收对应系数矩阵中的行，m表示投影路径与像素的重叠面积，l表示像素的边长；

[3]计算滤波系数矩阵其计算方式表示为：

其中，pm表示系数矩阵中的最大值，num表示换能器数目，∑表示求和；

(6)计算透射反射双模态图像重建结果g(x,y)：

本发明中所提出的方法，可以在低投影数量下解决透射及反射图像重建算法分别在某些情况下出现成像失败的问题，扩展滤波反投影代数重建方法的应用，有效提高超声过程层析成像逆问题的求解精度和图像重建质量。本发明实现了测量中对透射及反射模态信息的提取、解耦、及联合利用，在提升图像重建精度的同时显著降低了成像伪影。通过搭建反射边界约束方程并使用基于滤波反投影的联合约束图像重建方法，扩展了滤波反投影代数重建方法的应用，提高超声过程层析成像逆问题的求解精度和图像重建质量。

附图说明

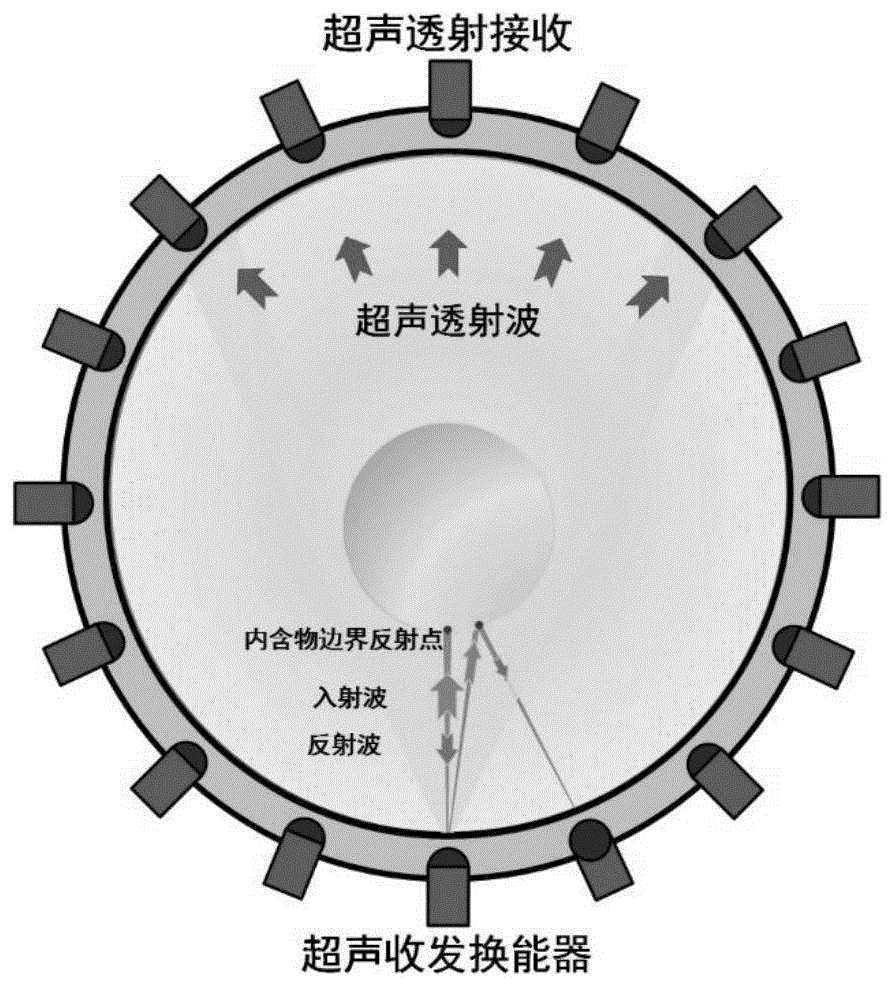
图1为本发明中透射反射双模态信息采集示意图；

图2为本发明中采用的数字正交乘法解调流程示意图；

图3为本发明中针对离散相介质分布(distribution)的实验图像重建结果，并分别给出了相应的透射法成像结果(t-mode)、反射法成像结果(r-mode)、本算法所提出双模态成像结果(dual-mode)，；

图4为针对本发明的十组仿真模型不同成像结果的相对误差和图像相关系数对比。

具体实施方式

结合附图和实施例对本发明的基于非均匀形状约束的像素值域滤波超声成像算法加以说明。

本发明的透射反射双模态融合的工业过程超声层析成像图像重建方法，实施例中针对工业输油管道中油水两相流的成像这一ut技术的常见应用形式，使用基于投影路径长度的系数矩阵构建方法表征油水两相流超声可视化检测的正问题模型，同时将图像重建逆问题的求解过程分解为数字正交乘法解调、反射约束方程构建、透射系数矩阵及滤波矩阵计算、联合图像重建四个部分。以达到透射反射双模态信息有效提取、解耦、联合图像重建的目的，以提高低投影数量下的对离散相介质位置、轮廓的准确描述。

如图1所示，为本发明的基于非均匀形状约束的像素值域滤波超声成像算法完整流程图。算法主要分为基于投影路径长度的系数矩阵构建、同步迭代重建与非均匀形状约束的像素值域滤波三部分，系数矩阵在已知场域分布、探头尺寸和探头布置位置的基础上，由数值计算方法获得。

图2是数字正交乘法解调流程示意图。经过数字模拟转换控制模块之后，测量信号被转换成为二进制补码形式的数字信号，通过相敏解调数字化的测量信号，以获得超声回波信号的幅值和渡越时间信息。模拟乘法解调和数字乘法解调是相敏解调中最常用的方法，其中模拟解调需要低通滤波器。由于模拟解调的响应时间较长，不利于提高系统的实时性能，因此采用数字正交乘法解调并在fpga内部实现。数字解调可以在单个信号周期中获得信号解调的结果。当激励周期开始时，开关切换模块提供触发信号，控制着fpga内部的数字解调模块的开始与结束。upt系统16通道的数据解调方式为并行解调。同时，系统中的每个通道都采用组合解调模式，在分别对幅值解调数据和渡越时间解调数据进行编号和打包之后，根据通道序列将它们两者依次发送到异步fifo。

图3中分别给出了模型1-模型10对应的成像结果。可以看出，传统透射模式或反射模式均无法有效实现不同位置、不同数目、不同尺寸离散相介质的有效重建。本发明所提出的算法能够较准确地重建出离散相介质的准确位置和完整形状。重建结果中，离散相介质边界清晰，图像无过多伪影及噪声，图像分辨率、成像精度均有明显提高

图4中分别给出了传统超声层析成像图像重建算法的成像结果与本算法的成像结果重建指标对比，重建指标包括相对误差(re)和图像相关系数(cc)两种，其计算方法表示为：

其中，σ表示重建的像素单元电导率分布，σ^*表示真实情况下的电导率分布，σj和σj^*表示第j个像素单元重建的和真实的电导率分布，和表示重建的和真实的电导率分布的平均值。

本算法实施例包括如下具体步骤：

(1)：在被测场域外表面均匀的布置n个超声换能器，并使用四周期脉冲正弦波电压对发射探头进行激励，场域边界上的所有超声换能器均用于接收超声信号。采用循环激励的策略，场域内边界的每个超声换能器均分别用来进行激励，对于n个超声换能器构成的传感器阵列，共接收n×n个时变超声信号。

(2)：采用数字正交乘法解调对所获得的超声时变信号解调，解调过程在配套测量系统中通过逻辑门电路阵列实现。

a.设模拟-数字转换器提供的采样率为fs，对超声换能器接收到的正弦交流测量信号进行采样，得到的数字化的测量信号表达式，其计算方式表示为：

其中，k表示采样点序号，y(k)表示第k个采样点的值，sin表示正弦函数，π表示圆周率，f表示激励信号频率，表示信号滞后的相位，a表示数字化测量信号的幅值，m表示第k个采样点序号表示的测量时间。

b.将正弦和余弦标准正交参考信号分别与数字化测量信号相乘，即可得到两个相互正交的乘积信号，其计算方式表示为：

其中，n为一个完整信号周期内采样点的总个数，cos表示余弦函数，pi(k)和pq(k)表示两个相互正交的乘积信号。

c.将两个相互正交的乘积信号按整数周期累加，得到正交解调结果，其计算方式表示为：

d.根据正交解调采集信号每一点的幅值和相位信息进行没一点的幅值大小比值，将前一时刻的数据点与下一时刻的数据点进行比较，最终保存的值为接收脉冲信号的最大幅值。停止刷新后，累加器的计数值为测量脉冲信号的最大幅值。

(3)：基于步骤二的解调结果，计算离散相介质边界点距超声换能器的距离并构建超声反射约束方程。

a.根据对每个超声换能器自发自收超声信号进行解调得到的渡越时间，计算离散相介质边界点与超声换能器探头的轴线距离，其计算方式表示为：

其中，dt-r表示离散相介质边界点与超声换能器探头的轴线距离，toft-r表示对应离散相介质边界点距离的渡越时间，cw表示被测场域内连续相介质的声速。

b.根据场域内每个换能器对应的离散相介质边界距离，构建超声反射约束方程，其计算方式表示为：

h(α)＝[α(p1)-a1·p1,α(p2)-a2·p2,…,α(pn)-an·pn]^t＝0

其中，α(·)表示衰减系数，p2表示被测场域内的第二个像素，pn表示被测场域内的第n个像素，a1表示第一个像素的反射权系数值，以此类推。将离散相介质边界内部像素的反射权系数值取值为离散相介质边界外部像素反射权系数值的1000倍。

(4)：基于步骤二的解调结果，计算透射模态下超声换能器接收信号的幅值衰减。

a.获取重建所需的投影衰减测量值v(ti,rj)，其计算方式表示为：

其中，fc是激励信号的中心频率，as为空场下的边界电压测量值，ar为存在离散相介质情况下的边界电压测量值，(ti,rj)表示第i个换能器发射、第j个换能器接收对应的投影衰减值，ln表示对数符号。

b.构建系数矩阵，即在不含离散相介质空场内根据机里探头和接收探头的相对位置计算器连线穿过场域内像素的情况，其计算公式为：

其中，表示坐标为(x,y)的像素点对应投影路径的系数矩阵取值，(ti,rj)表示第i个换能器发射、第j个换能器接收对应系数矩阵中的行。

c.计算滤波系数矩阵其计算方式表示为：

其中，pm表示系数矩阵中的最大值，num表示换能器数目，∑表示求和。

(5)：基于步骤二～步骤四种的计算结果，计算透射反射双模态图像重建结果g(x,y)，其计算方式表示为：