考虑太阳翼辐射损伤的全电推航天器轨道转移优化方法与流程

背景技术：
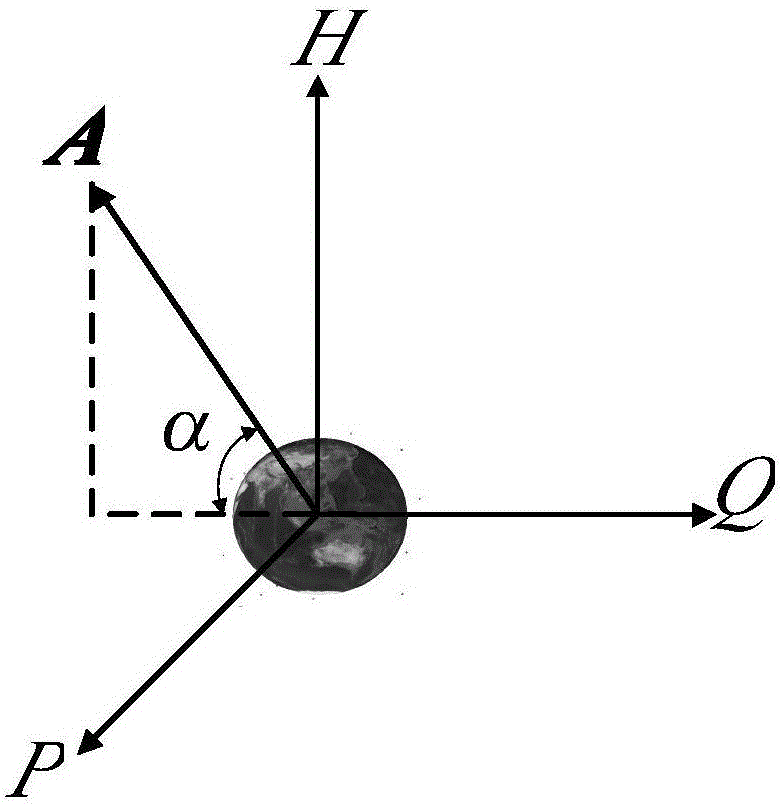
：电推进系统具有高效率、高比冲的特点，可以大幅提高航天器平台有效载荷承载能力、延长在轨寿命并降低发射成本，因此我国已经开始全电推卫星平台的关键技术研究及平台开发工作。全电推卫星平台能够实现星箭分离后的卫星轨道转移轨道变轨、卫星入轨后的轨道位置保持、动量卸载以及离轨等任务，可取消复杂的双组元化学推进系统，从而有效降低综合研制费用，显著提升卫星平台的市场竞争力。美国于2015年成功发射了世界上首个电推进平台——波音公司的BSS-702SP电推进通信卫星平台。BSS-702SP平台采用四台XIPS-25离子推力器，单台推力器推力最大可达到165mN，比冲3500s，功率4.5kW，变轨时需要两台离子推力器同时工作。采用电推进技术大大减轻卫星的发射质量，因此可采用一箭双星发射，大幅节省发射成本。该平台在不影响卫星通信能力和性能的前提下，发射费用减少了5000～6000万美元。电推进已经成为21世纪的关键航天技术，能够承载更多有效载荷实现航天飞行更好的推进效果。然而，由于电推进产生的推力很小(一般为几十到几百毫牛)，地球静止轨道(GEO)航天器需要3～8个月的轨道转移时间。时间长变轨会带来以下几个问题：(1)地球辐射带的高能粒子影响太阳翼使得航天器能源供给能力降低，分析结果表明在GTO至GEO转移轨道运行半年的总辐射剂量相当于GEO轨道运行半年总辐射剂量的5倍；(2)安全性降低，航天器频繁穿越静止轨道使得其与已有卫星、碎片等碰撞的几率增加；(3)轨道转移成本增加，长时间的变轨会引起地面测控站费用、入轨晚而产生的其他费用增加。在长时间的变轨过程中，航天器会反复穿越地球辐射带，太阳翼的辐射总剂量会有所增加，导致太阳翼的衰退率增大。因此在地球静止轨道航天器变轨过程中，有效降低太阳翼损伤、提高太阳翼的输出效率对于延长航天器的寿命尤为重要。太阳翼损伤不仅与航天器在辐射带中运行的时间有关，还与所受辐射强度有关，如何在减少轨道转移时间的同时降低太阳翼损伤是电推进航天器发展需要解决的关键问题。本发明提出了一种考虑太阳翼辐射损伤的全电推地球静止轨道转移优化方法，该方法将地球同步转移轨道设计问题转化为考虑转移时间最短与太阳翼功率退化最小的多目标优化问题，并用物理规划方法获取该问题的最优解，最终获得全电推地球静止轨道航天器轨道转移的方案，从而为全电推航天器的方案论证提供参考，并为其控制系统的工程研制提供重要支撑。为了更好的说明本发明的技术方案，下面对应用到的物理规划理论相关数学基础进行具体介绍：物理规划基本理论物理规划方法的核心思想是引入偏好函数，将不同的目标函数转换为量级相同的满意度目标。偏好函数就是让用户决定“多好是好，多坏是坏”的函数，目标函数值和偏好函数值是一一映射的关系，偏好函数值越小说明该目标函数越令人满意。物理规划中的偏好函数可以分为3种类型，即越小越好、越大越好和越趋于某个值越好。每种偏好又分为软、硬(S，H)两种类型。为使物理规划更加方便，利用5个边界值将软偏好分解为6个连续的表示不同满意度的区间：很期望、期望、可接受、不期望、很不期望、不接受。以越小越好类软偏好为例，物理规划分区如图1所示，优化流程如图2所示。定义偏好函数曲线的五个边界值为gi，与之对应的五个偏好函数值为gPi，斜率为Si,i＝1,2...5。其中gi和gP1由用户作为偏好给定，其余根据物理规划理论相关规定进行计算。规定g为目标函数值，gP为与之对应的偏好函数值。规定1区的曲线函数为：在第i(i＝2,3,...,5)区内令:其中，Δxi为第i个偏好区间的长度，为xi在第i个区间的的相对长度。则可得2区至5区的曲线函数的第i个区域为：由上可见，只要求得g1处的斜率就可以确定1区的曲线；只要求得a,b,c,d就可以确定出2至5区的曲线。a,b,c,d由边界点处的函数值及导数值唯一确定，因此，求解曲线的过程就转化为求解各个边界点的gP值，也就是gPi，以及该处的斜率的问题。物理规划曲线的求解过程参照物理规划理论的规定如下所示：(1)用户根据自己的偏好给定5个gi，i＝1,2...5，并设置g1处的gP值gP1为(2)求解各个区域两边界处gPi的差值Δyi，其中：Δyi＝β·nsc·Δyi-1，i＝2,3,...,5。式中nsc是软偏好的个数，β是凸性参数。(3)求解各个区域边界处的gP值gPi，其中：gPi＝gP(i-1)+Δyi，i＝2,3,...,5。(4)求各分区Δx值，其中Δx1没有意义，可以随意赋值，Δxi＝gi-gi-1。(5)求各分区的截率J，其中J1没有意义，可以随意赋值，Ji＝Δyi/Δxi，i＝2,3...5。(6)求各分界点处的斜率S，其中S1＝α·J2，Si＝Smin+α·ΔS,i＝2,3,...,5。式中，Smin＝(4Ji-Si-1)/3，ΔS＝8(Ji-Si-1)/3。由上述过程得到各个边界点的值和斜率后代入式(4)和式(5)就可以求得2-5区域的曲线参数a,b,c,d。左边界：右边界：求得a,b,c,d后就可得到2至5区的曲线函数，由S1等参数可以确定1区的曲线函数。于是可以得到所有目标函数的偏好函数曲线。对于每一组设计变量都可以求得各个目标函数值，将目标函数值带入偏好函数曲线就可以得到对应的偏好函数值，进而得到物理规划总偏好，也就是目标函数，如式(6)所示，其中nsc为软偏好的个数。技术实现要素：本发明针对全电推地球静止轨道航天器轨道转移过程需要较长时间以及穿越地球辐射带造成太阳翼损伤的问题，提出了考虑太阳翼辐射损伤的全电推航天器轨道转移优化方法。该方法的轨道转移策略分为两个阶段，第一阶段，将轨道偏心率消除至0并降低轨道倾角；第二阶段，完成非共面圆轨道之间连续推力转移，使得轨道转移结束时航天器位于地球静止轨道。根据航天器轨道转移过程中的位置参数与运行时长，计算地球辐射带中带电粒子对太阳翼的损伤效应，进而计算太阳翼的功率退化量。在此基础上，建立综合考虑轨道转移时间和太阳翼功率下降系数的多目标物理规划模型并用遗传进行求解，获取最优轨道转移方案。本发明实用性强，为电推进在航天器上的应用提供了有力支持，有利于延长航天器在轨寿命、增加有效载荷，并达到降低成本的目的。为了更好地描述轨道转移涉及的模型，建立了相应的坐标系。其中坐标系RTN原点位于航天器质心，R为轨道径向方向，N为轨道角动量方向，T与R、N垂直且指向运动方向；坐标系PQH原点位于地心，P指向近地点，H指向轨道角动量方向，Q与P、H成右手系；坐标系UVW为原点位于航天器质心，U沿航天器速度方向，V位于轨道面内垂直于速度且指向地心方向，W与U和V垂直且指向轨道面方向。一种考虑太阳翼辐射损伤的全电推航天器轨道转移优化方法，其实现步骤如下：步骤A：确定轨道转移模型初始条件，包括推力T、航天器发射质量m0、比冲Tsp，以及第一阶段轨道转移的初始轨道Kepler根数，包括轨道半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角ω和平近点角M。步骤B：建立轨道转移第一阶段模型。该阶段将轨道偏心率消除至0，同时降低轨道倾角。本发明将电推力器产生的推力作为摄动力处理，建立轨道转移期间的Gauss型轨道摄动方程如式(7)所示，其中a、e、i、Ω、ω、M为轨道根数，f为真近点角，r为轨道半径，u＝ω+f为轨道幅角，p＝a(1-e2)为轨道通径，E为偏近点角,F＝[FR,FT,FN]为推力加速度在轨道坐标系RTN下的分量。此阶段推力位于PQW系的QOW平面内，与-Q所成夹角为α。α的绝对值维持恒定，当轨道幅角u位于90°或270°时，α需要改变正负。采用Runge-Kutta法对建立的Gauss动力学方程进行求解，当轨道偏心率接近于0时，第一阶段轨道转移结束，输出当前轨道的转移时长tf1、轨道倾角i、半长轴a以及航天器质量m0作为第二阶段的输入。步骤C：建立第二阶段轨道转移模型。该阶段完成非共面圆轨道之间的最优连续推力转移，保证轨道转移任务结束时航天器位于地球静止轨道，推力加速度矢量固定在UVW坐标系中的UOW平面内，并与轨道平面保持方位角β。该阶段轨道转移时间tf2计算公式如式(8)所示，其中Δv为第二阶段轨道转移的速度增量。步骤D：输出轨道转移两阶段总时间。基于上述两阶段轨道转移模型，可以得到GTO-GEO转移总时间tf为：tf＝tf1+tf2(9)步骤E：建立太阳翼损伤模型。主要考虑空间质子对太阳翼的位移效应造成的损伤，建立全电推GEO航天器太阳翼损伤模型。质子全向辐射通量ψp是McIlwain坐标L和纬度l的函数，如式(10)所示，其中E为质子能量。式中L＝r/(Rcos2l)，R为地球半径，r为辐射带位置坐标参数，a和b计算公式如式(11)所示，其中a0、a1、a2、a3、b0、b1、b2、b3、b4、b5为常数。于是能量为E的质子产生的位移损伤Dd如式(12)所示，其中φ(E)＝∫ψ(E)dt为质子总辐射量，NIEL为非电离能量损失。NIEL实验数据通过原子量加权计算，不同E下的NIEL通过插值获得。Dd(E)＝φ(E)NIEL(E)(12)将辐射带运行过程中的位置参数离散为一系列节点{xk＝[Lk,lk]|x1,x2...xn}，并在节点处将质子能谱进行离散{E1,E2...Em}∈[2.8MeV,100MeV]。主要考虑能量位于2.8MeV～100MeV之间的质子对太阳翼的影响，节点处的位移损伤Dd(xk)为：太阳翼输出功率下降系数pr如式(14)所示，其中Dx和K的取值依材料而定。步骤F：建立以轨道转移总时间tf和太阳翼输出功率下降系数pr为目标的偏好函数并用遗传算法进行优化。设置轨道转移总时间以及太阳翼辐射输出功率下降系数的偏好与偏好类型，建立相应的偏好函数，根据流程利用遗传算法优化求解得到上述偏好的非劣解，从而得到全电推地球静止轨道航天器轨道转移的优化方案。有益效果考虑太阳翼辐射损伤的全电推两阶段地球静止轨道转移设计方法，针对全电推航天器轨道转移需要较长时间以及转移过程中太空辐射对太阳翼造成损伤的问题，提出了在减小太阳翼损伤情况下缩短轨道转移时间的策略，从而有效降低轨道转移过程中的太阳翼损伤，同时减少轨道转移时间，延长航天器工作寿命，为地球静止轨道航天器总体设计提供重要参考。本发明具有较强的工程实用性和较高的效率，适合应用到全电推地球静止轨道航天器的轨道转移设计中，有助于在降低太阳翼损伤的同时减小轨道转移时间，从而简化航天器控制系统设计，有效延长航天器寿命，为新一代全电推航天器的总体设计提供重要参考。附图说明图1为越小越好满意度区间图；图2为物理规划流程图；图3为轨道坐标系示意图；图4为一种考虑太阳翼辐射损伤的全电推地球静止轨道转移优化方法的流程图；图5为轨道转移第一阶段推力矢量方向角示意图；图6为轨道转移第二阶段推力矢量方向角示意图；图7为砷化镓材料NIEL拟合曲线；图8为轨道转移第一阶段仿真结果图；图9为轨道转移第二阶段仿真结果图；图10为太阳翼功率下降系数及轨道转移时间随推力矢量方位角变化图。具体实施方式下面结合附图与实施例，对本发明做进一步说明。为了更好地描述轨道转移涉及的模型，建立了如图3所示的坐标系。其中坐标系RTN原点位于航天器质心，R为轨道径向方向，N为轨道角动量方向，T与R、N垂直且指向运动方向；坐标系PQH原点位于地心，P指向近地点，H指向轨道角动量方向，Q与P、H成右手系；坐标系UVW为原点位于航天器质心，U沿航天器速度方向，V位于轨道面内垂直于速度且指向地心方向，W与U和V垂直且指向轨道面法向。一种考虑太阳翼辐射损伤的全电推航天器轨道转移优化方法，流程图如图4所示，具体实施方式如下：步骤A：给出轨道转移模型初始条件，包括推力器推力T、卫星初始发射质量m0、比冲为Tsp、推力器效率η，以及第一阶段轨道转移的初始轨道Kepler根数，包括轨道半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角ω和平近点角M。步骤B：建立轨道转移第一阶段模型。该阶段将轨道偏心率消除至0，同时降低轨道倾角。此阶段推力位于PQW系的QOW平面内，与-Q所成夹角为α，如图5所示。α的绝对值维持恒定，当轨道幅角u位于90°或270°时，改变α的正负。将电推力器产生的推力作为摄动力处理，建立轨道转移期间的Gauss型轨道摄动方程如式(15)所示。其中a、e、i、Ω、ω、M为轨道根数，f为真近点角，r为轨道半径，u＝ω+f为轨道幅角，p＝a(1-e2)为轨道通径，E为偏近点角,F＝[FR,FT,FN]为推力加速度在轨道坐标系RTN下的分量。由于推力加速度矢量定义在PQH坐标系中，因此需要通过坐标变换将加速度矢量[AR,AT,AN]T表示在RTN坐标系中，如式(16)所示。采用四五阶Runge-Kutta法对Gauss动力学方程进行求解，当偏心率小于0.01时，计算终止，当前时刻即为第一阶段轨道转移时间tf1。考虑地球辐射带对太阳翼的影响，需要输出航天器转移过程中位于辐射带时的位置参数以及运行时长，辐射带分布范围如表1所示。表1辐射带分布范围环境类别高度范围/km中心区域/km纬度范围/°内辐射带600～100003000～5000-40～40外辐射带10000～6000020000～25000-60～60为判断当前航天器运行位置是否位于辐射带内，需将Kepler根数转化为球坐标参数r、φ，转换方法如式(17)所示。第二阶段轨道转移模型轨道参数转换方法与此类似，不再详细描述。步骤C：建立第二阶段轨道转移模型。将第一阶段结束时的半长轴以及轨道倾角作为第二阶段的初始参数,并将第一阶段结束时航天器质量作为第二阶段轨道转移模型的初始质量。将推力加速度矢量固定在UVW坐标系中的UOW平面内，并与轨道平面保持方位角β，如图6所示。当u＝90°或270°时，β符号发生改变。采用庞特里亚金极小值原理对轨道最优控制问题进行求解，得到偏航角β的最优控制率如式(18)所示：其中v0为第二阶段轨道转移初始速度，A为推力加速度，初始偏航角β0计算方法如式(19)所示，其中i0为第二阶段初始轨道倾角。本阶段轨道转移所需的速度增量Δv计算公式如式(20)所示，其中vf＝3.075km/s为地球静止轨道速度，Δi为第二阶段轨道倾角变化量。得到的轨道转移时间tf2为：步骤D：输出轨道转移两阶段总时间。基于上述两阶段轨道转移模型，可以得到GTO-GEO转移总时间为：tf＝tf1+tf2(22)步骤E：建立太阳翼损伤模型。将卫星轨道转移阶段在辐射带中的位置参数及运行时长作为初始输入。全电推卫星在穿越VanAllen辐射带时会对太阳翼成损伤，该辐射带采用NASAAP8近似模型，VanAllen辐射带中质子全向辐射通量ψp为McIlwain坐标L和纬度l的函数，E为质子的能量，如式(23)所示：其中L＝r/(Rcos2l)，R＝6.378×106m为地球半径，r为辐射带位置坐标参数，a和b计算公式如式(24)所示，其中a0＝2.094×108cm-2s-1，a1＝-1.673MeV-2，a2＝-2.07，a3＝-2.825，b0＝-0.00971，b1＝0.0000982MeV-2，b2＝0.01484，b3＝0.0001561MeV-2，b4＝-0.004581，b5＝0.0004356。能量为E的质子产生的位移损伤Dd如式(25)所示，其中φ(E)＝∫ψ(E)dt为质子总辐射量，NIEL为非电离能量损失。砷化镓材料NIEL采用砷和镓的NIEL实验数据通过原子量加权计算，不同E下的NIEL通过插值获得，砷化镓材料NIEL拟合曲线如图7所示。Dd(E)＝φ(E)NIEL(E)(25)将辐射带运行过程中的位置参数离散为一系列节点{xk＝[Lk,lk]|x1,x2...xn}，并在节点处将质子能谱进行离散{E1,E2...Em}∈[2.8MeV,100MeV]。主要考虑能量位于2.8MeV～100MeV之间的质子对太阳翼的影响，节点处的位移损伤Dd(xk)为：太阳翼输出功率下降系数pr如式(14)所示，Dx＝3.52×109，K＝0.135。步骤F：建立以轨道转移总时间tf和太阳翼输出功率下降系数pr为目标的偏好函数并用遗传算法进行优化求解。设置轨道转移总时间tf的偏好以及太阳翼输出功率下降系数pr的偏好，设置两目标的偏好类型均为S型。根据图4所示的流程利用遗传算法求解得到上述偏好的非劣解。为了更加直观的说明本发明专利的有效性和工程实用性，下面以具体的全电推地球静止轨道卫星轨道转移优化问题为例，结合表格与附图作进一步说明。本案例中，卫星初始质量为2500kg，比冲为4000s，卫星有四个推力器，每个推力均为200mN。卫星初始GTO轨道的轨道根数中半长轴为24328km、偏心率为0.7296、轨道倾角为23.5°、升交点赤经为90°、近地点幅角为180°、平近点角为0°，推力矢量方位角的变化范围为0°到60°，初始方案的推力矢量方位角为30°。卫星轨道转移第一阶段轨道变化过程仿真结果如图8所示。以第一阶段终端时刻的轨道半长轴、轨道倾角和航天器质量作为第二阶段转移轨道模型的输入，轨道转移第二阶段轨道变化过程仿真结果如图9所示。在轨道转移结束后得到轨道转移第一阶段和第二阶段所需的轨道转移总时间tf。以上述轨道转移模型仿真结果为输入，由太阳翼损伤模型可得输出功率的下降系数pr。设置轨道转移总时间tf的偏好为[160173.75187.5201.252150000]，太阳翼输出功率pr下降系数的偏好为[0.2250.23750.250.26250.2750000]，两目标的偏好类型均为S型，建立以轨道转移时长和太阳电池功率下降系数为目标的偏好函数，采用遗传算法优化求解从而得到上述偏好对应非劣解。优化结束时轨道转移模型计算结果如表2所示，太阳翼功率下降系数以及轨道转移时间随推力矢量方位角变化情况如图10所示，只考虑轨道转移时间最短方案与本发明优化所得方案对比如表3所示。表2轨道转移模型计算结果相关参数/指标符号单位参数/指标值终端时刻半长轴akm42166.00终端时刻偏心率e-0.00终端时刻轨道倾角i°0.00表3初始方案与优化方案对比结果由表2可得，地球静止轨道卫星最终转移到了半长轴为42166km、偏心率为0、轨道倾角为0的地球静止轨道，与工程实际情况相符。由图10所示的结果可得，随着推力矢量方向角增大，太阳翼输出功率下降系数呈逐渐增大的趋势，在推力矢量方位角为10.2°时达到最小值22.37％；轨道转移时间先减少后增加，在推力矢量方位角为32.4°时达到最小值130.4天，因此太阳翼功率下降系数和轨道转移时间不能同时达到最小值，考虑地球输出功率的全电推地球静止轨道转移设计十分必要。由表3结果可得：轨道转移时间135.3天与太阳翼输出功率下降系数22.6％均在“期望”区域内，满足设计要求。相较于只考虑转移时间最短的方案，轨道转移时间增加4.9天，太阳翼输出功率下降系数降低1.83％，对于一个在轨寿命15年的卫星来说意味着工作时间增加4个月，说明本发明同时兼顾太阳翼损伤程度和轨道转移时间，从而有效延长航天器在轨寿命，能够为全电推航天器轨道转移设计提供有力支撑。此外，工程设计人员可以根据实际情况调整偏好，从而得到满足实际工程需求的轨道转移方案。以上所述的具体描述，对发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施例，用于解释本发明，并不用于限定本发明的保护范围，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3