FFT处理器及运算方法与流程

本发明涉及信号处理领域，特别涉及一种FFT处理器及运算方法。

背景技术：

傅里叶变换是一种将信号从时域变换到频域的变换形式，是信号处理的重要分析手段。离散傅里叶变换(Discrete Fourier Transform，简称“DFT”)是傅里叶变换在离散系统中的表示形式。但是DFT的计算量非常大。快速傅里叶变化(Fast Fourier Transformation，简称“FFT”)是一种DFT的高效算法，它根据DFT的奇、偶、虚、实等特性，对DFT算法进行改进而获得，从而大大减小了DFT算法的运算量。

FFT处理器是一种FFT算法的硬件结构，现有技术中，能够实现FFT处理器功能的方法有很多种，但大多存在一定的局限性。对于有些实现方法，只能支持单一点数的FFT运算，还有些方法则需要占用大量的资源，硬件电路面积较大。

技术实现要素：

本发明实施方式的目的在于提供一种FFT处理器及运算方法，使得多点FFT运算得以实现，增加FFT处理器的应用场景，同时占用较小电路面积，减低电路功耗，缩减电路成本。

为解决上述技术问题，本发明的实施方式提供了一种FFT处理器，包括：两个数据存储单元、旋转因子存储单元、多个蝶形运算单元、数据读写单元以及旋转因子读写单元；

数据读写单元连接于两个数据存储单元与各蝶形运算单元；两个数据存储单元分别用于均匀存放多个蝶形运算单元的N个输入数据与N个输出数据；其中，N＝2^k，k≥3且k为整数；

旋转因子读写单元连接于旋转因子存储单元与各蝶形运算单元；旋转因子存储单元用于存放N/2个旋转因子；

其中，数据读写单元用于逐个读取N个输入数据，并将逐个读取的N个输入数据依次输入多个蝶形运算单元；旋转因子读写单元用于逐个读取N/2个旋转因子，并将逐个读取的N/2个旋转因子依次输入多个蝶形运算单元；数据读写单元还用于逐个存储N个输出数据。

本发明的实施方式还提供了一种FFT运算方法，包括：

数据读写单元将从外部接收的N个输入数据均匀地存放在其中一个数据存储单元中；

旋转因子读写单元将从外部接收的N/2个旋转因子存放在旋转因子存储单元；

数据读写单元逐个读取N个输入数据，并将逐个读取的N个输入数据依次输入多个蝶形运算单元；

旋转因子读写单元逐个读取N/2个旋转因子，并将逐个读取的N/2个旋转因子依次输入多个蝶形运算单元；

各蝶形运算单元根据接收的各输入数据与各旋转因子运算得到各输出数据；

数据读写单元将各输出数据逐个存储至另一个数据存储单元；

其中，各输出数据作为下一级运算的各输入数据，且进行k级循环运算。

本发明实施方式相对于现有技术而言，数据均匀存放在两个数据存储单元中，对于不同点数的输入数据而言，可以采用同一读取规律进行读取，因此可以实现支持多点的运算。并且，数据读写单元逐个读取输入数据，并将逐个读取的输入数据依次输入多个蝶形运算单元，并将各蝶形运算单元的输出数据逐个存储，即同一时间内，有一个输入和一个输出数据，因此，只需要两个数据存储单元进行数据的存储，可以节省电路面积。

另外，蝶形运算单元的数目为4。通过4个蝶形运算单元循环工作的模式，最大程度的复用蝶形运算单元，可以尽可能的减小电路面积，并且4个蝶形运算单元从数据存储单元依次连续读取数据，可以避免运算单元的空闲，并且输出结果一直处于有效状态，从而有效地提高蝶形运算单元利用率。

另外，各蝶形运算单元包括1个乘法器和2个加法器；各蝶形运算单元用于实现基2蝶形运算。本实施方式中的各蝶形运算单元的结构较为简单，从而大大减小了电路面积。

另外，k的取值为k≤10。根据k配置的值不同，从而实现了支持不同点数的FFT处理器运算。

另外，各输入数据的存放地址依次递增；各数据存储单元包括1024个地址，当k＝10，N＝2¹⁰＝1024时，各输入数据依次存放；当k≤9时，各相邻输入数据的地址间隔相等。输入、输出数据均匀占据整个存储地址空间，方便计算，无需为不同点数的FFT处理器配置不同行计算方案。

另外，对于第i级运算，其中i＝0,1……，k，在数据读写单元逐个读取N个输入数据中，各输入数据的读取地址的产生方式包括：获取各输入数据对应的计数器二进制数列；将计数器二进制数列中的最后i+1位取倒数；将上述最后i+1位取倒数后的整个数据取倒数，以作为各输入数据的读取地址。对数据存储地址进行合理的分配，才能够完成正确的FFT运算。

附图说明

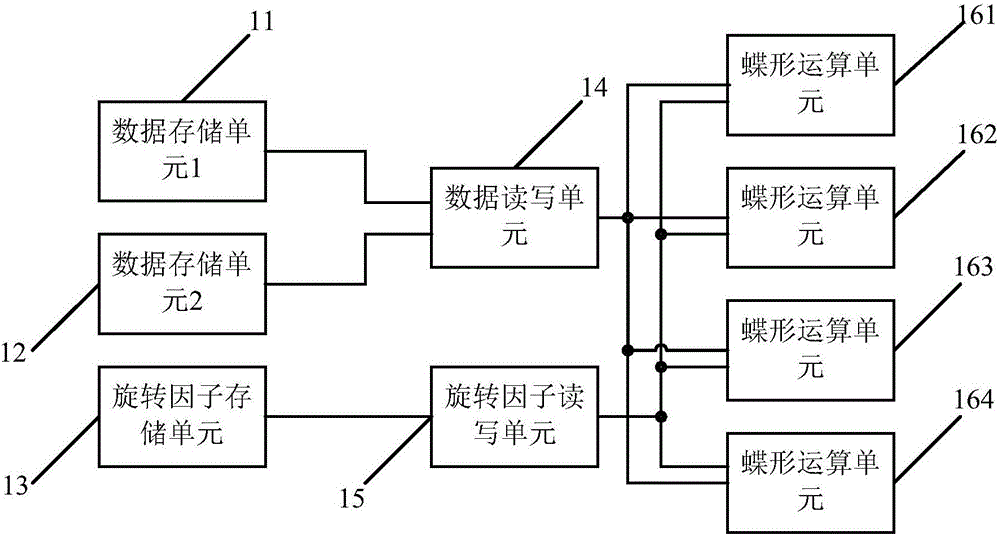
图1是根据本发明第一实施方式的FFT处理器的结构示意图；

图2是根据本发明第一实施方式的一种FFT处理器的蝶形运算单元内部运算过程的示意图；

图3是根据本发明第三实施方式的一种FFT运算方法的流程图；

图4是根据本发明第四实施方式的一种FFT运算方法中输入数据的读取地址产生方式的流程图；

图5是根据本发明第五实施方式的一种FFT运算方法中旋转因子的读取地址序列的产生方式的流程图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明的各实施方式进行详细的阐述。然而，本领域的普通技术人员可以理解，在本发明各实施方式中，为了使读者更好地理解本申请而提出了许多技术细节。但是，即使没有这些技术细节和基于以下各实施方式的种种变化和修改，也可以实现本申请所要求保护的技术方案。

本发明的第一实施方式涉及一种FFT处理器。具体结构示意图如图1所示，包括：两个数据存储单元11和12、旋转因子存储单元13、多个蝶形运算单元161至164、数据读写单元14以及旋转因子读写单元15；数据读写单元14连接于两个数据存储单元11和12与各蝶形运算单元161至164；旋转因子读写单元15连接于旋转因子存储单元13与各蝶形运算单元161至164。

其中，两个数据存储单元11和12，本实施方式中的两个数据存储单元可以为随机存取存储器(Random Access Memory，简称“RAM”)，两个RAM分别用于均匀存放多个蝶形运算单元161至164的N个输入数据与N个输出数据；其中，N＝2^k，k≥3且k为整数。数据读写单元14用于按照产生的地址序列逐个读取N个输入数据，并将按照产生的地址序列逐个读取的N个输入数据依次输入多个蝶形运算单元161至164。此外，数据读写单元14还用于逐个存储N个输出数据。

具体地说，在开始计算前，需要将蝶形运算单元161至164所需要用于计算的数据，导入到一个数据存储单元11中，例如导入数据存储单元11中，当FFT处理器的使能信号设置为高后，数据存储单元11根据所处的级数产生合适的地址序列，这个地址序列在数据存储单元11中对应的数据会作为输入数据，被数据读写单元14读取，并进行进一步的FFT运算，计算完毕后，数据读写单元14根据存储地址，将该输出数据存入数据存储单元12中，并且满足存储地址与在数据存储单元11中的读取地址一致，即参与计算的数据的读取地址与计算完毕数据的存储地址保持相同。

需要说明的是，数据读写单元14可以从数据存储单元11中读取输入的数据，也可以向数据存储单元11写入输出数据，同理对于数据存储单元12也可以做如此操作，数据存储单元采用乒乓RAM的形式来缩小所消耗的资源，即数据存储单元11或12，既可以作为输入数据的存储单元，也可以作为输出数据的存储单元，并且数据是均匀存储在数据存储单元11、12中的，可以理解为，输入或输出数据在数据存储单元11或12中存放的地址对应相等。

本实施方式中的FFT处理器采用基2的算法，N为FFT处理器支持的运算点数，其中，N＝2^k，k≥3且k为整数；则N的最小值为8，说明最小支持8点的FFT运算，并且基2算法总共有k级运算。k设置的值不同，即FFT运算点数N不同，即运算级数也不同。其中，对于每一级运算，都需要数据读写单元14从其中一个数据存储单元中读取数据，并将计算后蝶形单元的输出数据存储到另一个数据存储单元中，而进行下一级运算时，数据读写单元14从上一级存入数据的数据存储单元中读取数据，将计算后蝶形单元的输出数据存储到上一级读取数据的数据存储单元中。例如，数据读写单元14从数据存储单元11中读取数据，并将计算后蝶形单元的输出数据存储到数据存储单元12中，而进行下一级运算时，数据读写单元14从数据存储单元12中读取数据，将计算后蝶形单元的输出数据存储到数据存储单元11中。

此外，FFT处理器运算过程中的参数，可以由用户进行配置。

本实施方式中，旋转因子存储单元13用于存放N/2个旋转因子。

在开始计算前，需要将蝶形运算单元161至164所需要用于计算的旋转因子表导入到对应的旋转因子存储单元13中，更加具体地说，根据可以知道对于最多支持1024点FFT处理器而言，其所需要用的旋转因子均可转化为其中N的取值范围为0-511，将实部与虚部做有符号数的16位宽(bit)量化，将量化的结果分别存储在旋转因子存储单元13中。对于每两个输入信号而言，仅需要一个旋转因子运算得出输出数据，因此，对于支持N点的FFT处理器，需要N/2个旋转因子。

一般而言，旋转因子存储单元13可以分成两块，用其中一块存储单元存储旋转因子的实部，用另一块存储单元来存储旋转因子的虚部，每个相同地址的数据一一对应。然不限于此，在实际应用中，也可以使用该旋转因子存储单元13的高低位分别存储旋转因子的实部和虚部。此外，旋转因子可以以表格的形式，事先存入旋转因子存储单元13中，在运算过程中需要用到旋转因子时，从预先导入旋转因子存储单元13中的旋转因子表格中读取对应的旋转因子，进行进一步的计算。

进一步的，旋转因子读写单元15用于按照产生的地址序列逐个读取N/2个旋转因子，并将按照产生的地址序列逐个读取的N/2个旋转因子依次输入多个蝶形运算单元161至164。

具体地说，在运算过程中需要用到旋转因子时，通过给出的旋转因子地址信号和读使能，旋转因子读写单元15来读取旋转因子的值，旋转因子地址每两个周期变化一次，通过控制逻辑来实现。旋转因子读写单元15将按照产生的旋转因子的地址序列逐个读取的N/2个旋转因子，并依次输入多个蝶形运算单元161至164，进行进一步的计算。

此外，蝶形运算单元161至164的N个输入数据由数据读写单元14从数据存储单元11或12中读取得来，每一个蝶形运算单元，如蝶形运算单元161需要2个周期获取输入数据，且N/2个旋转因子由旋转因子读写单元15读取并写入蝶形运算单元161，而N/2个旋转因子的实部和虚部分别按高低位存储在旋转因子存储单元13中，可与N个输入数据同时获得。其中，本实施方式中所需的周期具体指代时间周期。

对于一个蝶形运算单元161，在其内部需要做相应运算，并得到输出数据，如公式(1)和(2)：

其中，x1(k)和x2(k)分别为输入数据，为旋转因子，x(k)和x(k+N/2)为经过蝶形运算单元161的输出数据。

则整个蝶形运算单元的计算过程如图2所示，其输出数据分别为：x(k)和x(k+N/2)。将每个输出数据写作实部和虚部的形式，如公式(3)和(4)：

out1＝(x_a+x_bx_c-y_by_c)+(y_a+x_by_c+x_cy_b)j (3)

out2＝(x_a-x_bx_c+y_by_c)+(y_a-x_by_c-x_cy_b)j (4)

其中xa,xb,xc分别为x1(k),x 2(k),的实部，ya,yb,yc为x1(k),x2(k),的虚部。

值得一提的是，对于每个蝶形运算单元，如蝶形运算单元161，包括1个乘法器和2个加法器，2个输出out1和out2的实部和虚部全部计算完毕需要7个周期。计算过程为：

第一个周期，乘法器计算xb*xc，结果记为mul_out；

第二个周期，1号加法器计算xa+xb*xc，2号加法器计算xa-xb*xc，而乘法器计算yb*yc，结果同样存入mul_out；

第三个周期，1号加法器计算xa+xb*xc-yb*yc，这就是第一个输出out1的实部。同时，2号加法器计算xa-xb*xc+yb*yc，这就是第二个输出out2的实部，乘法器计算xb*yc；

第四个周期，1号加法器计算ya+xb*yc，2号加法器计算ya-xb*yc，乘法器计算xc*yb；

第五个周期，1号加法器计算ya+xb*yc+xc*yb，此时out1输出的虚部计算完成，2号加法器计算ya-xb*yc-xc*yb，此时out2输出的虚部计算完成。

从上述分析我们可以看出2个输出out1和out2的实部是同时计算完成的，在计算完成后，需要把蝶形运算单元的输出数据通过数据读写单元14存储在数据存储单元11或12中，而数据存储单元11或12的一个周期仅能写入一个数据，因此可以将第三个周期和第五个周期中2号加法器的输出作一拍延迟，这样可以在第3个周期的时候，得到输出out1的实部，第4个周期的时候得到输出out2的实部，第5个周期的时候得到输出out1的虚部，第6个周期的时候，得到输出out2的虚部，从而满足数据存储单元11或12的存储要求。

由于计算结果为17位数据，而数据存储单元11或12仅能存储16位，因此需要对计算结果作截位处理，舍去最低的1位，即相当于将输出结果除以2，对于每一级结果均进行如此操作，总共k级，因此最终的结果被缩小了N倍，但是由于它们之间相对大小不受影响，因此依然可以通过最后的频谱分布来确定频率。

此外，由于输出数据的写地址与输入数据的读地址需要保持一致，所以对于每个蝶形运算单元161，我们都要缓存2个输入数据的地址直至计算完毕，唯一例外的地方在于最后一级，最后一级需要把输出数据序列再进行一次排列来获得正确的存储顺序，例如对于1024点的FFT处理器而言，最后1级第一个蝶形运算单元的输入地址为0、1，而输出地址应该为0、512(k和k+N/2总是成对出现)，因此需要加入一级额外的判断来达到输出序列正确顺序的目的。

值得一提的是，蝶形运算单元的数目为4。

具体地说，本实施方式中FFT处理器的整个蝶形运算部分为4个蝶形运算单元的叠加，每个蝶形运算单元从数据存储单元11或12中取出两个数进行计算，如果将蝶形运算单元161至164阵列参与运算，则会发现当第4个蝶形运算单元开始工作时，第一个蝶形运算单元工作完毕，可以开始准备下一次取数，4个蝶形运算单元即可满足从数据存储单元11或12中依次连续取数的要求，所以可以通过用4个蝶形运算单元循环工作的模式，来完成每一级所需要的蝶形运算。此种方式的电路面积最小。其中，每一级的运算都由N/2个蝶形运算单元组成。

此外，本实施方式中FFT处理器的整个蝶形运算部分为4个蝶形运算单元的叠加，则每8个周期为一次循环(每个蝶形运算单元需要2个周期完成输入数据的读取，则4个依次工作的蝶形运算单元需要8个周期)，进行N/8次循环后，一级中的N/2个蝶形运算计算完毕，由于在最后一个运算单元读取数据后还需要7个周期进行运算来得到最后的输出数据，因此每一级的时间可以设置为N(读取数据的时间)+7(最后读取完毕需运算的时间)+1(读地址与读数据之间延迟的一拍)＝N+8个周期。

根据前面分析，对于支持1024点的FFT处理器而言，一级运算需要1032个周期，计数器从0-1031来表示这1032个周期，其中0-1023周期在从数据存储单元11或12中读取信号，此时读使能为高，而对于4个蝶形运算单元循环计算模式，每8个周期为一个循环，因此这样每8个周期便可出现一次，而其他的输入使能均依次延迟一个周期，这样便依次得到了4个蝶形运算单元全部的8个输入使能。

而对于输出数据而言，根据前面的分析，一个蝶形运算单元输出分为实部和虚部，实部输出使能和虚部输出使能均持续2个周期，而蝶形运算单元输入恰恰需要2个周期来读取数据，因此下一个蝶形运算的结果正好比上一个蝶形运算单元的结果晚出来2个周期，因此对于整体而言，输出结果一直处于有效状态，对于实部输出和虚部而言，每8个周期为一个循环，依次输入第一个，第二个，第三个，第四个蝶形运算单元的运算结构，直至此轮计算完毕。

需要说明的是，本实施方式中，采用4个蝶形运算单元循环工作的模式，则4个蝶形运算单元可以做为最小的基本运算单元，又由于每两点的输入数据，需要一个蝶形运算单元，因此，最小可以支持N为8点的FFT处理器运算，结合N＝2^k，可以理解，k为≥3的整数。

本实施方式相对与现有技术而言，其主要的区别和效果在于：数据均匀存放在两个数据存储单元中，对于不同点数的输入数据而言，可以被以同一规律进行读取，因此可以实现支持多点的运算。数据读写单元按照产生的地址序列逐个读取输入数据，并将按照产生的地址序列逐个读取的输入数据依次输入多个蝶形运算单元，并且数据读写单元会逐个存储输入、输出的数据，同一时间内，有一个输入和一个输出数据，因此，只需要两个数据存储单元进行数据的存储，可以节省电路面积。

值得一提的是，本实施方式中所涉及到的各模块均为逻辑模块，在实际应用中，一个逻辑单元可以是一个物理单元，也可以是一个物理单元的一部分，还可以以多个物理单元的组合实现。此外，为了突出本发明的创新部分，本实施方式中并没有将与解决本发明所提出的技术问题关系不太密切的单元引入，但这并不表明本实施方式中不存在其它的单元。

本发明的第二实施方式涉及一种FFT处理器。第二实施方式是第一实施方式的进一步优化，主要优化之处在于：在本发明第二实施方式中，k的取值为k≤10，且各输入数据的存放地址依次递增。各数据存储单元包括1024个地址，当k＝10，N＝2¹⁰＝1024时，各输入数据依次存放；当k≤9时，各相邻输入数据的地址间隔相等。可以得知，此外，根据k的取值不同，可以实现支持8-1024点的FFT处理器，即在不改变现有设备硬件环境下，例如，不改变数据存储器的空间容量或地址信号位宽的情况下，可以实现支持最大点数范围的FFT运算。

具体地说，在计算低点数的FFT过程中，将需要计算的数据写入数据存储单元中的地址并不是连续的，例如，对于512点FFT处理器，数据写入数据存储单元中地址是0、2、4、6…1022这样跳变，而对于256点FFT，数据写入数据存储单元中的地址则是0、4、8、16...1020这样变化，它们满足的核心思想便是需要将数据均匀的占据整个地址空间，而不是连续的写在地址空间中的某一块中，对于均匀存放数据方式的具体限定，使得数据以同一规律被读取，从而实现支持多点FFT运算。

需要说明的是，本实施方式不仅仅支持最大1024点的FFT处理器计算，还可以支持超过1024点的FFT处理器的运算。如果需要支持更高点数的FFT处理器运算，需要改动的仅仅是定义更高k级数，以及更大的数据存储单元和更大bit的地址信号而已。

本实施方式相对与现有技术而言，其主要的区别和效果在于：在不改变现有设备硬件环境下，例如，不改变数据存储器的空间容量或地址信号位宽的情况下，可以实现支持最大点数范围的FFT运算。

本发明第三实施方式涉及一种FFT运算方法，如图3所示，包括：

步骤301：数据读写单元将从外部接收的输入数据均匀存放在数据存储单元。

具体地说，数据读写单元将从外部接收的N个输入数据均匀地存放在其中一个数据存储单元中。N的数值为本实施方式中FFT处理器可以支持的点数，N可以在不改变现有设备情况下，在允许点数的最大范围内进行取值。并且，数据存储单元中，预先导入要进行FFT运算的N个输入数据，N个输入数据均匀存放在一个数据存储单元中，其中，均匀分布可以理解为，需存储数据在数据存储单元中的地址间隔是一样的，从而保证数据以相同规律被读取，实现支持多点的运算。

步骤302：旋转因子读写单元将从外部接收的旋转因子存放在旋转因子存储单元。

具体的说，旋转因子读写单元将从外部接收的N/2个旋转因子存放在所述旋转因子存储单元。由于在FFT运算过程中，每两个输入数据共同使用一个旋转因子，如果输入数据为N个，则需要N/2个旋转因子，才可以进行FFT运算。并且，N/2个旋转因子是以旋转因子表的形式通过旋转因子读写单元预先存入旋转因子存储单元中。

需要说明的是，步骤301和步骤302之间并没有严格的逻辑顺序，可以进行顺序的互换，数据读写单元将输入数据存放在数据存储单元与旋转因子读写单元将数据存放在旋转因子存储单元的执行顺序前后，并不会对FFT运算的结果造成任何的影响。

步骤303：数据读写单元逐个读取输入数据，并将其依次输入蝶形运算单元。

具体地说，数据读写单元按照产生的地址序列逐个读取N个输入数据，并将按照产生的地址序列逐个读取的N个输入数据依次输入多个蝶形运算单元。数据读写单元从其中一个数据存储单元中获取N个输入数据，并将获取的N个输入数据存入多个蝶形运算单元。其中，基本的蝶形运算单元为4个蝶形运算单元。由于数据读写单元逐个读写数据，因此，同一时间，只有一个输入和一个输出数据，则只需要两个数据存储单元进行数据存储，节省电路占用面积。

步骤304：旋转因子读写单元逐个读取旋转因子，并将其依次输入蝶形运算单元。

具体地说，旋转因子读写单元按照产生的地址序列逐个读取N/2个旋转因子，并将按照产生的地址序列逐个读取的N/2个旋转因子依次输入多个蝶形运算单元。通过旋转因子读写单元，在旋转因子存储单元中，读取出N/2个旋转因子，并将读取出的N/2个旋转因子输入多个蝶形运算单元。

需要说明的是，步骤303和步骤304之间并没有严格的逻辑顺序，可以进行顺序的互换，数据读写单元读取输入数据并存入蝶形运算单元与旋转因子读写单元读取旋转因子并存入蝶形运算单元的执行顺序先后，并不会对FFT运算的结果造成任何的影响。

步骤305：蝶形运算单元运算得到输出数据。

具体地说，各蝶形运算单元根据接收的各输入数据与各旋转因子运算得到各输出数据。利用4个蝶形运算单元作为一个基本的单元循环，通过数据读写单元和旋转因子读写单元不停从数据存储单元与旋转因子存储单元中读取和写入数据的基本结构，输入数据与旋转因子不断的被选取，随后被计算，随后输出数据，仅仅只需要对每一级读取的写入的地址进行相应的转换，便可以通过不停复用基本运算单元来完成整个FFT运算操作，并且减少空闲的等待时间。

步骤306：数据读写单元将输出数据存储至数据存储单元。

具体的说，数据读写单元将各输出数据逐个存储至另一个数据存储单元。其中，步骤301中在数据存储单元中读取的数据地址与本步骤中存入另一个数据存储单元的数据地址，需要保持一致，才能方便对读写数据进行操作。

步骤307：计数器记录当前循环级数。

具体地说，数据读写单元在每完成一次输出数据存储时，计数器自动记录当前循环级数。其中，计数器的初始值为0，则代表初始运算时循环级数为0，在每完成一次输出数据存储时，计数器自动加一，并将加一后的结果重新保存在计数器中。

步骤308：判断当前循环级数与k值是否相等。

具体地说，判断计数器中保存的当前值是否等于k值，如果等于，则进入步骤309中，如果不等，则进入步骤303。如果计数器中的值与k值相同，则说明已经完成全部的FFT运算，并进入步骤309中。否则，说明当前循环级数小于k值，即还未完成k级循环运算，则进入步骤303中，重新获取下一级的输入数据和旋转因子，并将它们输入蝶形运算单元，直至完成所有k级的运算为止。

其中，各输出数据作为下一级运算的各输入数据，并且在步骤301和步骤302中，由于从外部接收的输入数据和旋转因子分别预先存入数据存储单元和旋转因子存储单元，因此，并不进入k级循环计算中。

步骤309：清空计数器。

具体的说，当循环级数等于k值时，即已经完成了k级运算，则清空计数器的值，在下次FFT运算中，重新计数，即重新计算运算级数。

本实施方式中含有2个相同的数据存储单元，两个数据存储单元既可存储输入数据，也可以存储输出数据，2个数据存储单元以乒乓RAM的形式进行数据的存储。可以理解为，对于每一级的FFT运算，需要从第一个数据存储单元中获取输入数据，并将计算后的结果输出到第二个数据存储单元，下一级的FFT运算就将从第二个数据存储单元中获取输入数据，并将计算后的输出数据第一个存入数据存储单元中。

其中，k的值的选取可以确定FFT运算可以支持的点数，并且FFT运算共运行k级循环。

本实施方式相对与现有技术而言，其主要的区别和效果在于：数据均匀存放在两个数据存储单元中，对于不同点数的输入数据而言，可以采用同一读取规律进行读取，因此可以实现支持多点的运算。数据读写单元按照产生的地址序列逐个读取输入数据，并将按照产生的地址序列逐个读取的输入数据依次输入多个蝶形运算单元，并将各蝶形运算单元的输出数据逐个存储，即同一时间内，有一个输入和一个输出数据，因此，只需要两个数据存储单元进行数据的存储，可以节省电路面积。

不难发现，本实施方式为与第一实施方式相对应的方法实施例，本实施方式可与第一实施方式互相配合实施。第一实施方式中提到的相关技术细节在本实施方式中依然有效，为了减少重复，这里不再赘述。相应地，本实施方式中提到的相关技术细节也可应用在第一实施方式中。

本发明第四实施方式涉及一种FFT运算方法。第四实施方式是第三实施方式进一步优化，主要优化之处在于：在本发明第四实施方式中，提供了一种输入数据的读取地址的产生方式；即，对于第i级运算，其中i＝0,1……，k，在数据读写单元按照产生的地址序列逐个读取N个输入数据中，本实施方式提供的各输入数据的读取地址的产生方式可以保证读取数据的正确性。其中，对第三实施方式中步骤303数据读写单元逐个读取N个输入数据中，各输入数据地址产生方式的流程图，如图4所示，包括：

步骤401：获取个输入数据对应的计数器二进制数列。

具体地说，获取各输入数据对应的计数器二进制数列。通过数据读写单元获取的输入数据为十进制的数据，在获取到十进制的输入数据后，将十进制的输入数据转化为二进制的输入数据。例如，获取的十进制的输入数据地址为“1”。由于在本实施方式中，k的取值为小于等于10，如果k的取值为10，即N＝1024。获取的十进制数据地址为“1”对应转换后的二进制输入数据地址为“0000000001”。

步骤402：将计数器二进制数列中的最后i+1位取倒数。

具体地说，对于i为第0级，则步骤401中获取的二进制输入数据地址通过本步骤后，输出为“0000000001”；

对于i为第1级，则步骤401中获取的二进制输入数据地址通过本步骤后，输出为“0000000010”

步骤403：将最后i+1位取倒数后的整个数据取倒数，以作为各输入数据的读取地址。

具体地说，对于i为第0级，则步骤402中获取的二进制输入数据地址通过本步骤后，输出的二进制数据地址为“1000000000”，对应的十进制的数据地址为“512”；

对于i为第1级，则步骤402中获取的二进制输入数据地址通过本步骤后，输出的二进制数据地址为“0100000000”，对应的十进制的数据地址为“256”。

可以看出，读地址的选取规律：对于第k级，输入数据地址序列为计数器二进制数列取最后k+1位的倒数后再将整个数据变为倒数。

以1024点FFT运算为例，我们首先通过做一个计数器从0计数到1023，对这个序列进行对应的读地址转换，转换出来的序列为0、512、256、768…则意味着送入第一个蝶形运算单元中的数据为地址0和地址512中的数据，送入第二个蝶形运算单元中的数据为地址256和地址768中的数据，依次类推，数据按照此规律依次送入蝶形运算单元中，并在计算完毕后依次被取出。

本实施方式相对与现有技术而言，其主要的区别和效果在于：对数据存储地址进行合理的分配，保证完成正确的FFT运算。

本发明第五实施方式涉及一种FFT运算方法。第五实施方式是第三实施方式进一步优化，主要优化之处在于：在本发明第五实施方式中，对于第i级运算，在旋转因子读写单元按照产生的地址序列逐个读取N/2个旋转因子中，N/2个旋转因子的读取地址序列的产生方式。其中，对第三实施方式中步骤304旋转因子读写单元按照产生的地址序列逐个读取N/2个旋转因子中，各旋转因子地址产生方式的流程图，如图5所示，包括：

步骤501：生成计数序列。

具体地说，生成一个计数序列，计数序列表示为：0、1、2、3、……、2ⁱ-1。可以理解，对于第0级，即i＝0时，计数序列为0、0、0…

对于第1级，计数序列为0、1、0、1…；

对于第2级，计数序列为0、1、2、3、0、1、2、3…；

对于第i级，计数序列为0、1、2、3、…2ⁱ-1、0、1、2、3…

步骤502：将计数序列取倒数作为旋转因子读取地址序列。

具体地说，将计数序列0、1、2、3、……、2ⁱ-1取倒数后表示为：0、512、256、768……，以作为N/2个旋转因子的读取地址序列。例如，对于第2级，计数序列为0、1、2、3、0、1、2、3…，取倒数后表示为：0、512、256、768、0、512、256、768…

旋转因子的地址选取方式的原理在于因此对于每一级所需要的选取的旋转因子值，均能转化为其中k的取值范围为0-511，这样只需要有一块1KB的存储单元,则可存入所有的旋转因子，同时根据地址的变化，读出合适的旋转因子送入蝶形运算单元进行运算。通过分析FFT算法中旋转因子在每一级的取值，并将它们转化成同时将k作为从存储单元中读取选旋转因子所使用的地址，地址序列满足一定的规律，对规律进行总结可以得到如本实施方式介绍的地址产生方式。

上面各种方法的步骤划分，只是为了描述清楚，实现时可以合并为一个步骤或者对某些步骤进行拆分，分解为多个步骤，只要包括相同的逻辑关系，都在本专利的保护范围内；对算法中或者流程中添加无关紧要的修改或者引入无关紧要的设计，但不改变其算法和流程的核心设计都在该专利的保护范围内。

本领域技术人员可以理解实现上述实施例方法中的全部或部分步骤是可以通过程序来指令相关的硬件来完成，该程序存储在一个存储介质中，包括若干指令用以使得一个设备(可以是单片机，芯片等)或处理器(processor)执行本申请各个实施例所述方法的全部或部分步骤。而前述的存储介质包括：U盘、移动硬盘、只读存储器(ROM，Read-Only Memory)、随机存取存储器(RAM，Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。

本领域的普通技术人员可以理解，上述各实施方式是实现本发明的具体实施例，而在实际应用中，可以在形式上和细节上对其作各种改变，而不偏离本发明的精神和范围。