一种基于元胞自动机模型的沥青混合料破坏演化仿真方法与流程

本发明属于道路材料技术领域，具体涉及一种基于元胞自动机模型的沥青混合料破坏演化仿真方法。

背景技术：

由于沥青混合料内部存在大量强度不同的微观缺陷、微裂隙等软弱区，造成沥青混合料微观结构上的非均质性和各向异性。沥青混合料的均匀性对路面的使用寿命和路用性能有很大影响，沥青混合料破坏是一个复杂的过程，须从微观的角度出发研究其破坏过程。在破坏过程中应力与应变呈非线性变化，由于材料细观结构的非均质性，破坏过程主要包括微裂纹的张开、扩展直至破坏，也表现出很强的非线性特性。因此，很难通过传统的宏观模型对其进行有效的实时动态模拟。

技术实现要素：

针对现有技术存在的问题，本发明提供一种基于元胞自动机模型的沥青混合料破坏演化仿真方法。本发明的技术方案为：

一种基于元胞自动机模型的沥青混合料破坏演化仿真方法，包括以下步骤：

获取沥青混合料各个点的屈服强度；

采用weibull分布法对沥青混合料各个点的屈服强度进行数据拟合，得到沥青混合料屈服强度的概率分布参数；

对沥青混合料各个点的屈服强度进行统计，以构建元胞自动机模型运行的元胞空间，并确定所述元胞空间中每个元胞的邻居结构；

初始化每个元胞的状态，其中元胞的初始状态为完整状态，用1表示；最终状态为破坏状态，用0表示；

定义每个元胞的初始能量和每个时步的加载能量，并根据概率分布参数给每个元胞赋予破裂阈值，开始对元胞进行能量输入；

判断各元胞的状态为1还是0，如果为1则继续加载能量，如果为0则将能量分配给邻居元胞并判断邻居元胞的状态为1还是0，继续处理，直到所有元胞状态达到0为止。

上述方法中，所述概率分布参数为沥青混合料屈服强度的总体平均值和沥青混合料的均质程度，分别用λ和k表示，并且λ和k满足以下关系式：其中为不同元胞屈服强度的分布密度；x为沥青混合料的屈服强度。

上述方法中，所述元胞空间为由n×n个四边形单元组成的二维矩阵，每个四边形单元为一个元胞；其中，n为整数，表示一维上的四边形个数。

上述方法中，所述每个元胞的邻居结构为8邻居结构。

上述方法中，所述每个时步的加载能量优选为0.01的单位应力。

上述方法中，所述判断各元胞的状态为1还是0，方法为：t时步内每个元胞的总加载能量小于每个元胞的破裂阈值，则为1；否则为0。

本发明的有益效果在于：本发明利用计算机仿真技术可模拟沥青混合料的破坏过程，为研究沥青混合料破坏提供了一种新方法，工艺简单，运行费用较低，对促进行业技术进步有着显著的意义。

附图说明

图1为本发明实施例的工艺流程图。

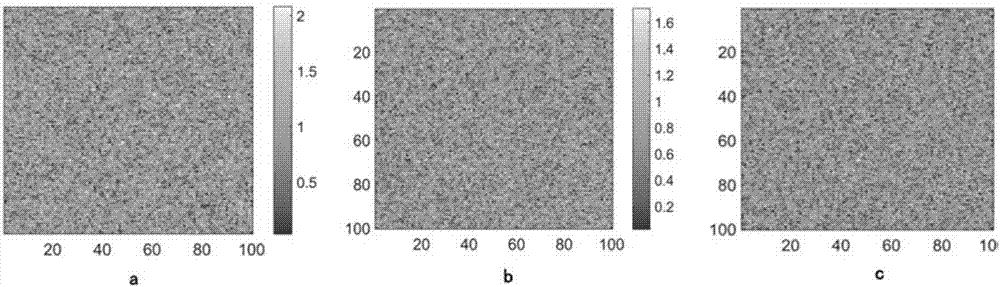
图2为本发明实施例的元胞不均匀性仿真效果图，其中a为λ＝3，k＝1.0时元胞不均匀性仿真效果图；b为λ＝3，k＝2.0时元胞不均匀性仿真效果图；c为λ＝3，k＝3.0时元胞不均匀性仿真效果图。

图3为本发明实施例的元胞单元强度的个数统计图，其中a为λ＝3，k＝1.0时元胞单元强度的个数统计图；b为λ＝3，k＝2.0时元胞单元强度的个数统计图；c为λ＝3，k＝3.0时元胞单元强度的个数统计图。

图4为本发明实施例的沥青混合料破坏演化图，其中a为λ＝3，k＝1.0时沥青混合料的破坏演化图；b为λ＝3，k＝2.0时沥青混合料的坏演化图；c为λ＝3，k＝3.0时沥青混合料的坏演化图。

具体实施方式

下面结合附图和具体的实施例对本发明做进一步详细说明，所述是对本发明的解释而不是限定。

本发明提供一种基于元胞自动机模型的沥青混合料破坏演化仿真方法，其工艺流程图如图1所示，包括以下步骤：

获取沥青混合料各个点的屈服强度；

采用weibull分布法对沥青混合料各个点的屈服强度进行数据拟合，得到沥青混合料屈服强度的概率分布参数：沥青混合料屈服强度的总体平均值和沥青混合料的均质程度，分别用λ和k表示，并且λ和k满足以下关系式：其中为不同元胞屈服强度的分布密度；x为沥青混合料的屈服强度；

对沥青混合料各个点的屈服强度进行统计，以构建元胞自动机模型运行的元胞空间，并确定所述元胞空间中每个元胞的邻居结构为8邻居结构；所述元胞空间为由n×n个四边形单元组成的二维矩阵，每个四边形单元为一个元胞；其中，n为整数，表示一维上的四边形个数；

初始化每个元胞的状态，其中元胞的初始状态为完整状态，用1表示；最终状态为破坏状态，用0表示；

定义每个元胞的初始能量和每个时步的加载能量，并根据概率分布参数给每个元胞赋予破裂阈值，破裂阈值即为沥青混合料的屈服强度，开始对元胞进行能量输入；所述每个时步的加载能量优选为0.01的单位应力；

判断各元胞的状态为1还是0，如果为1则继续加载能量，如果为0则将能量分配给邻居元胞并判断邻居元胞的状态为1还是0，继续处理，直到所有元胞状态达到0为止。其中判断各元胞的状态为1还是0的方法为：t时步内每个元胞的总加载能量小于每个元胞的破裂阈值，则为1；否则为0。

实施例1

获取沥青混合料各个点的屈服强度；

采用weibull分布法对沥青混合料各个点的屈服强度进行数据拟合，得到沥青混合料屈服强度的概率分布参数：沥青混合料屈服强度的总体平均值和沥青混合料的均质程度，分别用λ和k表示，并且λ和k满足以下关系式：其中为不同元胞屈服强度的分布密度；x为沥青混合料的屈服强度；当λ＝3，k＝1.0、2.0、3.0时，元胞的不均匀性仿真效果图如图2所示，元胞单元强度的个数统计图如图3所示；

对沥青混合料各个点的屈服强度进行统计，利用matlab将沥青混合料二维界面离散成50×50个等同四方形单元的元胞空间，每个单元为一个元胞，用(xi，yj)(i，j＝1，…，n)表示，n为整数，表示一维上的四边形单元个数；并确定所述元胞空间中每个元胞的邻居结构为8邻居结构；每个元胞分为完整和破坏两个状态；

初始化每个元胞的状态，其中元胞的初始状态为完整状态，用1表示；最终状态为破坏状态，用0表示；

以e(xi，yj，t)表示t时步元胞(xi，yj)所具有的广义能量，等效于该元胞所具有的弹性应变能；以e(xi，yj，0)表示元胞的初始能量，等效于元胞的初始应力。根据概率分布参数给元胞赋予破裂阈值emax(xi，yj，t)，等效于元胞发生破坏的极限强度。以n(t)表示第t时步整个系统元胞破裂的总个数。在每个时步t内给元胞输入能量，等同于应力增大，每个时步的加载能量优选为0.01的单位应力；

判断各元胞的状态为1还是0，如果为1则继续加载能量，如果为0则将能量分配给邻居元胞并判断邻居元胞的状态为1还是0，继续处理，直到所有元胞状态达到0为止。其中判断各元胞的状态为1还是0的方法为：t时步内每个元胞的总加载能量小于每个元胞的破裂阈值，则为1；否则为0，即e(xi，yj，t)≥emax(xi，yj，t)。

元胞发生破裂，将其能量释放到周围元胞，能量进行重新分配，计算邻居元胞能量。判断是否有邻居元胞能量达到破裂阈值，直至所有元胞发生破裂。

本发明的仿真过程，假定能量的输入是绝热的，在输入能量后，元胞接受能量被激活，达到极限强度，则进行能量传递，直至没有元胞再被激活，系统再从外界获取能量。能量的扩散传递是并行进行的，即当系统同时有多个元胞破裂时，能量的扩散将同时进行。系统在演化过程中满足能量守恒定律，如果系统边界元胞的邻居个数少于8个或者元胞的邻居元胞中有破裂的，则元胞在传递能量时，根据缺少的邻居元胞个数将一定的能量作为系统所耗散的能量处理。图4a为λ＝3，k＝1.0时材料的破坏演化图，4b为λ＝3，k＝2.0时材料的破坏演化图，图4c为λ＝3，k＝3.0时材料的破坏演化图。

应当理解的是，对本领域普通技术人员而言，可以根据上述说明加以改进或变换，而所有这些改进和变换都应落入本发明要求的保护范围内。