一种结合公共空间模式算法和EMD的脑电信号特征提取方法与流程

本发明属于智能信息处理领域，具体涉及一种结合公共空间模式算法和EMD(经验模式分解)的脑电信号特征提取方法。

背景技术：

脑机接口是一种基于脑电信号实现人脑与计算机或其他设备之间通信和控制的接口，通过大脑活动产生的脑电信号(Electroencephalogram,EEG)为人类和环境之间提供了新的通信和控制渠道，拓宽了人类的控制能力，具有广泛的应用前景。该领域的发展不仅帮助瘫痪病人使用计算机、神经假体、机器臂等电子设备，也实现了包括：运动恢复、通信、环境控制甚至娱乐等其他功能。

目前，基于EEG的脑机接口主要包含五个主要步骤：获取信号、预处理、特征提取、特征分类和接口设备控制。在以上步骤中：因为有效地在降维特征空间展现了输入信号特征并适用于进一步标识不同想象运动脑电信号的判别信息，特征提取在BCI 研究界受到广泛的关注。

作为基于运动想象的脑机接口(Motor Imagery-Brain Computer Interface,MI-BCI)系统的信号源，包括脑电图(EEG)和脑皮层电图(Electrocorticography,ECoG)，EEG信号是一种弱的、非线性、非平稳并且随时间变化的信号。所以提出一种有效的特征提取方法是改善识别精度的关键。目前，时间-频率分析作为处理智能信号一种潜在的强大方法并且被广泛地应用于脑信号的研究。传统的时间-频率方法包括：短时傅里叶变换 (Short-time Fourier Transform,STFT)，小波变换(Wavelet Transform,WT)，Winger-Ville 分布，但是这些方法的本质都是基于傅里叶变换，根据海森堡不确定性原理，该方法不可能同时得到时间-频率的良好分辨率。近年，希尔伯特黄变换 (Hilbert-Huang Transform,HHT)作为另一种时间-频率分析法已经变得越来越流行，可以有效地分析非线性和非平稳信号。原信号经过经验模式分解(Empirical Mode Decomposition，EMD)被分解为一系列固有模态函数(IMFs)，随后对每个固有模态函数进行希尔伯特黄变换。HHT不涉及海森堡不确定性原理可以获得时域和频域的高分辨率。目前它被广泛应用于许多信号处理领域，如雷达探测，地震信号和生物医学信号等。

再者，由于EEG信号低空间分辨率，EEG信号构成的BCI系统需要进行有效的空间滤波，从而确保从受试的相关脑域中提取特征信息。在这一方面，常用的算法有：共域空间分解(Common Spatial Pattern，CSP)、独立主成分分析(Independent Component Analysis,ICA)和共域空间谱模式(CSSP)、滤波器CSP(Filter Bank Common Spatial Pattern,FBCSP)、判别滤波CSP(Discriminant Filtering Common Spatial Pattern,DFBCSP) 等多种CSP的修改版本。

然而，传统的CSP客观存在着需要大量的输入通道以及缺乏频率信息的不足之处，需要进行改进。

技术实现要素：

本发明目的在于针对传统公共空间模式算法的不足，本发明提出一种公共空间模式算法结合经验模式分解的脑电信号特征提取方法，利用三个通道EMD分解后的固有模态函数进行CSP滤波，在CSP的基础上加入EMD的频域信息，可以很好地解决上述问题，为更好地进行想象运动判别提供了一个可选的途径。

本发明解决上述技术问题所采取的技术方案为一种结合公共空间模式算法和EMD 的脑电信号特征提取方法，具体包括如下步骤：

步骤1：选取若干位受试者的脑电信号作为训练集和测试集，分别对单个受试者的 C3、C4两个通道中的信号进行预处理；

步骤2：对预处理后的EEG信号x(t)进行经验模式分解，得到一系列固有模态函数IMF_i，并绘制所有固有模态函数的能谱图；

步骤3：将单次试验的C3、C4通道前三阶IMF分量合并，构成一个N*T的矩阵X_i， i＝L表示想象左手运动，i＝R表示想象右手运动，其中，N为IMF个数，可看作通道数， T为一次试验的采样点个数，即窗口长度，整个实验过程包含G组试验，共得到G组向量矩阵，分为G1组测试向量矩阵和G2组训练向量矩阵，分别进行公共空间模式分解。

进一步，上述步骤2中，对EEG信号进行经验模式分解的具体步骤如下：

(1)判断每个x(t)的局部极值，用三次样条曲线进行曲线拟合，局部极大值形成上包络e_max(t),局部极小值形成下包络e_min(t)；

(2)求e_max(t)和e_min(t)的均值：

(3)计算输入信号x(t)和m(t)的差值:

c(t)＝x(t)-m(t) (2)；

如果c(t)不能满足IMF的定义截至条件，重复上述过程(1)-(3)，否则，提取c(t)作为固有模态函数，剩余量r(t)计算如下：

r(t)＝x(t)-c(t) (3)；

(4)剩余量作为一个新的数据经过相同的筛选过程以获得下一个更低频率的固有模态函数，直到剩余函数r(t)为一个单调函数或者仅有一个极致时，分解过程停止，假设原始信号x(t)被分解为n个固有模态函数和一个剩余函数量r(t)，可以得重构信号：

进一步，上述公共空间模式分解的算法包括如下步骤：

步骤1：X_L和X_R表示预处理过的EEG矩阵，下标L和R分别代表左右想象运动和右手想象运动，N*T维，N为通道数，T为采样点数，标准化的空间协方差表示为：

步骤2：对复合协方差矩阵进行对角化分解：

白化矩阵：

对平均协方差矩阵进行变形：

S_L和S_R有共同的特征向量，满足下式：

S_L＝B∑_LB^T (11)

S_R＝B∑_RB^T (12)

∑_L+∑_R＝I (13)；

步骤3：成分选择，构造空间滤波器，S_L最大特征值对应的特征向量对应S_R最小特征值，反之亦然，对应白化EEG的最大特征值的特征向量进行变换，可以获得两个信号矩阵的最优分离方差，投影矩阵W表示为：

W＝U^TP (14)

此处W即空间滤波器，原始的EEG信号x(t)经过W可以被投影得到新的数据集 Z₀，如式13所示：

Z₀＝x(t)·W (15)

构建矩阵Z＝[z₁,z₂,…,z_2m]∈R^N×2m由Z₀的前行和后m行构成，特征向量f＝[f₁,f₂,…,f_2m]^T∈R^2m×1即定义为：

其中，该公共空间模式算法的成分选择算法即为通过选择最大的m个特征值和最小的m个特征值所对应的2m个特征向量构造空间滤波器W的过程。

上述成分选择算法的具体步骤如下：

(1)使用对EEG信号进行经验模式分解时采用的结合公共空间模式算法的特征提取过程进行计算，选取所有的特征向量组成空间滤波器W；

(2)记原始输入的M组N*T的矩阵数据为Data1，对Data1用上述滤波器W进行滤波，滤波后的数据为Data2；

(3)计算Data2中六个通道数据的能量，其中包含C3电极前三阶IMF分量和C4 电极前三阶IMF分量，选取每组训练集中不同类别之间能量差异最明显的前三对分量对应的特征向量，构成新的滤波器W′；

(4)选若干组测试数据作为Data3，使用改进后的滤波器W′进行滤波，按照公式 16进行特征提取。

进一步，空间滤波后使用支持向量机进行特征分类，其具体步骤如下：

(1)对于非线性EEG问题，将特征集通过非线性变换转化为另一个空间中的线性问题，构造最优分类面，相应的最优决策函数为：

其中N为支持向量个数，αi为Lagrangue乘子，从而目标函数变为使下式最小化：

核参数γ和误差惩罚因子C是影响SVM性能的主要参数，γ的取值影响空间变换后的数据分布，惩罚因子C则决定了支持向量机的收敛速度及推广能力；因此，对γ和C 的选择很大程度上影响了脑电信号的识别率；

(2)采用网格化交叉验证方法进行γ和C最优参数的选择，将训练集作为原始的数据集，在一定范围内改变核函数和惩罚因子的值，运用交叉验证方法进行分类，选择分类准确率最高的γ和C作为最佳参数；

(3)确定γ和C后，将测试集输入训练好的支持向量机进行特征分类。

作为优选，上述γ和C最优参数可以采用γ＝0.435275，C＝6.9644。

与现有技术相比，本发明的有益效果：

1、本发明利用三个通道EMD分解后的固有模态函数进行CSP滤波，在CSP的基础上加入EMD的频域信息，很好地解决CSP缺乏频域信息的问题。

2、本发明将经验模式分解后的多阶固有模态函数看作多输入信号进行公共空间模式分解，在仅使用C3，C4，Cz三个通道的情况下，获得较好的特征分类结果，解决一般CSP算法需要大量输入通道问题。

3、针对空间滤波器构造做出改进：计算公共空间模式算法滤波后数据在不同类别状态下的能量差异选取空间滤波器的构造成分，构造新的空间滤波器，获取特征向量组，得到更具判别性的特征。

附图说明

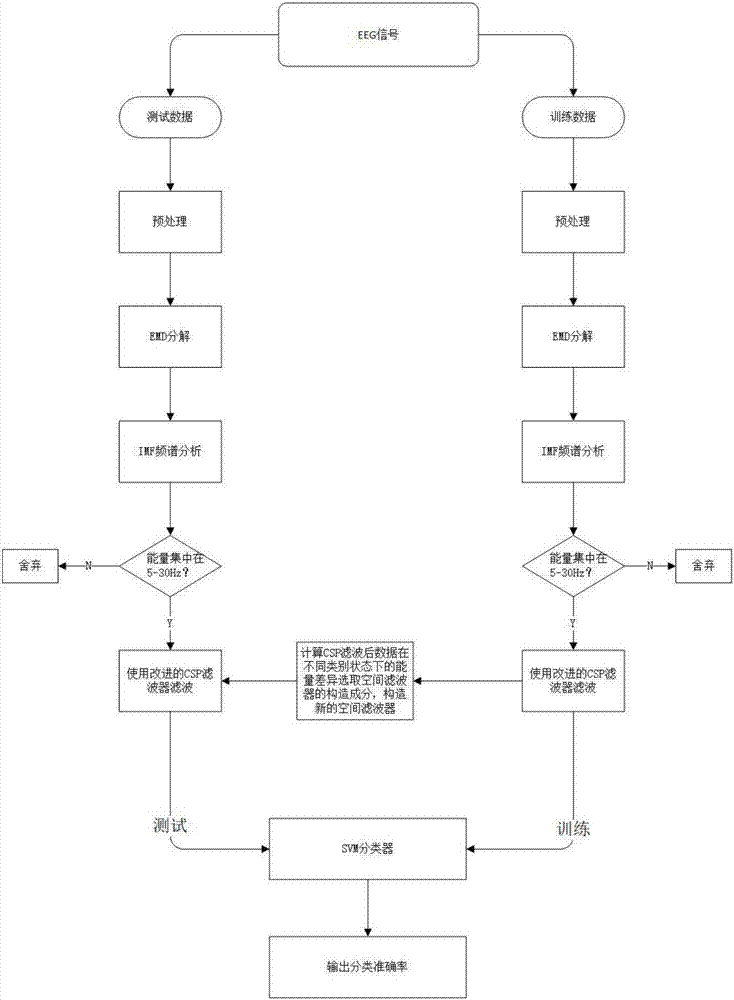
图1为本发明方法流程图。

图2为EEG信号采集流程图。

具体实施方式

下面结合说明书附图对本发明作进一步的详细说明。

本发明主要基于如下内容：1、基于经验模式分解的EEG信号处理；2频域能量分析；3根据频谱分析筛选固有模态函，并进行公共空间模式分解，解决CSP多输入、缺频域信息的问题；4、支持向量机分类。

如图1所示，本发明所述方法包括如下步骤：

步骤1：采集各位受试的脑电信号，信号采集流程如图2所示。选取9位受试的脑电信号作为训练集和测试集，分别对单个受试C3、C4两个通道中的信号进行预处理；包括基线校正、ICA去伪迹、5-30Hz带通滤波；

步骤2：对预处理后的EEG信号x(t)进行经验模式分解；得到一系列固有模态函数IMF_i(i为固有模态函数的阶数)并绘制所有固有模态函数能谱图；

EEG信号进行经验模式分解的具体步骤如下：

(1)判断每个x(t)的局部极值，用三次样条曲线进行曲线拟合，局部极大值形成上包络e_max(t),局部极小值形成下包络e_min(t)。

(2)求e_max(t)和e_min(t)的均值：

(3)计算输入信号x(t)和m(t)的差值:

c(t)＝x(t)-m(t) (2)

如果c(t)不能满足IMF的定义截至条件，重复上述过程(1)-(3)，否则，提取c(t)作为固有模态函数，剩余量r(t)计算如下：

r(t)＝x(t)-c(t) (3)

(4)剩余量作为一个新的数据经过相同的筛选过程以获得下一个更低频率的固有模态函数。直到剩余函数r(t)为一个单调函数或者仅有一个极致时，分解过程停止。假设原始信号x(t)被分解为n个固有模态函数和一个剩余函数量r(t)，可以得重构信号：

步骤3：将次试验的C3，C4通道前三阶IMF分量合并，构成一个6*2000的矩阵X_i(i＝L表示想象左手运动，i＝R表示想象右手运动)，其中，6为IMF个数，可看作通道数，2000为一次试验的采样点个数，即窗口长度。整个实验过程包含120组试验，共得到120组向量矩阵，分为40组测试向量矩阵和80组训练向量矩阵，分别进行公共空间模式分解。

公共空间模式算法包括如下步骤：

(1)X_L和X_R表示预处理过的EEG矩阵(下标L和R分别代表左右想象运动和右手想象运动)，N*T维，N为通道数，T为采样点数。标准化的空间协方差表示为：

(2)对复合协方差矩阵进行对角化分解：

白化矩阵：

对平均协方差矩阵进行变形：

S_L和S_R有共同的特征向量，满足下式：

S_L＝BΣ_LB^T (11)

S_R＝BΣ_RB^T (12)

Σ_L+Σ_R＝I (13)

(3)S_L最大特征值对应的特征向量对应S_R最小特征值，反之亦然。对应白化EEG 的最大特征值的特征向量进行变换，可以获得两个信号矩阵的最优分离方差。投影矩阵W表示为：

W＝U^TP (14)

此处W即空间滤波器，原始的EEG信号x(t)经过W可以被投影得到新的数据集Z₀，如式(13)所示：

Z₀＝x(t)·W (15)

在传统的CSP算法中，构建矩阵Z＝[z₁,z₂,…,z_2m]∈R^N×2m由Z₀的前行和后m行构成，特征向量f＝[f₁,f₂,…,f_2m]^T∈R^2m×1即定义为：

记原始输入数据为Data1，对Data1用上述滤波器W进行滤波，滤波后的数据为 Data2，计算Data2中所有通道(C3电极前三阶IMF分量和C4电极前三阶IMF分量) 数据的能量，选取每组训练集中不同类别之间能量差异最明显的前三对分量对应的特征向量，构成新的滤波器W′；

(4)测试集数据使用改进后的滤波器W′进行滤波，按照公式(16)进行特征提取，从受试01左右手想象运动时单次trial的脑电信号EMD分解后前三阶IMF分量经过CSP空域滤波后特征的脑地形图可见：在进行两类想象运动时，C3、C4电极能量相差较大，同时，想象左手运动和时C4电极明显比C3电极活跃，想象右手运动时则刚好相反，表现为C3电极比C4活跃，这与运动想象中时间按相关同步/去同步特性刚好相符。由此说明，该特征可以有效表征出“源”的空间位置信息，可以作为分类特征。

步骤4：使用支持向量机进行特征分类，其具体步骤如下：

(1)对于非线性EEG问题，将特征集通过非线性变换转化为另一个空间中的线性问题，构造最优分类面。相应的最优决策函数为：

其中N为支持向量个数，αi为Lagrangue乘子。从而目标函数变为使下式最小化：

核参数γ和误差惩罚因子C是影响SVM性能的主要参数。γ的取值影响空间变换后的数据分布，惩罚因子C则决定了支持向量机的收敛速度及推广能力；因此，对γ和 C的选择很大程度上影响了脑电信号的识别率。

(2)采用网格化交叉验证方法进行γ和C最优参数的选择，将训练集作为原始的数据集，在一定范围内改变核函数和惩罚因子的值，运用交叉验证方法进行分类，选择分类准确率最高的γ和C作为最佳参数。

(3)确定γ＝0.435275，C＝6.9644后，将测试集输入训练好的支持向量机进行特征分类。

综上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此。在发明所披露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明所揭露的技术范围之内。因此，本发明的保护范围应以权利要求书的保护范围为准。