铁路钢箱梁桥温度梯度模式评价方法与流程

本发明属于桥梁温度检测技术领域，具体涉及到一种铁路钢箱梁桥温度梯度模式的评价方法。

背景技术：

钢箱梁桥是长期暴露在自然环境中的结构物，在长期的使用过程中必然受到太阳辐射及其周围环境气温等的影响，这些都会影响到桥梁结构的温度分布，产生温度梯度，从而产生温度变形，当钢箱梁桥内外约束阻碍结构的变形时就会产生相当大的温度应力，因此在桥梁结构中的温度效应不容忽视；而研究钢桥结构的温度效应前，首先应对钢桥结构的温度梯度进行研究，给出适合于我国的温度梯度模式。

钢箱梁桥温度荷载形成的根本原因在于太阳能量的传输和地球自身的运动，以及当地气象环境、地理条件。桥梁结构上的温度作用分为均匀温度作用和梯度温度作用。梯度温度作用又可分为竖向温度梯度作用和横向温度梯度作用。温度梯度作用在桥梁结构上会引起温度自约束应力，即结构内部纤维间温度不同，产生的应变差受到纤维间相互约束而引起应力。桥梁结构在日照作用下产生显著温度效应的现象最早于20世纪50年代由前联邦德国学者发现。近几十年来，国内外都发生了由温度应力导致桥梁结构发生严重损坏的事故。

国内外学者对桥梁结构温度作用的早期研究均集中于混凝土桥梁，提出了一系列研究方法并取得了一些研究成果。但随着桥梁结构设计理论的日益成熟与施工技术的发展，大跨度铁路钢箱梁桥的使用日益增加，亟需对铁路钢箱梁桥的温度分布进行规定，以保证铁路钢箱梁桥施工和使用过程中的安全。而我国铁路桥涵设计规范对于铁路钢箱梁桥设计温差标准值尚无明确规定，原因在于得到具有一定重现期的截面温差标准值需要建立在长期广泛的现场实测的基础上，所获得的实测数据数量庞大且后期数据处理工作量巨大。

我国现行的《铁路桥梁钢结构设计规范》对钢梁温度梯度取值没有进行规定。同时，我国现行的《公路桥涵设计通用规范》(jtgd60—2004)规定的温度梯度模式参照美国aashto规范而得，且只给出了铺装后混凝土梁与钢-混组合梁的日照温度梯度。工程设计一般参照英国桥梁规范bs-5400对结构温度效应进行估算，然而，由于各国的日照、气象、地理环境等影响桥梁结构温度分布的外在环境因素的不同，bs-5400温度梯度曲线不一定适用于中国的桥梁结构。因此，在对某铁路钢箱梁进行长期的温度监测之后，对温度数据进行有效的整理分析以得到适用于铁路钢箱梁桥温度梯度模式是非常必要的。

技术实现要素：

本发明所要解决的技术问题在于提供一种铁路钢箱梁桥温度梯度模式评价方法，目的在于得到适用于我国铁路钢箱梁桥的温度梯度模式。

本发明的技术方案是由以下步骤实现的：

(1)在钢箱梁桥腹板和顶板上布置温度测点并采集温度，每次采集时间间隔为2～5分钟；

(2)将采集获得的钢箱梁桥温度进行分析，找出腹板各测点的日极值温差值所对应时刻的温度数据，以温度为横坐标，腹板测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合，得到竖向温度梯度曲线；找出顶板各测点的日极值温差值所对应时刻的温度数据，以温度为横坐标，顶板测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合，得到横向温度梯度曲线；

(3)将得到的温度梯度曲线简化成折线，为温度梯度模式；

(4)得到竖向温度梯度模式腹板各折点的日极值温差值和横向温度梯度模式顶板各折点的日极值温差值；

腹板各折点日极值温差值为各折点处测点温度值减去腹板测点最低温度值，顶板各折点的日极值温差值为顶板各折点处测点温度值减去顶板测点最低温度值；

(5)对钢箱梁桥的顶板和腹板各个折点的日极值温差值进行统计分析，得到温差概率分布直方图，再对直方图进行概率拟合，得到日极值温差概率密度函数；

统计顶板和腹板各个折点的日极值温差值并输入到计算机，应用origin8.0数理统计分析软件分别做出顶板和腹板的各折点的日极值温差值的概率直方图，再分别对顶板和腹板各折点的日极值温差值的概率直方图进行函数拟合，得到对应的概率密度函数f(x)；

(6)通过概率密度函数p0，计算设计基准期为100年，不同重现期n的温差标准值t；

概率密度函数f(x)所对应的分布函数为fx(x)，则设计基准期100年内的顶板和各个折点的极值温差值的累积分布函数fy(x)为：fy(x)＝[fx(x)]¹⁰⁰；

温差标准值的保证率为p0，对铁路钢箱梁桥施工期温度设计标准值进行取值，可将两年作为施工期设计基准期，分别取半年、一年作为施工期温度作用重现期，则施工期内极值温差作用的温差标准值的保证率分别为96％、98％；式中fy(x)为p0，计算得x为温差标准值t；

(7)为方便在实际工程中的应用，对不同重现期无铺装和铺装后铁路钢箱梁的温差标准值进行偏安全取整，得到温差标准值的建议值。

上述的步骤(1)在腹板和顶板上布置温度测点为：两侧腹板布置温度测点位置以距顶板的垂直距离表示为0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板与底板相交处；顶板温度测点布置位置，以距离右侧腹板的水平距离表示为：0.0m，1.4m，2.8m，4.2m。

上述的钢箱梁桥为无铺装钢箱梁桥，无铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝18.7，σ＝3.50，重现期n＝50年，t1＝31.1℃；重现期n＝100年，t1＝31.7℃；施工阶段重现期n＝0.5年，t1＝15.4℃；施工阶段重现期n＝1.0年，t1＝16.2℃；

无铺装钢箱梁桥竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝9.40，σ＝2.91，重现期n＝50年，t2＝19.6℃；重现期n＝100年，t2＝20.2℃；施工阶段重现期n＝0.5年，t2＝15.4℃；施工阶段重现期n＝1.0年，t2＝16.2℃；

无铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝-2.70，σ＝0.68，重现期n＝50年，t1＝-8.5℃；重现期n＝100年，t1＝-9.0℃；施工阶段重现期n＝0.5年，t1＝-5.4℃；施工阶段重现期n＝1.0年，t1＝-5.8℃；

无铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝6.79，σ＝1.18，重现期n＝50年，t1＝11.0℃；重现期n＝100年，t1＝11.2℃；施工阶段重现期n＝0.5年，t1＝9.2℃；施工阶段重现期n＝1.0年，t1＝9.5℃；

无铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-2.32，σ＝1.01，重现期n＝50年，t1＝-5.9℃；重现期n＝100年，t1＝-6.1℃；施工阶段重现期n＝0.5年，t1＝-4.4℃；施工阶段重现期n＝1.0年，t1＝-4.7℃；

上述的钢箱梁桥为混凝土铺装层钢箱梁桥，混凝土铺装层钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝5.13，σ＝3.50，重现期n＝50年，t1＝15.8℃；重现期n＝100年，t1＝16.0℃；施工阶段重现期n＝0.5年，t1＝12.3℃；施工阶段重现期n＝1.0年，t1＝13.3℃；

混凝土铺装层钢箱梁桥竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝3.30，σ＝1.00，重现期n＝50年，t2＝6.8℃；重现期n＝100年，t2＝7.0℃；施工阶段重现期n＝0.5年，t2＝5.4℃；施工阶段重现期n＝1.0年，t2＝5.6℃；

混凝土铺装层钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝-1.26，σ＝0.62，重现期n＝50年，t1＝-6.5℃；重现期n＝100年，t1＝-7.0℃；施工阶段重现期n＝0.5年，t1＝-3.7℃；施工阶段重现期n＝1.0年，t1＝-4.1℃；

混凝土铺装层钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝2.56，σ＝0.88，重现期n＝50年，t1＝5.7℃；重现期n＝100年，t1＝5.8℃；施工阶段重现期n＝0.5年，t1＝4.4℃；施工阶段重现期n＝1.0年，t1＝4.6℃；

混凝土铺装层钢箱梁桥横向温度梯度模式中腹板顶部日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-1.46，σ＝0.85，重现期n＝50年，t1＝-4.5℃；重现期n＝100年，t1＝-4.6℃；施工阶段重现期n＝0.5年，t1＝-3.2℃；施工阶段重现期n＝1.0年，t1＝-3.5℃；

5、根据权利要求1或2所述的铁路钢箱梁桥温度梯度模式评价方法，其特征在于：所述的钢箱梁桥为道砟铺装层钢箱梁桥，道砟铺装层钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝2.58，σ＝1.17，重现期n＝50年，t1＝12.5℃；重现期n＝100年，t1＝13.4℃；施工阶段重现期n＝0.5年，t1＝7.1℃；施工阶段重现期n＝1.0年，t1＝8.0℃；

道砟铺装层钢箱梁桥竖向温度梯度模式中距腹板顶部0.05m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝2.20，σ＝1.35，重现期n＝50年，t2＝6.9℃；重现期n＝100年，t2＝7.2℃；施工阶段重现期n＝0.5年，t2＝5.0℃；施工阶段重现期n＝1.0年，t2＝5.3℃；

道砟铺装层钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-2.52，σ＝2.24，重现期n＝50年，t1＝-9.0℃；重现期n＝100年，t1＝-9.2℃；施工阶段重现期n＝0.5年，t1＝-7.1℃；施工阶段重现期n＝1.0年，t1＝-7.7℃；

道砟铺装层钢箱梁桥横向温度梯度模式中在距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝1.00，σ＝0.70，重现期n＝50年，t1＝3.5℃；重现期n＝100年，t1＝3.6℃；施工阶段重现期n＝0.5年，t1＝2.5℃；施工阶段重现期n＝1.0年，t1＝2.6℃；

道砟铺装层钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-1.87，σ＝0.94，重现期n＝50年，t1＝-5.2℃；重现期n＝100年，t1＝-5.4℃；施工阶段重现期n＝0.5年，t1＝-3.8℃；施工阶段重现期n＝1.0年，t1＝-4.1℃；

道砟铺装层钢箱梁桥横向温度梯度模式中腹板顶部日极值负温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝-0.60，σ＝0.33，重现期n＝50年，t1＝-1.7℃；重现期n＝100年，t1＝-1.8℃；施工阶段重现期n＝0.5年，t1＝-1.3℃；施工阶段重现期n＝1.0年，t1＝-1.4℃。

本发明基于对某铁路钢箱梁现场温度监测数据的分析，提出无铺装、混凝土铺装和道砟铺装钢箱梁横向和竖向温度梯度模式，并通过对现场温度监测数据的日极值温差进行数理统计分析，得到不同铺装铁路钢箱梁在不同重现期下横向和竖向的温差标准值，可用于计算铁路钢箱梁不同施工阶段温度梯度产生的附加应力和变形，保障安全施工和正常运营，为完善我国相关设计规范提供依据。

附图说明

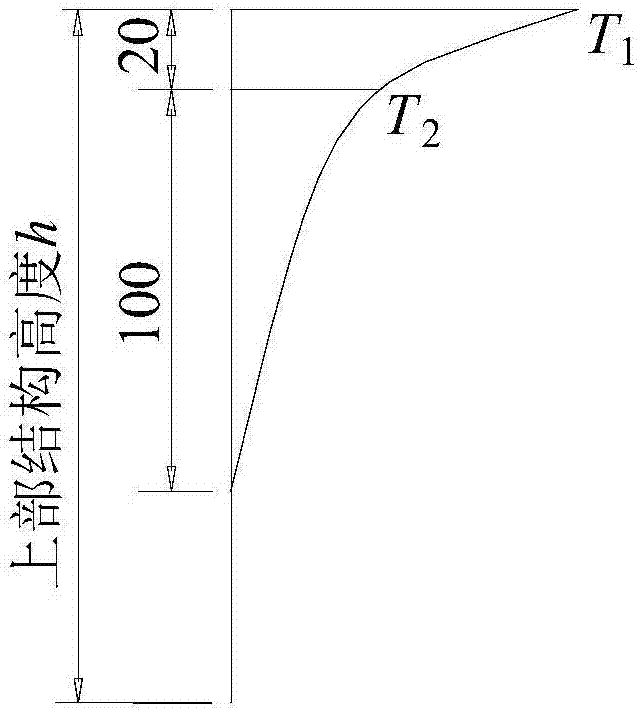
图1是无铺装钢箱梁桥腹板竖向正温度梯度曲线图。

图2是无铺装钢箱梁桥腹板竖向负温度梯度曲线图。

图3是无铺装钢箱梁桥腹板竖向正温度梯度图。

图4是无铺装钢箱梁桥腹板竖向负温度梯度图。

图5是无铺装钢箱梁桥腹板横向正温度梯度曲线图。

图6是无铺装钢箱梁桥腹板横向负温度梯度曲线图。

图7是混凝土铺装钢箱梁桥腹板竖向正温度梯度曲线图。

图8是混凝土铺装钢箱梁桥腹板竖向负温度梯度曲线图。

图9是混凝土铺装钢箱梁桥腹板竖向正温度梯度图。

图10是混凝土铺装钢箱梁桥腹板竖向负温度梯度图。

图11是混凝土铺装钢箱梁桥腹板横向正温度梯度曲线图。

图12是混凝土铺装钢箱梁桥腹板横向负温度梯度曲线图。

图13是道砟层铺装钢箱梁桥腹板竖向正温度梯度曲线图。

图14是道砟层铺装钢箱梁桥腹板竖向负温度梯度曲线图。

图15是道砟层铺装钢箱梁桥腹板竖向正温度梯度图。

图16是道砟层铺装钢箱梁桥腹板竖向负温度梯度图。

图17是道砟层铺装钢箱梁桥腹板横向正温度梯度曲线图。

图18是道砟层铺装钢箱梁桥腹板横向负温度梯度曲线图。

图19是无铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1的概率直方图。

图20是无铺装钢箱梁桥竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2的概率直方图。

图21是无铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1的概率直方图。

图22是无铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1的概率直方图。

图23是无铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1的概率直方图。

图24是混凝土铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1的概率直方图。

图25是混凝土铺装钢箱梁桥竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2的概率直方图。

图26是混凝土铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1的概率直方图。

图27是混凝土铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1的概率直方图。

图28是混凝土铺装钢箱梁桥横向温度梯度模式中腹板顶部日极值负温差标准值t1的概率直方图。

图29是道砟层铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值正温差标准值t1的概率直方图。

图30是道砟层铺装钢箱梁桥竖向温度梯度模式中距腹板顶部0.05m处折点日极值正温差标准值t2的概率直方图。

图31是道砟层铺装钢箱梁桥竖向温度梯度模式中腹板顶部日极值负温差标准值t1的概率直方图。

图32是道砟层铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1的概率直方图。

图33是道砟层铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1的概率直方图。

图34是道砟层铺装钢箱梁桥横向温度梯度模式中腹板顶部日极值负温差标准值t2的概率直方图。

具体实施方式

下面结合附图和实施例对本发明进一步详细说明，但本发明不限于下述的实施方式。

实施例1

1、在无铺装钢箱梁桥腹板和顶板上布置温度测点并采集温度，每次采集时间间隔为3分钟，每次采集时间间隔也可为2分钟，每次采集时间间隔还可为5分钟；

参照英国规范bs-5400对钢桥温度梯度的规定，在无铺装层钢箱梁两侧腹板布置温度测点，温度测点位置以距顶板的垂直距离表示为0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板与底板相交处；在顶板布置温度测点，温度测点位置以距离右侧腹板的水平距离表示为：0.0m，1.4m，2.8m，4.2m；每隔3分钟采集一次各测点温度并记录。

2、将采集获得的无铺装层钢箱梁桥温度进行分析，找出腹板各测点日极值温差值所对应时刻的温度数据，以温度为横坐标，测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合，得到竖向温度梯度曲线；找出混凝土顶板各测点的日极值温差值所对应时刻的温度数据，以温度为横坐标，混凝土顶板测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合，得到横向温度梯度曲线；

在距腹板顶部1.2m内采用非线性拟合，在距顶板1.2m到腹板底部范围内采用线性拟合，得到竖向正温度梯度曲线，如图1所示；在距腹板顶部1.2m范围内采用非线性拟合，在距腹板顶部1.2m至腹板底部范围内采用线性拟合，得到竖向负温度梯度曲线，如图2所示；顶板上距右侧腹板1.4m至2.8m处的温度较高采用线性拟合，距右侧腹板0.0m处测点和4.2m处测点的温度较低且相近，得到呈梯形的横向正温度梯度曲线如图5所示；顶板上距右侧腹板1.4m至2.8m处的温度较低采用线性拟合，距右侧腹板0.0m处测点和4.2m处测点的温度较高且相近，得到呈倒梯形的横向负温度梯度曲线如图6所示。

3、将得到的温度梯度曲线简化成折线，为温度梯度模式；

对竖向正温度梯度曲线简化，在距腹板顶部0.2m内采用直线简化，在距腹板顶部0.2m到1.2m范围内采用直线简化，0.2m处为折点，得到竖向正温度梯度模式如图3所示；

对竖向负梯度曲线简化，在距腹板顶部1.2m内采用直线简化，1.2m处为折点，得到竖向负温度梯度模式如图4所示；

横向正负温度梯度曲线均为折线形，不需要简化。

4、得到竖向温度梯度模式腹板各折点的日极值温差值和横向温度梯度模式顶板各折点的日极值温差值；

腹板各折点日极值温差值为各折点处测点温度值减去腹板测点最低温度值，顶板各折点的日极值温差值为顶板各折点处测点温度值减去顶板测点最低温度值；

5、对钢箱梁桥的顶板和腹板各个折点的日极值温差值进行统计分析，得到温差概率分布直方图，再对直方图进行概率拟合，得到日极值温差概率密度函数；

统计顶板和腹板各个折点的日极值温差值并输入到计算机，应用origin8.0数理统计分析软件分别做出顶板和腹板各个折点的日极值温差值的概率直方图，再分别对顶板和腹板各个折点的日极值温差值的概率直方图进行函数拟合，得到对应的概率密度函数f(x)：

竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝18.7，σ＝3.50，如图19所示；

竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝9.40，σ＝2.91，如图20所示；

竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝-2.70，σ＝0.68，如图21所示；

横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝6.79，σ＝1.18，如图22所示；

无铺装钢箱梁桥横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-2.32，σ＝1.01，如图23所示；

6、通过概率密度函数f(x)，计算设计基准期为100年，不同重现期n的温差标准值t。

概率密度函数f(x)所对应的分布函数为fx(x)，则设计基准期100年内的顶板和各个折点的极值温差值的累积分布函数fy(x)为：fy(x)＝[fx(x)]¹⁰⁰；

温差标准值的保证率为p0，对铁路钢箱梁桥施工期温度设计标准值进行取值，可将两年作为施工期设计基准期，分别取半年、一年作为施工期温度作用重现期，则施工期内极值温差作用的温差标准值的保证率分别为96％、98％；令fy(x)＝p0，计算得x为温差标准值t。

无铺装钢箱梁竖向温差标准值见表1，横向温差标准值见表2。

7、为方便在实际工程中的应用，对不同重现期无铺装铁路钢箱梁的温差标准值进行偏安全取整，得到温差标准值的建议值。

无铺装铁路钢箱梁竖向温差标准值的建议值见表3，横向温差标准值的建议值见表4。

实施例2

1、在混凝土铺装钢箱梁桥腹板和顶板上布置温度测点并采集温度，每次采集时间间隔为3分钟；每次采集时间间隔也可为2分钟，每次采集时间间隔还可为5分钟；

参照英国规范bs-5400对钢桥温度梯度的规定，在混凝土铺装层钢箱梁两侧腹板布置温度测点，温度测点位置以距顶板的垂直距离表示为0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板底部；在顶板布置温度测点，温度测点位置以距离右侧腹板的水平距离表示为：0.0m，1.4m，2.8m，4.2m；每隔3分钟采集一次各测点温度并记录。

2、将采集获得的混凝土铺装层钢箱梁桥温度进行分析，找出腹板各测点日极值温差值所对应时刻的温度数据，以温度为横坐标，测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合。

在距腹板顶部1.2m内采用非线性拟合，在距顶板1.2m到腹板底部范围内采用线性拟合，得到竖向正温度梯度曲线，如图7所示；在距腹板顶部2.4m范围内采用非线性拟合，得到竖向负温度梯度曲线，如图8所示；顶板上距右侧腹板1.4m至2.8m处的温度较高采用线性拟合，距右侧腹板0.0m处测点和4.2m处测点的温度较低且相近，得到呈梯形的横向正温度梯度曲线如图11所示；顶板与阴面腹板的交点处温度最低，顶板与阳面腹板交点处温度最高，得到呈线性分布的横向负温度梯度曲线如图12所示。

3、将得到的温度梯度曲线简化成折线，为温度梯度模式；

对竖向正温度梯度曲线简化，在距腹板顶部0.2m内采用直线简化，在距腹板顶部0.2m到2.4m范围内采用直线简化，0.2m处为折点，得到竖向正温度梯度模式如图9所示；

对竖向负梯度曲线简化，在距腹板顶部2.4m内采用直线简化，得到竖向负温度梯度模式如图10所示；

横向正负温度梯度曲线均为折线形，不需要简化。

4、得到竖向温度梯度模式腹板各折点的日极值温差值和横向温度梯度模式顶板各折点的日极值温差值；

腹板各折点日极值温差值为各折点处测点温度值减去腹板测点最低温度值，顶板各折点的日极值温差值为顶板各折点处测点温度值减去顶板测点最低温度值；

5、对钢箱梁桥的顶板和腹板各个折点的日极值温差值进行统计分析，得到温差概率分布直方图，再对直方图进行概率拟合，得到日极值温差概率密度函数；

统计顶板和腹板各个折点的日极值温差值并输入到计算机，应用origin8.0数理统计分析软件分别做出顶板和腹板各个折点的日极值温差值的概率直方图，再分别对顶板和腹板各个折点的日极值温差值的概率直方图进行函数拟合，得到对应的概率密度函数f(x)：

竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝5.13，σ＝3.50，如图24所示；

竖向温度梯度模式中距腹板顶部0.2m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝3.30，σ＝1.00，如图25所示；

竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝-1.26，σ＝0.62，如图26所示；

横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝2.56，σ＝0.88，如图27所示；

横向温度梯度模式中腹板顶部日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-1.46，σ＝0.85，如图28所示；

6、通过概率密度函数f(x)，计算设计基准期为100年，不同重现期n的温差标准值t。

概率密度函数f(x)所对应的分布函数为fx(x)，则设计基准期100年内的顶板和各个折点的极值温差值的累积分布函数fy(x)为：fy(x)＝[fx(x)]¹⁰⁰；

温差标准值的保证率为p0，对铁路钢箱梁桥施工期温度设计标准值进行取值，可将两年作为施工期设计基准期，分别取半年、一年作为施工期温度作用重现期，则施工期内极值温差作用的温差标准值的保证率分别为96％、98％；

令fy(x)＝p0，计算得x为温差标准值t。

混凝土铺装钢箱梁竖向温差标准值见表1，横向温差标准值见表2。

7、为方便在实际工程中的应用，对不同重现期混凝土铺装铁路钢箱梁的温差标准值进行偏安全取整，得到温差标准值的建议值。

混凝土铺装铁路钢箱梁竖向温差标准值的建议值见表3，横向温差标准值的建议值见表4。

实施例3

1、在道砟层铺装钢箱梁桥腹板和顶板上布置温度测点并采集温度，每次采集时间间隔为3分钟；每次采集时间间隔也可为2分钟，每次采集时间间隔还可为5分钟；

参照英国规范bs-5400对钢桥温度梯度的规定，在道砟铺装层钢箱梁两侧腹板布置温度测点，温度测点位置以距顶板的垂直距离表示为0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板底部；在顶板布置温度测点，温度测点位置以距离右侧腹板的水平距离表示为：0.0m，1.4m，2.8m，4.2m；每隔3分钟采集一次各测点温度并记录。

2、将采集获得的混凝土铺装层钢箱梁桥温度进行分析，找出腹板各测点日极值温差值所对应时刻的温度数据，以温度为横坐标，测点间的距离为纵坐标，作出梯度散点图，并采用最小二乘法进行曲线拟合。

在距腹板顶部2.4m范围内采用非线性拟合，得到竖向正温度梯度曲线，如图13所示；在距腹板顶部2.4m范围内采用非线性拟合，得到竖向负温度梯度曲线，如图14所示；顶板上距右侧腹板1.4m至2.8m处的温度较高采用线性拟合，距右侧腹板0.0m处测点和4.2m处测点的温度较低且相近，得到呈梯形的横向正温度梯度曲线，如图17所示；顶板上距右侧腹板1.4m至2.8m处的温度较低采用线性拟合，顶板与阴面腹板相交处温度次之，顶板与阳面腹板相交处温度最高，得到呈线性的横向负温度梯度曲线，如图18所示。

3、将得到的温度梯度曲线简化成折线，为温度梯度模式；

对竖向正温度梯度曲线简化，在距腹板顶部0.05m范围内采用直线简化，在距腹板顶部0.05m到2.4m范围内采用直线简化，0.05m处为折点，得到竖向正温度梯度模式如图15所示；

对竖向负梯度曲线简化，在距腹板顶部2.4m范围内采用直线简化，得到竖向负温度梯度模式如图16所示；

横向正负温度梯度曲线均为折线形，不需要简化。

4、得到竖向温度梯度模式腹板各折点的日极值温差值和横向温度梯度模式顶板各折点的日极值温差值；

腹板各折点日极值温差值为各折点处测点温度值减去腹板测点最低温度值，顶板各折点的日极值温差值为顶板各折点处测点温度值减去顶板测点最低温度值；

5、对钢箱梁桥的顶板和腹板各个折点的日极值温差值进行统计分析，得到温差概率分布直方图，再对直方图进行概率拟合，得到日极值温差概率密度函数；

统计顶板和腹板各个折点的日极值温差值并输入到计算机，应用origin8.0数理统计分析软件分别做出顶板和腹板各个折点的日极值温差值的概率直方图，再分别对顶板和腹板各个折点的日极值温差值的概率直方图进行函数拟合，得到对应的概率密度函数f(x)：

竖向温度梯度模式中腹板顶部日极值正温差标准值t1符合极值ⅰ型分布，其概率密度函数为：

式中μ＝2.58，σ＝1.17，如图29所示；

竖向温度梯度模式中距腹板顶部0.05m处折点日极值正温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝2.20，σ＝1.35，如图30所示；

竖向温度梯度模式中腹板顶部日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-2.52，σ＝2.24，如图31所示；

横向温度梯度模式中距两侧腹板1.4m处日极值正温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝1.00，σ＝0.70，如图32所示；

横向温度梯度模式中距两侧腹板1.4m处日极值负温差标准值t1符合正态分布，其概率密度函数为：

式中μ＝-1.87，σ＝0.94，如图33所示；

横向温度梯度模式中腹板顶部日极值负温差标准值t2符合正态分布，其概率密度函数为：

式中μ＝-0.60，σ＝0.33，如图34所示；

6、通过概率密度函数f(x)，计算设计基准期为100年，不同重现期n的温差标准值t；

概率密度函数f(x)所对应的分布函数为fx(x)，则设计基准期100年内的顶板和各个折点的极值温差值的累积分布函数fy(x)为：fy(x)＝[fx(x)]¹⁰⁰

温差标准值的保证率为p0，对铁路钢箱梁桥施工期温度设计标准值进行取值，可将两年作为施工期设计基准期，分别取半年、一年作为施工期温度作用重现期，则施工期内极值温差作用的温差标准值的保证率分别为96％、98％；

令fy(x)＝p0，计算得x为温差标准值t。

道砟层铺装钢箱梁竖向温差标准值见表1，横向温差标准值见表2。

7、为方便在实际工程中的应用，对不同重现期道砟层铺装铁路钢箱梁的温差标准值进行偏安全取整，得到温差标准值的建议值。

道砟层铺装铁路钢箱梁竖向温差标准值的建议值见表3，横向温差标准值的建议值见表4。

表1铁路钢箱梁竖向温差标准值

表2铁路钢箱梁横向温差标准值

表3铁路钢箱梁竖向温差标准值的建议值

表4铁路钢箱梁横向温差标准值的建议值