一种机车自动驾驶控制预测模型机器学习方法与流程

本发明涉及铁路运输调度领域，尤其是一种涉及机车自动驾驶控制预测模型机器学习方法。

背景技术：

机车自动驾驶优化控制是机车自动控制系统的核心功能之一，其主要作用是根据最优速度曲线轨迹，基于实际运动状态并结合跟随控制算法计算得到相应的控制输入量，并将该控制输入量作用于机车完成速度控制的实际操作过程。

机车自动驾驶系统需要实现准点、舒适和节能运行等指标。最优速度曲线的优化生成是机车自动驾驶系统满足准点、舒适和节能等指标的保证，也是进行机车驾驶控制的依据。但在实际运行过程中，因为各种外部因素的影响，机车的实际运行轨迹较难与理想曲线重合，因此机车自动驾驶系统中最优速度曲线跟随控制算法的主要目标是尽可能减少机车实际运行速度曲线与最优速度曲线的误差，以保证机车能够按照最优速度曲线完成运行任务，因此机车自动驾驶系统控制算法是保证机车实现准点、平稳和节能运行的关键技术之一。

预测控制算法是常用的基于模型的控制算法之一，现有预测控制算法需要依赖于描述过程动态行为的预测模型。目前经典的预测模型主要在处理线性系统的预测控制方面有着不错的表现。然而对于一般意义的非线性系统，采用近似的线性模型进行预测控制时，由于偏差大而难以达到优化控制的目标，于是出现了一些针对非线性预测控制研究。

目前针对非线性预测控制研究包括基于机理模型的预测控制，但是机理模型存在部分参数需要实验确定。然而在机车实际运行过程中存在一些因素对于模型预测效果的干扰，容易导致预测的机车实际运行速度曲线的误差增大，因此现有仅仅依靠机理模型的预测控制算法无法准确预测机车实际运行状态。

技术实现要素：

本发明的目的是针对现有技术存在的问题，提供一种机车自动驾驶控制预测模型机器学习方法，其能够准确预测机车实际状态。

本发明的目的通过如下技术方案实现：

本发明提供一种机车自动驾驶控制预测模型机器学习方法，其包括：

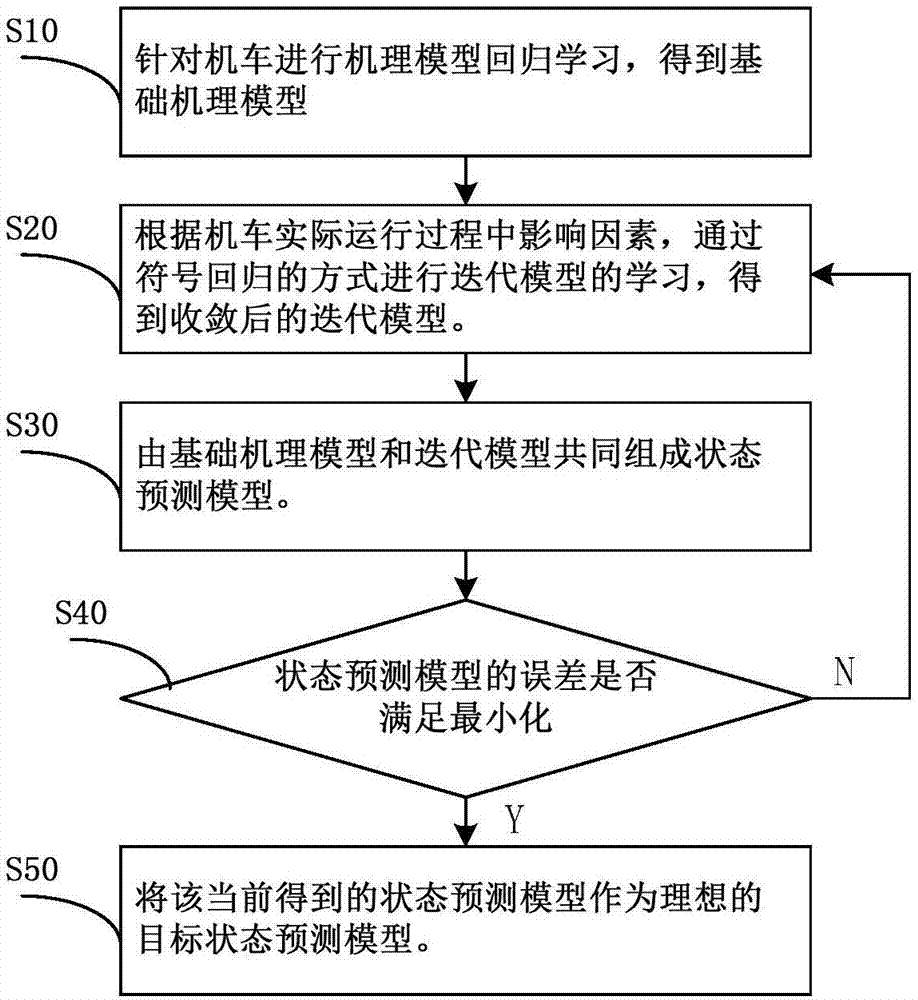
步骤s10，针对机车进行机理模型回归学习，得到基础机理模型；

步骤s20，根据机车实际运行过程中影响因素，通过符号回归的方式进行迭代模型的学习，得到收敛后的迭代模型；

步骤s30，由基础机理模型和迭代模型共同组成状态预测模型；

步骤s40，通过方程选择函数鉴别状态预测模型的误差是否满足最小化，若满足，则执行步骤s50，即将该当前得到的状态预测模型作为理想的目标状态预测模型；若不满足条件，则继续返回步骤s20。

更优选地，所述步骤s10包括：

步骤一，将机车作为研究对象，通过机车的动力学模型，确定机车机理模型；所述机车机理模型，表示如下：

在上述公式中，c表示机车在轨道前进方向的合力；m表示机车的重量；v为机车当前的运行速度；t为机车当前的运行时间；即为当前机车的加速度；s为机车的位置即公里标；f(s)表示当前机车所在位置的牵引力；w为机车运行阻力；b为机车制动装置引起的对机车起到向后作用的制动阻力；

步骤二，根据所确定的机车机理模型，进行机理模型的回归学习，得到基础机理模型。

更优选地，所述步骤二包括：

采用多项式回归方法，对机车机理模型进行机理模型回归学习，得到误差平方和最小时的优化目标函数，并将该优化目标函数作为基础机理模型。

更优选地，所述步骤s20包括：

步骤s201，根据机车状态信息确定函数变量，并结合函数集确定迭代模型的初始种群；

步骤s202，计算种群的适应度值；

根据列车信息、司机信息和线路信息的输入进行状态抽象，利用如下公式计算种群的适应度(种群逼近真实解的近似程度)：

公式中，i表示第i个种群，f(xj)表示第i个种群中第j个个体的计算值,g(x)表示第i个种群中第j个个体的目标值；fi表示第i个种群中第j个个体的适应度值；

步骤s203，判断群体的适应度值是否符合状态转移条件，若满足，则执行步骤s204；若不满足，则执行步骤s206，即在当前种群基础上以设定的概率执行变异、插入、迁移、重组遗传算子，产生新种群，跳转至步骤s202；

步骤s204，结束运算，输出相应的表达式，得到当前状态下最优的调度动作，然后转入步骤s205；

步骤s205，根据当前状态下最优的调度动作执行选择操纵动作，并将改变后的机车状态信息与选择操纵动作等函数变量反馈给迭代模型。

由上述本发明的技术方案可以看出，本发明具有如下技术效果：

本发明结合机车机理模型，采用机器学习的方式学习适用于嵌入式系统且预测精度高的状态预测模型，得到机车自动驾驶控制的目标状态预测模型；通过该目标状态预测模型，使得预测算法的预测精度更高。

附图说明

图1为本发明的实施架构图；

图2为本发明的实施流程图。

具体实施方式

以下将结合附图对本发明的技术方案做进一步详细说明。

实施例一

本发明提供一种机车自动驾驶控制预测模型机器学习方法，其基于机理模型，结合实验数据，采用符号回归的方法进行预测模型的学习。其实施如图1和图2所示，包括如下步骤：

步骤s10，针对机车进行机理模型回归学习，得到基础机理模型。

针对机车进行机理模型回归学习是减小模型误差的方式之一，因此本实施例中首先针对研究对象进行机理模型回归学习得到基础机理模型。

该步骤s10的执行过程具体如下：

一、确定机车机理模型。

将某一机车作为研究对象，通过分析机车的动力学模型的物理原理及计算公式，确定机车机理模型，具体如下：

机车在行驶过程中会受到不同方向和大小的作用力，受力情况复杂，但在通常情况下仅仅考虑机车沿着轨道前进方向的作用力，因此可以确定机车机理模型即为根据机车的受力情况而确定的机车运动方程，表示如下：

在上述公式中，c表示机车在轨道前进方向的合力；m表示机车的重量；v为机车当前的运行速度；t为机车当前的运行时间；即为当前机车的加速度；s为机车的位置即公里标；f(s)表示当前机车所在位置的牵引力；w为机车运行阻力；b为机车制动装置引起的对机车起到向后作用的制动阻力。

上述机车运行阻力w包括两部分：一部分为机车的基本阻力，主要由机车在运行过程中轴承摩擦、车轮滚动等产生的阻力；另一部分为机车在线路坡段、曲线、隧道等运行时产生的附加阻力。因此机车运行阻力w可以通过如下公式计算：

w＝rb(v)+rl(s)(2)

其中，

在上述公式中，v为机车当前的运行速度；rb(v)为机车的基本阻力；s为机车的位置即公里标；rl(s)为当前机车在所在位置运行时产生的附加阻力。

对于机车的基本阻力rb(v)，根据城市轨道交通机车牵引规范，通过以下公式进行计算：

rb(v)＝m(a1+a2v+a3v²)(4)

上式中，v为机车的运行速度；m表示机车的重量；a1，a2，a3为常数系数，需要根据实验确定，随机车车辆类型而异。

附加阻力rl(s)主要是由其所在的线路情况引起，包括坡道附加阻力、曲线附加阻力和隧道附加阻力等。

坡道附加阻力wg为：

wg＝i(n/kn)(5)

式中i为机车所在的坡度值，单位为千分度，该值若为正，则表示上坡；若为负，则表示下坡。

曲线附加阻力wc为：

式中r为机车所在曲线的曲率半径，单位为米；a4表示常数系数，需要根据实验确定，需要根据实验确定。

隧道的附加阻力wt为：

wt＝a5ls(n/kn)(7)

式中ls为隧道的长度，单位为米；a5表示实验系数，需要根据实验确定。

因此机车附加阻力为三者之和，即：

rl(s)＝wg+wc+wt(8)

二、根据所确定的机车机理模型，进行机理模型的回归学习，得到基础机理模型。具体过程如下：

根据以上公式(1)所表示的机车机理模型进行机理模型回归学习时，采用多项式回归方法，优化目标函数即为误差平方和最小时的函数。下面给出多项式回归分析的说明：

设变量y与x的关系为p次多项式，且在xi处对y的随机误差εi服从正态分布，则存在非线性的多项式模型：

公式(9)中，β0、β1.。。βp即为对应项数的系数，εi为随机误差。

令则上述非线性的多项式模型即转化为多元线性模型，即：

yi＝β0+β1xi1+β2xi2+...+βpxip+εi(i＝1，2，…，n)10)

公式(10)中的β0、β1.。。βp即为对应项数的系数，εi为随机误差。

之后采用多元线性回归分析的方法来得到优化目标函数。具体如下：

提取出上述公式(10)的系数矩阵a、结构矩阵x、常数矩阵b，分别为：

上述公式(11)、(12)和(13)中，p为多项式的次数，n为变量y与x的数量。

回归方程系数的最小二乘估计为：

b＝a’b＝(x^tx)^-1xy(14)

则最终得到的误差平方和最小时的函数为优化目标函数，即为基础机理模型。

步骤s20，根据机车实际运行过程中影响因素，通过符号回归的方式进行迭代模型的学习，得到收敛后的迭代模型。

机车实际运行过程中，会有很多因素会对基础机理模型有影响，这些因素如线路信息、机车信息和运行信息等。鉴于实际运行过程中各种因素对基础机理模型的准确性的影响，因此通过符号回归的方式进行迭代模型的学习。

符号回归的过程即函数建模的过程，在此过程中，根据给定一组自变量值和一组函数值(称为训练数据)，找出拟合训练数据的函数关系式。符号回归采用遗传编程(gp)办法，具体执行过程如下：

步骤s201，确定函数变量和函数集，并根据其确定迭代模型的初始种群。

对于符号回归，函数变量包括列车信息、司机信息和线路信息等机车状态信息输入变量，以及调度动作和选择操纵动作等随机变量。函数集包括所需要使用的运算法则。根据上述列车信息、司机信息和线路信息等函数变量和函数集确定出初始种群。

步骤s202，计算种群的适应度值。

根据列车信息、司机信息和线路信息的输入进行状态抽象，利用如下公式计算种群的适应度(种群逼近真实解的近似程度)：

公式中，i表示第i个种群，f(xj)表示第i个种群中第j个个体的计算值,g(x)表示第i个种群中第j个个体的目标值；fi表示第i个种群中第j个个体的适应度值。

步骤s203，判断群体的适应度值是否符合状态转移条件(该状态转移条件可以为连续n代适应度值未变化，也可以为设定的适应度阈值)，若满足，则执行步骤s204；若不满足，则执行步骤s206，即在当前种群基础上以设定的概率执行变异、插入、迁移、重组等遗传算子，使得种群得以进化，根据种群进化结果产生新种群，跳转至步骤s202执行计算该新种群的适应度值。

步骤s204，即结束运算，输出相应的表达式，得到当前状态下最优的调度动作，然后转入步骤s205。

步骤s205，根据当前状态下最优的调度动作执行选择操纵动作，并将改变后的机车状态信息与选择操纵动作等函数变量反馈给迭代模型。

如此不断迭代地进行训练和学习，最终使得迭代模型得以收敛。

步骤s30，由基础机理模型和迭代模型共同组成状态预测模型。

步骤s40，通过方程选择函数鉴别状态预测模型的误差是否满足最小化，若满足，则执行步骤s50，即将该当前得到的状态预测模型作为理想的目标状态预测模型；若不满足条件，则继续返回步骤s20。

方程选择函数中预设了目标误差，以该目标误差为标准，通过方程选择函数鉴别状态预测模型的误差是否满足最小化。

由上述可以看出，本发明结合机车机理模型，采用机器学习的方式学习适用于嵌入式系统且预测精度高的状态预测模型，得到机车自动驾驶控制的目标状态预测模型；通过该机车自动驾驶控制的目标状态预测模型，使得预测算法的预测精度更高。

虽然本发明已以较佳实施例公开如上，但实施例并不限定本发明。在不脱离本发明之精神和范围内，所做的任何等效变化或润饰，同样属于本发明之保护范围。因此本发明的保护范围应当以本申请的权利要求所界定的内容为标准。