一种基于协同昂贵优化算法定位供水管网污染源的方法与流程

本发明涉及定位供水管网污染源的方法，尤其涉及一种基于协同昂贵优化算法定位供水管网污染源的方法。
背景技术：
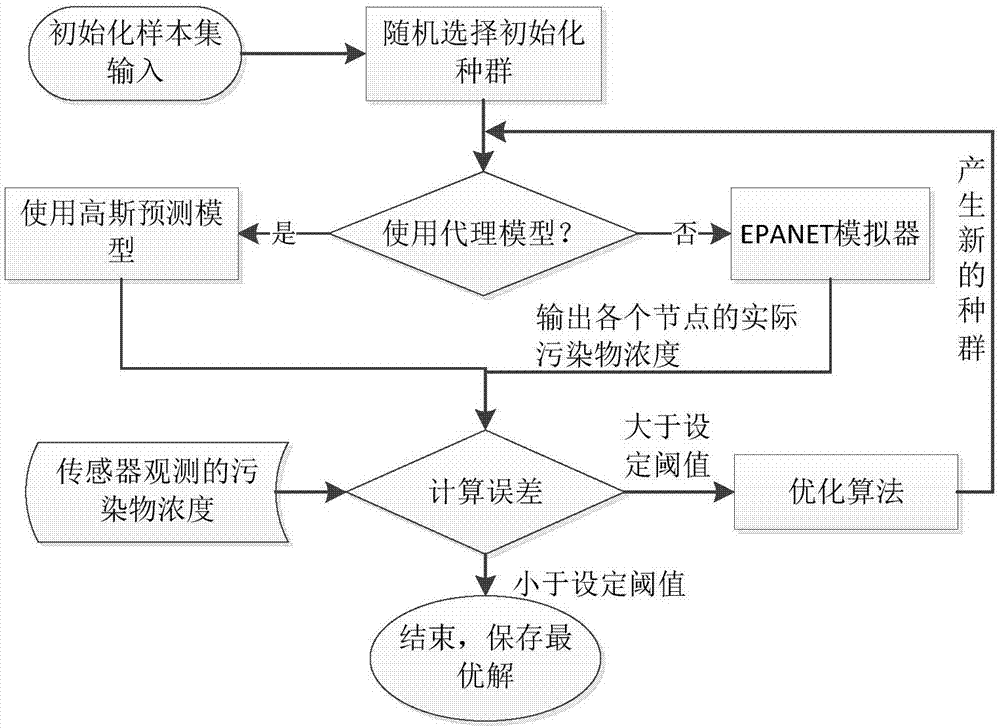
：为了预防水污染事件造成重大灾害及损失，城镇供水管网需要安装配置饮用水安全实时监测系统。在该系统中，通过在关键节点或水源布置水质传感器，可以达到实时监测的目的。当污染事件发生时，如何通过水质传感器采集的信息，对污染源头的特征进行定位，并预测污染物位置、注入时间、注入持续时间和注入质量等信息，是现在急需解决的问题。目前看来，有如下三个主流的方法，粒子追踪法、模拟优化、机器学习的方法。其中的模拟-优化的方法尝试利用模拟-优化模型把污染源定位问题转换优化问题，然后再利用演化计算方法进行优化得到最优解。模拟-优化的方法解决非线性的污染源定位问题，通过不断的读取传感器数据优化预测和校正污染源，最后识别出污染源和污染物释放历史；基于进化算法的自适应动态优化技术来搜索污染源特性(开始时间、位置、释放历史)，通过不断加入新的可用传感器，慢慢收敛得到唯一的最优解。在模拟-优化的方法中，优化算法作为优化器，在优化算法中，每个个体都需要利用网平差软件(epanet)作为模拟器进行仿真模拟污染事件，从而计算适应度值，以管网包含12527个节点，2个水库，2个水池，布置了20个传感器为例(如图1所示)，模拟一次污染源事件，计算适应度值需要耗时将近3秒，当使用遗传算法(种群规模为100，运行100代)进行求解时，耗时329分钟，即将近5.5小时。由此可知，在优化过程中，epanet模拟器消耗大量时间成本，为了尽量减小污染物对公共健康的危害，当获取了一定量水质信息后，需要尽可能快的定位污染源位置，此时进行最优解的搜索的次数将更多，消耗更大的计算成本。也就是说，在较大的供水管网中，采用模拟优化的方法，由于epanet的大量使用，找到污染源的信息，耗时会非常严重。在许多实际的工程优化问题中，目标函数不能用表达式清楚的表示，优化模型也比较复杂，需要使用时间成本大的仿真软件来模拟和进行评价，每一次计算都要耗费高昂的时间代价和经济代价，此类问题称为昂贵优化问题。对于目标函数计算昂贵的优化问题，如果仍然使用一般的优化算法进行求解，在优化算法的寻优过程中需要反复多次迭代，导致大量的昂贵仿真模型的使用，严重影响了算法的性能和效率。昂贵优化方法中，使用计算成本低的代理模型去代替原计算量大的目标函数，得到一个近似解，节省大量的时间。求解昂贵优化问题的关键点在于尽可能的减少昂贵仿真模型的使用同时又不影响算法的求解精度。技术实现要素：有鉴于此，本发明的实施例提供了一种采用了协同算法，根据不同的种群，有针对性的采用不同的策略，有效的改善算法的稳定性的基于协同昂贵优化算法定位供水管网污染源的方法。本发明的实施例提供一种基于协同昂贵优化算法定位供水管网污染源的方法，将供水网管中的污染源定位问题转化为优化问题，然后对优化问题进行求解即定位供水管网污染源，所述优化问题利用昂贵优化算法求解，在所述昂贵优化算法中引入高斯预测模型协同计算。进一步，所述昂贵优化算法中引入高斯预测模型协同计算的具体步骤为：s1.获取供水管网中每个水质传感器检测到的污染物浓度；s2.利用昂贵优化算法随机产生初始化样本集；s3.在步骤s2的初始化样本集中随机选择初始化种群；s4.将步骤s3初始化种群中的每个个体表示一个污染事件，并通过网平差软件模拟器模拟污染事件，输出供水管网各个节点的实际污染物浓度，并将输出供水管网各个节点的实际污染物浓度与步骤s1中检测到的污染物浓度相比较，计算个体适应度值；在保证定位精确度的情况下，通过高斯预测模型预测个体适应度值；s5.若步骤s4得到的个体适应度值小于设定阈值，则结束，保存最优解；若步骤s4得到的个体适应度值大于设定阈值，则优化算法至求得最优解。进一步，所述步骤s5中，优化算法包括以下步骤：s5.1.将初始化种群p根据污染源的位置、注入时间和注入质量均匀划分为三个子种群，分别为pl、pt、pm；s5.2.对子种群pl、pt、pm均采用改进轮盘赌选择；s5.3.对子种群pl采用交叉算子和变异算子进行处理；对子种群pt采用交叉算子和邻近搜索策略进行处理；对子种群pm采用交叉算子和改进的变异策略进行处理；s5.4.步骤s5.3中针对交叉算子和变异算子产生的新个体采用高斯预测模型预测个体适应度值μ和预测误差σ，如果触发系数3σ/μ＜0.2直接使用高斯预测模型预测个体适应度值μ作为新个体适应度值，否则，随机生成一个概率p*，如果p*＜p,p＝t/x使用网平差软件计算个体适应度值，其中，t表示迭代次数，x为基数，否则，使用高斯预测模型预测个体适应度值；s5.5.在每一次迭代结束后，种群根据个体适应度值进行排序，对高斯预测模型预测的个体适应度值的前n个个体使用网平差软件重新计算个体适应度值进行校正，n为种群的10％；s5.6.对经过步骤s5.5处理的子种群pl、pt、pm分别使用精英策略，在pl种群中精英个体出现相同的情况下，采用扰动策略，在pm中对于每一精英个体直接使用扰动策略；s5.7.经过s代的整数倍，子种群pl、pt、pm把最优个体的对应基因相互组合产生新的个体，并均匀加入的子种群pl、pt、pm直接替换对应的最差个体；s5.8.达到最大迭代次数，则结束。进一步，所述高斯预测模型基于高斯随机过程建模，高斯随机过程建模模拟的参数少，并通过最大似然概率和优化算法求解。进一步，所述步骤s5.2中，改进轮盘赌选择方法具体如下：针对种群p，采用基本的轮盘赌选择得到新种群np；统计新种群np中污染源位置相同个体出现的次数；对相同污染源位置出现次数大于或等于n次的个体保留其中适应度最好的个体npi复制到种群pi中，n根据实验经验值得出，而余下的n-1个个体不进行复制，相应位置的种群p保留；若污染源位置出现次数小于n，直接将np中个体复制的到种群p中相应的位置。进一步，所述精英策略中精英个体出现相同的情况时，对相同精英个体进行扰动，即在位置上去搜索供水管网拓扑结构相近的节点，当出现有更好的个体时替换相同的精英个体，没有更好个体时，则直接选用种群中不一样的仅次于相同精英个体的个体。进一步，所述邻近搜索策略把开始时间和持续时间看做一个整体，每次迭代中，所述开始时间和持续时间共同决定一个时间序列，搜索和开始时间和持续时间共同决定的时间序列重合程度最高的时间序列。进一步，所述改进的变异策略为结合粒子群优化算法的思想，去向着最好的个体变异，且加入了一个自适应因子，来保证个体的多样性，改进的变异策略的算法在运行过程中，自适应因子会随着算法的收敛，逐渐变小，使得变异的范围能够自适应的调整。进一步，所述自适应因子的公式为：individual(ij)＝(individual(ij)+bestindividual(ij))/2+rand*maxdistance式中：individaul表示个体，i表示需要进行突变的序号，即表示维度，bestindividual表示的是pm种群中的最好的个体，rand表示(0，1)之间的随机数，maxdistance表示在第j维中所有个体的最大间距。与现有技术相比，本发明具有以下有益效果：基于经典的昂贵优化求解过程，在优化算法的收敛过程中引入高斯预测模型来减少真实评价函数的使用次数。在优化过程中，不断调整策略，平衡高斯预测模型与epanet模拟器的使用，使算法在达到所需精确度的同时减少epanet模拟器的使用次数。协同算法中的合作型协同进化算法采用一种“分而治之”的思想，把复杂的问题分解成多个子问题，然后对各个子问题分别求解，种群之间相互交流，合作实现协同优化。协同算法中的分布式进化算法，是通过不同子种群分别协同搜索，并且经过种群迁移实现信息的共享。不同种群之间可以使用不同的策略、算法来实现共同进化。合并两者的特点，在把问题分解的同时，结合污染源这一具体问题的特性，采用不同的策略，有针对性的搜索不同含义的变量空间。划分为三个子种群，分别为location、time、mass种群。它们拥有相同的决策变量，只是搜索空间有所不同。也就是说各个种群只是搜索对应的决策空间(有下划线的)，而其他的决策空间(不带下划线的)不改变。在各自搜索一定迭代次数后，种群之间相互交流，共享信息。附图说明图1是供水管网的局部放大图。图2是本发明一种基于协同昂贵优化算法定位供水管网污染源的方法的一流程图。图3是图2中优化算法的一流程图。图4是本发明中基于高斯随机过程的建模示意图。图5是使用一次高斯代理模型预测和使用一次epanet模拟器计算个体适应度值所需的时间对比图。图6是使用高斯代理模型与不使用高斯代理模型的算法的epanet使用次数与消耗时间对比图。图7是本发明实验结果示意图。具体实施方式为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式作进一步地描述。本发明的实施例提供了一种基于协同昂贵优化算法定位供水管网污染源的方法，将供水网管中的污染源定位问题转化为优化问题，然后对优化问题进行求解即定位供水管网污染源，所述优化问题利用昂贵优化算法求解，在所述昂贵优化算法中引入高斯预测模型协同计算。从优化的角度来看，当污染事件在传感器处的累积模拟浓度和实际累积检测浓度最小方差为0或小于某一阈值ε时，则认为该污染事件注入的节点就是实际的污染源。优化问题可以表述为：s.t.m＝{m1,m2,…,mk}；mi≥0n∈{1,n}ti≤ts这里，n是管网的节点总数，ns表示传感器的数目，ts表示仿真周期，m表示污染物注入向量，n表示污染源注入的管网节点序号，ti表示注入污染物的初始时间，cj(t)表示在时间t时传感器j的污染物浓度，它是(m,n,ti)的函数，cj*(t)表示在时间t时传感器j的实际检测的污染物浓度。优化的目标即求(m,n,ti)使得方差最小。利用模拟-优化模型求解污染源定位问题时，epanet作为模拟器，优化算法作为优化器，与一般的模拟-优化模型不同的是计算个体适应度值时使用epanet模拟器还是高斯预测模型，而在优化算法中引入高斯预测模型可以减少epanet模拟器的使用次数，提高算法的效率，基于昂贵优化算法的求解框架如图2所示，在昂贵优化算法里，采用高斯随机过程建模，遗传算法作为优化算法，种群中每个个体表示一个污染事件，可以通过epanet模拟器模拟污染事件，输出管网节点实际的污染物浓度信息，通过与传感器实际检测的信息比较，计算个体的适应度值，也可以采用高斯预测模型预测个体适应度值。通过合理平衡epanet和高斯预测模型的使用，可以在保证定位精确度的情况下，尽可能少的使用epanet模拟器，减少算法的时间成本。基于高斯随机过程建模：由于预测模拟对个体的评价有着最直接的影响，所以，合适的预测模型是昂贵优化问题的关键；高斯随机过程建模是一种建立代理模型的方法，高斯随机过程模拟的参数少并且通过最大似然概率和优化算法方便求解。根据供水管网的节点间特性，提出针对供水管网的每个节点建立一个子模型，如图4所示。昂贵优化算法中引入高斯预测模型协同计算的具体步骤为：s1.获取供水管网中每个水质传感器检测到的污染物浓度；s2.利用昂贵优化算法随机产生初始化样本集；s3.在步骤s2的初始化样本集中随机选择初始化种群；s4.将步骤s3初始化种群中的每个个体表示一个污染事件，并通过网平差软件模拟器模拟污染事件，输出供水管网各个节点的实际污染物浓度，并将输出供水管网各个节点的实际污染物浓度与步骤s1中检测到的污染物浓度相比较，计算个体适应度值；在保证定位精确度的情况下，通过高斯预测模型预测个体适应度值；s5.若步骤s4得到的个体适应度值小于设定阈值，则结束，保存最优解；若步骤s4得到的个体适应度值大于设定阈值，则优化算法至求得最优解。基于经典的昂贵优化求解过程，在优化算法的收敛过程中引入高斯预测模型来减少真实评价函数的使用次数。在优化过程中，不断调整策略，平衡高斯预测模型与epanet模拟器的使用，使算法在达到所需精确度的同时减少epanet模拟器的使用次数。协同算法中的合作型协同进化算法采用一种“分而治之”的思想，把复杂的问题分解成多个子问题，然后对各个子问题分别求解，种群之间相互交流，合作实现协同优化；协同算法中的分布式进化算法，是通过不同子种群分别协同搜索，并且经过种群迁移实现信息的共享。不同种群之间可以使用不同的策略、算法来实现共同进化。因此，合并两者的特点，在把问题分解的同时，结合污染源这一具体问题的特性，采用不同的策略，有针对性的搜索不同含义的变量空间。划分为三个子种群，分别为location、time、mass种群。它们拥有相同的决策变量，只是搜索空间有所不同。也就是说各个种群只是搜索对应的决策空间(有下划线的)，而其他的决策空间(不带下划线的)不改变。在各自搜索一定迭代次数后，种群之间相互交流，共享信息。如图3所示，优化算法包括以下步骤：s5.1.将初始化种群p根据污染源的位置、注入时间和注入质量均匀划分为三个子种群，分别为pl、pt、pm；s5.2.对子种群pl、pt、pm均采用改进轮盘赌选择；由于供水管网的复杂特性，当管网规模较大时，不同污染源位置的个体间适应度值相差较大，基本的轮盘赌选择算子容易让算法陷入局部最优，因此，采用改进轮盘赌选择方法。改进轮盘赌选择方法具体如下：针对种群p，采用基本的轮盘赌选择得到新种群np；统计新种群np中污染源位置相同个体出现的次数；对相同污染源位置出现次数大于或等于n次的个体保留其中适应度最好的个体npi复制到种群pi中，n根据实验经验值得出，而余下的n-1个个体不进行复制，相应位置的种群p保留；若污染源位置出现次数小于n，直接将np中个体复制的到种群p中相应的位置。例如：种群p，如表1所示：表1种群pi12345678污染源位置2226282930481530经过基本轮盘赌选择得到np，如表2所示：表2新种群npi12345678污染源位置3022303028302622假设n＝4，统计污染源位置出现次数，污染源位置为30的出现了4次，假设i＝4位置的适应度最好，则更新后种群p如下表3所示：表3更新后种群pi12345678污染源位置2222263028482622s5.3.对子种群pl采用交叉算子和变异算子进行处理；对子种群pt采用交叉算子和邻近搜索策略进行处理；对子种群pm采用交叉算子和改进的变异策略进行处理；当开始时间和持续时间陷入局部最优时，普通的交叉变异算子很难跳出，比如说(2，4)是真实污染源事件的开始时间和持续时间，但是算法中陷入(3，3)局部时，很难达到(2，4)，因为通常陷入局部最优解时，说明大部分个体都是这个值，而此时交叉已经很难起到作用，而突变算子从(3，3)到(2，4)的概率非常的小。因此，提出了一种邻近搜索机制，在能够保持个体多样性下，又能很好的跳出局部最优，把开始时间和持续时间看做一个整体，每次迭代中，它们共同决定一个时间序列，去搜索和它重合程度最高的时间序列，模仿哈雷编码的原理，搜索后得到的时间序列与本身只是相差一个时间段，如表4所示。表4邻近搜索改进的变异策略为结合粒子群优化算法的思想，去向着最好的个体变异，且加入了一个自适应因子，来保证个体的多样性，改进的变异策略的算法在运行过程中，自适应因子会随着算法的收敛，逐渐变小，使得变异的范围能够自适应的调整。自适应因子的公式为：individual(ij)＝(individual(ij)+bestindividual(ij))/2+rand*maxdistance式中：individaul表示个体，i表示需要进行突变的序号，即表示维度，bestindividual表示的是pm种群中的最好的个体，rand表示(0，1)之间的随机数，maxdistance表示在第j维中所有个体的最大间距。s5.4.步骤s5.3中针对交叉算子和变异算子产生的新个体采用高斯预测模型预测个体适应度值μ和预测误差σ，如果触发系数3σ/μ＜0.2直接使用高斯预测模型预测个体适应度值μ作为新个体适应度值，否则，随机生成一个概率p*，如果p*＜p,p＝t/x使用网平差软件计算个体适应度值，其中，t表示迭代次数，x为基数，否则，使用高斯预测模型预测个体适应度值。s5.5.在每一次迭代结束后，种群根据个体适应度值进行排序，对高斯预测模型预测的个体适应度值的前n个个体使用网平差软件重新计算个体适应度值进行校正，n为种群的10％，n数值上等于精英保留个体的个数，种群的前部分好的个体是真实适应度值，保持正确的进化方向；s5.6.对经过步骤s5.5处理的子种群pl、pt、pm分别使用精英策略，在pl种群中精英个体出现相同的情况下，采用扰动策略，在pm中对于每一精英个体直接使用扰动策略；精英个体出现相同时，大管网中有很多节点，由于水力的结构、水需求等的不同，导致不同节点对应的不同污染事件产生的适应度值差别很大，通常一个较好的适应度值个体要比绝大部分模拟污染事件(个体)要好，很容易造成局部最优，尽可能的增加多样性，当精英个体出现相同时，进行扰动搜索附近的某个节点，改善定位问题，拓扑结构相近的节点对应的编号不相同，单靠演化算法的搜索机制，向着好的个体收敛，由于编号不连续所以并没有达到效果，因为实际上希望的是拓扑结构上向着好的个体收敛，故采用扰动正好能够搜索拓扑结构邻近个体，从而得到更好的个体。而当扰动后出现好的适应度值时，才替换，否则直接选用种群中不一样的仅次于(适应度值)相同精英个体的个体，其实也是为了保持多样性，pm也一样，精英个体也不一定被扰动。污染源定位问题中特别是大管网中，很容易定位到一个好的区域，但是也容易陷入局部最优，分析了整个管网拓扑结构后发现，它的位置并不是连续的，也就是说一个节点的周围其他节点在拓扑结构上是相近的，但是它们的位置标签却不是连续的。为了解决这一问题，在污染源位置的搜索中，加入扰动的策略。在精英策略中精英个体出现相同的情况下，则对相同个体进行扰动，这里的扰动结合污染源问题特性，是在位置上去搜索管网拓扑结构相近的节点，当出现有更好的个体(评估函数评价)时替换相同的精英个体，没有更好个体时，则直接选用种群中不一样的仅次于相同精英个体(即在适应度值上)的个体。s5.7.经过s代的整数倍，协同算法涉及到信息的交流，s值太大会导致种群之间交流太少，种群得不到其他种群变量信息更新，容易陷入局部最优，值太小会导致种群失去自身独立搜索的次数，信息更新时的部分变量并不是优秀的，优选是5代，子种群pl、pt、pm把最优个体的对应基因相互组合产生新的个体，并均匀加入的子种群pl、pt、pm直接替换对应的最差个体；s5.8.达到最大迭代次数，则结束。本实验采用bwsn管网。管网总模拟时间为48小时，模拟的水力时间步长为1小时，水质时间步长为5分钟，真实污染场景是模拟开始2小时后从节点4529持续注入2小时污染物。实验平台：处理器为intelcorei5-6500@3.20ghz，内存为8.0gb，操作系统为windows7专业版64位操作系统。本文实验是算法性能分析，然后对比算法使用代理模型和不使用代理模型的差异，通过对epanet评价次数和算法的时间成本进行分析，验证基于高斯预测模型的昂贵优化算法的有效性和高效性。算法性能分析：在算法收敛过程中，大量使用高斯预测模型可以大大减少时间成本的消耗，如图5所示，显示了使用一次高斯预测模型预测和使用一次epanet模拟器计算个体适应度值所需的时间对比，一次高斯预测模型比epanet模拟器减少时间约，可以证明大量使用高斯预测模型能大大的减少算法时间成本的开销。如表5所示，显示以上提出的四种算法运行结果，虽然不使用代理模型的最优解适应度值更低，但是不影响污染源定位位置的精度，定位结果只在污染物注入质量上有一点偏差，四个算法都定位到真实污染源位置4529，且污染物注入质量向量也相似。表5实验结果在同时都能准确定位的情况下，使用高斯预测模型与不使用高斯预测模型的算法的epanet使用次数与消耗时间如图6所示，在相同结果情况下，使用高斯预测模型的算法epanet使用次数大幅度减少，将近减少2/3倍，从而使算法所消耗时间也大大减少，大大提升了算法的效率，验证了本文算法的有效性和高效性。如图7所示，经过多次的实验表明，本算法无论在定位污染源位置还是开始时间和持续时间上，都要明显优于加入高斯预测模型的普通ga。结合到上表2，相比于不加昂贵模型的算法，本文提出的算法大大减少了计算的时间，而相比于加入高斯预测模型的ga，虽然时间上平均提高了6分钟，但是算法的稳定性得到了很大的提升。本发明采用了协同算法，根据不同的种群，有针对性的采用不同的策略，有效的改善算法的稳定性。在本文中，所涉及的前、后、上、下等方位词是以附图中零部件位于图中以及零部件相互之间的位置来定义的，只是为了表达技术方案的清楚及方便。应当理解，所述方位词的使用不应限制本申请请求保护的范围。在不冲突的情况下，本文中上述实施例及实施例中的特征可以相互结合。以上所述仅为本发明的较佳实施例，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页12