一种间隔均布载荷椭圆横截面等强度支承梁的制作方法

本实用新型涉及一种间隔均布载荷椭圆横截面等强度支承梁，属机械结构设计与制造技术领域。

背景技术：

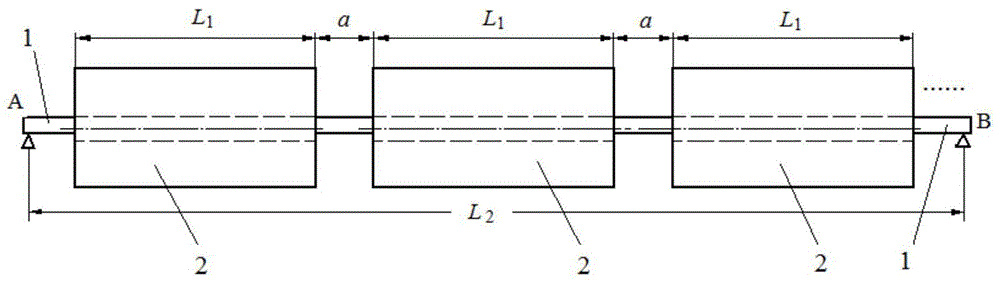
在生产实际中经常会遇到承受间隔均布载荷的大梁的技术问题，例如，铝箔生产厂的铝箔在热处理等工序中需要用大梁支承着。铝箔是成卷生产的，铝箔缠卷在一个中空的的芯子外面，一个铝卷约300kg至2000kg，在热处理炉中，由一条大梁穿过芯子支承若干个铝箔卷，各铝箔卷之间有一定间隔。如图1是铝箔卷支承示意图，长为l2的大梁穿过芯子支承着若干个铝箔卷，等效于承受着间隔均布载荷，各铝箔卷之间的间隔为a，可用图2来表示这类工程问题的力学模型。力学模型图2适合于任何类似的承受间隔均布载荷梁的工程技术问题。图2中，l1为均布载荷所分布的长度、q为均布载荷的集度或称线密度(单位为n/m或kn/m)、x为梁ab的任一截面到梁ab左端a的距离、v为支座反力。

由于外载荷很大，外载荷的作用方式也较特殊，支承梁的强度与刚度问题便成为亟待解决的工程技术问题。传统的设计大都是以限定梁的最危险截面的最大应力来确定梁的结构尺寸的，整个梁的尺寸跟最危险截面处的尺寸一样大小，这样，应力小的地方，材料没有充分发挥作用，不但造成浪费，而且增加了梁的重量，使成本增加且操作使用困难。更为科学合理的理念应该是，在保证安全可靠的前提下，以最经济的代价，为构件确定合理的形状和尺寸。对于本实用新型所涉及的承受间隔均布载荷的椭圆形横截面等强度支承梁，如果能构造一种特殊结构尺寸的梁，使梁各个横截面处于同等强度下，各个横截面的最大应力处处相等，便可达到既安全可靠又科学、经济的技术效果。根据相关专业知识，这是可以实现的，以下将作出具体分析。在数控加工技术日益发达的时代，这样的结构也是容易加工制造的。

技术实现要素：

本实用新型解决其技术问题所采用的技术方案是：构造一种间隔均布载荷椭圆横截面等强度支承梁，其特征是：这种梁承受间隔均布载荷，即每隔一定的等距离承受着沿梁长度方向每单位长度均匀分布的载荷，这种梁的横截面为实心椭圆或空心椭圆(椭圆环)，这种梁的椭圆横截面的一条半轴，即横向半轴为b，另一条半轴即纵向半轴c随梁的长度方向尺寸x而变化，即在距离梁左端x处的横截面的椭圆的半轴为c(x)，梁的高度为2c(x)；(1)当梁的横截面为实心椭圆时，梁的椭圆横截面在梁的间隔段(无外载荷段)的纵向半轴为其中k为梁间隔段(无外载荷段)的段数标号且k为奇数、a为梁间隔段(无外载荷段)的长度、l1为每段均布载荷所分布的长度、q为梁所承受的总载荷(即梁上各段均布载荷的合力)、n为梁所承受的均布载荷的段数、[σ]为梁材料的拉压许用应力；梁在承受均布载荷区段的椭圆截面的纵向半轴为其中k为梁承受均布载荷区段的段数标号且k为偶数、其余符号意义同前；(2)当梁的横截面为空心椭圆时，椭圆纵向半轴c(x)符合以下结构尺寸的约束条件：其中t为空心椭圆周边的宽度、[σ]为梁材料的拉压许用应力、mk(x)为梁在x截面处的弯矩，mk(x)分以下两种情况：(i)当mk(x)为梁在其间隔段(无外载荷段)所承受的弯矩且段数标号k为奇数时，其中a为梁间隔段(无外载荷段)的长度、l1为每段均布载荷所分布的长度、q为梁所承受的总载荷、n为梁所承受的均布载荷的段数；(ii)当mk(x)为梁在均布载荷的分布区段所承受的弯矩且段数标号k为偶数时，其余符号意义同前。这种梁所承受的间隔均布载荷集度或线密度为各符号含义同前。当梁的横截面为实心椭圆横截面时，梁的最小纵向半轴是且cmin≥t、t≤b；当梁的横截面为空心椭圆横截面时，梁的最小纵向半轴是且cmin≥t、t≤b；其中[τ]为梁材料的剪切许用应力，其余符号含义同前。

本实用新型的有益效果是：梁的强度处处相等，节约材料，精简结构，降低重量。

附图说明

图1铝箔卷支承示意图。

图2受间隔均布载荷梁的力学模型图。

图3实施例二工况下的等强度支承梁。

图4实施例三工况下的等强度支承梁。

图1中：1是支承梁、2是铝箔卷。

图2中：l1为均布载荷所分布的长度、q为均布载荷的集度或称线密度(单位为n/m或kn/m)、l2为梁的总长度、x为梁ab的任一截面到梁ab左端a的距离、v为支座反力、q为梁所承受的总载荷(即梁上各段均布载荷的合力)、a为各铝箔卷之间的间隔。

具体实施方式

要做到等强度，首先要对梁的外载荷特点、内力(矩)特点与规律、各参数的变化趋势与规律进行分析研究，根据研究结果，采取相应的技术措施。由于本实用新型所涉及的梁其外载荷特殊，因此本实用新型的技术方案与技术措施也必然会很特殊。

如图2，ab代表受间隔均布载荷的椭圆形横截面支承梁。梁全长为l2，其上共作用n段均布载荷，n段均布载荷的合力，即梁所承受的总载荷是qn，每段均布载荷的集度，即线密度是qn/m，每段均布载荷的分布长度是l1，每段均布载荷之间的间隔是a；根据有关专业知识，可以得到距离梁左端为x处(参阅图2)的横截面上的内力矩如下：

(i)间隔段(无外载荷段)的弯矩

当mk(x)为梁间隔段(无外载荷段)所承受的弯矩且段数标号k为奇数时，

其中k为段数标号，且k为奇数、其余各符号意义同前。

(ii)梁在承受均布载荷区段的弯矩

当mk(x)为梁在承受均布载荷区段所承受的弯矩且段数标号k为偶数时，

其中k为段数标号，且k为偶数、其余各符号意义同前。

经过分析研究，可以得出以下特点：

(1)间隔均布载荷梁内弯矩具有对称性，即m1(x)＝m2n+1(l2-x)、m2(x)＝m2n(l2-x)、m3(x)＝m2n-1(l2-x)、m4(x)＝m2n-2(l2-x)...mk(x)＝m2n-k+2(l2-x)。

(2)承受偶数段均布载荷时(k为奇数)，最大弯矩在全梁中间那个间隔段的中点处，且为常数此时k为奇数，k＝n+1。

(3)承受奇数段均布载荷时(k为偶数)，最大弯矩在全梁中间那个铝卷的中点处，为若则此时k为偶数，k＝n+1；所述为全梁在完全均布载荷作用下的最大弯矩。

(4)综上，n段均布载荷时，间隔段有n+1段，共2n+1段，弯矩个数为2n+1；n为奇数时，最大弯矩是偶数号弯矩mk＝mn+1(即k＝n+1)，发生在正中间的均布载荷段的正中点，即第n+1段的中点，也即处，即全梁的中点，最大弯矩是

顺便指出，若l1＝l2，这意味着a＝0，n＝1，此时上式成为这是众所周知的全梁受完全均布载荷(无间隔)时的最大弯矩。n为偶数时，最大弯矩是奇数号弯矩mk＝mn+1(即k＝n+1)，发生在第n+1个间隔段，且在整个第n+1段上为常数，也即从到上为常数，最大弯矩是

此外，对于奇数段(间隔段)弯矩

这是直线方程，显然，k<n+1时，mk随x增大而上升；k>n+1时，mk随x增大而下降；k＝n+1时，mk为常数，与x无关，为与前述完全吻合。

对于偶数序号，即均布载荷段弯矩

这是抛物线方程，令得

要使x0落在之内，须有

n<k<n+2，由于n、k均为正整数，故有k＝n+1，当k＝n+1时，即在整个梁的中点。最大值是若不满足k＝n+1的关系，mk的最大值不在内。又由于k为偶数，故n为奇数。也与前述完全吻合。

对于纵向半轴，亦即梁高也有类同结论，即：

对于奇数段(间隔段，即无外载荷段)的纵向半轴

k<n+1时，ck(x)随x增大而上升；k>n+1时，ck(x)随x增大而下降；k＝n+1时，ck(x)为常数，与x无关，为

对于偶数序号，即均布载荷段的纵向半轴

令得

这与mk(x)的驻点完全一致，要使x0落在之内，须有n<k<n+2，由于n、k均为正整数，故有k＝n+1，当k＝n+1时，即在整个梁的中点。若不满足k＝n+1的关系，ck的最大值不在内。又由于k为偶数，故n为奇数。当时，ck的最大值是

显然，若梁的尺寸由全梁的最大弯矩决定，梁势必很庞大(参见以下实施例)，这既不经济也不安全，因为结构太笨重不但浪费人力、物力、财力，操作使用也很不方便。本实用新型的技术思想就是使梁的结构尺寸适应于上述内力矩的特殊变化，以达到梁处处等强度的技术效果。

实施例一，设实心椭圆截面梁上的均布载荷的段数n＝5，则奇数号弯矩最大序号为m2n+1，即m11，偶数号弯矩最大序号为m2n，即m10；5段均布载荷总载荷q＝73.5kn，故支座反力v＝q/2＝36.75kn；梁长l2＝3m，各段均布载荷之间间隔从而l1＝564mm，均布载荷根据式(1)(奇数段，即间隔段的弯矩)和式(2)(偶数段，即均布载荷段的弯矩)以及本实用新型的技术方案，可得各区段的弯矩mk(x)(knm)和梁的高度尺寸hk(x)(m)如下：

第1段0≤x≤a，即0≤x≤0.03m段，k＝1：

可以验证，即在整个第一段，每个横截面上的最大应力都恒为常数[σ]，其中w1为第一段椭圆形横截面的抗弯截面系数，

第2段a≤x≤a+l1，即0.03m≤x≤0.594m段，k＝2：

可以验证，即在整个第二段，每个横截面上的最大应力都恒为常数[σ]，其中w2为第二段椭圆形横截面的抗弯截面系数，

用s表示起点，用u表示终点，可以验证，x＝a时，m1u＝m2s。

第3段a+l1≤x≤2a+l1，即0.594m≤x≤0.624m段，k＝3：

可以验证，x＝2a+l1时，m2u＝m3s。

可以验证，即在整个第三段，每个横截面上的最大应力都恒为常数[σ]，其中w3为第三段椭圆形横截面的抗弯截面系数，

同理可验证，以下各段均有即各段的每个横截面上的最大应力都恒为常数[σ]，其中为第k段椭圆形横截面的抗弯截面系数。这就是等强度的优势。

第4段2a+l1≤x≤2a+2l1，即0.624m≤x≤1.188m段，k＝4：

x＝2a+l1时，m3u＝m4s；且，m4max＝m4u。

第5段2a+2l1≤x≤3a+2l1即1.188m≤x≤1.218m段，k＝5：

可以验证，x＝2a+2l1时，m4u＝m5s。

第6段3a+2l1≤x≤3a+3l1即1.218m≤x≤1.782m段，k＝6：

可以验证，x＝3a+3l1时，m5u＝m6s＝m5max。

令得

正好是3a+2l1与3a+3l1中点(当n＝5时)。最大的弯矩是m6，在处，为

mmax＝m6max＝q(0.9a+0.625l1)＝27.89325knm。

第7段3a+3l1≤x≤4a+3l1即1.782m≤x≤1.812m段，k＝7：

第9段4a+4l1≤x≤5a+4l1即2.376m≤x≤2.406m段，k＝9：

第11段5a+5l1≤x≤6a+5l1即2.97m≤x≤3m段，k＝11：

第8段4a+3l1≤x≤4a+4l1即1.812m≤x≤2.376m段，k＝8：

第10段5a+4l1≤x≤5a+5l1即2.406m≤x≤2.97m段，k＝10：

若以全梁最大弯矩mmax＝m6max＝27.89325knm控制梁高，则全梁高度为常数若取[σ]＝170000kn/m²、b＝40mm，则整个梁每一横截面的高度都必须为2c＝144.537375mm，这正是等强度梁最高处的纵向半轴：

取剪切许用应力[τ]＝90mpa时，最小纵向半轴根据本实用新型的技术方案，梁的首末两端，即0～10mm段和2990～3000mm段的纵向半轴为8mm。

本实用新型所述等强度梁的梁高2ck(x)即具备上述特征和规律，形状、尺寸符合上述特征和规律的梁，其强度必定处处相同，即各个横截面的最大应力都相等。实施例二和实施例三亦如是，并且实施例二和实施例三也给出了等强度的验证。

实施例二，设实心椭圆形截面梁上的均布载荷的段数n＝5，则奇数号弯矩最大序号为m2n+1，即m11，偶数号弯矩最大序号为m2n，即m10；5段均布载荷总载荷q＝73.5kn，故支座反力v＝q/2＝36.75kn；梁长l2＝3m，各段均布载荷之间间隔从而l1＝360mm，均布载荷根据式(1)(奇数段，即间隔段的弯矩)和式(2)(偶数段，即均布载荷段的弯矩)以及本实用新型的技术方案，可得各区段的弯矩mk(x)(knm)和梁的纵向半轴ck(x)(m)如下(2ck(x)即为梁高)。

(实施例一、二的外载荷完全相同，弯矩、纵向半轴ck(x)的表达式形式也完全一样，但均布载荷的间隔不同，因而弯矩所适合的区段长度不同，由此也导致弯矩、纵向半轴的大小不同，从而二者的梁高有不同)

第1段0≤x≤a，即0≤x≤0.2m段，k＝1：

可以验证，即在整个第一段，每个横截面上的最大应力都恒为常数[σ]，其中w1为第一段椭圆形横截面的抗弯截面系数，

第2段a≤x≤a+l1，即0.2m≤x≤0.56m段，k＝2：

可以验证，即在整个第二段，每个横截面上的最大应力都恒为常数[σ]，其中w2为第二段椭圆形横截面的抗弯截面系数，

用s表示起点，用u表示终点，可以验证，x＝a时，m1u＝m2s。

第3段a+l1≤x≤2a+l1，即0.56m≤x≤0.76m段，k＝3：

可以验证，x＝2a+l1时，m2u＝m3s。

可以验证，即在整个第三段，每个横截面上的最大应力都恒为常数[σ]，其中w3为第三段椭圆形横截面的抗弯截面系数，

同理可验证，以下各段均有即各段的每个横截面上的最大应力都恒为常数[σ]，其中为第k段椭圆形横截面的抗弯截面系数。这就是等强度的优势。

第4段2a+l1≤x≤2a+2l1，即0.76m≤x≤1.12m段，k＝4：

x＝2a+l1时，m3u＝m4s；且，m4max＝m4u。

第5段2a+2l1≤x≤3a+2l1即1.12m≤x≤1.32m段，k＝5：

可以验证，x＝2a+2l1时，m4u＝m5s。

第6段3a+2l1≤x≤3a+3l1即1.32m≤x≤1.68m段，k＝6：

可以验证，x＝3a+3l1时，m5u＝m6s＝m5max。

令得

正好是3a+2l1与3a+3l1中点(当n＝5时)。最大的弯矩是m6，在处，为

mmax＝m6max＝q(0.9a+0.625l1)＝29.7675knm

第7段3a+3l1≤x≤4a+3l1即1.68m≤x≤1.88m段，k＝7：

第9段4a+4l1≤x≤5a+4l1即2.24m≤x≤2.44m段，k＝9：

第11段5a+5l1≤x≤6a+5l1即2.8m≤x≤3m段，k＝11：

第8段4a+3l1≤x≤4a+4l1即1.88m≤x≤2.24m段，k＝8：

第10段5a+4l1≤x≤5a+5l1即2.44m≤x≤2.8m段，k＝10：

若以全梁最大弯矩mmax＝m6max＝29.7675knm控制梁高(等于纵向半轴的2倍)，则全梁高度为常数若取[σ]＝170000kn/m²、b＝40mm，则整个梁每一横截面的高度都必须为2c＝149.314431mm，这正是等强度梁最高处的高度：

取剪切许用应力[τ]＝90mpa时，最小纵向半轴根据本实用新型的技术方案，梁的首末两端，即0～10mm段和2990～3000mm段的纵向半轴为8mm。

梁的形状、尺寸由上述表达式和数据确定，就本实施例所给的工况条件，具备上述特征的梁一定是等强度梁。图3即是实施例二的等强度梁的示意图。

实施例三，各工况参数同实施例二，采用空心椭圆截面梁，均布载荷的段数n＝5，奇数号弯矩最大序号为m2n+1，即m11，偶数号弯矩最大序号为m2n，即m10；5段均布载荷总载荷q＝73.5kn，故支座反力v＝q/2＝36.75kn；梁长l2＝3m，各段均布载荷之间间隔从而l1＝360mm，均布载荷根据式(1)(奇数段，即间隔段的弯矩)和式(2)(偶数段，即均布载荷段的弯矩)以及本实用新型的技术方案与措施，可得各区段的弯矩mk(x)(knm)如实施例二所述。空心椭圆形截面高度c(x)符合以下结构尺寸的约束条件：

其中t为空心椭圆周边宽度、[σ]为梁材料的拉压许用应力(同实施例二)、mk(x)为梁在x截面处的弯矩，与实施例二完全一样。为展示具体实施过程，现对上述约束条件作进一步说明。将上式变形成

令a＝t，b＝3t(b－t)，

又令

则有：

(1)若δ>0，

(2)若δ＝0且p≥0，或

(3)若δ<0，

或

或

其中

梁的纵向半轴ck(x)具备上述规律和特征的，必然是等强度梁，即梁的强度处处相等，亦即梁每个横截面上的最大应力均相等。可根据上述规律选择合理、最优的梁高，且保证最小纵向半轴且cmin≥t、t≤b。以本实施例的工况条件为例，取椭圆的横向半轴b＝40mm，t＝10mm，拉压许用[σ]＝170mpa，剪切许用应力[τ]＝90mpa。最小纵向半轴这意味着任何梁高都能满足强度要求。根据本实用新型的技术方案，在梁的首末两端，即在0～10mm段和2990～3000mm段取2c＝20mm＝2t>－8.0095mm，见表1和表4括号中的数据。

根据本实用新型的技术方案，等强度梁各处的弯矩及梁高如下(实施例二、三的弯矩及其所适合的区段长度完全相同，但横截面不同，从而二者的梁高有不同)。为了显示尺寸数值，以下对于纵向半轴不是如实施例二那样给出表达式，而是沿梁长每隔10mm列出了具体数据，见表1～表4。为验证本实用新型的技术效果，以下随机抽取了几组数据进行查验。

第1段0≤x≤a，即0≤x≤0.2m段，k＝1：m1(x)＝vx＝qx/2＝36.75x；

第3段a+l1≤x≤2a+l1，即0.56m≤x≤0.76m段，k＝3：

第5段2a+2l1≤x≤3a+2l1即1.12m≤x≤1.32m段，k＝5：

梁的第1、3、5段弯矩与梁高数值见表1。

验证：

(1)第1段取x＝100mm处的数据(见表1)：梁纵半轴c(x＝100)＝59.350/2mm(精确数据是59.34991139/2＝29.674956mm)，弯矩m(x)＝3.675knm，前述已定b＝40mm，t＝10mm。于是

代入t＝0.01m，c(x)＝0.029674956m，b＝0.04m得w＝2.16176×10^-5m³。

最大应力为

(2)再取第8段x＝2000mm处的数据(见表4)：梁纵半轴c(x＝2000)＝211.425/2mm(精确数据是c(x＝2000)＝105.7123767mm)，弯矩m(x)＝26.46knm，代入t＝0.01m，c(x＝2000)＝0.1057123767m，b＝0.04m得w＝0.000155647m³。

最大应力为其他各处的应力可做同样计算，其结果处处都有最大应力σ＝170mpa。这就是本实用新型所达到的等强度优势。

第7段3a+3l1≤x≤4a+3l1即1.68m≤x≤1.88m段，k＝7：

第9段4a+4l1≤x≤5a+4l1即2.24m≤x≤2.44m段，k＝9：

第11段5a+5l1≤x≤6a+5l1即2.8m≤x≤3m段，k＝11：

梁的第7、9、11段弯矩与梁高数值见表2。

第2段a≤x≤a+l1，即0.2m≤x≤0.56m段，k＝2：

第4段2a+l1≤x≤2a+2l1，即0.76m≤x≤1.12m段，k＝4：

第6段3a+2l1≤x≤3a+3l1即1.32m≤x≤1.68m段，k＝6：

梁的第2、4、6段弯矩与梁高数值见表3。

第8段4a+3l1≤x≤4a+4l1即1.88m≤x≤2.24m段，k＝8：

第10段5a+4l1≤x≤5a+5l1即2.44m≤x≤2.8m段，k＝10：

梁的第8、10段弯矩与梁高数值见表4。

有了如表1～4的数据就确定了等强度梁的具体尺寸与形状。由实施例三的工况条件和本实用新型的技术方案所得到的等强度梁如图4所示。与实施例二比较，实施例三的梁高大于实施例二的梁高，但由于实施例三的梁是空心的，其横截面积更小，利用表1～表4的梁高数据可验证这一点。

表1第1、3、5段弯矩与梁高数值

表2第7、9、11段弯矩与梁高数值

表3第2、4、6段弯矩与梁高数值

表4第8、10段弯矩与梁高数值