双Buck全桥逆变器迭代学习控制方法与流程

本发明属于逆变器建模与控制技术领域，具体地说，涉及一种双buck全桥逆变器迭代学习控制方法。

背景技术：

逆变技术通过功率开关器件将直流电能变换为交流电能，其在新能源发电、不间断电源、调速系统等领域具有至关重要的地位。然而传统桥式逆变器由于开关管的体二极管性能差，导致很大损耗并限制了开关频率的提高。而双buck逆变电路功率开关管和功率二极管可以分别得到最优设计，该变换器同时克服了传统桥式逆变器的直通问题，且电压利用率高。

然而，由于输入直流电源波动、死区效应、稳态时线性和非线性负载电流的扰动会引起逆变器周期性扰动，使输出波形发散畸变。会对逆变器上的其他设备造成影响、无法正常工作，严重时会导致其损坏。因此在主电路拓扑固定的情况下，提出一种合适的控制策略解决周期性扰动问题十分必要。

技术实现要素：

本发明的目的在于提供一种双buck全桥逆变器迭代学习控制方法，该方法可确保双buck全桥逆变器有较好的负载适应能力和优越的跟踪性能。

为实现上述目的，本发明的技术方案是：一种双buck全桥逆变器迭代学习控制方法，针对逆变器在直流电源波动、死区效应、稳态时线性和非线性负载电流扰动产生的周期性扰动，采用电压外环迭代学习控制+电流内环无差拍控制的双环控制策略，提高双buck逆变器的输出效率，使系统输出电压能精确跟踪参考信号，并增强系统稳定性和提高动态响应性能。

在本发明一实施例中，该方法具体实现步骤如下，

根据基尔霍夫电压和电流定律，由于滤波电感l1、l2的电流il1(t)＝il2(t)，可令il1(t)＝il2(t)＝il(t)，且令电感量l1＝l2＝l，由于逆变器正负半周对称，因此此处仅分析正半周，可令ua(t)＝u(t)，得逆变器系统模型如下：

其中，c为滤波电容的电容值；

选择电容电压uc和电感电流il为状态变量，逆变器交流输出电压u(t)和负载电流ir(t)为输入，电容电压uc为系统输出；于是，x(t)＝[uc(t),il(t)]，u(t)＝[u(t),ir(t)]，y(t)＝uc(t)；逆变器系统状态方程为：

其中，c＝(10)

由于直流电源波动、死区效应、稳态时线性和非线性负载电流扰动引起的周期性扰动，对应的逆变器系统状态方程可写为：

其中，w(t)，v(t)为周期性扰动；为解决该周期性扰动，采用电压外环迭代学习控制+电流内环无差拍控制的双环控制策略，具体策略如下：

设负载参考电压为yd(t)，负载采样电压为yk(t)，可得输出误差为：ek(t)＝yd(t)-yk(t)，采用迭代学习控制开闭环p型学习律进行迭代，对应学习律公式如下：

uk+1(t)＝uk(t)+γ1(t)ek(t)+γ2(t)ek+1(t)

得迭代学习控制算法流程如下：

(1)初始时，设负载参考电压为yd(t)，初始控制量为u0(t)，时间间隔为t∈[0,t]；

(2)系统的初始输出量为yk(0)，初始状态量为xk(0)；

(3)使控制输入量uk(t)输入到被控系统中，得系统输出量为yk(t)，重复操作；

(4)在时间间隔t∈[0,t]内负载采样电压与参考电压的误差为ek(t)＝yd(t)-yk(t)；采用上式学习律公式计算，得新的控制输入量为uk+1(t)；

(5)判断，迭代是否满足了停止条件(预设的迭代次数)，如果满足就停止；否则，令k＝k+1，转到步骤(2)，继续运行；

经若干次迭代后，使得yk(t)→yd(t)；

迭代学习控制开闭环p型学习律若满足||i-γ1(t)d(t)||·||[i+γ2(t)d(t)]-¹||＜1，则控制律收敛；由此可计算出γ1(t)、γ2(t)的值；

由于迭代学习控制动态性能较差，对此采样两电感电流作为内环控制，由于电流比电压有更快的响应速度，系统的许多变化都会第一时间在电流上有所表现，所以内环电流控制能起到增强系统稳定性和提高动态响应性能的能力。

相较于现有技术，本发明具有以下有益效果：本发明采用新型器件sicmosfet，提出了电压外环迭代学习控制+电流内环无差拍控制的双环控制策略不仅保留了双buck全桥逆变器无桥臂直通问题，提高双buck逆变器的输出效率，电压利用率高，且解决了直流电源波动、死区效应、稳态时线性和非线性负载电流扰动引起的周期性扰动问题。

附图说明

图1为双buck全桥逆变器主电路拓扑图。

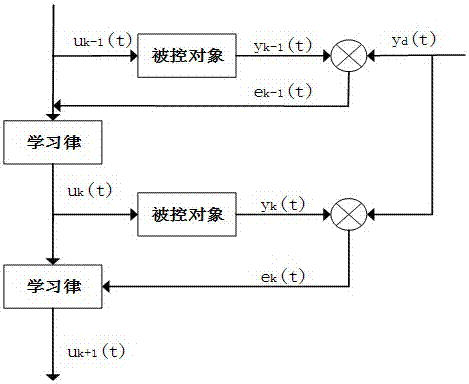
图2为迭代学习控制算法流程图。

图3为传统双环pid控制输出电压仿真波形图。

图4为迭代学习控制下输出电压仿真波形图。

图5为迭代学习控制下参考和实际输出电压仿真波形图。

图6为加周期性扰动后传统双环pid控制输出电压仿真波形图。

图7为迭代学习控制下加周期性扰动后参考与实际输出电压波形图。

具体实施方式

下面结合附图1-7，对本发明的技术方案进行具体说明。

本发明的一种双buck全桥逆变器迭代学习控制方法，针对逆变器在直流电源波动、死区效应、稳态时线性和非线性负载电流扰动产生的周期性扰动，采用电压外环迭代学习控制+电流内环无差拍控制的双环控制策略，使系统输出电压能精确跟踪参考信号，提高双buck逆变器的输出效率，并增强系统稳定性和提高动态响应性能；该方法具体实现步骤如下，

根据基尔霍夫电压和电流定律，由于滤波电感l1与l2的电流il1(t)＝il2(t)，可令il1(t)＝il2(t)＝il(t)，且令电感量l1＝l2＝l，滤波电容c，由于逆变器正负半周对称，因此这里只分析正半周，可令ua(t)＝u(t)，得逆变器系统模型如下：

选择电容电压uc和电感电流il为状态变量，逆变器交流输出电压u(t)和负载电流ir(t)为输入，电容电压uc为系统输出；于是，x(t)＝[uc(t),il(t)]，u(t)＝[u(t),ir(t)]，y(t)＝uc(t)；逆变器系统状态方程为：

其中，c＝(10)

由于直流电源波动、死区效应、稳态时线性和非线性负载电流扰动引起的周期性扰动，对应的逆变器系统状态方程可写为：

其中，w(t)，v(t)为周期性扰动；为解决该周期性扰动，采用电压外环迭代学习控制+电流内环无差拍控制的双环控制策略，具体策略如下：

设负载参考电压为yd(t)，负载采样电压为yk(t)，可得输出误差为：ek(t)＝yd(t)-yk(t)，采用迭代学习控制开闭环p型学习律进行迭代，对应学习律公式如下：

uk+1(t)＝uk(t)+γ1(t)ek(t)+γ2(t)ek+1(t)

得迭代学习控制算法流程如下：

(1)初始时，设负载参考电压为yd(t)，初始控制量为u0(t)，时间间隔为(t∈[0,t])。

(2)系统的初始输出量为yk(0)，初始状态量为xk(0)。

(3)使控制输入量uk(t)(t∈[0,t])输入到被控系统中，得系统输出量为yk(t)(t∈[0,t])。重复操作。

(4)在一定时间间隔(t∈[0,t])内负载采样电压与参考电压的误差为ek(t)＝yd(t)-yk(t)。采用上式迭代学习律计算，得新的控制输入量为(t∈[0,t])uk+1(t)。

(5)判断，迭代是否满足了停止条件(预设的迭代次数)，如果满足就停止。否则，令k＝k+1，转到步骤(2)，继续运行。

经若干次迭代后，使得yk(t)→yd(t)；

该迭代学习控制开闭环p型学习律若满足||i-γ1(t)d(t)||·||[i+γ2(t)d(t)]^-1||＜1，则控制律收敛；由此可计算出γ1(t)、γ2(t)的值；

然而，迭代学习控制动态性能较差，对此采样两电感电流作为内环控制，由于电流比电压有更快的响应速度，系统的许多变化都会第一时间在电流上有所表现，所以内环电流控制能起到增强系统稳定性和提高动态响应性能的能力。

以下为本发明的具体实施过程。

本发明方法的主电路拓扑如图1所示。

本发明主要研究双buck全桥逆变器，用电压迭代学习控制+电流无差拍控制的控制策略来解决周期性扰动问题。具体实例如下：

仿真验证

为了验证本发明方法的可行性，在psim下进行仿真实验。仿真结果验证了所设计控制策略的效果。

仿真参数选取如下：

表1：系统整体相关参数

图3为传统双环pid控制输出电压仿真波形图，由图可以看出系统能很好跟踪参考波形。

图4为迭代学习控制下输出电压仿真波形图，由图可以看出thd值只有2.03％。

图5为迭代学习控制下参考和实际输出电压仿真波形图，由图可以看出在0.17s处系统完全跟踪。

图6为加周期性扰动后传统双环pid控制输出电压仿真波形图，由图当加入扰动时，传统双环控制策略下的输出波形发生波动，thd达6.03％；图7是迭代学习控制下加周期性扰动后参考与实际输出电压波形图，由图可以看出迭代学习控制策略下输出电压波形能迅速消除扰动影响且短时间内达到完全跟踪，thd为1.32％。

由上述说明了本发明具有较好的负载适应能力和优越的跟踪性能。

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。