一种智能电网中基于博弈论的中继选择和功率分配方法与流程

本发明涉及无线通信技术领域，具体涉及一种智能电网中基于博弈论的中继选择和功率分配方法。

背景技术：

未来的无线通信网络通过中继传输可以实现全范围信号的覆盖，减少通信盲区的影响，改善通信传输质量。通过中继的协作传输，可以有效利用无线网络的广播特性，实现空间分集。协作中继网络中的中继选择和在不同中继节点上的功率分配可以极大地影响网络的性能。

未来的协作中继网络中，中继节点可能为不同的服务商或个人所提供，具有自私特性，同时对资源的需求具有非均质约束特性，这些使得通过有效激励机制实现节点的协作传输成为必然。另一方面智能电网作为下一代电能网络与现状传统的电网有着很大的差异，这对无线网络通信技术领域产生的影响也将会有所不同。在未来的智能电网中，可再生能源在电网中起到非常关键的作用，由于不同可再生能源的产生条件不同因此电网在进行能量传输时所提供的价格也有所不同，因此在通信网络中进行中继选择和功率分配时要考虑的因素。目前研究中的中继选择和功率分配时大部分仅考虑最优的功率选择以及中继选择，忽略了电网提供能量价格差异对最终决策所带来的影响。

技术实现要素：

为了克服现有技术存在的缺点与不足，本发明提供一种智能电网中基于博弈论的中继选择和功率分配方法。

本发明采用如下技术方案：

一种智能电网中基于博弈论的中继选择和功率分配方法，适用于半双工中继网络系统，包括一个源节点s、一个目的节点d以及k个中继节点，包括如下步骤：

s1用户在每个数据块传输之前，用户可选择中继协作模式，具体为：用户根据自身效用函数从k个中继节点中选择最合适的中继来建立协作通信链路。每个中继节点的报价为ηk(t)，所有中继构成报价集合为ψ(t)＝{η1(t),η2(t),…ηk(t)}；

s2用户对每个中继节点k的效用函数为us,k(ηk(t))，在得知每个中继报价集合ψ(t)的条件下，用户对每个中继节点选择最优购买功率pk来使得自身的效用函数达到最大值为用户对k个中继节点组成的效用函数最大值集合用户再从集合θ(ψ(t))选取最大值，其对应的中继节点为最优中继节点k^*＝argmax(θ(ψ(t)))；

s3最优中继k^*的利润函数若被选中继k^*能通过降价出售更多功率来获得更多利润，则更新报价集合ψ(t)＝{η1(t),η2(t),…ηk(t)}，若不降价则报价集合ψ(t)不变；

其他没有被用户选择的中继将进行通过降价来吸引用户，即η(t+1)＝max(η^min,η(t)-△η)，然后得到新的报价集合为ψ(t+1)＝{η1(t+1),η2(t+1),…ηk(t+1)}，如果ψ(t)＝ψ(t+1)则说明中继不再修改报价，用户和中继的策略不再发生变化即达到纳什均衡点，否则返回到s1中。

所述s1中中继的传输方式采用时分复用方式，在第一个时隙用户向基站发送数据，同时各个中继节点收到广播的数据块，第二个时隙内进行中继选择和功率分配，选中的中继k^*以功率pk向基站发送数据。

所述s2中用户自身对中继节点的效用函数其中为用户可达的中断容量。

所述s3中中继节点自身的利润函数为：uk(pk,ηk)＝(ηk-ck)pk，其中ck为中继的成本价格，即中继从智能电网中购入的价格。

所述s3中η^min为中继节点的所能降到的最低价格，即

本发明的有益效果：

本发明在中继选择和功率分配方法下引入经济学博弈论的方法，将用户建模为买者以最大效用为准则选择最优中继和最佳购买功率，将中继建模为卖者由智能电网提供不同的成本价格确定出售价格策略获得最大利润，本发明能够兼顾用户和中继节点的利益的同时有效提高传输速率，计算量较少而且收敛速度快。

附图说明

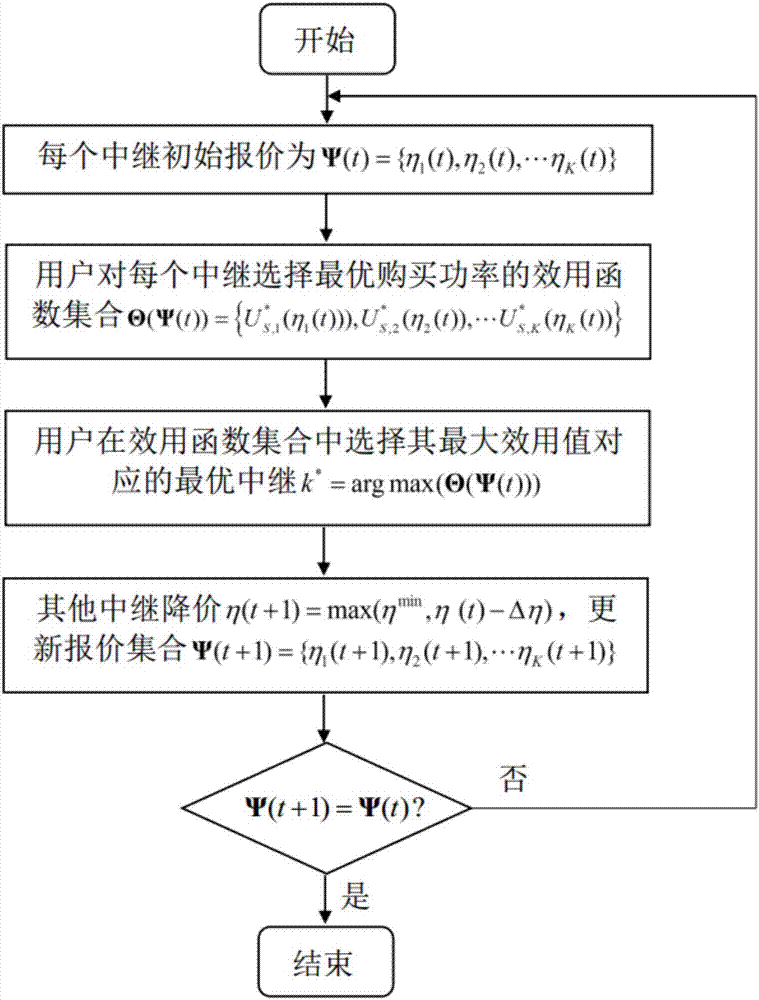
图1是本发明的工作流程图；

图2是本发明中继选择和功率分配方法的程序框图；

图3是本实例中用户效用在用户与中继博弈过程中变化曲线；

图4是本实例中中继价格在用户与中继博弈过程中变化曲线；

图5是本实例中被选择的最优中继随用户位置改变的变化图；

图6是本实例中被选择的最优中继价格随用户位置改变的变化曲线。

具体实施方式

下面结合实施例及附图，对本发明作进一步地详细说明，但本发明的实施方式不限于此。

实施例

一种智能电网中基于博弈论的中继选择和功率分配方法，用于中继网络系统，所述智能电网下的中继网络系统包括一个源节点s、一个目的节点d以及k个中继节点r，核心步骤是用户作为买者以最大效用为准则选择最优中继和最佳购买功率，中继作为卖者由智能电网提供不同的成本价格确定出售价格策略获得最大利润，两者进行博弈，中继在市场中进行竞争，最终两者进行博弈达到平衡，用户和中继节点都根据自身效用最大化而不再改变决策即达到了纳什均衡点。

如图1所示，一种智能电网中基于博弈论的中继选择和功率分配方法，适用于半双工中继网络系统，包括如下步骤：

s1用户在每个数据块传输之前，用户可选择中继协作模式，具体为：用户根据自身效用函数从k个中继节点中选择最合适的中继来建立协作通信链路。每个中继节点的报价为ηk(t)，所有中继构成报价集合为ψ(t)＝{η1(t),η2(t),…ηk(t)}；

在中继网络系统模型中，用户有两种传输模式：直接传输模式和中继协作模式，用户在选择哪种工作模式是由自身的效用函数值大小来进行决定的。

s2用户对每个中继节点k的效用函数为us,k(ηk(t))，在得知每个中继报价集合ψ(t)的条件下，用户对每个中继节点选择最优购买功率pk来使得自身的效用函数达到最大值为用户对k个中继节点组成的效用函数最大值集合用户再从集合θ(ψ(t))选取最大值，其对应的中继节点为最优中继节点k^*＝argmax(θ(ψ(t)))；

s3最优中继k^*的利润函数若被选中继k^*能通过降价出售更多功率来获得更多利润，则更新报价集合ψ(t)＝{η1(t),η2(t),…ηk(t)}，若不降价则报价集合ψ(t)不变；

其他没有被用户选择的中继将进行通过降价来吸引用户，即η(t+1)＝max(η^min,η(t)-△η)，然后得到新的报价集合为ψ(t+1)＝{η1(t+1),η2(t+1),…ηk(t+1)}，如果ψ(t)＝ψ(t+1)则说明中继不再修改报价，用户和中继的策略不再发生变化即达到纳什均衡点，否则返回到s1中。

所述s3具体是中继节点采取行动，被选中中继如果降价卖更多功率使自己利润函数增加则降价，如果不能增加自己利润则不降价；没有被选中的中继进行降价然后得到新的报价集合ψ(t+1)，如果ψ(t)＝ψ(t+1)则不用迭代，否则继续迭代。

在不断博弈迭代之后最终用户对中继的选择、最优功率分配以及中继的报价不再发生变化后，即可认为用户和中继节点不再改变决策即达到了纳什均衡点。本发明实施例的中继选择和功率分配方法的程序框图如图2所示。

本实施例采用的基本场景如下：

协作通信网络中有一个目的节点d位于(0m,0m)，共有四个中继节点ω＝{1,2,3,4}，分别位于(-150m,0m)，(-150m,50m)，(-100m,0m)，(100m,0m)，有一个源节点s从(-300m,0m)移动到(+300m,0m)。噪声功率为10^-8w，信道增益为瑞利衰落其中dij为节点之间的距离，信道衰落因子α为2，中断概率ε为0.001，四个中继节点从智能电网中分别购入的价格分别为{3,1.5,2,2}，中继每次降价的幅度△η为0.2。

本实例的仿真结果使用仿真软件matlab获得。

图3和图4反映了用户在(+130m,0m)时用户与中继之间的博弈，刚开始时候由于用户在选择中继1情况下自身效用最大因此最优中继选择为中继1，其他没有被选择的中继都开始降价来吸引用户，随着价格的下降用户发现选择中继3时自身效用比较大因而开始选择中继3，而中继1、2和4继续降价，最终不断迭代大约75次后，各个中继的价格不再发生变化即开始达到了纳什均衡点从而选择出最优中继，此时也迭代出最优购买功率。

图5和图6反应了用户源节点s从(-300m,0m)移动到(+300m,0m)时候选择中继以及价格变化的情况。在不断移动的过程中用户在选择直接传输模式和中继协作模式的同时也根据不同的情形选择不同位置时刻的最优中继和最优购买功率，其中价格也因中继之间的竞争和智能电网提供不同成本价格而有所不同。

上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受所述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。