基于三级阈值变步长自适应压缩感知技术的信道估计方法与流程

本发明属于信道估计技术领域，具体涉及一种基于三级阈值变步长自适应压缩感知技术的信道估计方法。

背景技术：

正交频分复用(orthogonalfrequencydivisionmultiplexing，ofdm)广泛应用于无线通信领域，因此对ofdm系统进行信道估计成为无线信道的关键技术。传统的信道估计方法在插入导频时需要满足奈奎斯特准则，使得导频插入数量多，并且信道估计的精度较低，因此，信道估计技术引起广泛关注。当前，针对这一问题，有学者提出了基于压缩感知技术的信道估计方案，其借助压缩感知技术能够在较大压缩率下重构出原始稀疏数据信息的原理，以及信道在大部分情况下都具有稀疏性的特点，将压缩感知技术应用在信道估计中。这种方法极大的减少了导频插入的数量，提高了频谱利用率，但是传统的压缩感知算法如omp等，需要以信道的稀疏度为先验信息，这使得其在信道估计中的应用具有局限性。最近有学者提出了将稀疏度自适应的压缩感知算法应用在信道估计中，从而打破了压缩感知在信道估计中需要已知稀疏度的缺陷，但是这种技术的耗时较长，稀疏度估计的精确程度不高。基于压缩感知能够在较大压缩率下进行信道估计的特性以及稀疏度自适应算法的原理，本专利对稀疏度自适应的步长选取方式进行了改进，增强了稀疏度自适应算法步长选取的灵活性，从而提高了稀疏度估计的精确程度，进而提高信道估计的性能。

技术实现要素：

本发明的目的在于提供一种基于三级阈值变步长自适应压缩感知技术的信道估计方法。

本发明的目的是这样实现的：

基于三级阈值变步长自适应压缩感知技术的信道估计方法，包括如下步骤：

步骤1：在信道的数据发送端插入导频，将带有导频的数据信号通过带有加性高斯白噪声的信道模型；

步骤2：在信道接收端获得导频位置的信号信息；

步骤3：设置初始步长，根据发送端和接收端的导频信息利用改进的变步长自适应匹配追踪方法进行初步信道估计；

步骤4：计算估计误差，利用改进的变步长自适应匹配追踪方法中三级阈值确定步长变化的大小，增加步长，得到新的信道稀疏度；

步骤5：循环执行步骤4，直到满足信道估计精度。

所述步骤4中改进的变步长自适应匹配追踪方法具体流程包括：

步骤(4.1)输入观测矩阵a，压缩向量yp，初始步长s；其中a的维数是m×n，yp的维数是m×1，s为正整数；

步骤(4.2)初始化信道估计值残差r0＝yp，支撑集支撑集大小l＝s，迭代次数k＝1；

循环执行步骤(4.3)～(4.12)；

步骤(4.3)计算内积：|ark-1|，取内积最大的l个值对应的原子的序号，存入集合nk，得到候选集ck＝fk-1∪nk；

步骤(4.4)计算取最大的l个值对应的原子的序号，存入支撑集f，计算估计信道计算残差

步骤(4.5)判断是否满足迭代停止条件：其中t1为正常数，表示一级阈值；若满足，执行步骤(4.6)，若不满足，执行步骤(4.8)；

步骤(4.6)判断是否满足迭代停止条件：其中t2为正常数，表示二级阈值；若满足，执行步骤(4.7)，若不满足，执行步骤(4.11)；

步骤(4.7)判断是否满足迭代停止条件：其中t3为正常数，表示三级阈值；若满足，则停止迭代，得到信道估计值若不满足，执行步骤(4.12)；

步骤(4.8)判断是否满足||r||2≥||rk-1||2，若满足，执行步骤(4.9)，若不满足，执行步骤(4.10)；

步骤(4.9)进入下一阶段，支撑集f的大小增大为l＝l+s，迭代次数为k＝k+1；

步骤(4.10)更新支撑集fk＝f，更新残差rk＝r，迭代次数为k＝k+1；

步骤(4.11)进入下一阶段，改变步长支撑集f的大小增大为l＝l+s，迭代次数为k＝k+1；

步骤(4.12)进入下一阶段，改变步长支撑集f的大小增大为l＝l+s，迭代次数为k＝k+1；

步骤(4.13)输出目标稀疏向量

所述步骤2中在信道接收端获得导频位置的信号为yp＝diag(xp)fh+wp＝ah+wp，其中xp为发送端的导频信号，yp为接收端的导频信号，h表示时域信道，f为傅里叶变换矩阵，维数为n×1，wp表示加性高斯白噪声，维数为n×1。

本发明有益效果在于：

(1)采用压缩感知技术，能够突破传统信道估计方式中导频插入需要满足奈奎斯特定理的束缚，减少了导频的插入数量，提高了频带利用率；

(2)采用的新的压缩感知算法—改进的变步长自适应匹配追踪(mvssamp)算法相比较于其他应用于信道估计的压缩感知算法而言信道估计的精确度高；

(3)采用的压缩感知算法步长选取的灵活性高，稀疏度估计的精度高。

附图说明

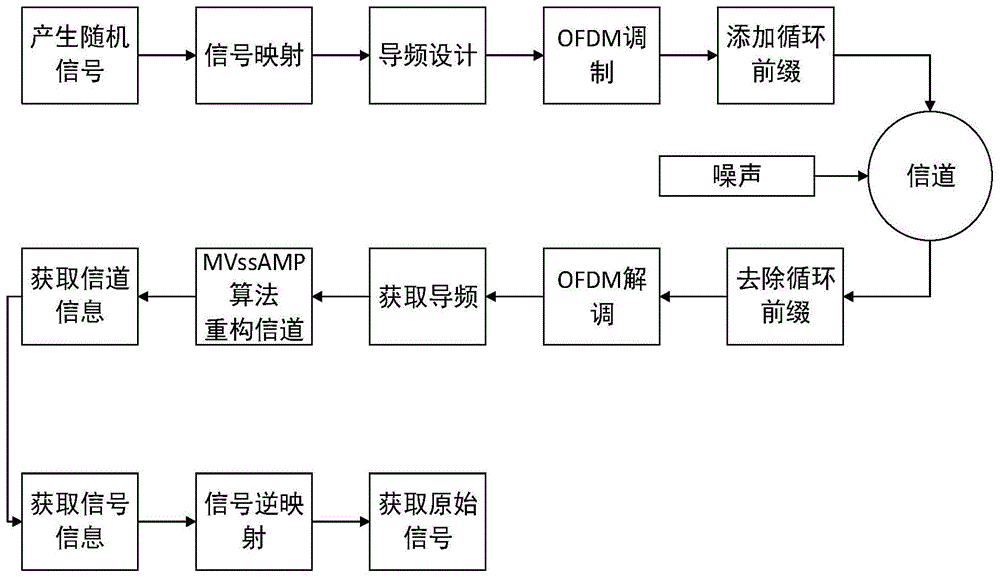
图1为本发明整体实现框图；

图2(a)为本发明实际信道线形效果图；

图2(b)为本发明估计信道线形效果图；

图3(a)为本发明实际信道条形效果图；

图3(b)为本发明估计信道条形效果图；

图4为本发明在不同信噪比条件下的信道估计误差分析；

图5为针对本发明不同信噪比条件下的信号传输误码率分析。

具体实施方式

下面结合方法具体步骤以及附图仿真结果对本发明做更进一步描述。以下实施例用于说明本申请，但不用来限制本申请的范围。

本申请发明针对信道估计效果不佳的情况，提出了一种基于三级阈值变步长自适应压缩感知技术的信道估计方法。本信道估计方案的要点为利用新的压缩感知算法进行稀疏度未知情况下的信道估计。本发明围绕传统信道估计方案的缺点进行改进，利用提出的mvssamp算法进行信道估计，在信道的数据发送端只需要插入少量的导频信息，然后在信道接收端得到相应的输出导频信息，将这些发送的导频信息和接收的导频信息代入mvssamp算法，就能够估计出稀疏信道。这种信道估计方式突破了传统信道估计中导频插入需要满足奈奎斯特准则的束缚，提高了信道估计精确度。

(1)利用压缩感知表示稀疏信道：

在信号经过无线信道进行传输的过程中，接收端接收到的导频信号为

yp＝diag(xp)fh+wp(1-1)

其中，xp是发送端的导频信号，diag(xp)是将xp作为主对角元素的对角矩阵，yp是接收端的导频信号，h是时域信道，wp～n(0,σw²)是频域噪声，σw²是噪声的方差，f是傅里叶变换矩阵。令a＝diag(xp)f，有：

yp＝ah+wp(1-2)

需要注意的是，yp的维数与导频的数目相同，因此，当导频的数目小于信道长度时，式(1-2)为欠定线性方程组。即，稀疏信道估计是欠定线性方程组在稀疏约束下的一个逆解过程。所以，稀疏信道估计问题的关键是如何在噪声条件下精确的求解出上述欠定线性方程组的h。

压缩感知技术解决的问题是如何在高压缩率条件下得到欠定线性方程组的最优解，因此将压缩感知技术应用于信道估计在理论上是可行的。将yp视为压缩感知技术中压缩后的信号，a视为压缩感知技术中的观测矩阵，h视为压缩感知技术中的稀疏解，则根据压缩感知的基本原理，(1-2)式可以表示为：

min||h||0s.t.yp＝ah+wp(1-3)

其中，||h||0表示向量h的l0范数。所以，稀疏信道估计问题转化为式(1-3)的求解问题。

(2)利用提出的mvssamp算法估计稀疏信道：

针对信道估计精确程度不高的问题，采用本文提出的mvssamp算法来进行信道估计过程。mvssamp算法的基本思想是：设定一个初始步长s来作为信道的初始稀疏度(抽头数)，然后利用内积匹配准则计算观测矩阵a与接收导频信号yp的相关性，选择a中与yp相关性最大的s个原子(即观测矩阵a与接收导频信号yp的s个最匹配的原子，其中，原子为a的列向量)形成支撑集，利用最小二乘法计算此时支撑集f下yp对应的信道估计值并据此计算出接收导频信号yp与此在支撑集f下对应的压缩向量之间的残差r。在此基础上，重新利用内积匹配准则计算观测矩阵a与残差r的相关性，选择原子，更新支撑集f，如此循环迭代，直到满足相应的设置条件改变支撑集f的大小。此时，再次循环执行上述步骤，直到满足迭代终止条件为止。迭代终止后，yp在支撑集下对应的即视为最终的信道估计值。通过这个过程，该算法实现了稀疏信道的重建。

在此利用提出的mvssamp算法进行稀疏信道估计的过程中，需要注意以下问题：

a.由于信道的抽头数k是确保信道能够被精确估计的关键，而实际的信道估计过程中信道的抽头数k是未知的，所以在进行信道估计时需要先估计出信道的抽头数k，以达到较好的信道重建效果。在本文提出的mvssamp算法中，先给定一个较小的初始步长s，s为正整数，然后将稀疏信道的迭代重建过程分为多个阶段，每个阶段所对应的支撑集λ的大小l之差即为步长s，在每个阶段中，,稀疏信道重建所需的支撑集λ的大小l不发生改变,通过观测矩阵a和残差r的内积最大的值形成候选集c，再经过迭代从候选集c中选取支撑集λ中的原子。当该支撑集λ的大小l不能满足重建要求时，以步长s来增大它的规模。由此l不断增大，可以在信道稀疏度未知的前提下逼近信道抽头数k。

b.为了在信道估计的过程中获得精确的估计值，需要设置合理的迭代停止条件。根据步长s增大过程中能量差的原理，在步长s逐渐增大但未达到稀疏度时，相邻两个阶段中重建信道的能量差是不断减小的，并且相邻阶段重建信道的能量差在最初的阶段中下降很快，之后下降幅度减小，最后基本上趋于稳定，此时稀疏信道的重建过程完成。为了提高重建精度，缩短重建时间,根据此能量差原理，本文设定了三重阈值：t1，t2，t3，停止迭代条件1、2、3分别对应阈值t1，t2，t3，其中，t1＞t2＞t3。当相邻阶段重建信道的能量差接近阈值t1时，说明算法以大步长迅速接近重建稀疏信道，从而减少重建时间；当相邻阶段重建信道的能量差接近阈值t2时，算法以稍小步长逐渐接近重建稀疏信道，从而由减少重建时间转化为提高重建精度；当相邻阶段重建信道的能量差接近阈值t3时，说明算法以小步长逐渐逼近重建稀疏信道，从而进一步提高重建精度。

c.在信道抽头数未知的前提下，给定一个较小的初始步长，计算该步长下相邻的两次迭代对应的稀疏向量的估计值的能量差，然后设定三级阈值，通过该能量差与三个阈值的关系，判断步长的相应增量，更新步长。该步长更新方式的重点在于通过设定三级阈值，能够使得步长以更加合适的增量增加，这样既能够保证算法执行过程中步长接近于信道抽头数的速度，又能够保证信道估计的精确度。

基于三级阈值变步长自适应压缩感知技术的信道估计方案流程

mvssamp算法流程

针对传统信道估计方案(基于满足奈奎斯特准则的信道估计方案，基于传统压缩感知技术的信道估计方案)存在的不足，提出基于mvssamp算法的信道估计方案。该方法在信道的稀疏度(抽头数)未知的情况下，以信道发送端导频和信道接收端导频为已知条件，给定一个初始步长，然后通过设定三级阈值实现对于步长的有效控制，使得步长能够以合理的速度增大，直到接近真实的信道稀疏度，此时信道的估计精确度也逐渐提升。因此，该算法具有较高信道估计的精确度。此外，该算法是基于压缩感知体制改进的算法，其利用压缩感知技术能够实现大压缩率下稀疏向量的重建的原理，在信道的数据发送端仅仅需要插入少量的导频信号便可以在数据输出端精确的重建出原始稀疏信道，使得导频信号的插入方式突破了奈奎斯特准则的限制，大大节省了频带资源。因此，该算法的运行速度快。通过效果图分析、直方图分析、信噪比分析以及误码率分析等的仿真结果表明本文所提出的信道估计方案具有创新性，可行性和可靠性。

本信道估计方案的性能验证对象为加性高斯白噪声信道。图1展示了本方案的整体实现框图。图2和图3展示了本信道估计方案的估计效果，图2为线形图，图3为条形图，从这两图可以看出，本文采用的信道估计方案效果较佳，验证了本方案的可行性。图4展示了本信道估计方案的抗噪声相关性能的分析，信道估计方法的抗噪声性能的优劣的评价指标主要是在含噪声情况下所使用的算法对于信道估计的准确程度，信道估计的准确程度越高，说明算法的抗噪声性能越好。从该图可以看出，本信道估计方案在含噪条件下的信道估计的相对误差较小，说明利用本方案进行信道估计的准确程度较好，从而说明了本方案所提算法抗噪声能力强。图5展示了本方案的信道估计的精确度。信道估计的精确程度与误码率成反比，从图5可以看出本信道估计方案的误码率很低，说明了本方案的信道估计的精确程度高，具有很好的信道估计效果。综合而言，本文提出的基于三级阈值变步长自适应压缩感知技术的信道估计方案具有创新性，可行性以及可靠性。