复杂小天体表面着陆避障常推力控制方法
本发明涉及一种复杂小天体表面着陆避障常推力控制方法,适用于以常推力为推进方式的小天体着陆器,属于深空探测技术领域。
背景技术:
着陆是小天体探测任务中至关重要的一步,是获取小天体表面有效的科学数据信息的有效保障,也是执行小天体表面样品采集及返回任务的必要前提条件。随着空间科学技术和航天技术的不断发展,小天体探测任务将寻求着在具有更高的科学价值或更多的特殊资源的复杂区域进行着陆,而这些区域往往环境复杂,地形崎岖,山脊、低谷、凹坑和丘陵广泛分布,威胁着陆器的精准安全的着陆任务,致使小天体表面的着陆任务难度增大。因此能够保障着陆器在复杂地形环境中安全着陆的自主避障控制方法是小天体着陆段探测技术的重要研究方向。目前势函数制导法是常用的着陆器的自主避障方法,然而小天体复杂的地形环境会导致势函数制导法产生局部极小值问题,导致着陆器陷入局部极小值区域,无法到达目标着陆点。
在已发展的势函数着陆避障控制方法中,在先技术[1](yuan,x.,etal.,probability-basedhazardavoidanceguidanceforplanetarylanding.actaastronautica,2018.144:p.12-22.),从障碍威胁概率性描述的角度,提出一种基于碰撞概率的着陆避障控制方法,通过计算不确定条件下着陆器与星表障碍的实时碰撞概率,对障碍威胁进行概率性描述,并基于实时碰撞概率推导解析的障碍规避控制律,提高不确定条件下的实时障碍规避能力,并对不确定性条件的实时变化具有适应性,提高了避障控制的鲁棒性与自主着陆安全性。但是该算法未考虑产生的局部极小值问题,在复杂地形下会导致着陆器陷入局部极小值区域,无法到达目标着陆点。
在先技术[2](参见朱圣英等.基于膨胀预警区的小天体着陆避障常推力控制方法:中国,zl202010766827.9[p],2020-08-03),基于着陆障碍区域影响定义膨胀预警区,对传统人工势函数进行改进;将设计的改进人工势函数梯度引入到线性滑模面中,并对人工势函数相应参数进行设计,同时设计适用于常推力发动机的滑模控制律,并引入死区进行控制律改进,实现着陆器在常推力作用下的在复杂区域内飞行时的障碍规避和精准着陆,并增加着陆器的工作寿命。但是该算法同样未未考虑会产生的局部极小值问题,在复杂地形下会导致着陆器陷入局部极小值区域,无法到达目标着陆点。
技术实现要素:
本发明的目的是为了解决现有的势函数制导法会导致着陆器陷入局部极小值区域,无法到达目标着陆点的问题。本发明的方法对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,通过对各个障碍进行合并包围,将复杂障碍地形分割为若干个相互不影响的障碍区域,对复杂障碍地形进行简化,避免多个障碍产生的斥力势函数在某一区域过度叠加产生局部极小值问题。同时定义新型斥力势函数,验证在着陆器、目标点和障碍物危险圆柱在水平方向上对齐且障碍物危险圆柱在两者中间的情况下,着陆器可有效逃离局部极小值点,并最终到达目标着陆点处,最终证明本发明可以有效避免势函数制导法导致着陆器陷入局部极小值区域的问题。
本发明的目的是通过下述技术方案实现的。
本发明公开的复杂小天体表面着陆避障常推力控制方法,建立着陆点固连坐标系下的着陆器动力学方程;采用线性滑模面和改进人工势函数相结合的方法,设计滑模面和引力势函数系数;对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,通过对各个障碍进行合并包围,对着陆障碍进行简化,提出新型斥力势函数,验证在着陆器、目标点和障碍物危险圆柱在水平方向上对齐且障碍物危险圆柱在两者中间的情况下,可有效逃离局部极小值点处;设计并改进常推力控制律;应用复杂小天体表面着陆避障常推力控制方法进行小行星着陆的控制,能够有效避免势函数制导法导致着陆器陷入局部极小值区域的问题,并保证着陆器在常推力作用下的障碍规避和精准着陆。
本发明公开的复杂小天体表面着陆避障常推力控制方法,包括如下步骤:
步骤1:建立小天体的固连坐标系σb和着陆点固连坐标系σl,利用着陆器在σb系下的着陆动力学方程和两个坐标系之间的位置、速度转换关系推导出σl系下的着陆器动力学方程。
步骤1的具体实现方法为:
以小天体质心为原点ob,小天体自旋轴为zb轴,小天体最小惯性轴为xb轴,通过右手法则定义yb轴建立小天体的固连坐标系ob-xbybzb(σb);以目标着陆点为原点ol,ol所在平面外法线方向为zl轴,以位于zlolzb平面并垂直于zl轴指向小天体南极方向为xl轴,通过右手法则定义yl轴建立小天体的着陆点固连坐标系ol-xlylzl(σl)。
着陆器在σb系下的动力学方程为:
其中rb和vb分别为着陆器在σb系下的位置矢量和速度矢量;ω=[0,0,ω]t为小天体自转角速度矢量,假设小天体均匀旋转,即
σb和σl之间,着陆器的位置和速度之间有着如下的坐标转换关系:
其中,rl和vl分别为着陆器在σl系下的位置矢量和速度矢量,lb为
着陆器在σb系下的动力学方程为:
其中,dl为σl系下干扰加速度,acl为σl系下控制加速度。定义由于小天体引力场和自转效应对着陆器着陆动力学产生的影响加速度
将公式(4)代入公式(3)中,并引入控制加速度表达式,得到简化后的着陆动力学方程:
其中,tcl为着陆器自带推力器产生的控制推力矢量,且有tcli∈{-t,0,+t}(i=1,2,3),t为着陆器单轴所产生的推力大小,下标i表示变量x,y,z轴的分量;m为着陆器的质量,g0为地球海平面处的标准引力加速度;isp为推力器比冲。
步骤2:采用线性滑模面和改进人工势函数相结合的方法,设计滑模面,同时设计引力势函数系数。
步骤2具体实现方法为:
在∑l系下期望的着陆目标点的状态向量的表达式为rld=[0,0,0]tm,对rld求导,可得期望的着陆速度的表达式
其中:
在着陆器的着陆控制过程中,为实现着陆器的障碍规避和精准软着陆,往往在控制系统中引入非负标量函数φ描述航天器在着陆过程中的地形障碍信息和相对位置状态信息,目标着陆点处的势函数值最低。φ通常由两部分组成:引力势函数φa和斥力势函数φr。φ的表达式为:
φ=φa+φr(7)
引力势函数用来描述着陆器所在位置与目标着陆点之间的相对位置关系,两者相对距离越远,引力势函数和吸引力数值越大,在吸引力的作用下,着陆器向势能减小的位置运动,并最终收敛到目标着陆点处,当着陆器到达目标着陆点时,引力势函数和吸引力的值全局最小且为0,吸引力不再产生作用,常用的引力势函数形式为二次函数:
其中,kt=diag(kt1;kt2;kt3)为半正定矩阵。
当着陆器在着陆过程中没有受到障碍影响时,此时仅有引力势函数被激活,公式(6)所示的滑模面可以简化为公式(9)所示的线性滑模面:
当着陆器在公式(9)所示的线性滑模面上运动时,
其中,ti为着陆器在线性滑模面运动的时间,
其中,σ0=[(σ1)0,(σ2)0,(σ3)0]为着陆器的初始相对位置,由公式(10)、(11)可知,当着陆器只受到引力作用而在线性滑模面上运动时,各轴的相对位置大小||σi‖和相对速度大小
由于小天体的逃逸速度vescape较小,在小天体的探测任务中,应对着陆器的着陆速度加以严格控制,避免发生逃逸现象。即
步骤3:对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,建立有效规避着陆器陷入局部极小值的斥力势函数形式。
步骤3的具体实现方法为:
采用圆柱将障碍正好包围其中,该包围区域为“危险区域”,即着陆器不可接触的区域;在危险区域以外,预设范围内定义另一圆柱区域,该区域为“膨胀预警区”;所述“膨胀预警区”将“危险区域”包围;在膨胀预警区之外的区域为“安全区”。
当若干个障碍的膨胀预警区相互重叠时,采用圆柱将所有交叠区域包围,将该区域视为整体,即“危险区域”;再在危险区域以外,预设范围内定义另一圆柱区域,该区域为“膨胀预警区”;
当着陆器进入到膨胀预警区时,斥力势函数迅速增大,产生排斥力,推动着陆器远离障碍,直至着陆器进入到安全区飞行时,斥力势函数降为零,障碍对着陆器的飞行不再产生干扰作用,此时着陆器仅受到吸引力的作用,并逐渐收敛到预定的目标着陆点。
当若干个障碍的膨胀预警区相互重叠时,通过对各个障碍进行合并包围,将复杂障碍地形分割为若干个相互不影响的障碍区域,对复杂障碍地形进行简化,进而避免多个障碍产生的斥力势函数在某一区域过度叠加产生局部极小值问题。
斥力势函数φr表示如下:
其中,rlx、rly、rlz表示在着陆点固连坐标系下,当前时刻着陆器的位置。
为了定量地表示斥力势函数φr中各个障碍的影响范围,kja、kjha、kjo和kjho的设计如下:
得到的新型人工势函数形式为:
该斥力势函数形式能够有效规避着陆器陷入局部极小值问题。
步骤4:在步骤2所建立的滑模面和在步骤3所得的势函数基础上,设计适用于常推力发动机的滑模控制律,并引入死区进行控制律改进,以减少频繁切换发动机的推力方向引起的抖振和燃料消耗。
步骤4的具体实现方法为:
控制律的设计为:
其中,sgn为符号函数。
对公式(21)引入死区进行控制律改进:
其中,f(si)t的定义为:
其中,χi(i=1,2,3)和ψi(i=1,2,3)为人为设定的死区阈值,存在ψi<χi(i=1,2,3)均且均为正数,下标t-δt表示前一时刻的控制量。
通过公式(20)-(22)对控制律进行改进,减少频繁切换发动机的推力方向引起的抖振和燃料消耗。
还包括步骤5:应用复杂小天体表面着陆避障常推力控制方法进行小行星着陆的控制,证明其可以有效避免势函数制导法导致着陆器陷入局部极小值区域的问题,并保证着陆器在常推力作用下的障碍规避和精准着陆。
有益效果
本发明公开的复杂小天体表面着陆避障常推力控制方法,对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,通过对各个障碍进行合并包围,对着陆障碍进行简化,提出新型斥力势函数,验证在着陆器、目标点和障碍物危险圆柱在水平方向上对齐且障碍物危险圆柱在两者中间的情况下,可有效逃离局部极小值点处,证明本发明可以有效避免势函数制导法导致着陆器陷入局部极小值区域的问题,并保证着陆器在常推力作用下的障碍规避和精准着陆。
附图说明
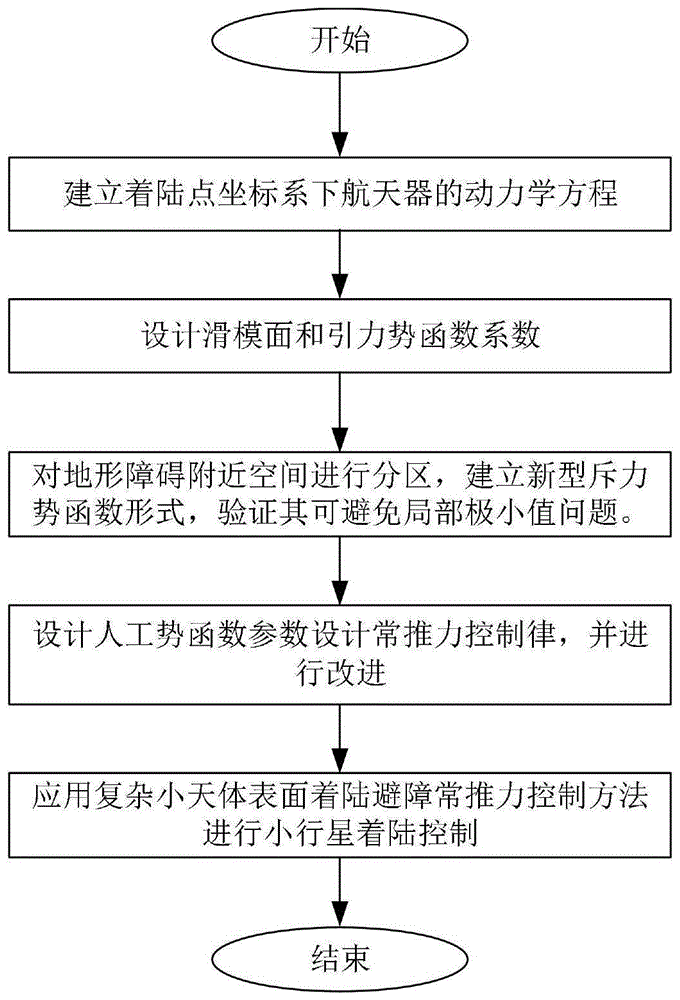
图1是本发明的基于复杂小天体表面着陆避障常推力控制方法流程示意图。
图2是步骤1中小天体的固连坐标系σb和着陆点固连坐标系σl示意图。
图3是步骤3中“危险区”,“膨胀预警区”,“安全区”分区示意图。其中图(a)为基础示意图,图(b)为存在障碍合并情况的基础示意图。
图4是步骤3中局部极小值问题验证的示意图。
图5是步骤5中仿真地形的示意图。
图6是利用高斯势函数制导法的着陆避障轨迹图。
图7是控制方法的仿真分析结果。其中图(a)为着陆器着陆避障轨迹图,图(b)为着陆器三轴位置变化曲线图,图(c)为着陆器三轴速度变化曲线图。
具体实施方式
为了更好的说明本发明的目的和优点,下面结合附图和实例对发明内容做进一步说明。
实施例1:
为了验证本发明的可行性,不规则小行星2063bacchus作为目标天体进行着陆避障控制,采用多面体模型建立小天体引力场,并建立小天体的固连坐标系σb和着陆点固连坐标系σl。该小行星的体积密度为2.0g/cm3,自转周期为14.9h。在σb下,选取的目标着陆点为[130,-210,100]m。在σl系下,着陆器初始位置为[40,40,10]m,初始速度为[0,0,0]m/s,目标终止速度为[0,0,0]m/s,半正定矩阵kt为diag(0.006;0.006;0.002),加权系数为kr=0.002。着陆器的初始质量为m0=200kg,着陆器各轴的推力大小为t=40n,着陆器的比冲为isp=300s。控制律的死区阈值设置为[0.01,0.01,0.01]。
如图1所示,本实施例公开的基于复杂小天体表面着陆避障常推力控制方法,具体实现步骤如下:
步骤1:建立小天体的固连坐标系σb和着陆点固连坐标系σl,利用着陆器在σb系下的着陆动力学方程和两个坐标系之间的位置、速度转换关系推导出σl系下的着陆器动力学方程。
如图2所示建立小天体的固连坐标系σb和着陆点固连坐标系σl,着陆器在σb系下的动力学方程为:
其中rb和vb分别为着陆器在σb系下的位置矢量和速度矢量;ω=[0,0,ω]t为小天体自转角速度矢量,假设小天体均匀旋转,即
σb和σb之间,着陆器的位置和速度之间有着如下的坐标转换关系:
其中,rl和vl分别为着陆器在σl系下的位置矢量和速度矢量,lb为
着陆器在σb系下的动力学方程为:
其中,dl为σl系下干扰加速度,acl为σl系下控制加速度。定义由于小天体引力场和自转效应对着陆器着陆动力学产生的影响加速度
将公式(26)代入公式(25)中,并引入控制加速度表达式,得到简化后的着陆动力学方程:
其中,tcl为着陆器自带推力器产生的控制推力矢量,且有tcli∈{-t,0,+t}(i=1,2,3),t为着陆器单轴所产生的推力大小,下标i表示变量x,y,z轴的分量;m为着陆器的质量,g0为地球海平面处的标准引力加速度;isp为推力器比冲。
步骤2:采用线性滑模面和改进人工势函数相结合的方法,设计滑模面,同时设计引力势函数系数。
在∑l系下期望的着陆目标点的状态向量的表达式为rld=[0,0,0]tm,对rld求导,可得期望的着陆速度的表达式
其中:
人工势函数φ通常由两部分组成:引力势函数φa和斥力势函数φr。φ的表达式为:
φ=φa+φr(29)
当着陆器到达目标着陆点时,引力势函数和吸引力最小且为0,常用的引力势函数形式为二次函数:
其中,kt=diag(kt1;kt2;kt3)为半正定矩阵。
在着陆器着陆之前,需要使着陆器在水平方向抵达期望位置,以防着陆器在着陆过程中与小天体地面相撞,因此z轴的收敛速度应该慢于其他两个轴,即
由于小天体的逃逸速度vescape较小,在小天体的探测任务中,应对着陆器的着陆速度加以严格控制,避免发生逃逸现象。即
步骤3:对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,建立新型斥力势函数形式,并验证其可避免局部极小值问题。
如图3(a)(b)所示,对地形障碍附近空间进行“危险区”,“膨胀预警区”,“安全区”分区,将复杂障碍地形分割为若干个相互不影响的障碍区域,对复杂障碍地形进行简化。基于定义的膨胀预警区对传统的斥力势函数进行改进,改进后得到的斥力势函数φr的公式为:
其中,rlx、rly、rlz表示在着陆点固连坐标系下,当前时刻着陆器的位置。
为了定量地表示斥力势函数φr中各个障碍的影响范围,kja、kjha、kjo和kjho的设计如下:
改进后的人工势函数形式为:
如图4所示,将复杂障碍地形分割后,局部极小值点仅可能发生在着陆器、目标点和障碍物危险圆柱在水平方向上对齐且障碍物危险圆柱在两者中间的情况下。
对于水平方向,公式(38)可以简化为:
假设障碍的水平中心坐标为(x1o,y1o),局部极小值点可能出现的位置为
故存在
由二元函数取极值的条件可知,对于
将公式(40)代入公式(41)可求得kt1=kt2,求二阶导,可得:
联立(40)—(44),可得,ac-b2<0,由二元函数取极值的条件可知,
步骤4:在步骤2所建立的滑模面和在步骤3所设计的势函数基础上,设计适用于常推力发动机的滑模控制律,并引入死区进行控制律改进,以减少频繁切换发动机的推力方向引起的抖振和燃料消耗。
控制律的设计为:
其中,sgn为符号函数。
对公式(45)引入死区进行控制律改进:
其中,f(si)t的定义为:
其中,χi(i=1,2,3)和ψi(i=1,2,3)为人为设定的死区阈值,存在ψi<χi(i=1,2,3)均且均为正数,下标t-δt表示前一时刻的控制量。
通过公式(45)-(47)对控制律进行改进,减少频繁切换发动机的推力方向引起的抖振和燃料消耗。
还包括步骤5:应用复杂小天体表面着陆避障常推力控制方法进行小行星着陆的控制,证明其可以有效避免势函数制导法导致着陆器陷入局部极小值区域的问题,并保证着陆器在常推力作用下的障碍规避和精准着陆。
建立如图5所示仿真着陆区地形障碍三维图,在给定初始条件、末端条件下,利用势函数制导法和复杂小天体表面着陆避障常推力控制方法分别对着陆器进行控制,在图5所示给定的具有特殊地形障碍的仿真着陆区进行着陆,最终仿真结果如图6和图7所示,表明势函数制导法导致着陆器最终陷入极小值区域,而复杂小天体表面着陆避障常推力控制方法实现着陆器有效逃离极小值区域并在着陆过程中成功实现障碍规避,同时速度和位置都收敛于对应的目标值,实现精准着陆。
以上所述的具体描述,对发明的目的、技术方案和有益效果进行了进一步详细说明,所应理解的是,以上所述仅为本发明的具体实施例而已,并不用于限定本发明的保护范围,凡在本发明的精神和原则之内,所做的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!