影响医学结局变量关键分子的筛选方法、系统、终端和存储介质

1.本发明涉及高通量测序领域，特别是涉及一种基于高通量测序数据筛选影响医学中的结局变量的关键分子的算法。


背景技术：

2.随着高通量测序技术(high
‑
throughput sequencing technology)的发展，借助高通量测序的技术手段，探索发育进程、肿瘤发生已经日益普遍。高通量测序技术主要包括基因组测序、转录组测序、蛋白质组测序、修饰蛋白质组测序以及代谢组测序。高通量测序数据是对遗传信息的横断面解析，反映的是生物体在某个时间点上所有遗传物质的突变、修饰或者表达状况。例如人的高通量测序就是对人体所有基因在某个时间点上的分析，因此，高通量测序将产生巨量的数据。对测序数据进行深入、正确的分析是生物信息学家面临的重要课题。借助计算机的强大算力对高通量测序数据进行解析是目前生物信息学发展的主要方式。面对高通量测序数据，分析的方向主要由两个：聚类和降维。聚类的思想是把具有类似模式的样本聚集在一起，从而实现对样本亚群的新认知；降维的思想是将数据从高通量的“高维”降低到关键分子(包括dna、rna和蛋白质)的“低维”，从大量数据中筛选出关键分子，用于后续的分析。目前，降维的方法主要依靠公共数据库的注释，但是并没有出现对于医学中的某个特定结局变量(例如，患者复发与否、患者死亡与否、药物敏感性等)有显著且稳定影响的数据的降维方法。


技术实现要素：

3.为了克服现有技术中的没有出现对于医学中的某个特定结局变量有稳定影响的数据的降维方法的技术缺陷，本发明的第一个方面提供了一种影响医学结局变量关键分子的筛选方法，包括以下步骤：
4.步骤s1：生成随机分层样本表，具体包括以下步骤：
5.步骤s1.1：对全部样本进行样本分层：根据医学中的结局变量的不同，将全部样本集合s划分为子集s1，s2，...，s
n
，全部样本的总数量大于50；
6.s＝s1∪s2∪...∪sn，|s|＞50
7.其中，s1，s2，...，s
n
之间两两互斥；
8.步骤s1.2：进行多次有放回分层随机取样：在步骤s1.1之后，对于每一层进行随机取样，每一次分层随机取样的样本数量n的计算公式为：
9.n＝k1×
r+k2×
r+
……
+k
n
×
r
10.其中，r为每一个子样本层的每次取样的比例，分层随机取样的总次数m≥100次，最终生成随机分层样本表；
11.步骤s2：分别对每一次分层随机取样获得的抽取样本进行回归分析：
12.对于医学中的与时间有关的结局变量，采用cox比例风险回归，cox比例风险回归
的计算公式为：
13.ln[h(t，x)/h0(t)]＝ln rr＝β1x1+β2x2+
…
+β
m
x
m
[0014]
其中，h(t，x)为t时刻发生x事件的危险度；h0(t)表示所有协变量取值为0时的风险函数，也称为基准风险函数；rr表示相对危险度；x1，x2，...，x
m
分别为影响x事件发生的协变量；β1、β2、β
m
分别为协变量系数，负值表示x事件的保护因素，正值表示x事件的危险因素，其绝对值表示对x事件影响力的大小，采用常规log
‑
rank方法计算p值；
[0015]
对于医学中的与时间无关的二分类结局变量，采用logistic回归，logistic回归的计算公式为：
[0016]
logitp＝α+β1x1+β2x2+
…
+β
m
x
m
[0017]
其中，p为结局变量的发生概率，α是为了使得等式成立而由计算得出的常数项，x1，x2，...，x
m
为协变量；β1、β2、β
m
分别为协变量系数；
[0018]
步骤s3：筛选出对医学中的结局变量有显著影响的关键分子：对于步骤s2中的分层随机取样获得的抽取样本进行m次回归分析，对回归结果进行log
‑
rank检验得到p值，分别记为p1，p2，p3，...，p
m
，以p＜0.05为统计有显著意义，筛选出在至少75％的抽样次数中均有显著意义的关键分子，即得对医学中的结局变量有显著影响的关键分子；
[0019]
步骤s4：筛选出对医学中的结局变量有显著且稳定影响的关键分子：统计结果有意义的次数n，以稳定系数γ表示自变量x(自变量x是指不同的关键分子)对结局变量y影响的稳定程度，则自变量x对结局变量y影响的稳定系数γ为：
[0020][0021]
然后按照稳定系数γ的大小，将在至少75％的抽样次数中均有显著意义的关键分子进行降序排列，从而筛选出对医学中的结局变量有显著且稳定影响的关键分子。
[0022]
进一步地，步骤s1进一步包括：
[0023]
步骤s1.3：可视化所述随机分层样本表：使用基于r语言的pheatmap函数展示每次参与回归分析的样本；并使用基于r语言的ggplot2函数展示每个样本参与回归分析的频率。
[0024]
进一步地，在步骤s1.2中，每一个子样本层的每次取样的比例r为50％～90％。
[0025]
进一步地，所述关键分子选自dna、rna、蛋白质中的任一种或两种以上。
[0026]
本发明的第二个方面提供一种影响医学中的结局变量的关键分子的筛选系统，包括：随机分层样本表生成模块、回归分析模块和筛选模块；
[0027]
所述随机分层样本表生成模块包括分层模块和取样模块，
[0028]
所述分层模块用于对全部样本进行样本分层：根据医学中的结局变量的不同，将全部样本集合s划分为子集s1，s2，...，s
n
，全部样本的总数量大于50；
[0029]
s＝s1∪s2∪...∪sn，|s|＞50
[0030]
其中，s1，s2，...，s
n
之间两两互斥；
[0031]
所述取样模块用于进行多次有放回的分层随机取样：在步骤s11之后，对于每一层进行随机取样，每一次分层随机取样的样本数量n的计算公式为：
[0032]
n＝k1×
r+k2×
r+
……
+k
n
×
r
[0033]
其中，r为每一个子样本层的每次取样的比例，分层随机取样的总次数m≥100次，
最终生成随机分层样本表；
[0034]
所述回归分析模块用于分别对每一次分层随机取样获得的抽取样本进行回归分析：
[0035]
对于医学中的与时间有关的结局变量，采用cox比例风险回归，cox比例风险回归的计算公式为：
[0036]
ln[h(t，x)/h0(t)]＝ln rr＝β1x1+β2x2+
…
+β
m
x
m
[0037]
其中，h(t，x)为t时刻发生x事件的危险度；h0(t)表示所有协变量取值为0时的风险函数，也称为基准风险函数；rr表示相对危险度；x1，x2，...，x
m
分别为影响x事件发生的协变量；β1、β2、β
m
分别为协变量系数，负值表示x事件的保护因素，正值表示x事件的危险因素，其绝对值表示对x事件影响力的大小，采用常规log
‑
rank方法计算p值；
[0038]
对于医学中的与时间无关的二分类结局变量，采用logistic回归，logistic回归的计算公式为：
[0039]
logitp＝α+β1x1+β2x2+
…
+β
m
x
m
[0040]
其中，p为结局变量的发生概率，α是为了使得等式成立而由计算得出的常数项，x1，x2，...，x
m
为协变量；β1、β2、β
m
分别为协变量系数；
[0041]
所述筛选模块用于筛选出对医学中的结局变量有显著影响的关键分子：对于步骤s2中的分层随机取样获得的抽取样本进行m次回归分析，对回归结果进行log
‑
rank检验得到p值，分别记为p1，p2，p3，...，p
m
，以p＜0.05为统计有显著意义，筛选出在至少75％的抽样次数中均有显著意义的关键分子，即得对医学中的结局变量有显著影响的关键分子；
[0042]
所述筛选模块还用于筛选出对医学中的结局变量有显著且稳定影响的关键分子：统计结果有意义的次数n，以稳定系数γ表示自变量x对结局变量y影响的稳定程度，则自变量x对结局变量y影响的稳定系数γ为：
[0043][0044]
然后按照稳定系数γ的大小，将在至少75％的抽样次数中均有显著意义的关键分子进行降序排列，从而筛选出对医学中的结局变量有显著且稳定影响的关键分子。
[0045]
进一步地，所述影响医学中的结局变量的关键分子的筛选系统进一步包括可视化模块，所述可视化模块用于可视化所述随机分层样本表：使用基于r语言的pheatmap函数展示每次参与回归分析的样本；并使用基于r语言的ggplot2函数展示每个样本参与回归分析的频率。
[0046]
进一步地，每一个子样本层的每次取样的比例r为50％～90％。
[0047]
进一步地，所述关键分子选自dna、rna、蛋白质中的任一种或两种以上。
[0048]
本发明的第三个方面提供一种智能终端，包括：
[0049]
存储器，所述存储器用于存储可执行程序代码；以及
[0050]
处理器，所述处理器用于读取所述存储器中存储的可执行程序代码以执行上述影响医学中的结局变量的关键分子的筛选方法。
[0051]
所述智能终端包括但不限于pc、便携计算机、移动终端等具有显示和处理功能的设备。
[0052]
本发明的第四个方面提供一种计算机可读存储介质，所述计算机可读存储介质上
存储有计算机程序指令，所述计算机程序指令被处理器执行时，实现上述影响医学中的结局变量的关键分子的筛选方法。所述计算机可读存储介质包括但不限于：u盘、移动硬盘、只读存储器(rom，read
‑
onlymemory)、随机存取存储器(ram，randomaccessmemory)、磁碟或者光盘等各种可以存储程序代码的介质。
[0053]
采用了上述技术方案后，与现有技术相比，具有以下有益效果：
[0054]
本技术提供了一种新的计算机算法，即通过多次有放回分层随机取样的回归算法，能够实现高通测序数据的降维，能够精准地筛选出在高通量测序数据对特定的结局变量(包括但不限于疾病复发或者不复发、用药敏感或者不敏感、患者死亡或者生存等结局变量)有显著影响的关键分子(包括dna、rna和蛋白质)。除此之外，本技术的算法还提供了一种简洁有效地评价回归模型稳定性的方法，实现了关键分子的稳定性评价，即通过计算自变量x的稳定系数γ来评价自变量对结局变量/事件影响的稳定性大小，实现了对关键分子稳定性的量化。本技术的技术方案有助于解决医学中回归模型不稳定且重复性差的技术难题，并提高测序高通量大数据的临床转化效率，有助于推动生物信息学的进步和发展。本发明利用回归的方法，设计了利用多次回归的方法筛选高通量测序数据中关键基因筛选算法，实现了从高通量数据中筛选出对结局变量有影响的关键基因，为下游的功能研究和机制研究奠定基础。
附图说明
[0055]
图1为在本技术一实施例中，对随机分层样本表进行可视化后的热图，x轴表示用于回归分析的次序，用数字1
‑
100表示；y轴表示每个样本的名称(样本名称从左到右依次为：tcga
‑
w5
‑
aa2q，tcga
‑
zu
‑
a8s4，12t，3t，tcga
‑
zd
‑
a8i3，tcga
‑
w5
‑
aa39，20t，30t，10t，tcga
‑
3x
‑
aav9，tcga
‑
zh
‑
a8y1，tcga
‑
3x
‑
aavb，tcga
‑
4g
‑
aazt，2t，tcga
‑
3x
‑
aava，tcga
‑
zh
‑
a8y6，11t，4t，tcga
‑
w5
‑
aa34，29t，7t，14t，tcga
‑
zh
‑
a8y8，tcga
‑
w5
‑
aa2u，tcga
‑
w5
‑
aa2o，28t，tcga
‑
3x
‑
aave，27t，tcga
‑
zh
‑
a8y2，tcga
‑
3x
‑
aavc，5t，tcga
‑
zh
‑
a8y4，15t，26t，25t，18t，tcga
‑
w6
‑
aa0s，17t，24t，19t，tcga
‑
w5
‑
aa2w，tcga
‑
w5
‑
aa2h，22t，21t，13t，tcga
‑
w5
‑
aa30，tcga
‑
4g
‑
aazo，tcga
‑
w5
‑
aa2t，tcga
‑
zh
‑
a8y5，31t，tcga
‑
w5
‑
aa36，tcga
‑
w5
‑
aa33，16t，tcga
‑
w5
‑
aa38，tcga
‑
w5
‑
aa2r，tcga
‑
w5
‑
aa2z，8t，tcga
‑
w5
‑
aa2i，tcga
‑
w5
‑
aa2g，6t，1t)；热图中黑色表示该样本参与该次回归，灰色表示该样本不参与该次回归；
[0056]
图2为在本技术一实施例中，对随机分层样本表进行可视化后的柱状图，x轴表示每个样本的名称；y轴表示该样本的参与回归分析的频率。本次测试中共进行了100次抽样，每次抽取75％的样本数进行回归分析。
具体实施方式
[0057]
以下结合附图与具体实施例进一步阐述本发明的优点。本领域技术人员应当理解，下面所具体描述的内容是说明性的而非限制性的，不应以此限制本发明的保护范围。
[0058]
应当理解，尽管在本公开可能采用术语第一、第二、第三等来描述各种信息，但这些信息不应限于这些术语。这些术语仅用来将同一类型的信息彼此区分开。取决于语境，如在此所使用的词语“如果”可以被解释成为“在
……
时”或“当
……
时”或“响应于确定”。
[0059]
在后续的描述中，使用用于表示元件的诸如“模块”、“部件”或“单元”的后缀仅为
了有利于本发明的说明，其本身并没有特定的意义。因此，“模块”与“部件”可以混合地使用。
[0060]
实施例1筛选对胆管癌患者无瘤生存时长有显著且稳定影响的长链非编码rna
[0061]
以cox比例风险回归为例，从61个胆管癌转录组测序样本中筛选到927个在胆管癌组织中显著高表达的长链非编码rna，在其基因表达量矩阵(tpm表达矩阵，矩阵的行为基因名称，列为样本名称，矩阵中为基因在样本中的表达量)中，筛选对胆管癌患者无瘤生存时长有显著且稳定影响的长链非编码rna(即关键分子)。
[0062]
在某一个智能终端的存储器存储有可执行程序代码，智能终端的处理器读取所述存储器中存储的可执行程序代码以执行下述影响医学中的结局变量的关键分子(即长链非编码rna)的筛选方法，包括以下步骤：
[0063]
步骤s1：生成随机分层样本表，具体包括以下步骤：
[0064]
步骤s1.1：对全部样本进行样本分层：根据医学中的结局变量的不同，将全部样本集合s划分为子集s1,s2,
…
,s
n
，全部样本的总数量大于50；
[0065]
s＝s1∪s2∪
…
∪sn,|s|>50
[0066]
其中，s1,s2,
…
,s
n
之间两两互斥；
[0067]
步骤s1.2：进行多次有放回的分层随机取样：在步骤s1.1之后，对于每一层进行随机取样，每一次分层随机取样的样本数量n的计算公式为：
[0068]
n＝k1×
r+k2×
r+
……
+k
n
×
r
[0069]
其中，r为每一个子样本层的每次取样的比例，分层随机取样的总次数m≥100次，最终生成随机分层样本表，r为50％～90％；
[0070]
步骤s1.3：可视化所述随机分层样本表：使用基于r语言的pheatmap函数展示每次参与回归分析的样本；并使用基于r语言的ggplot2函数展示每个样本参与回归分析的频率。
[0071]
pheatmap函数的参数设置如下：
[0072]
pheatmap(myindex,color＝c('#2a93d4','#d11c16'),
[0073]
border_color＝'#040000',cluster_rows＝f,
[0074]
legend＝f,
[0075]
cluster_cols＝f,angle_col＝0,
[0076]
fontsize_col＝11,fontsize_row＝8,
[0077]
main＝"",
[0078]
width＝10,height＝6)
[0079]
其中，myindex表示要可视化的样本表；color＝c('#2a93d4','#d11c16')表示可视化的颜色；border_color＝'#040000'表示边框颜色；cluster_rows＝f表示不进行行聚类；legend＝f表示无图例；cluster_cols＝f表示不进行列聚类；angle_col＝0表示label的角度为0度；fontsize_col＝11,fontsize_row＝8表示字体大小；main＝""表示无图标题；width＝10,height＝6表示图大小。
[0080]
ggplot2函数参数设置如下：
[0081]
ggplot(data＝anno,aes(x＝row.names(anno),y＝anno$freq))+
[0082]
geom_hline(yintercept＝c(65,70,75,80),color＝'black',linetype＝8)+
[0083]
geom_bar(stat＝'identity',width＝1.00,fill＝'#ff8a5c',color＝'black')+
[0084]
theme_classic()+
[0085]
scale_y_continuous(expand＝c(0,0),breaks＝c(65,70,75,80))+
[0086]
ylab(label＝'freq')+xlab(label＝null)+
[0087]
theme(axis.text.y＝element_text(face＝'bold',size＝8,colour＝'black'))+scale_x_discrete(labels＝row.names(anno))+
[0088]
theme(axis.text.x＝element_text(face＝'bold',size＝6,colour＝'black',angle＝45,hjust＝1.0,vjust＝1.0))
[0089]
其中，data＝anno表示每次进行抽样的样本个数所组成的数据框；aes(x＝row.names(anno),y＝anno$freq)表示x轴为每次抽样(为1
‑
100个数字)，anno$freq表示每次抽样的频数；geom_hline(yintercept＝c(65,70,75,80),color＝'black',linetype＝8)表示在65,70,75和80的位置绘制横线作为对照，颜色为黑色，横线类型为8(虚线)；geom_bar(stat＝
′
identity
′
，width＝1.00，fill＝
′
#ff8a5c
′
，color＝
′
black
′
)表示直方图的参数，其中直方图宽度为1，填充的颜色为#ff8a5c，描边颜色为黑色；theme_classic()表示我们用的绘图主题；scale_y_continuous(expand＝c(0，0)，breaks＝c(65，70，75，80))表示y轴的起始点为0点，并标注65，70，75，80四个值所在的位置，与前横线相对应；ylab(label＝
′
freq
′
)+xlab(label＝null)表示y轴的标签为freq，横轴标签为空；theme(axis.text.y＝element_text(face＝
′
bold
′
，size＝8，colour＝
′
black
′
))+scale_x_discrete(labels＝row.names(anno))表示y轴标签的字体参数；theme(axis.text.x＝element_text(face＝
′
bold
′
，size＝6，colour＝
′
black
′
，angle＝45，hjust＝1.0，vjust＝1.0))表示x轴的字体参数。
[0090]
步骤s2：分别对每一次分层随机取样获得的抽取样本进行回归分析：
[0091]
对于医学中的与时间有关的结局变量，采用cox比例风险回归，cox比例风险回归的计算公式为：
[0092]
ln[h(t，x)/h0(t)]＝ln rr＝β1x1+β2x2+
…
+β
m
x
m
[0093]
其中，h(t，x)为t时刻发生x事件的危险度；h0(t)表示所有协变量取值为0时的风险函数，也称为基准风险函数；rr表示相对危险度；x1，x2，...，x
m
分别为影响x事件发生的协变量；β1、β2、β
m
分别为协变量系数，负值表示x事件的保护因素，正值表示x事件的危险因素，其绝对值表示对x事件影响力的大小，采用常规log
‑
rank方法计算p值；
[0094]
对于医学中的与时间无关的二分类结局变量，采用logistic回归，logistic回归的计算公式为：
[0095]
logitp＝α+β1x1+β2x2+
…
+β
m
x
m
[0096]
其中，p为结局变量的发生概率，α是为了使得等式成立而由计算得出的常数项，x1，x2，...，x
m
为协变量；β1、β2、β
m
分别为协变量系数。
[0097]
步骤s3：筛选出对医学中的结局变量有显著影响的关键分子：对于步骤s2中的分层随机取样获得的抽取样本进行m次回归分析，对回归结果进行log
‑
rank检验得到p值，分别记为p1，p2，p3，...，p
m
，以p＜0.05为统计有显著意义，筛选出在至少75％的抽样次数中均有显著意义的关键分子，即得对医学中的结局变量有显著影响的关键分子；
[0098]
步骤s4：筛选出对医学中的结局变量有显著且稳定影响的关键分子：统计结果有意义的次数n，以稳定系数γ表示自变量x对结局变量y影响的稳定程度，则自变量x对结局变量y影响的稳定系数γ为：
[0099][0100]
然后按照稳定系数γ的大小，将在至少75％的抽样次数中均有显著意义的关键分子进行降序排列，从而筛选出对医学中的结局变量有显著且稳定影响的关键分子。
[0101]
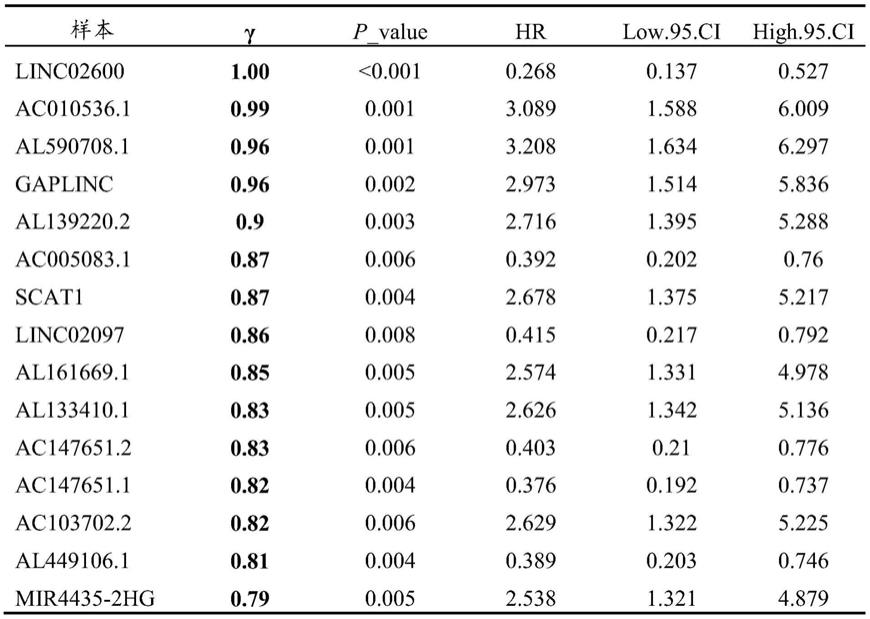
对61个样本进行有放回的分层抽样100次，通过cox回归计算每次抽样样本中927个长链非编码rna的表达对胆管癌患者无瘤生存的影响，以p<0.05为有显著统计学意义，筛选在至少75％的抽样次数中均有意义的长链非编码rna，最后按照稳定系数γ的大小进行降序排列，结果如表1，从而筛选出对医学中的结局变量有显著且稳定影响的关键分子，即从927个在胆管癌组织高表达的长链非编码rna中筛选对胆管癌患者无瘤生存有显著且稳定影响的长链非编码rna。表1中所有样本的长链非编码rna序列均为已知，详见网址：https://portal.gdc.cancer.gov/；https://www.ncbi.nlm.nih.gov/geo/。表1中的γ表示稳定系数，p_value表示p值，rr表示相对危险度，low.95.ci表示相对危险度95％可信区间的下限，high.95.ci表示相对危险度95％可信区间的上限。
[0102]
表1按照γ降序排列的对胆管癌患者无瘤生存有显著且稳定影响的长链非编码rna
[0103][0104]
本领域内的技术人员应明白，本发明的实施例可提供为计算机程序产品、系统、智能终端或计算机可读存储介质。因此，本发明可采用完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本发明可采用在一个或多个其中包含有计算机可执行程序代码(计算机程序指令)的计算机可读存储介质(包括但不限于磁盘存储器、cd
‑
rom、光学存储器
等)上实施的计算机程序产品的形式，该计算机程序产品存储在一个存储介质中，包括若干指令用以使得一台计算机设备(可以是个人计算机，服务器，或者网络设备等)或处理器执行本技术所述方法的全部或部分步骤。而前述的存储介质包括：u盘、移动硬盘、只读存储器(rom，read
‑
onlymemory)、随机存取存储器(ram，randomaccessmemory)、磁碟或者光盘等各种可以存储程序代码的介质。
[0105]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现本技术的影响医学中的结局变量的关键分子的筛选方法中的全部或部分步骤的功能。
[0106]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现本技术的影响医学中的结局变量的关键分子的筛选方法中的全部或部分步骤的功能。
[0107]
应当注意的是，本发明的实施例有较佳的实施性，且并非对本发明作任何形式的限制，任何熟悉该领域的技术人员可能利用上述揭示的技术内容变更或修饰为等同的有效实施例，但凡未脱离本发明技术方案的内容，依据本发明的技术实质对以上实施例所作的任何修改或等同变化及修饰，均仍属于本发明技术方案的范围内。