基于瞬态分形计算和类二维正态分布拟合的冲击定位方法与流程

本发明属于结构健康监测的冲击监测领域，具体提出了一种基于瞬态分形计算和类二维正态分布拟合的冲击载荷定位方法。

背景技术：

早期冲击定位识别方法主要是通过提取冲击应力波的到达时间，根据距离、时间、应力波波速三者之间的关系来计算出冲击的位置信息。但是在实际情况中，应力波的波达时间提取易受噪声的影响。后来有学者利用小波分析的方法对信号进行频域处理，减小了噪声的影响，提取了波达时间，对距离、时间、波速方程进行了优化，获得了冲击的位置信息。

基于光纤FBG传感器的冲击载荷定位方法虽然有很多优点，但其采样速率较低，存在以下不足。

首先，现有的光纤FBG传感器冲击载荷定位方法在传感器布局方式上大多采用正方形布局。此布局方法只能对传感器所围成的区域内进行监测，应用于大面积板结构冲击时在布局上有效利用率较低，因此急需研究有助于提高传感器布局的监测效率的方法。

其次，现有的光纤传感器冲击载荷定位特征信息提取方法大都是采用FFT、小波分解处理方法，这些信号提取方法都在一定程度上忽略了样本点信号采集时所产生的误差，使得处理结果不够准确。而通过提取冲击响应信号特征信息，采用先验方法如神经网络方法确定冲击的位置信息的方法，又存在需要大量不同的冲击情况来训练网络，泛化性能不好，实用性和实时性均不强等缺点。因此，需要研究有助于提高信号纯度，减少实验误差的方法。

此外，现有的光纤传感器特征信号处理方法大多数只能表征光纤FBG传感器在某一条线上或者某一部分中的特征。为了提高冲击载荷辨识速度，需要研究能够表征光纤FBG传感器在监测区域内的特征模型。

最后，针对时差法、神经网络、支持向量机辨识这些冲击载荷位置识别方法的不足，本发明提出了一种基于瞬态分形计算和类二维正态分布拟合的冲击定位方法。

技术实现要素：

技术问题：本发明提供了一种有助于提高效率的冲击载荷位置辨识方法，该方法采用基于六边形蜂窝布局的光纤FBG传感网络配置方法，通过瞬态分形计算的方式提取冲击响应信号的特征信息，利用特征信息和类二维正态分布曲面的高度契合特性进行曲面拟合，适用于大面积薄板类结构，该方法在监测面积一定的情况下有助于有效减少光纤FBG传感器数量，降低系统复杂程度。

技术方案：为解决上述技术问题，本发明基于瞬态分形计算和类二维正态分布拟合的瞬时载荷定位，包括下列步骤：

步骤一：蜂窝结构监测网络布置及相应监测区域划分

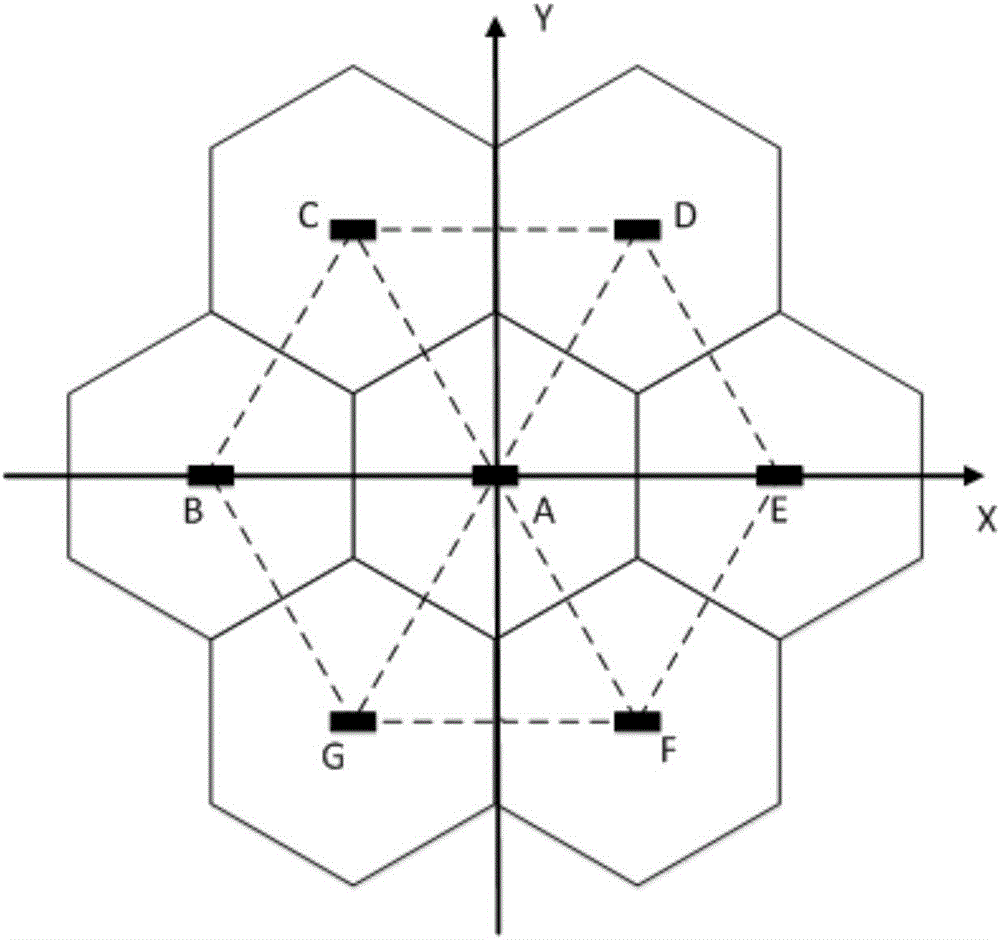
将监测区域划分为七个相同的正六边形结构区域，并连接成蜂窝形状，即中间一个正六边形，周围六个正六边形；每个正六边形的正中心横向布置一个光纤FBG传感器，位于中间的光纤传感器记作传感器A，其余的延顺时针方向依次记作传感器B、C、D、E、F、G；

将中间的正六边形视作六个正三角形区，将每个正三角形，以及与其相邻的正六边形合起来作为一个监测区域，整个监测区域分为六个监测子区域，分别为监测子区域Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ；

其中传感器A和传感器B监测子区域Ⅰ；传感器A和传感器C监测子区域Ⅱ；传感器A和传感器D监测子区域Ⅲ；传感器A和传感器E监测子区域Ⅳ；传感器A和传感器F监测子区域Ⅴ；传感器A和传感器G监测子区域Ⅵ；

步骤二：冲击样本点选取规则与冲击响应信号采集

(2-1)、在结构试件的冲击待监测区域上建立一个二维直角坐标系，以光纤光栅传感器A和E连线方向作为x轴正方向，以光纤光栅传感器A和B连线方向作为x轴负方向，以光纤光栅传感器A和传感器C、D中点连线方向作为y轴正方向，以光纤光栅传感器A和传感器F和G中点连线方向作为y轴负方向；冲击样本点选取规则为：在每两个相邻传感器连线上均匀取点，并以这些点作为冲击样本点；

(2-2)、然后利用冲击锤采用相同能量大小对这些冲击样本点依次进行冲击；分别记录每次冲击下，分布式光纤传感网络的冲击响应信号；将每次冲击下的分布式光纤传感网络的冲击响应信号称为一组冲击响应信号；每组冲击响应信号包括七个传感器的相应冲击响应信号，即七个传感器的中心波长偏移量；

步骤三：基于瞬态分形计算的冲击响应特征信息提取

依次对步骤二所得的每一组冲击响应信号进行特征信息提取，即首先采用瞬态分形计算方法对冲击响应信号进行预处理。瞬态分形计算方法是基于分形维数的一种算法，此方法利用瞬时分形量具对时域信号进行处理，可以提高信号纯度；具体体过程为：假设光纤FBG传感器冲击响应信号的采样间隔为t，每组响应信号的采样样本顺序依次为x₁,x₂,…,x_n，按照此顺序将冲击响应信号采样样本一次分为若干个子段，每个子段包含128个采样点；其中第k个子段的128个点构成序列(j＝1,2,…,128；k＝1,2,…)，令

上式中，N^k(Δ)表示采用宽度为Δ的网格覆盖此信号段时，所需的网格数，据此定义瞬时分形量为：

将模糊控制的参数作为此瞬时分形量的函数a^k，根据冲击信号的特征，可以构造若干a^k与函数关系如：

利用上述方法，可以跟据不同函数段k时任意选取一个上述方程计算出相应的模糊控制参数a^k，用此参数对此函数段k的信号进行滤波处理，可以消除大部分杂散波以增加信号纯度。

对瞬态分形计算之后的信号再进行小波包分解，提取第五阶小波包分解的能量总和作为定位的特征信息；最后将提取出的能量总和，根据传感器编号依次记为K_A，K_B，K_C，K_D，K_E，K_F，K_G；

步骤四：基于类二维正态分布模型的光纤FBG传感器冲击响应特征曲面拟合

对于某一个光纤FBG传感器，选取此传感器和相邻传感器连线上的样本点冲击后所得的响应信号，将这些响应信号经第五阶小波包分解后所得能量分别求和；再结合这些样本冲击点的位置坐标，建立一个基于该传感器的包含能量值信息和坐标信息的冲击特征响应集合：

{K_i，p}

其中，i表示上述传感器编号A-G，p表示样本点坐标信息；

根据光纤FBG传感器敏感特性，光纤光栅中心波长偏移量随冲击载荷与传感器之间距离的增大而呈指数衰减趋势；两个相邻光纤FBG传感器连线上样本点的冲击载荷响应信号经瞬态分形计算和小波包分解提取的能量总和随样本点距离增大呈现衰减趋势，与一维正态分布的曲线相契合；

为表示某个光纤FBG传感器在其所在监测子区域内的特性方程，结合该传感器与相邻传感器连线上样本点瞬时载荷响应特性的衰减曲线，可以构造能够表征光纤冲击响应特性的类二维正态分布曲面模型；

标准二维正态分布的曲面模型如下：

其中σ₁,σ₂,μ₁,μ₂,ρ都是常数，称x,y服从参数为σ₁,σ₂,μ₁,μ₂,ρ的二维正态分布，常把这个分布记作N(σ₁,σ₂,μ₁,μ₂,ρ)；

根据上述方程，首先，标准二维正态分布曲面模型在x方向和y方向是没有差异性的，但光纤FBG传感器的敏感特性在垂直于光纤传感器轴向即y方向和平行于光纤传感器轴向即x方向存在明显差异；具体表现为y方向的敏感度要高于x方向上的敏感度，反映在方程上即为变量y包含信息的相关性要高于变量x包含的信息；其次，标准二维正态分布在全空间上的积分等于1，而所需构造的模型在用于光纤FBG传感器敏感特性拟合时则无需此限制；

综合考虑上述两点因素，可以构建适用于表征光纤FBG传感器冲击载荷响应特征的类二维正态分布拟合模型；

光纤FBG传感器冲击载荷平面响应特征的类二维正态分布拟合模型为：

其中，x，y是样本冲击点坐标；z₀，P，m₁，m₂，w₁，w₂是拟合参量；

将冲击特征响应集合{K_i，j}中的元素分别代入上述拟合模型进行类二维正态分布曲面拟合，求得上述拟合参量，可以得到每个光纤FBG传感器在各自待监测子区域中的拟合曲面函数方程：

F_i(i＝A～G)

步骤五：冲击载荷位置辨识

(5-1)如若监测区域内任意一点受到瞬态冲击，且该冲击能量大小与样本冲击能量大小一致，对七个光纤FBG传感器的响应信号依次进行瞬态分形计算和小波包分解第五阶能量和提取，分别选取中心传感器A的响应值K_A和周围六个光纤FBG传感器中最大的响应值K_i。根据如下选取准则，可以确定冲击点加载位置所在待测区域所属子区域：

当K_B为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别该冲击载荷位于Ⅰ区域；

当K_C为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅱ区域；

当K_D为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅲ区域；

当K_E为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅳ区域；

当K_F为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅴ区域；

当K_G为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅵ区域；

(5-2)、由(5-1)可以确定监测子区域及其相应编号的两个光纤FBG传感器，再根据相关两个光纤FBG传感器对应的冲击响应拟合曲面函数F_A，F_i进行联立求解；具体联立方式如下：

Ⅰ：

Ⅱ：

Ⅲ：

Ⅳ：

Ⅴ：

Ⅵ：

其中，x，y是位置坐标；K_i是特征能量值；z_0i，P_i，m_i，n_i，w_1i，w_2i是步骤四拟合所得到的每个光纤FBG传感器在监测区域内的类二维正态分布拟合曲面模型的参量，i为光纤FBG传感器编号；Ⅰ-Ⅵ为划分的子监测区域编号；

由拟合曲面方程可知，所求得x，y有六组解，如果解是实数解，则保持不变，如果解是复数解，则舍去虚部保留其实部；将六组解都转化为实数之后，根据x和y坐标的正负值和所判定的子区域选取合适的解，此解即为冲击载荷的位置坐标。解的选取规则具体如下：

如若初步判别该冲击载荷位于Ⅰ区域，则选取x坐标为负值、y坐标绝对值最小的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅱ区域，则选取x坐标为负值、y坐标为正值且该值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅲ区域，则选取x坐标为正值、y坐标为正值且该值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅳ区域，则选取x坐标为正值、y坐标绝对值最小的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅴ区域，则选取x坐标为正值、y坐标为负值且绝对值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅵ区域，则选取x坐标为负值、y坐标为负值且绝对值较大的那组解作为所确定的冲击载荷位置坐标；

本发明的优点：

首先，在实际大面积区域的冲击监测中，如果能让每个FBG能够检测的区域更大，则FBG的效率就越高。因此利用FBG蜂窝布局在大面积结构冲击监测中提高监测效率。在相同检测面积的情况下，相比于传统正方形布局形式，使用所提出的蜂窝式布局可以减少光纤FBG传感器数量。

其次，基于瞬态分形计算的特征提取方法。瞬态分形计算是一种直接在时域进行的数据计算和滤波方式，其利用信号变化的速度快慢来判断瞬态分量的大小，信号变化的越快，瞬态分量就越高，反之瞬态分量就越低。这样对瞬态分量大小直接进行处理就相当于对信号进行时域变换。采用瞬态分形计算方法可以有效提高光纤FBG传感器冲击响应信号纯净度，有助于消除系统误差，从而为提升特征信号提取的准确性提供依据。

再次，常规基于光纤传感器的结构冲击载荷定位方法，通常需要建立在大量先验知识的基础上。而本方法采用能够表征FBG传感器敏感特性的类二维正态分布曲面进行拟合，只需较少的样本点，即可用拟合得到的类二维正态分布曲面模型，用以表示相关FBG传感器的敏感特性，并通过方程联立求解法获取冲击载荷位置。

附图说明

图1蜂窝结构光纤光栅布局和样本点划分；

图2冲击监测区域划分；

图3类二维正态分布曲面模型例图；

图4冲击载荷定位流程；

具体实施方式

下面结合具体实施例，进一步阐明本发明，应理解这些实施例仅用于本发明而不用于限制本发明的范围，在阅读本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附于权利要求所限定范围。

基于瞬态分形计算和类二维正态分布拟合的冲击载荷定位流程图如图4所示，具体的实施步骤如下：

步骤一：蜂窝结构监测网络布置及相应监测区域划分

将监测区域划分为七个相同的正六边形结构区域，并连接成蜂窝形状，即中间一个正六边形，周围六个正六边形；每个正六边形的正中心横向布置一个光纤FBG传感器，位于中间的光纤传感器记作传感器A，其余的延顺时针方向依次记作传感器B、C、D、E、F、G；

将中间的正六边形视作六个正三角形区，将每个正三角形，以及与其相邻的正六边形合起来作为一个监测区域，整个监测区域分为六个监测子区域，分别为监测子区域Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ；

其中传感器A和传感器B监测子区域Ⅰ；传感器A和传感器C监测子区域Ⅱ；传感器A和传感器D监测子区域Ⅲ；传感器A和传感器E监测子区域Ⅳ；传感器A和传感器F监测子区域Ⅴ；传感器A和传感器G监测子区域Ⅵ；

步骤二：冲击样本点选取规则与冲击响应信号采集

(2-1)、在结构试件的冲击待监测区域上建立一个二维直角坐标系，以光纤光栅传感器A和E连线方向作为x轴正方向，以光纤光栅传感器A和B连线方向作为x轴负方向，以光纤光栅传感器A和传感器C、D中点连线方向作为y轴正方向，以光纤光栅传感器A和传感器F和G中点连线方向作为y轴负方向；冲击样本点选取规则为：在每两个相邻传感器连线上均匀取点，并以这些点作为冲击样本点；

(2-2)、然后利用冲击锤采用相同能量大小对这些冲击样本点依次进行冲击；分别记录每次冲击下，分布式光纤传感网络的冲击响应信号；将每次冲击下的分布式光纤传感网络的冲击响应信号称为一组冲击响应信号；每组冲击响应信号包括七个传感器的相应冲击响应信号，即七个传感器的中心波长偏移量；

步骤三：基于瞬态分形计算的冲击响应特征信息提取

依次对步骤二所得的每一组冲击响应信号进行特征信息提取，即首先采用瞬态分形计算方法对冲击响应信号进行预处理。瞬态分形计算方法是基于分形维数的一种算法，此方法利用瞬时分形量具对时域信号进行处理，可以提高信号纯度；具体体过程为：假设光纤FBG传感器冲击响应信号的采样间隔为t，每组响应信号的采样样本顺序依次为x₁,x₂,…,x_n，按照此顺序将冲击响应信号采样样本一次分为若干个子段，每个子段包含128个采样点；其中第k个子段的128个点构成序列(j＝1,2,…,128；k＝1,2,…)，令

上式中，N^k(Δ)表示采用宽度为Δ的网格覆盖此信号段时，所需的网格数，据此定义瞬时分形量为：

将模糊控制的参数作为此瞬时分形量的函数a^k，根据冲击信号的特征，可以构造若干a^k与函数关系如：

利用上述方法，可以跟据不同函数段k时任意选取一个上述方程计算出相应的模糊控制参数a^k，用此参数对此函数段k的信号进行滤波处理，可以消除大部分杂散波以增加信号纯度。

对瞬态分形计算之后的信号再进行小波包分解，提取第五阶小波包分解的能量总和作为定位的特征信息；最后将提取出的能量总和，根据传感器编号依次记为K_A，K_B，K_C，K_D，K_E，K_F，K_G；

步骤四：基于类二维正态分布模型的光纤FBG传感器冲击响应特征曲面拟合

对于某一个光纤FBG传感器，选取此传感器和相邻传感器连线上的样本点冲击后所得的响应信号，将这些响应信号经第五阶小波包分解后所得能量分别求和；再结合这些样本冲击点的位置坐标，建立一个基于该传感器的包含能量值信息和坐标信息的冲击特征响应集合：

{K_i，p}

其中，i表示上述传感器编号A-G，p表示样本点坐标信息；

根据光纤FBG传感器敏感特性，光纤光栅中心波长偏移量随冲击载荷与传感器之间距离的增大而呈指数衰减趋势；两个相邻光纤FBG传感器连线上样本点的冲击载荷响应信号经瞬态分形计算和小波包分解提取的能量总和随样本点距离增大呈现衰减趋势，与一维正态分布的曲线相契合；

为表示某个光纤FBG传感器在其所在监测子区域内的特性方程，结合该传感器与相邻传感器连线上样本点瞬时载荷响应特性的衰减曲线，可以构造能够表征光纤冲击响应特性的类二维正态分布曲面模型；

标准二维正态分布的曲面模型如下：

其中σ₁,σ₂,μ₁,μ₂,ρ都是常数，称x,y服从参数为σ₁,σ₂,μ₁,μ₂,ρ的二维正态分布，常把这个分布记作N(σ₁,σ₂,μ₁,μ₂,ρ)；

根据上述方程，首先，标准二维正态分布曲面模型在x方向和y方向是没有差异性的，但光纤FBG传感器的敏感特性在垂直于光纤传感器轴向即y方向和平行于光纤传感器轴向即x方向存在明显差异；具体表现为y方向的敏感度要高于x方向上的敏感度，反映在方程上即为变量y包含信息的相关性要高于变量x包含的信息，因此在方程中将y变量的指数幂次数改为三次，用以增加其变量信息权重；其次，标准二维正态分布在全空间上的积分等于1，而所需构造的模型在用于光纤FBG传感器敏感特性拟合时则无需此限制，因此，需要在方程前加上常数变量z₀，用于根据所计算能量值的大小改变模型在坐标轴中的位置；

综合考虑上述两点因素，可以构建适用于表征光纤FBG传感器冲击载荷响应特征的类二维正态分布拟合模型；

光纤FBG传感器冲击载荷平面响应特征的类二维正态分布拟合模型为：

图3所示即为类二维正态分布模型的例图，图中各参数的取值分别为：z₀＝0，P＝1，m₁＝0，m₂＝0，w₁＝0.3，w₂＝0.3。

将冲击特征响应集合{K_i，j}中的元素分别代入上述拟合模型进行类二维正态分布曲面拟合，求得上述拟合参量，可以得到每个光纤FBG传感器在各自待监测子区域中的拟合曲面函数方程：

F_i(i＝A～G)

步骤五：冲击载荷位置辨识

(5-1)如若监测区域内任意一点受到瞬态冲击，且该冲击能量大小与样本冲击能量大小一致，对七个光纤FBG传感器的响应信号依次进行瞬态分形计算和小波包分解第五阶能量和提取，分别选取中心传感器A的响应值K_A和周围六个光纤FBG传感器中最大的响应值K_i。根据如下选取准则，可以确定冲击点加载位置所在待测区域所属子区域：

当K_B为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别该冲击载荷位于Ⅰ区域；

当K_C为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅱ区域；

当K_D为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅲ区域；

当K_E为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅳ区域；

当K_F为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅴ区域；

当K_G为周围六个光纤FBG传感器中响应特征信号最大值时，则初步判别冲击点位于Ⅵ区域；

(5-2)、由(5-1)可以确定监测子区域及其相应编号的两个光纤FBG传感器，再根据相关两个光纤FBG传感器对应的冲击响应拟合曲面函数F_A，F_i进行联立求解；具体联立方式如下：

Ⅰ：

Ⅱ：

Ⅲ：

Ⅳ：

Ⅴ：

Ⅵ：

其中，x，y是位置坐标；K_i是特征能量值；z_0i，P_i，m_i，n_i，w_1i，w_2i是步骤四拟合所得到的每个光纤FBG传感器在监测区域内的类二维正态分布拟合曲面模型的参量，i为光纤FBG传感器编号；Ⅰ-Ⅵ为划分的子监测区域编号；

由拟合曲面方程可知，所求得x，y有六组解，如果解是实数解，则保持不变，如果解是复数解，则舍去虚部保留其实部；将六组解都转化为实数之后，根据x和y坐标的正负值和所判定的子区域选取合适的解，此解即为冲击载荷的位置坐标。解的选取规则具体如下：

如若初步判别该冲击载荷位于Ⅰ区域，则选取x坐标为负值、y坐标绝对值最小的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅱ区域，则选取x坐标为负值、y坐标为正值且该值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅲ区域，则选取x坐标为正值、y坐标为正值且该值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅳ区域，则选取x坐标为正值、y坐标绝对值最小的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅴ区域，则选取x坐标为正值、y坐标为负值且绝对值较大的那组解作为所确定的冲击载荷位置坐标；

如若初步判别该冲击载荷位于Ⅵ区域，则选取x坐标为负值、y坐标为负值且绝对值较大的那组解作为所确定的冲击载荷位置坐标。