具有恒定截面的紧凑型游丝的制作方法
本发明涉及一种紧凑型游丝,更具体地涉及用于与摆轮配合以形成谐振器的这种类型的游丝。
背景技术:
硅制游丝的成本与其表面积基本成比例,即,在相同晶片上能刻蚀的游丝越多,则游丝的单位成本越低。
但是,随意地降低尺寸是不可能的,因为无论在收缩状态或扩展状态,游丝的线圈都必须不能彼此接触。
技术实现要素:
本发明的一个目的是通过提出一种紧凑型游丝来克服全部或部分的上述缺陷,同时保证无论在收缩状态还是扩展状态,游丝的线圈都不会彼此接触。
为此,本发明涉及一种一体式游丝,其包括在内线圈和外线圈之间自身卷绕的单个条带,所述条带在不工作时包括在内线圈的端部和第二线圈之间的第一区域和从第一区域延伸的第二区域,在第一区域中节距(pitch)减小,在第二区域中每一线圈之间的节距连续增加以使得当游丝的收缩角度具有360°的值时,从内线圈到倒数第二线圈在每一线圈之间具有恒定距离。
根据本发明有利地,可以理解的是,游丝尽可能的紧凑且同时保证在收缩状态时以及可能地还在扩展状态时线圈之间的恒定最小距离。因此,可以使游丝的尺寸最小化而不损失计时特性。对于这种游丝,可以优化在相同晶片上刻蚀的游丝的数目以减少单位成本。
根据本发明的其它有利变型:
–在第二区域中,每个线圈之间的节距以恒定的值连续增加;
–第二区域具有恒定的截面;
–在内线圈的端部和内线圈与第二区域的连接点之间,第一区域具有减小的截面;
–第一区域具有与第二区域相同的截面;
–游丝包括从第二区域延伸并且包含在倒数第二线圈的起点和外线圈的端部之间的第三区域,其中节距连续增加以使得当游丝的扩展角度具有360°的值时,在倒数第二线圈和外线圈之间具有最小距离以防止线圈之间的任何接触;
–在第三区域中,节距以恒定的值连续增加;
–第三区域包括第一部分和从第一部分延伸的第二部分,第一部分的截面与第二区域的截面大致相同,第二部分的截面随着它接近外线圈的端部而增加;
–第三区域包括第一部分和从第一部分延伸的第二部分,第一部分的截面与第二区域的截面大致相同,第二部分的截面相对于第二区域的截面增加,并且直到外线圈的端部都是恒定的;
–游丝是硅基的。
另外,本发明涉及一种谐振器,其特征在于,该谐振器包括与根据任一个上述变型的游丝配合的摆轮。
附图说明
从参照附图以非限制性示例的方式给出的下面的描述中,其它特征和优点将清楚地显现,图中:
–图1是在收缩状态的根据本发明的游丝的俯视图;
–图2是在不工作位置的根据本发明的游丝的俯视图;
–图3是在扩展状态的根据本发明的游丝的俯视图;
–图4是示出线圈之间的节距根据游丝的线圈的数目的变化的曲线图;
–图5是示出线圈的厚度根据游丝的线圈的数目的变化的曲线图;
–图6是示出线圈之间的距离根据游丝的线圈的数目和游丝的状态的变化的曲线图;
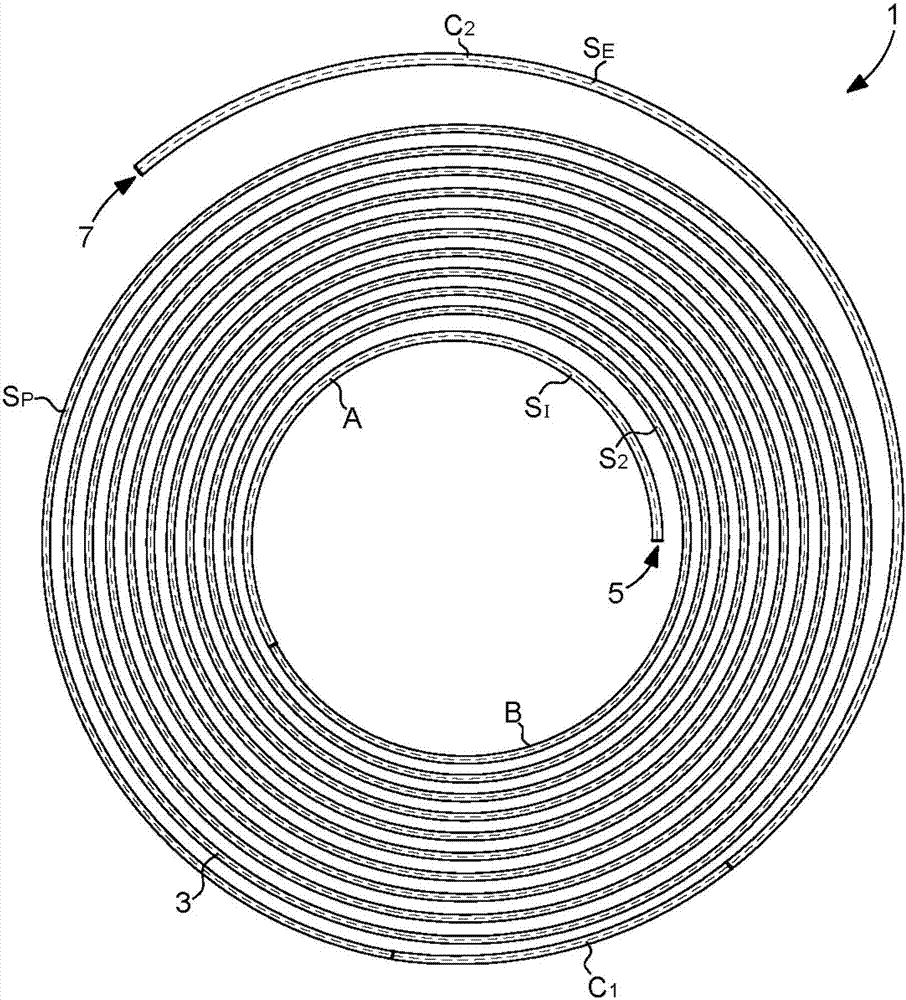
–图7是根据本发明的游丝的一个替代方案的不工作位置的俯视图;
–图8是示出线圈之间的节距根据替代游丝的线圈的数目的变化的曲线图;
-图9是示出线圈的厚度根据替代游丝的线圈的数目的变化的曲线图;
-图10是示出线圈之间的距离根据游丝的线圈的数目和替代游丝的状态的变化的曲线图。
具体实施方式
本发明涉及一种用于与摆轮配合以形成用于钟表的游丝-摆轮型谐振器的紧凑性游丝。当然,游丝可以包括与内线圈的端部成一体的内桩和/或与外线圈的端部成一体的外桩附接部,而不会背离本发明的范围。然而,为了说明书的简单起见,没有示出内桩和/或附接部。
提出本发明的动机是在相同的硅基晶片上制造最大数量的游丝,同时保证每个游丝的线圈无论是在收缩状态还是扩展状态都不彼此接触。但是,可以理解的是,游丝并不限于硅基材料。以非限制性的方式,可以理解的是,相同的逻辑可以应用于以liga方法(即使用导电材料)形成的游丝。
术语“硅基”是指包括单晶硅、掺杂单晶硅、多晶硅、掺杂多晶硅、多孔硅、氧化硅、石英、硅土、氮化硅或碳化硅的材料。当然,当硅基材料处于结晶相时,可以使用任何结晶取向。
如在图2中示出的,本发明因而涉及一种一体式游丝1,其包括在内线圈si和外线圈se之间自身卷绕的单个条带3。根据本发明,在图2中以不工作位置示出的游丝1的条带3包括在内线圈si的端部5和第二线圈s2的起点之间的第一区域a,其中内线圈si和第二线圈s2之间的节距减小。
有利地,游丝1包括从第一区域a延伸的第二区域b,其中每个线圈之间的节距连续增加,使得当游丝1在其收缩状态时,即,当内线圈si的端部5已完成相对于游丝1的中心的大致-360°的转动时,如图1中所示的,从内线圈si到倒数第二线圈sp在每一线圈之间具有大致恒定的距离。
优选地,如在图4中示出的,在第二区域b中每一线圈之间的节距以大致恒定的值连续增加。另外,根据本发明优选地,第二区域b具有恒定的截面。因此,例如,所述恒定截面可以具有在10μm和50μm之间的恒定厚度,以及在50μm和250μm之间的恒定高度。
根据另外的一个可选特征,有利地根据本发明,游丝包括从第二区域b延伸并且包含在倒数第二线圈sp的起点和外线圈se的端部7之间的第三区域c,其中在倒数第二线圈sp和外线圈se之间,节距连续增加,以使得当游丝1在扩展状态时,即,当内线圈si的端部5已相对于游丝1的中心完成大致+360°旋转时,如在图3中看到的,在倒数第二线圈sp和外线圈se之间存在最小距离以阻止接触,特别是在倒数第二线圈sp和外线圈se之间的接触。
优选地,如在图4中示出的,在第三区域c中每一线圈之间的节距以第二大致恒定值连续增加。如在图4中看到的,第二大致恒定值优选地大于第二区域b的第一大致恒定值。另外,根据本发明优选地,第三区域c包括具有与第二区域b的厚度大致相同的厚度的第一部分c1,以及之后的厚度连续增加的第二部分c2。
在图4中示出了第一曲线图,其示出线圈之间的节距p根据游丝的线圈的数目的变化。可以看到在游丝1的第一区域a中,节距以大致恒定的方式减小,直到第二区域b的起点。在图4中可以看到,第二区域b的节距基本恒定地增加,直到第三区域c。该第三区域c的节距基本恒定地增加,直到外线圈se的端部7。如在图4中看到的,第三区域c中的基本恒定的节距增加比区域b中的基本恒定的节距增加更为显著得多。
以补充的方式,在图5中示出了第二曲线图,其示出线圈的厚度e根据游丝的线圈的数目的变化。可以看出,在游丝1的第一区域a中厚度减小,直到第二区域b的起点。在图5中,可以看到第二区域b具有恒定的厚度,直到第三区域c。区域c具有厚度保持恒定的第一部分c1和从第一部分c1延伸的第二部分c2,该第二部分c2的厚度朝向外线圈se的端部7增加。
最后,示出了线圈之间的距离△p根据游丝的线圈的数目的变化的曲线图在图6中示出。更为具体地,针对处于图1中的收缩状态的游丝(用方块□标记的曲线)、处于图2中的不工作状态的游丝(用三角△标记的曲线)以及处于图3中的扩展状态的游丝(用圈o标记的曲线),示出了线圈之间的距离△p。
因此,在使用圈(o)标记的扩展状态下,可以看到,在游丝1的第一区域a中,线圈之间的距离△p减小,直到第二区域b的起点。要注意的是,之后,在第二区域b和第三区域c中,线圈之间的距离△p连续增加,直到与端部7的外桩的固定附接点使线圈之间的距离回到最小值。
这是符合逻辑的,因为在其不工作状态下,在图6中使用三角(△)标记的曲线与图4的曲线相同。最后,在使用方块(□)标记的收缩状态下,可以看出,在游丝1的第一区域a和第二区域b中,线圈之间的距离△p大致恒定并且等于最小值。然后应注意的是,在第三区域c中,朝向外线圈se的端部7,线圈之间的距离△p连续增加。
在图6中,应注意的是,具有圈(o)和方块(□)的曲线的最小值不相同。然而,可以使它们在几何上相同。
类似地,在图4至6中描述的值仅仅用作示例。取决于游丝的构型和/或其所属于的谐振器的构型,所选择的最小值可以不同于图6中作为示例选择的20μm。因而清楚的是,具有圈(o)和方块(□)的曲线的最小值可以均选择为小于或大于20μm。
然而可以理解的是,根据本发明有利地,游丝1的这些特别的特征赋予游丝在不工作状态时的最大紧凑度,同时保证了在压缩状态以及可能地在扩展状态中的线圈之间的恒定最小距离。典型地,在不工作状态的游丝1具有最大半径为大约1.2毫米(即,游丝1的几何中心与外线圈se的端部7之间的距离)的11.4个线圈。为了完整性起见,研究显示游丝1的几何中心与内线圈se的端部5之间的距离为大约0.5毫米。因此,游丝的尺寸可以最小化,而不会由此损失计时特性。对于本发明的游丝,可以优化在相同晶片上刻蚀的游丝的数目,以减少单位成本。
当然,本发明不限于所示出的实施例,而可以有本领域技术人员想到的各种变型和修改。特别地,几何特征,即节距和截面的变化,例如线圈的厚度和数量,根据所设想的应用可以变化。
作为示例,在图7中示出图2的一个替代方案。本发明的该替代方案因而涉及一种一体式游丝11,其包括在内线圈si和外线圈se之间自身卷绕的单个条带13。根据本发明,处于图7所示的不工作位置的游丝11的条带13包括在内线圈si的端部15和第二线圈s2的起点之间的第一区域a,在该第一区域a中内线圈si和第二线圈s2之间的节距减小。
有利地,游丝11包括从第一区域a延伸的第二区域b,其中每个线圈之间的节距连续增加,使得当游丝11收缩时,即,当内线圈si的端部15已完成相对于游丝11的中心的大致-360°的转动时(如同游丝1),从内线圈si到倒数第二线圈sp在每一线圈之间具有大致恒定的距离。
优选地,如在图8中示出的,在第二区域b中每一线圈之间的节距以大致恒定的值连续增加。另外,根据该替代方案优选地,第二区域b具有恒定的截面。因此,例如,所述恒定截面可以具有在10μm和50μm之间的恒定厚度,以及在50μm和250μm之间的恒定高度。
根据另外的一个可选特征,有利地根据本发明,游丝11包括从第二区域b延伸并且包含在倒数第二线圈sp的起点和外线圈se的端部17之间的第三区域c,其中在倒数第二线圈sp和外线圈se之间节距连续增加,以使得当游丝11扩展时,即,当内线圈si的端部15已相对于游丝11的中心完成大致+360°旋转时(如同游丝1),在倒数第二线圈sp和外线圈se之间存在最小距离以防止接触,特别是在倒数第二线圈sp和外线圈se之间的接触。
优选地,如在图8中示出的,在第三区域c中每一线圈之间的节距以第二大致恒定值连续增加。如在图8中看到的,第二大致恒定值优选地大于第二区域b的第一大致恒定值。另外,根据本发明优选地,第三区域c包括具有与第二区域b的厚度大致相同厚度的第一部分c1,以及之后的第二部分c2,在第二部分c2中厚度相对于区域b增加并且保持恒定直到外线圈se的端部17。
在图8中示出了第一曲线图,其示出线圈之间的节距p根据游丝11的线圈的数目的变化。可以看到,在游丝11的第一区域a中节距减小,直到第二区域b的起点。在图8中可以看到,第二区域b具有大致恒定的节距增加,直到第三区域c。区域c具有大致恒定的节距增加,直到外线圈se的端部17。如在图8中看到的,在第三区域c中的大致恒定的节距增加比在区域b中的更为显著得多。
以补充的方式,在图9中示出了第二曲线图,其示出线圈的厚度e根据游丝11的线圈的数目的变化。可以看出,在第一区域a和第二区域b中,游丝11具有恒定的厚度,直到第三区域c。区域c包括其截面与第一区域a和第二区域b的截面大致相同的第一部分c1和从第一部分c1延伸的第二部分c2,该第二部分c2的截面相对于第二区域b的截面增加,并且直到外线圈se的端部17都是恒定的。
最后,示出了线圈之间的距离△p根据游丝11的线圈的数目的变化的曲线图在图10中示出。更为具体地,针对处于其收缩状态的游丝11(用方块□标记的曲线)、处于图7中的不工作状态的游丝11(用三角△标记的曲线)以及处于其扩展状态的游丝11(用圈o标记的曲线),示出了线圈之间的距离△p。
因此,在使用圈(o)标记的扩展状态下,可以看到,在游丝11的第一区域a中,线圈之间的距离△p减小,直到第二区域b的起点。要注意的是,之后,在第二区域b和第三区域c中,线圈之间的距离△p连续增加,直到与端部17的外桩的固定附接点使线圈之间的距离回到最小值。
这是符合逻辑的,因为在其不工作状态下,在图10中使用三角(△)标记的曲线与图8的曲线相同。最后,在使用方块(□)标记的收缩状态下,可以看出,在游丝11的第一区域a中,线圈之间的距离△p减小,直到第二区域b的起点。然后,在游丝11的第二区域b中,线圈之间的距离△p有利地恒定并且等于最小值。然后应注意的是,在第三区域c中,中,朝向外线圈se的端部17,线圈之间的距离△p连续增加。
在图10中,应注意的是,具有圈(o)和方块(□)的曲线的最小值不相同。然而,可以使它们在几何上相同。
类似地,在图8至10中描述的值仅仅用作示例。取决于游丝的构型和/或其所属于的谐振器的构型,所选择的最小值可以不同于图10中作为示例选择的20μm。因而清楚的是,具有圈(o)和方块(□)的曲线的最小值可以均选择为小于或大于20μm。
然而可以理解的是,根据本发明有利地,游丝11的这些特别的特征赋予游丝在不工作状态时的最大紧凑度,同时保证了在压缩状态以及可能地在扩展状态中的线圈之间的基本恒定的最小距离。典型地,在不工作状态的游丝11具有最大半径为大约1.6毫米(即,游丝11的几何中心与外线圈se的端部17之间的距离)的11.6个线圈。为了完整性起见,研究显示游丝11的几何中心与内线圈se的端部15之间的距离为大约0.5毫米。因此,游丝的尺寸可以最小化,而不会由此损失计时特性。对于本发明的游丝,可以优化在相同晶片上刻蚀的游丝的数目,以减少单位成本。
另外,线圈的数量可以减少,以便进一步减小游丝1、11的尺寸。
还清楚的是,360°的收缩或扩展角度可以更小而不会背离本发明的范围。事实上,该角度的选择是因为从机械方面该角度在理论上不能被超过。但是,重点不是在哪个角度距离最小,而是保证最小距离决不被超过。因此可以理解的是,该角度可以有意地选择为更小,因为根据机芯的构型清楚的是,该角度在常规操作中将不会被超过。
另外,在图4中的纵坐标值是非限制性的。因此,取决于第二区域b的截面,第一区域a和/或第三区域c的最大节距可以变化。因而清楚的是,仅保留节距的变化,而不必具有相同的最小和/或最大值。
类似地,在图5中的纵坐标值是非限制性的。因此,取决于第二区域b的厚度,第一区域a和/或第三区域c的最大厚度可以变化。因而可以理解的是,仅保留厚度的变化,而不必具有相同的最小和/或最大值。
还可以结合图2和图7的示例,而不会背离本发明的范围。作为示例,因而可以设想提出一种具有图2的区域a和b以及图7的区域c的游丝,或者具有图2的区域b和c以及图7的区域a的游丝。
最后,尽管基于厚度的变化进行估算,但是清楚的是,该变化必须理解为截面的变化,即,游丝的条带的高度和/或厚度的变化。
- 还没有人留言评论。精彩留言会获得点赞!