适用双线性对密码芯片的协处理器实现方法与流程

本发明涉及密码学领域，特别是涉及一种适用双线性对密码芯片的协处理器实现方法。

背景技术：

在现实生活中，应用需求往往对密码芯片提出了很高的要求，比如要求在几毫秒内完成整个密码运算。为了达到这个要求，研究人员在密码芯片中设计了专用的硬件来加速密码的运算速度，这种专用硬件通常称为协处理器。

双线性对广泛应用于三方密钥协商、短签名、基于身份的密码等众多领域。双线性对是一个映射，它把椭圆曲线E(GF(p))上的两个点映射到有限域GF(p^k)中的一个元素。在安全级别为128比特时，目前普遍认为BN曲线是一类理想的曲线，用于实现双线性对。BN曲线定义为：E(GF(p))：y²＝x³+b，其中b≠0，而且素数p可以表示成多项式形式p(t)＝36t⁴+36t³+24t²+6t+1，嵌入次数k＝12。在计算BN曲线上的双线性对时，需要在有限扩域GF(p¹²)中运算。由于GF(p¹²)的运算相对比较复杂，研究人员把它们化简成GF(p²)中的运算。

复旦大学的韩军教授在2015年针对GF(p²)设计了一个模乘。其思想是 把GF(p²)表示成GF(p)[x]/(i²+1)，于是GF(p²)中的元素A，B可以表示成A＝a₀+a₁i，B＝b₀+b₁i。这样GF(p²)中的模乘

A*B mod p≡(a₀+a₁i)(b₀+b₁i)≡(a₀b₀+(-a₁)b₁)+(a₀b₁+

a₁b₀)i mod p＝[ψ(a₀，b₀，-a₁，b₁)+ψ(a₀，b₁，a₁，b₀)i]mod p

这里ψ是一个函数，满足ψ(a，b，c，d)＝(a·b+c·d)mod p。韩军教授给出了如下计算(a·b+c·d)·2^-rnmod p的算法，并实现在协处理器中。

输入：0≤A，B，C，D≤-2p，β²*p≤2^r(n-1），P₁′＝(1+P₁)2^-r，P₂′＝(1+P₂)2^-r，

其中P₁＝((-p)mod 2^r)p，P₂＝((-p)mod 2^2r)p，a_i，c_i∈(0，1，…，2^r-1}

输出：(AB+CD)R^-1≤4*2^rp，其中R^-1＝2^-rn。

步骤1.S₀＝0，Q_-1＝0；

步骤2.从i＝0到n循环；

步骤2.1.Q_i＝S_i mod 2^r；

步骤2.2.S_i+1＝(S_i＞＞r)+Q_i-1P₂′+a_i B+c_i D；

步骤3.S_n+2＝S_n+1+Q_nP₁′；

步骤4.输出S_n+2。

以上算法的计算速度与原来的蒙哥马利模乘差不多，但它在芯片上实现时，面积会更小。

技术实现要素：

本发明要解决的技术问题是提供一种适用双线性对密码芯片的协处理器实现方法，能够加快双线性对的运算，提高运算速度，计算效率更高。

为解决上述技术问题，本发明的适用双线性对密码芯片的协处理器实现方法，包括如下步骤：

输入：s＝2⁹+2⁸+2⁶+2⁴+2³+1，p(t)＝36t⁴+36t³+24t²+6t+1；

输出：(a(t)·b(t)+c(t)·d(t))·t^-5mod p(t)；

步骤1.S＝0；

步骤2.从i＝0到4循环；

步骤2.1.q＝-(S₀+a_i·b₀+c_i·d₀)；

步骤2.2.S＝(S+a_i·b(t)+c_i·d(t)+q·p(t))/t；

步骤3.从i＝0到3循环；

步骤3.1.μ＝S_i div 2^m，Y＝S_i mod 2^m-s·μ；

步骤3.2.S_i+1＝S_i+1+μ，S_i＝γ；

步骤4.输出S。

由于p(t)＝36t⁴+36t³+24t²+6t+1，所以q·p(t)可以通过移位来实现，因为36·q＝2⁵·q+2²·q。而移位运算相对于乘法来说，是非常快的。

在本发明的方法中，由于协处理器利用素数p的特殊形式，把蒙哥马利模乘结合多项式运算，加快了双线性对的运算，相比现有的同类型协处理器，具有更快的速度。

采用本发明的方法能够加快双线性对的运算，提高运算速度，计算效率更高。

附图说明

下面结合附图与具体实施方式对本发明作进一步详细的说明：

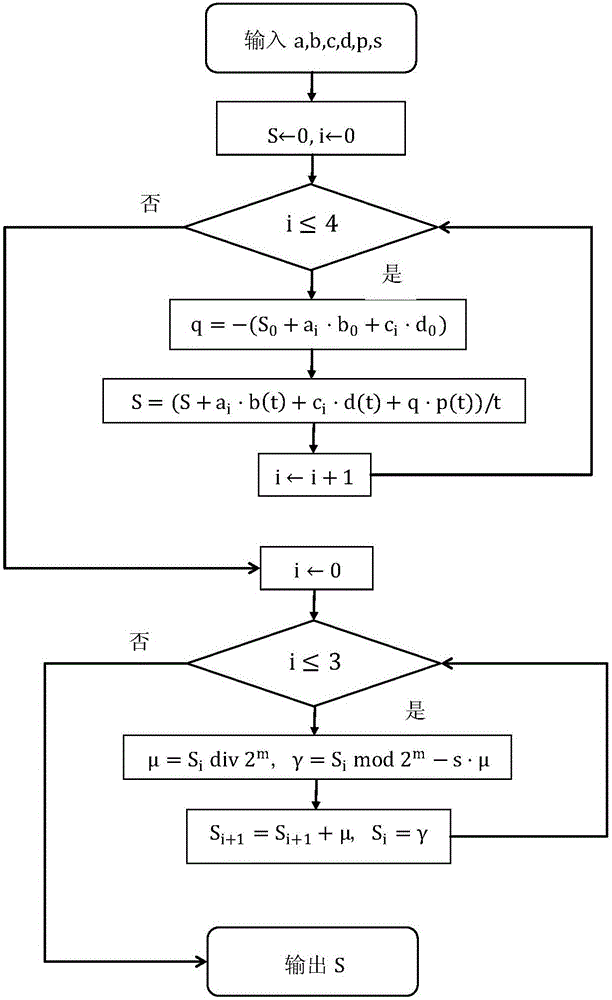
附图是所述适用双线性对密码芯片的协处理器实现方法流程图。

具体实施方式

事实上，BN曲线的素数p具有特殊的形式：p(t)＝36t⁴+36t³+24t²+6t+1。利用这种特殊形式，所述适用双线性对密码芯片的协处理器实现方法设计了一个计算 (a(t)·b(t)+c(t)·d(t))·t^-5 mod p(t)的协处理器，它比现有的协处理器效率更高。

首先，令于是

即存在一个整数q_i使得t·S[i+1]＝S[i]+a_i·B+c_i·D+q_i·p(t)。这就意味着S[i]+a_i·B+c_i·D+q_i·p(t)≡0mod t。从而q_i＝-(S[i]+a_i·B+c_i·D)·p(t)^-1mod t。由于p(t)＝36t⁴+36t³+24t²+6t+1，所以p(t)^-1mod t＝1，因此q_i＝-(S[i]+a_i·B+c_i·D)mod t＝-(S[i]₀+a_i·b₀+c_i·d₀)。再借鉴多项式的蒙哥马利模乘就可以得到如下算法：

以下通过实例来说明：使用本发明的协处理器计算(a·b+c·d)mod p。

取t＝2⁶³+2⁹+2⁸+2⁶+2⁴+2³+1。随机生成256比特的四个整数：

a＝102348664359136354121555995703331209944670783887711539539355540773580750896789：

b＝15198594237847085601921741643113035313376060617059415121829173576864961682539：

c＝37537999104488012760437156306276567607184363706308116220282999703143332077143：

d＝49777162161443782885518318738983329512955140678191822655100949720665351977521。

把它们分别表示成多项式形式：

a＝14·t⁴+1313454928633441003·t³+6716857382264123731·t²+6776786016679099608·t+9107082293041855369：

b＝2·t⁴+923461959009233704·t³+147983662995381657·t²+7190738846814756917·t+8029590559694131659：

c＝5·t⁴+1724326002491775644·t³+5890993479525028433·t²+4099338599590126099·t+9072044628884367258：

d＝6·t⁴+8099443297690894381·t³+702227503073076349·t²+1929651357207594006·t+851144369974360131。

在步骤2中，

当i＝0时，q＝-80847761716597529940296817162079017969；

S＝-2910519421797511077778038985475454732598·t³

-2828630866676550176286264610948463912810·t²

-1932627942553907022232297042767957083781·t

-402094036643095713681447907950204314893

当i＝1时，q＝344190090648842303583911263653548866252；

S＝12390843263358322929058955095158658140882·t³

+9519784306196976537861479207420951790225·t²

+5435812830822790420233005513146552500245·t

+189152994098184802613413495874222664861

当i＝2时，q＝-248100694659278041850019341183559569313；

S＝-8931625007734009506551916606966466077208·t³

+3513134785555404436066092247642090010211·t²

+3570498437175295183610916335959542760097·t

+4006875393737349838857180341612641554292

当i＝3时，q＝-4018889549401909915473063230774843017633；

S＝-144680023778468756957017303442022131098918·t³

-153596469779857384148223065849605939290520·t²

-92938809161075701242251612225918373887254·t

-20530066799846322920828978526140818488086

当i＝4时，q＝20530066799846322920712308536455228844205；

S＝7390824047944671525145643107312388238391438·t³

+594402381015998868188679229554280691036223·t²

+339125133416454365948877921934116853695343·t

+30241591638002236282132557593454443744844

在步骤3中

当i＝0时，

S＝739082404794467625145643107312388238391438·t³

+594402381015998868188679229554280691036223·t²

+339125133416454365952156721869451002610306·t

-2809924058051358997993551

当i＝1时，

S＝739082404794467625145643107312388238391438·t³

+594402381015998868225447250193736327042349·t²

-31510185607183855299239484·t-2809924058051358997993551当i＝2时，

S＝7390824104794467625210088342595198491516180·t³

-55229560612314748468703081·t²-31510185607183855299239484

·t-2809924058051358997993551

当i＝3时，

S＝80131474892397279746106·t⁴-68672669498333066041900310·t³

-55229560612314748468703081·t²-31510185607183855299239484

·t-2809924058051358997993551

最后输出

S＝

80131474892397279746106·t⁴-68672669498333066041900310·t³-

55229560612314748468703081·t²-31510185607183855299239484·t-

2809924058051358997993551

把t＝2⁶³+2⁹+2⁸+2⁶+2⁴+2³+1代入S并计算S·t⁵mod p，

就可得到

(a·b+c·d)mod p

＝2327170183370832094786358000118527218072270768159483545375521057608

35137881787

以上通过实施例，对本发明进行了详细的说明，但本发明的保护范围不限于所述的实施例。在不脱离本发明原理的情况下，本领域技术人员还可做出许多变形和改进，这些也应视为本发明的保护范围。