模拟三维地下水流运动的三重网格多尺度有限元方法与流程

本发明属于水力学
技术领域：
，具体涉及一种模拟三维地下水流运动的三重网格多尺度有限元方法。
背景技术：
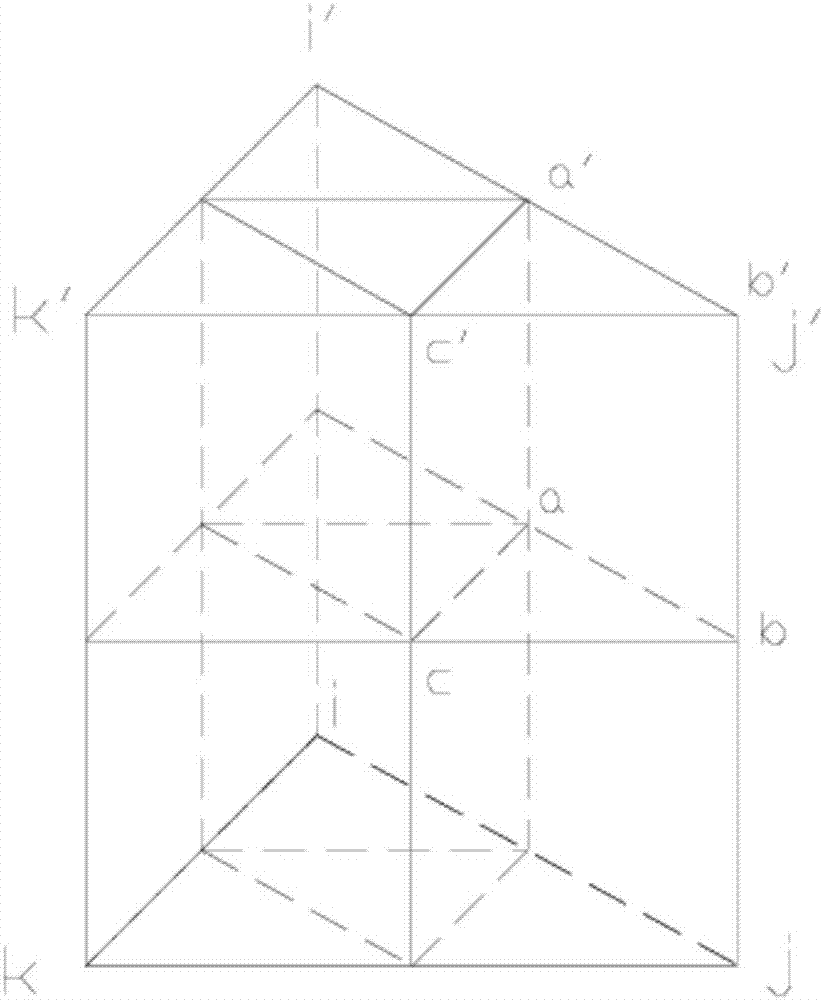
：随着经济、科技的快速发展，人们对于地下水数值模拟越来越关注，所研究的地下水问题也越来越复杂，如地面沉降、海水入侵、流域水资源评估等。因此，研究地下水的分布、运动的高效数值方法能够帮助我们对地下水系统有更好的了解越认识，具有重要的研究价值。由于地下水问题具有非均质性，并且其非均质性常跨越了很多尺度。如果运用传统有限单元法直接求解介质所有尺度，需要精细剖分保证单元内部渗透系数可视为常数，以保证精度，需要大量计算消耗，计算效率很低。为了解决这一难点问题，科学工作者提出了多尺度有限单元法(houandwu1997)用于地下水数值模拟，该方法通过构造多尺度基函数抓住介质信息，可以直接在粗尺度单元上求解，从而大幅降低所需的计算消耗并保证精度(houandwu1997,yeetal.2004)。许多实际和数值模拟工作也证明了多尺度有限单元法具有和精细剖分的有限单元法相同的精度，并具有更高的计算效率。近年来，更加复杂的大尺度地下水问题备受关注，研究区的空间尺度和时间尺度也越来越大，需要大量的计算消耗进行求解。在求解此类问题时，多尺度有限单元法效率较低的基函数构造算法降低了整体计算效率，限制了它的发展空间。同时，多尺度有限单元法缺乏成熟的达西速度算法，在精确描述水流速度方面存在一定困难。针对上述问题，本发明将采用区域分解算法提高多尺度有限单元法三维基函数的构造效率，降低构造消耗。在三维连续达西速度求解方面，本发明将借鉴yeh在1981年于“onthecomputationofdarcianvelocityandmassbalanceinthefiniteelementmodelingofgroundwaterflow”一文中提出有限元模型。区域分解法和yeh的有限元模型在以往的研究中均展现了良好的稳定性及有效性，因此本发明的工作具有极强的可行性。技术实现要素：本发明的目的在于提供一种模拟三维地下水流运动的三重网格多尺度有限元方法，以解决现有技术中求解三维大尺度地下水问题时三维多尺度基函数构造效率较低的问题，该方法集合区域分解技术，通过将构造问题分解子问题降低所需的计算消耗；在此基础上，本发明还将结合yeh的有限元模型，实现三维连续达西速度场的高效计算。为达到上述目的，本发明的一种模拟三维地下水流运动的三重网格多尺度有限元方法，包括步骤如下：(1)根据研究区域确定所要模拟的三维地下水头问题的边界条件，设定粗尺度，剖分该研究区域，得到粗单元；(2)设定中尺度，剖分上述粗单元，得到中单元；(3)设定细尺度，剖分上述中单元，得到细单元；(4)运用细单元顶底面的二维有限元线性基函数和插值函数，在每个细单元、中单元上构造改进的三维线性基函数；(5)在步骤(2)中的网格剖分下，根据渗透系数k、粗单元顶点上的三维多尺度基函数值以及三维多尺度基函数边界条件公式，在粗单元的各个面和棱上求解退化的椭圆型问题，获得三维多尺度基函数在粗单元所有边界节点上的值；(6)根据渗透系数k、粗单元所有边界节点上的三维多尺度基函数值以及改进的三维线性基函数，以中单元为最小子单元，在粗单元上求解退化的椭圆型问题，确定所有中单元顶点上的三维多尺度基函数值；(7)在粗单元上以细单元为最小子单元考虑退化的椭圆型问题，运用区域分解技术将该椭圆型问题分解为每个中单元上的子问题；(8)根据渗透系数k、中单元顶点上的三维多尺度基函数值以及三维多尺度基函数边界条件公式，在中单元的各个面和棱上求解退化的椭圆型问题，获得三维多尺度基函数在中单元所有边界节点上的值；(9)根据渗透系数k、中单元所有边界节点上的三维多尺度基函数值以及改进的三维线性基函数，以细单元为最小子单元，在每个中单元上求解子问题，得到三维多尺度基函数在每个中单元中所有节点上的值，从而获得三维多尺度基函数在粗单元上所有节点上的值，完成三维多尺度基函数的构造；(10)计算每个粗单元上的单元刚度矩阵，相加得总刚度矩阵；根据研究区域的边界条件、源汇项，计算右端项，形成有限元方程；(11)采用choleshy分解法，求得研究区域上每个节点的水头；(12)根据所要模拟的研究区域确定三维地下水速度问题的边界条件，在研究区上对达西方程进行变分，并使用上述步骤(1)-(3)中所获的三重网格对研究区剖分；(13)根据yeh的有限元模型理论，运用上述步骤(9)中获得的三维多尺度基函数在研究区上直接求解达西方程，结合上述的改进的三维线性基函数及渗透系数k，以细单元为最小子单元，获得每一粗单元上的关于速度的单元刚度矩阵，相加得总刚度矩阵；根据研究区域的边界条件计算右端项，形成有限元方程；(14)采用choleshy分解法，求得研究区域上每个节点的达西速度。优选地，上述的步骤(1)中，采用三棱柱单元剖分研究区域，以形成粗单元。优选地，上述的步骤(2)中，采用三棱柱单元剖分粗单元，以形成中单元。优选地，上述的步骤(3)中，采用三棱柱单元剖分中单元，以形成细单元。优选地，上述的步骤(6)中，所述的研究区域最小子单元上的渗透系数k取这个单元的所有顶点上的渗透系数平均值。优选地，上述的步骤(9)中，所述的研究区域最小子单元上的渗透系数k取这个单元的所有顶点上的渗透系数平均值。优选地，上述的步骤(13)中，所述的研究区域最小子单元上的渗透系数k取这个单元的所有顶点上的渗透系数平均值。优选地，上述的步骤(10)中，细单元上的源汇项值取这个单元的所有顶点上的源汇项的平均值。优选地，上述的步骤(10)中，粗单元上的源汇项值取这个单元中所有细单元的源汇项的平均值。本发明的有益效果：1.将多尺度有限单元法的三维粗单元剖分为中、细两重单元，可以根据渗透系数的变化灵活调整粗单元的剖分；2.构造了一种改进的三维线性基函数，比传统三维线性基函数更加简单，构造时所需计算量更少；3.将三维多尺度基函数的构造问题转化为多个子问题，降低了每次所需求解的矩阵的阶数，节约了大量计算消耗；4.在研究区剖分相同时，本发明模拟地下水流问题的水头精度与多尺度有限单元法、精细剖分的有限单元法相近，但计算时间远少于这两种方法；5.在研究区剖分相同时，本发明模拟地下水流达西速度的精度与精细剖分的yeh的有限元方法相近，可以节约大量的计算消耗；能保证达西速度的连续性；6.本发明能够高效求解稳定流和非稳定流问题，可以有效处理连续、突变、随机对数正态分布变化的非均质介质。附图说明图1a为传统多尺度有限单元法的三维粗单元剖分示意图。图1b为本发明的粗单元剖分为中单元的示意图。图1c为本发明的中单元剖分为细单元的示意图。图2为三维连续介质稳定流模型，子例1.1中各数值方法在y＝4050m，z＝5m平面处的水头场的示意图。图3为三维连续介质稳定流模型，子例1.1中各数值方法在y＝4050m，z＝5m平面处的粗尺度达西速度场的示意图。图4为三维连续介质稳定流模型，子例1.2中各数值方法在y＝4050m，z＝5m处的水头相对误差的示意图。图5为三维随机对数正态分布介质稳定流模型，各数值方法在y＝520m，z＝60m处的水头值的示意图。图6三维水平渐变垂向突变介质非稳定流模型，各数值方法在y＝5000m，z＝60m处的水头值的示意图。具体实施方式为了便于本领域技术人员的理解，下面结合实施例与附图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。本发明的一种模拟三维地下水流运动的三重网格多尺度有限元方法，包括步骤如下：(1)根据研究区域确定所要模拟的三维地下水头问题的边界条件，设定粗尺度，剖分该研究区域，得到粗单元；(2)设定中尺度，剖分上述粗单元，得到中单元；(3)设定细尺度，剖分上述中单元，得到细单元；(4)运用细单元顶底面的二维有限元线性基函数和插值函数，在每个细单元、中单元上构造改进的三维线性基函数；(5)在步骤(2)中的网格剖分下，根据渗透系数k、粗单元顶点上的三维多尺度基函数值以及三维多尺度基函数边界条件公式，在粗单元的各个面和棱上求解退化的椭圆型问题，获得三维多尺度基函数在粗单元所有边界节点上的值；(6)根据渗透系数k、粗单元所有边界节点上的三维多尺度基函数值以及改进的三维线性基函数，以中单元为最小子单元，在粗单元上求解退化的椭圆型问题，确定所有中单元顶点上的三维多尺度基函数值；(7)在粗单元上以细单元为最小子单元考虑退化的椭圆型问题，运用区域分解技术将该椭圆型问题分解为每个中单元上的子问题；(8)根据渗透系数k、中单元顶点上的三维多尺度基函数值以及三维多尺度基函数边界条件公式，在中单元的各个面和棱上求解退化的椭圆型问题，获得三维多尺度基函数在中单元所有边界节点上的值；(9)根据渗透系数k、中单元所有边界节点上的三维多尺度基函数值以及改进的三维线性基函数，以细单元为最小子单元，在每个中单元上求解子问题，得到三维多尺度基函数在每个中单元中所有节点上的值，从而获得三维多尺度基函数在粗单元上所有节点上的值，完成三维多尺度基函数的构造；(10)计算每个粗单元上的单元刚度矩阵，相加得总刚度矩阵；根据研究区域的边界条件、源汇项，计算右端项，形成有限元方程；(11)采用choleshy分解法，求得研究区域上每个节点的水头；(12)根据所要模拟的研究区域确定三维地下水速度问题的边界条件，在研究区上对达西方程进行变分，并使用上述步骤(1)-(3)中所获的三重网格对研究区剖分；(13)根据yeh的有限元模型理论，运用上述步骤(9)中获得的三维多尺度基函数在研究区上直接求解达西方程，结合上述的改进的三维线性基函数及渗透系数k，以细单元为最小子单元，获得每一粗单元上的关于速度的单元刚度矩阵，相加得总刚度矩阵；根据研究区域的边界条件计算右端项，形成有限元方程；(14)采用choleshy分解法，求得研究区域上每个节点的达西速度。设△123-456为属于粗单元△ijk-i’j’k’的三棱柱细单元(或中单元)，其中三角形△123和△456分别为△123-456底面和顶面，高度分别为和在三角形△123和△456上，水头可以由有限元二维线性基函数表示：为了构造改进的三维线性基函数，本发明构造了如下插值函数来描述基函数垂直方向的变化：根据有限元理论，在△123-456上，水头可以表示为：展开得：其中，为本发明的改进的三维线性基函数。在粗单元中的棱(包括中单元的棱)ξη上，三维多尺度基函数ψi的边界条件通项公式如下：线性：振荡：在粗、中单元的各个边界面上，需要通过求解二维的退化椭圆型问题，获得三维多尺度基函数在各个面上节点的值。和传统多尺度有限单元法的粗单元剖分方式(图1a)不同，三重网格多尺度有限单元法的粗单元需要先被剖分为中单元(图1b)再将每个中单元剖分为细单元(图1c)。该方法的三维多尺度基函数的具体构造过程如下：在三棱柱粗单元△ijk-i’j’k’上考虑三维的退化的椭圆型方程：▽·k▽ψi＝0,其中ψi为与i点相关的三维多尺度基函数，k为渗透系数，三维多尺度基函数的具体构造过程分为三个过程：过程一：在上述步骤(2)(图1b)的剖分网格下，以中单元为最小子单元，求解退化的椭圆型方程，得到图1b中所有节点上的三维多尺度基函数的值；过程二：运用区域分解技术将粗单元上的三维多尺度基函数构造问题转换为中单元上的子问题；过程三：在每个中单元上(图1c)，以细单元为最小单元，求解退化的椭圆型方程即可得到三维多尺度基函数在所有中单元上所有节点的值，从而获得粗单元上所有节点的值。完成上述三维多尺度基函数的求解之后，即可以得到粗单元上的单元刚度矩阵，相加得总刚度矩阵，再运用cholesky分解法或者其他矩阵求解算法求解总刚度矩阵和右端项的方程组即可获得水头值。获得研究区所有节点的水头值之后，根据yeh的有限元模型(yeh1981)的原理，运用上述过程中构造的三维多尺度基函数在研究区上直接求解达西方程，结合所构造的改进的三维线性基函数获得每一粗单元上的关于速度的单元刚度矩阵，相加得总刚度矩阵；根据研究区域的边界条件计算右端项，形成有限元方程；再运用cholesky分解法或者其他矩阵求解算法求解总刚度矩阵和右端项的方程组即可获得速度值。下面结合具体实施例对本发明做进一步的解释，其中涉及一些简写符号，以下为注解：as:解析解fem:有限单元法(精细剖分)；method-yeh:yeh的有限单元模型(精细剖分)；msfem:多尺度有限单元法，应用基函数的振荡边界条件；etmsfem:三重网格多尺度有限单元法，应用基函数的振荡边界条件。实施例1：三维连续介质稳定流模型研究区ω为10km×10km×10m的区域，原点为(50m,50m,0m)渗透系数kx＝ky＝kz＝10-8x2m/d，研究方程为稳定流方程：边界条件和源汇项w由解析解h＝10-4(x2+y2+z2)给出。子例1.1：采用fem,msfem和etmsfem求解，并将研究区剖分为相同数目的细单元；fem将研究区剖分为120×120×2的网格，其他方法将研究区剖分为30×30×2的网格；msfem将每个粗单元剖分为4×4×1的网格以获得细单元，etmsfem将每个粗单元剖分为2×2×1的网格获得中单元，再将每个中单元被剖分为2×2×1的网格获得细单元。图2为as、fem、msfem和etmsfem在y＝4050m，z＝5m平面上的水头场，可以看出几种方法获得的水头场十分接近，证明了在细单元数目相同时etmsfem可以获得和fem、msfem相近的精度。同时，fem，msfem和etmsfem所用的cpu时间分别为922s、13s、11s，证明了msfem和etmsfem比fem更加高效。在获得水头场之后，我们将比较etmsfem和method-yeh求解达西速度的能力。其中，method-yeh将使用fem的网格剖分和获得的水头值。as、method-yeh和etmsfem在y＝4050m，z＝5m平面上的粗尺度达西速度场如图3所示，可以看出method-yeh和etmsfem的解十分相近且精度很高。在获得粗尺度达西速度后etmsfem可以通过三维多尺度基函数插值得到细尺度达西速度，因此etmsfem获得的达西速度的数目和method-yeh相同。etmsfem共需28s来求解水头和所有达西速度的值，而method-yeh则需要51241s来求解水头和达西速度，显示了etmsfem的cpu时间不到method-yeh的0.05％。这一结果证明了etmsfem能够高效的求解达西速度，且具有较高的精度。子例1.2：为了更好的展示etmsfem构造基函数的效率，msfem和etmsfem将研究区剖分为50×50×2的网格，msfem将每个粗单元剖分为12×12×4的网格以获得细单元，etmsfem将每个粗单元剖分为3×3×2的网格获得中单元，再将每个中单元被剖分为4×4×2的网格获得细单元。上述两方法在y＝4050m，z＝5m处的获得水头相对误差值如图4所示，可以看出两方法的相对误差值均低于0.003％，etmsfem的结果略好。etmsfem仅仅使用了1222s的cpu时间，而msfem则需要2213s，显示了etmsfem能够在保证精度的前提下大幅降低计算消耗。子例1.3：本子例是为了检验etmsfem所求解的达西速度是否满足质量守恒性。etmsfem将研究区剖分为80×80×40的网格，并使用子例1.1中的细网格剖分。在研究区中我们选取了两个1km×1km×1m大小的局部子区域，原点分别为(2050m,2050m,2m)和(6050m,6050m,6m)。在整个研究区和两个子区域上考虑质量守恒方程：式中ω0为所考虑的区域，vh为h＝x,y,z方向的达西速度，n为外法线方向，w为源汇项；此式右端项有解析表达式，我们将其作为标准值进行参照。我们使用as和etmsfem在网格上的粗尺度节点上的达西速度值计算等式左端项，并和标准值对比，获得的相对误差值如下：表1方法区域1区域2全局etmsfem0.13％0.02％0.56％as0.14％0.03％0.25％如上表所示，etmsfem和as的相对误差值十分接近，显示了这些相对误差值主要是由网格剖分产生的。同时，所有的相对误差值均在0.6％以下，证明了etmsfem的全局和局部守恒的误差很小。etmsfem和as的全局误差大于局部误差，这是因为本例中的渗透系数在右边界处变化最为剧烈，获得的达西速度值的误差也最大。但是在研究区内部所有1km×1km×1m大小的子区域中，etmsfem最大的相对误差值仅为3.3％，而as为2.16％。实施例2：三维随机对数正态分布介质稳定流模型研究区ω为1km×1km×120m的区域，原点为(0m,0m,0m)。渗透系数kx＝ky＝kz＝k，其中k是由gslib(deutschandjournel,1998)中的序贯高斯模拟法在400×400×8的网格上生成的随机对数正态分布系数场，lnk的方差为4，相关长度为100m。研究区的左右边界为定水头边界，分别为16m和11m，其他边界隔水，源汇项为0。采用msfem和etmsfem求解本例，并将研究区剖分为相同数目的细单元。msfem和etmsfem将研究区剖分为25×25×2的网格。同时我们还采用了两种粗单元剖分，1：msfem将每个粗单元剖分为16×16×4的网格以获得细单元，etmsfem将每个粗单元剖分为4×4×2的网格获得中单元，再将每个中单元被剖分为4×4×2的网格获得细单元；2：msfem将每个粗单元剖分为4×4×1的网格以获得细单元，etmsfem将每个粗单元剖分为2×2×1的网格获得中单元，再将每个中单元被剖分为2×2×1的网格获得细单元。由于本例没有解析解，fem将研究区剖分为400×400×8的网格，作为标准解(truesolution)。msfem和etmsfem以及truesolution在y＝520m，z＝60m截面处的水头值如图5所示。从图中可以看出，msfem和etmsfem的在采用第一种(较密)的粗单元剖分时精度较高，和truesolution吻合的很好；两种方法在采用第二种(较粗)的粗单元剖分时精度略低于第一种。这一结果证明了etmsfem能够较好的处理随机对数正态分布介质，获得的精度与msfem、fem相近。同时，etmsfem的粗单元剖分和msfem的粗单元剖分加密效果相同。同时，etmsfem仅使用了322s的cpu时间，大约是msfem消耗的cpu时间(566s)的一半，显示了etmsfem具有很高的计算效率，能够大幅降低计算消耗。实施例3：三维水平渐变垂向突变介质非稳定流模型考虑如下三维非稳定流方程：研究区ω为10km×10km×120m的区域，原点为(0m,0m,0m)，共含有4个含水层和4个若透水层；在含水层的渗透系数kx＝ky＝1+x/50m/d，弱透水层的渗透系数kx＝ky＝0.005+x/10000m/d，垂向渗透系数为水平方向的十分之一；贮水系数为s＝5×10-10x/m,左右边界为定水头边界，水头值分别为10m和1m，其他边界为隔水边界，源汇项为0，时间步长为1天，总时间为6天。初始时刻水头线性变化，为h0＝10-x/10000m。采用msfem和etmsfem求解本例，并将研究区剖分为相同数目的细单元；msfem和etmsfem将研究区剖分为30×30×2的网格；msfem将每个粗单元剖分为16×16×6的网格以获得细单元，etmsfem将每个粗单元剖分为8×8×2的网格获得中单元，再将每个中单元被剖分为2×2×3的网格获得细单元；由于本例没有解析解，msfem将研究区剖分为60×60×2的网格，粗单元剖分不变，作为标准解(truesolution)。图6为各数值方法在y＝5000m和z＝60m处的水头值，可以看出msfem和etmsfem的结果十分相近，etmsfem的结果略好。etmsfem使用了5454s求解本例，仅仅为msfem所需时间(11348s)的48％。这一结果再次证明了etmsfem方法的高效。本发明具体应用途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。当前第1页12