基于埃尔米特插值基本加权无振荡格式的全流场模拟方法与流程

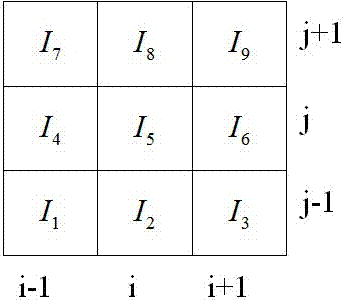
本发明公开了一种基于埃尔米特插值基本加权无振荡格式的全流场模拟方法，涉及计算流体力学工程技术领域。

背景技术：

在计算流体力学数值模拟中，高精度格式的构造及其应用一直是研究的重点内容，因为高精度格式能够对全流场进行精确模拟，能够很好的模拟出解的结构以及准确的捕捉激波位置。1983年，harten首次提出了tvd(totalvariationdiminishing)格式，并在此基础上与osher于1987年提出了eno(essentiallynon-oscillatory)高精度格式，eno格式的主要思想是在逐次扩展的模板中选出最光滑的模板来构造多项式求出单元边界处的值，进而达到高精度、高分辨率和在间断处基本无振荡的效果。但是，在方法的实现过程中，eno格式会造成计算结果的浪费，导致计算效率不高，因此，liu，osher和chan等提出了weno(weightedessentiallynon-oscillatory)格式，提高了计算结果的利用率并且使得r阶精度的eno格式提高到r+1阶精度。1996年，jiang和shu提出了一种新的weno格式，使得数值精度能够提高到2r-1阶。随后，qiu和shu发展了此类方法，命名为hweno格式并将其作为限制器用于rkdg(runge-kuttadiscontinuousgalerkin)方法。来年，他们将这种方法推广到二维情形。2008年，zhu和qiu构造出具有四阶精度的有限体积hweno格式。这些经典的数值计算方法对网格质量要求较高，不能直接应用于计算流场中包含复杂物面边界的可压绕流问题，另一方面，非结构网格上的高精度格式构造复杂，所以将高精度格式在笛卡尔网格中实现处理含复杂物面的全流场模拟问题是有必要的。对于这些含有复杂几何外形物体的流场数值模拟，由于物面边界与笛卡尔网格相交的任意性，所以在物面边界处会产生解的伪振荡。针对此问题，dadone等系统地研究了贴体网格中复杂几何外形的物面边界处理方法，将其命名为st(symmetrytechnique)方法和ccst(curvaturecorrectedsymmetrytechnique)方法，并将这些浸入边界方法推广到了非贴体的笛卡尔网格中，命名为gbcm(ghostbody-cellmethod)方法。另外，forrer等于1998年提出了一种浸入边界法，命名为fgcm(forrer’sghostcellmethod)方法。这些方法均能有效处理复杂物面边界条件，能有效降低所用计算网格的生成难度。

另外，一阶精度的数值方法在捕捉激波时不会出现非物理的数值振荡但会过度抹平强间断，而往往强间断对问题的后续研究有着重要意义，因此引进高精度数值计算格式进行相关数值模拟是有必要的。当计算区域中出现复杂物面时，许多基于结构网格设计出来的高精度计算格式不能直接应用于相关数值计算，需要先生成复杂的贴体网格，再构造出基于此贴体网格的高精度计算格式，步骤复杂繁琐，推广困难。

技术实现要素：

本发明的针对现有技术中的不足，提供一种基于埃尔米特插值基本加权无振荡格式的全流场模拟方法，能针对各种复杂物体绕流问题，全流场统一采用笛卡尔网格和高精度计算格式进行数值模拟。本发明首先给出笛卡尔网格下有限体积robusthweno高精度数值计算格式的构造，此格式能更好地推广到高维情形以及自适应和移动网格情形，随后针对笛卡尔网格的非贴体特性，采用合适的边界处理方法处理物面边界条件，能将这二者有效结合并应用于具有复杂几何外形物面的无粘可压缩绕流问题的数值模拟。相比于weno格式，hweno格式通过hermite插值方法构造多项式，既需要函数值又需要其导数值，因此加强了各个网格单元之间的联系，使得格式更加紧凑和稳定，而robusthweno格式相对于hweno格式增强了格式的鲁棒性，能够更好地推广。

为实现上述目的，本发明采用以下技术方案：

在笛卡尔坐标下，流场计算区域内含有物体，先通过虚拟单元浸入边界法对物体内的网格点进行赋值形成全流场，然后利用robusthweno格式对全流场进行数值模拟，具体步骤包括：

1)利用虚拟单元浸入边界法对物体内部的网格单元点进行赋值，使含有物体的流场形成单一介质的全流场；

2)建立无粘流体的控制方程，所述控制方程是一个关于时间变量t和关于空间变量x，y的方程组，对控制方程空间变量进行离散得到半离散的有限体积格式，具体步骤如下：

1.1分别对空间变量x，y求导得到方程组，增加控制方程的数量；

1.2对控制方程两边同时在目标单元上进行积分得到有限体积格式，所述有限体积格式包含时间导数项和空间积分项；

1.3对所述空间积分项利用gauss求积公式求解从而得到关于时间导数项的半离散有限体积格式；

3)对时间变量使用三阶tvdrunge-kutta离散公式从而将半离散有限体积格式变成时空全离散有限体积格式；

4)根据时空全离散有限体积格式得到下一时间层上的流场值，依次迭代，得到全流场稳定时的数值模拟。

为优化上述技术方案，采取的具体措施还包括：

步骤1)中，利用st和fgcm两种虚拟单元方法处理物面边界条件，使得流场近似为单一介质的全流场，具体步骤包括：

a、先对计算区域内的点进行分类，分为物体内部的虚拟单元点和物体外部点；

b、找到所有虚拟单元点关于物面的对称点，确定对称点落入的最近网格单元i1，以及其上下左右的网格单元i2，i3，i4，i5；

c、利用网格单元i1，i2，i3，i4，i5上的流场值，通过插值公式，确定对称点流场值；

d、通过st和fgcm虚拟单元方法，得到关于虚拟单元点和对称点的物理量关系，从而得到虚拟单元点的流场值，将含有物体的流场形成成单一介质的全流场。

步骤1.1中，控制方程为：

其中，u＝(ρ，ρu，ρv，e)^t表示守恒变量，f(u)＝(ρu，ρu²+p，ρuv，u(e+p))^t，g(u)＝(ρv，ρuv，ρv²+p，v(e+p))^t，f(u)，g(u)表示通量，ut表示u对t求导，f(u)x表示f(u)对x求导，g(u)y表示g(u)对y求导，ρ，p，u，v，e分别表示流体密度、压强、水平方向速度、竖直方向速度和能量，t表示转置，u0表示初始状态值；

对控制方程分别对空间变量x和y求导得到方程：

其中，表示u对x求导，表示u对y求导，h(u，v)x和q(u，w)x表示h(u，v)q(u，w)分别对x求导，r(u，v)y和s(u，w)y表示r(u，v)s(u，w)分别对y求导，h(u，v)＝f′(u)v，r(u，v)＝g′(u)v，q(u，w)＝f′(u)w，s(u，w)＝g′(u)w，f′(u)，g′(u)分别表示f(u)，g(u)对u求导。

步骤1.2中，对控制方程在目标单元iij内积分有：

其中，表示u对x求导，表示u对y求导，h(u，v)x和q(u，w)x表示h(u，v)q(u，w)分别对x求导，r(u，v)y和s(u，w)y表示r(u，v)s(u，w)分别对y求导，h(u，v)＝f′(u)v，r(u，v)＝g′(u)v，q(u，w)＝f′(u)w，s(u，w)＝g′(u)w，f′(u)，g′(u)分别表示f(u)，g(u)对u求导。

步骤1.3中，利用gauss求积公式求解，具体过程如下：

a、在目标单元边界上取8个gauss点，分别为和并将目标单元及周围共9个单元组成母模板；

b、在母模板中选取8个子模板，每个子模板必须包括目标单元；

c、利用hermite插值方法在8个子模板中求出目标单元每个gauss点的重构多项式pl(x，y)，l＝1，…，8，其中l表示对应子模板序号，则有：

其中，分别代表u在网格单元ii-1，j-1、ii，j-1、ii+1，j-1、ii-1，j、iij、ii+1，j、ii-1，j+1、ii，j+1、ii+1，j+1的平均值，分别代表v在网格单元ii-1，j、ii+1，j的平均值，分别代表w在网格单元ii，j-1、ii，j+1的平均值，h为网格步长；

d、取线性权γl，计算光滑指示器βl，用于衡量重构多项式pl(x，y)，l＝1，…，8在目标单元上的光滑程度，计算公式为：

其中，α为多重指标，d是求导算子，r是多项式pl(x，y)的最高次数；

e、计算非线性权ωl，其计算公式为：

其中，为计算过程中的过渡值，βl为光滑指示器，ε＝10^-6；

f、求出u在每个gauss点gk处的近似表达式为：

其中gk表示第k个gauss点，k＝1，…，8；

g、重复步骤c到步骤f，求出v，w在每个gauss点gk处的近似表达式；

h、利用gauss求积公式求解：

其中，表示目标单元的边界长度，ak为gauss求积公式的权重系数，为单位外法向向量，和用数值通量代替；

i、将计算结果代入含有时间导数项的半离散有限体积格式，得到关于时间导数的常微分方程。

步骤3)中，三阶tvdrunge-kutta离散公式为：

其中，为中间过渡值，δt为时间步长，上标n表示第n时间层，为积分近似值。

步骤4)中，所述时空全离散有限体积格式为关于时间层的迭代公式，初始状态值已知，通过迭代公式求出下一时间层的流场值，依次得到稳定时的全流场数值模拟。

本发明的有益效果是：将笛卡尔网格下有限体积robusthweno格式与浸入边界虚拟单元方法结合，应用于具有复杂几何外形的无粘流动问题数值模拟中，这样避免了复杂网格的生成和非结构网格下高精度格式的构造，而相比于weno格式和hweno格式，robusthweno格式增强了格式的紧凑性和鲁棒性，并且可以很好地推广到更高维的和移动网格下的数值模拟中。传统的数值方法在解决具有真实斜面的双马赫反射问题，圆柱绕流问题和翼型绕流问题时需要将做一定的等价转化甚至是无法解决的，但本发明能稳健，准确，基本无振荡地捕捉到强激波和接触间断并同时在解的光滑区域保持时空一致高阶精度。

附图说明

图1是大模板t示意图。

图2是笛卡尔网格中网格单元与物面边界相交示意图。

图3a-3b是实施例一中，前台阶问题分别采用st和fgcm两种边界处理方法的密度等值线图。

图4a-4b是实施例一中，前台阶问题分别采用st和fgcm两种边界处理方法的压强等值线图。

图5a-5b是实施例二中，双马赫问题分别采用st和fgcm两种边界处理方法的密度等值线图。

图6a-6b是实施例二中，双马赫问题分别采用st和fgcm两种边界处理方法的压强等值线图。

图7a-7b是实施例三中，圆柱绕流问题分别采用st和fgcm两种边界处理方法的密度等值线图。

图8a-8b是实施例三中，圆柱绕流问题分别采用st和fgcm两种边界处理方法的马赫数等值线图。

图9a-9b是实施例四中，naca0012翼型绕流问题分别采用st和fgcm两种边界处理方法的压强等值线图。

图10a-10b是实施例四中，naca0012翼型绕流问题分别采用st和fgcm两种边界处理方法的翼型表面压力系数图。

具体实施方式

现在结合附图对本发明作进一步详细的说明。

一、有限体积ronusthweno格式的构造

考虑二维euler方程：

其中，t表示时间变量，x，y表示空间变量，u＝(ρ，ρu，ρv，e)^t表示守恒变量，f(u)＝(ρu，ρu²+p，ρuv，u(e+p))^t，g(u)＝(ρv，ρuv，ρv²+p，v(e+p))^t，f(u)，g(u)表示通量，f(u)x表示f(u)对x求导，g(u)y表示g(u)对y求导，ρ，p，u，v，e分别表示流体密度、压强、水平方向速度、竖直方向速度以及能量，t表示转置，u0表示初始状态值。

假设网格单元步长是固定的，xi+1/2-xi-1/2＝δx，yj+1/2-yj-1/2＝δy，网格中心为网格单元为iij＝[xi-1/2，xi+1/2]×[yj-1/2，yj+1/2]，其中下标i、j为坐标序号。

对方程(1)求导有：

其中，表示u对x求导，表示u对y求导，h(u，v)x和q(u，w)x表示h(u，v)q(u，w)分别对x求导，r(u，v)y和s(u，w)y表示r(u，v)s(u，w)分别对y求导，其中h(u，v)＝f′(u)v，r(u，v)＝g′(u)v，q(u，w)＝f′(u)w，s(u，w)＝g′(u)w，f′(u)，g′(u)分别表示f(u)，g(u)对u求导。

定义表示u在网格单元iij内的平均值，表示v在网格单元iij内的平均值，表示w在网格单元iij内的平均值，即

首先，求每个gauss点gk处u(gk，t)，v(gk，t)，w(gk，t)的值，具体步骤如下：

步骤1，如图1所示，将目标单元iij以及周围共9个网格单元组成一个母模板，且假设网格步长都为h，如图1，其中i5为目标单元iij，并记分别代表u，v，w在网格单元im的平均值(m＝1，…，9)。

步骤2，在母模板中选择8个子模板分别为：s1＝{i1，i2，i4，i5}，s2＝{i2，i3，i5，i6}，s3＝{i4，i5，i7，i8}，s4＝{i5，i6，i7，i9}，s5＝{i1，i2，i3，i4，i5，i7}，s6＝{i1，i2，i3，i5，i6，i9}，s7＝{i1，i4，i5，i7，i8，i9}，s8＝{i3，i5，i6，i7，i8，i9}，其中ii为对应序号的网格单元。

步骤3，在每个子模板中分别求出每个gauss点gk处u，v，w的重构多项式pn(x，y)，n＝1，…，8。

步骤3.1，u的重构多项式pn(x，y)，n＝1，…，8求解过程如下：

步骤3.1.1，在子模板s1，s2，s3，s4上构造多项式pn(x，y)，n＝1，…，4，使其满足：

其中

n＝1，k＝1，2，4，5，kx＝4，ky＝2；n＝2，k＝2，3，5，6，kx＝6，ky＝2；

n＝3，k＝4，5，7，8，kx＝4，ky＝8；n＝4，k＝5，6，8，9，kx＝6，ky＝8；

步骤3.1.2，在子模板s5，s6，s7，s8上构造多项式pn(x，y)，n＝5，…，8，使其满足：

其中

n＝5，k＝1，2，3，4，5，7；n＝6，k＝1，2，3，5，6，9；

n＝7，k＝1，4，5，7，8，9；n＝8，k＝3，5，6，7，8，9；

步骤3.1.3，得到每个子模板在每个gauss点gk处的插值多项式pn(x，y)，n＝1，…，8，如下：

步骤3.2，v的重构多项式pn(x，y)，n＝1，…，8求解过程如下：

步骤3.2.1，在子模板s1，s2，s3，s4上构造多项式pn(x，y)，n＝1，…，4，使其满足：

n＝1，k＝1，2，4，5，kx＝1，4，5，ky＝1，2，5；n＝2，k＝2，3，5，6，kx＝3，5，6，ky＝2，3，5；

n＝3，k＝4，5，7，8，kx＝4，5，7，ky＝5，7，8；n＝4，k＝5，6，8，9，kx＝5，6，9，ky＝5，8，9；

步骤3.2.2，在子模板s5，s6，s7，s8上构造多项式pn(x，y)，n＝5，…，8，使其满足：

其中

n＝5，kx＝1，2，3，4，5，7；n＝6，kx＝1，2，3，5，6，9；

n＝7，kx＝1，4，5，7，8，9；n＝8，kx＝3，5，6，7，8，9；

步骤3.2.3，得到每个子模板在每个gauss点gk处的插值多项式pn(x，y)，n＝1，…，8，如下：

其中，表示pn(x，y)对x求偏导(n＝1，…，4)，h为步长；

步骤3.3，w的重构多项式pn(x，y)，n＝1，…，8求解过程如下：

步骤3.3.1，在子模板s1，s2，s3，s4上构造多项式pn(x，y)，n＝1，…，4，使其满足：

其中

n＝1，k＝1，2，4，5，kx＝1，4，5，ky＝1，2，5；n＝2，k＝2，3，5，6，kx＝3，5，6，ky＝2，3，5；

n＝3，k＝4，5，7，8，kx＝4，5，7，ky＝5，7，8；n＝4，k＝5，6，8，9，kx＝5，6，9，ky＝5，8，9；

步骤3.3.2，在子模板s5，s6，s7，s8上构造多项式pn(x，y)，n＝5，…，8，使其满足：

其中

n＝5，ky＝1，2，3，4，5，7；n＝6，ky＝1，2，3，5，6，9；

n＝7，ky＝1，4，5，7，8，9；n＝8，ky＝3，5，6，7，8，9；

步骤3.3.3，得到每个子模板在每个gauss点gk处的插值多项式pn(x，y)，n＝1，…，8，如下：

其中，表示pn(x，y)对y求偏导(n＝1，…，4)，h为步长。

步骤4，取每个gauss点gk处的线性权为

步骤5，计算光滑指示器βl，l＝1，…，8，计算公式如下：

步骤5.1，重构u的光滑指示器计算公式为：

步骤5.2，重构v的光滑指示器计算公式为：

步骤5.3，重构w的光滑指示器计算公式为：

其中，a是多重指标，|i5|是目标单元的面积，d是求导算子，下标l是子模板对应的序号。

步骤6，通过线性权gl和光滑指示器βl计算非线性权ωl：

其中，为计算中的过渡值，βl为光滑指示器，ε取值10^-6，防止分母为零。

步骤7，进一步得到u，v，w在每个gauss点gk处的近似值：

其中，表示pl(gk)对x求偏导，表示pl(gk)对y求偏导，pl(gk)表示将gauss点的坐标gk代入相应多项式pl(x，y)后的取值；

其次，对方程(1)、(2)、(3)在目标单元iij内积分得到半离散的有限体积格式如下：

其中，表示u在网格单元iij内的平均值，表示v在网格单元iij内的平均值，表示w在网格单元iij内的平均值，即f＝(f(u)，g(u))^t，h＝(h(u，v)，r(u，v))^t，q＝(q(u，w)，s(u，w))^t，t表示转置，为外法向向量，等式右边的积分项可用q点gauss求积公式求得，如下：

其中，表示目标单元的边界长度，ak为gauss求积公式的权重系数，为单位外法向向量，用数值通量代替；

最后，利用三阶tvdrunge-kutta离散公式：

得到时空全离散有限体积格式，其中为中间过渡值，δt为时间步长，上标n表示第n时间层，为积分近似值。

二、虚拟单元方法

在实际计算当中，由于笛卡尔网格的非贴体性，有限体积robusthweno格式在处理复杂几何外形的物面可压绕流问题时非常困难，在网格和物面的相交处会产生非物理振荡。为弥补这个不足，本发明采用浸入边界法处理物面边界。如图2所示，实心三角形表示物面内部虚拟网格单元点，实心正方形表示虚拟网格单元点关于物面边界的对称点。

我们需要通过物面边界条件以及动量关系等利用流体内b点的值确定物体内a点值，进而进行全流场的数值模拟。下面介绍两种不同的方法确定a点流场值和b点流场值之间的关系并进行数值实验，数值模拟出计算区域内包含复杂几何外形物面的全流场。

2.1、st(symmetrytechnique)方法

这种方法是确定a点和b点流场值最简单最直接的方法，计算公式如下：

上式中r为密度，p为压强，为速度矢量，表示物面处的单位外法线向量，这样给出的边界条件可以满足壁面无穿透条件。

2.2、fgcm(forrer’sghostcellmethod)方法

forrer等提出了一种虚拟单元浸入边界法，其思想是a点的速度仍然使用一般的对称反射，而密度和压强通过以下公式求得：

其中，xw为过a点的法向向量与物面边界相交的点，为物面的单位外法向量，同样地，这样给出的边界条件也满足壁面无穿透条件。

三、有限体积robusthweno格式与虚拟单元方法的结合

由以上格式的构造步骤可知，有限体积robusthweno格式是一种有限体积高精度数值计算格式。有限体积方法从积分守恒形式的流体方程出发，通过对网格单元上的方程进行离散来构造积分型离散方程。相比于有限差分方法，有限体积方法在网格处理上更加灵活，守恒性好。但是，对于在笛卡尔结构网格上构造的有限体积robusthweno格式，在求解双马赫反射、圆柱绕流等复杂界面绕流问题时是困难的。因为有限体积加权基本无振荡格式在对网格单元流场值进行多项式重构时需要用到周围(包括自身)一共9个网格单元，尤其在网格与物面边界相交的地方，网格与物面以任意形式相交，问题就显得尤为突出。面对这些问题，在双马赫反射数值模拟中，传统的解决办法是使入射激波倾斜，斜面便与网格线重合，数值模拟就变得清晰而简单了。这样虽然能较好地捕捉到激波的反射情况，但和实验模拟无论是在形式上还是本质上都是有不同的。而在圆柱绕流问题或者是翼型绕流问题中，传统的解决办法是采用混合网格或者非结构网格，这都无疑增大了网格生成的难度以及对应网格上格式构造的难度。本发明将结构网格有限体积robusthweno格式同浸入边界虚拟单元方法结合，有效模拟了具有真实斜面的双马赫反射问题，精确地捕捉了激波与斜面作用后反射的情况。同样地，在高马赫数圆柱绕流和翼型中也得到了较好的数值模拟结果。

下面给出四个算例作为本发明所公开方法的具体实施例。

实施例一、台阶问题。该问题是emery于1968年提出的一个用于检验非线性双曲型守恒律格式的经典算例。初始数据为水平来流马赫数为3，密度为1.4，压强为1，管道区域为[0，3]′[0，1]，在距离左边界0.6处有一高度为0.2的台阶，且台阶延伸到管道的尽头。上下边界为反射边界，左边界为来流边界，右边界为出流边界。图3a-3b和图4a-4b分别给出了t＝4时刻的密度和压强的等值线图。

实施例二、斜面双马赫反射问题。该问题是描述一个强激波入射在与平面成30°角的斜坡上后发生的变化，来流是马赫数为10的强激波。计算区域取[0，3]′[0，2]，始于激波垂直于x轴，初始数据为：

其中的左右状态为ul＝(8，66.009，0，563.544)^t，ur＝(1.4，0，0，2.5)^t，边界条件处理为左右边界分别取左右状态值。下边界：当时，设为反射边界；当时，设为左状态。上边界：当x＞g(t)时，取右状态；当时，取左状态，其中图5a-5b和图6a-6b分别给出了t＝0.2时刻密度和压强的等值线图。

实施例三、圆柱绕流问题。考虑超音速无黏流体流向直径为1的圆柱，初始数据为水平来流马赫数为3，密度为1，压强为1，计算区域为[-10，10]？[10，10]，左边界为来流边界，右边界为超音速出流边界。图7a-7b和图8a-8b分别给出了在计算区域内两种方法得到的密度和马赫数等值线。

实施例四、naca0012翼型跨声速绕流问题。来流马赫数为0.8，攻角a＝1.25度。图9a-9b和图10a-10b分别给出了st方法和fgcm方法压强等值线图和翼型表面压力系数图以及残差图，从图中可以看出有限体积robusthweno格式结合两种浸入边界方法能够很好的捕捉到激波的位置以及激波的强弱，上表面形成一道强激波，下表面形成一道弱激波。

以上仅是本发明的优选实施方式，本发明的保护范围并不仅局限于上述实施例，凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理前提下的若干改进和润饰，应视为本发明的保护范围。