一种基于广义傅里叶级数构建改进微分求积法的方法与流程

本发明涉及数值求解技术领域，特别是涉及一种基于广义傅里叶级数构建改进微分求积法的方法。

背景技术：

目前，在工程和科学领域里，求解线性、非线性方程或方程组是一项很重要的任务。由于只有少数情况能得到解析解，所以大家把重点均放在求其近似解或数值解上。微分求积法在1971年提出，由于其较高的计算精度和效率，越来越受到人们的重视。但是微分求积法存在一些缺陷，即在处理结构振动方程的弹性边界时存在处理不精确，导致求解误差，求解结果准确性较低。

在处理结构弹性边界的方法中，2000年美国韦恩州立大学Li.W.L.教授在杂志《Journal of Sound and Vibration》中第237卷中发表文章《Free vibrations of beams with general boundary conditions》提出了广义傅里叶级数，即在传统傅里叶级数的基础上加上附加项，用于满足结构边界处的不连续，此方法成功解决了弹性边界条件下梁的横向自由振动振动，2007年，杜敬涛在杂志《Journal of Sound and Vibration》第306卷中发表文章《An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges》，此文章利用广义傅里叶级数方法解决了弹性边界矩形板的振动问题。

目前还没有广义傅里叶级数和微分求积法相结合的技术出现以及相关文献报道。

技术实现要素：

本发明的目的是提供一种基于广义傅里叶级数构建改进微分求积法的方法，以实现提高求解结果准确性。

为解决上述技术问题，本发明提供一种基于广义傅里叶级数构建改进微分求积法的方法，该方法包括：

将需要求解的函数表示成傅里叶级数，并在傅里叶级数的基础上加上附加项；

根据边界条件，确定附加项系数和傅里叶级数系数之间的关系；

将求解域离散成独立点，把带有附加项的傅里叶级数代入各个独立点，形成各傅里叶级数系数之间的关系矩阵；

根据所述关系矩阵求解出傅里叶级数系数，确定需要求解的函数。

优选的，附加项系数由边界条件决定。

优选的，所述需要求解的函数包括结构弹性边界约束条件的微分方程。

优选的，所述边界条件为弹性边界条件。

优选的，所述将求解域离散成独立点，包括：

对所求解的函数区间进行离散，选取独立点。

优选的，所述把带有附加项的傅里叶级数代入各个独立点，形成各傅里叶级数系数之间的关系矩阵，包括：

把带有附加项的傅里叶级数代入各个独立点，得到各个独立点对应的方程，形成方程组；

将方程组整理成矩阵形式，得到矩阵方程。

优选的，所述矩阵方程中的未知系数为傅里叶级数系数。

本发明所提供的一种基于广义傅里叶级数构建改进微分求积法的方法，将需要求解的函数表示成傅里叶级数，并在傅里叶级数的基础上加上附加项；根据边界条件，确定附加项系数和傅里叶级数系数之间的关系；将求解域离散成独立点，把带有附加项的傅里叶级数代入各个独立点，形成各傅里叶级数系数之间的关系矩阵；根据所述关系矩阵求解出傅里叶级数系数，确定需要求解的函数。可见，将微分求积法在求解微分方程时的精确性和高效性同广义傅里叶级数在处理结构弹性边界条件的灵活性相结合，所构造的改进微分求积法将在保证计算精度的同时很好的解决结构弹性边界微分方程的求解，实现提高求解结果准确性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据提供的附图获得其他的附图。

图1为本发明所提供的一种基于广义傅里叶级数构建改进微分求积法的方法的流程图；

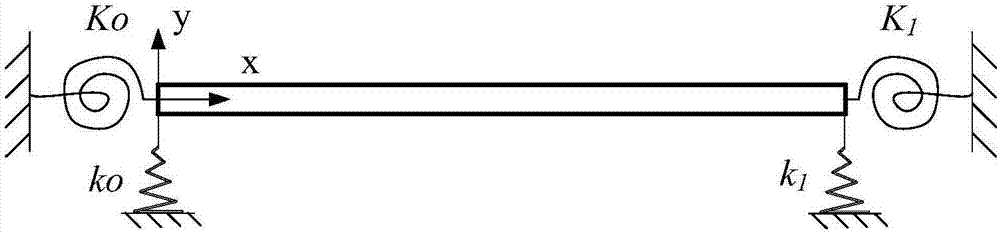
图2为弹性边界梁示意图。

具体实施方式

本发明的核心是提供一种基于广义傅里叶级数构建改进微分求积法的方法，以实现提高求解结果准确性。

为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

请参考图1，图1为本发明所提供的一种基于广义傅里叶级数构建改进微分求积法的方法的流程图，该方法包括：

S11：将需要求解的函数表示成傅里叶级数，并在傅里叶级数的基础上加上附加项；

S12：根据边界条件，确定附加项系数和傅里叶级数系数之间的关系；

S13：将求解域离散成独立点，把带有附加项的傅里叶级数代入各个独立点，形成各傅里叶级数系数之间的关系矩阵；

S14：根据所述关系矩阵求解出傅里叶级数系数，确定需要求解的函数。

可见，将微分求积法在求解微分方程时的精确性和高效性同广义傅里叶级数在处理结构弹性边界条件的灵活性相结合，所构造的改进微分求积法将在保证计算精度的同时很好的解决结构弹性边界微分方程的求解，实现提高求解结果准确性。

基于上述方法，具体的，附加项系数由边界条件决定。其中，在傅里叶级数的基础上加上附加项就构成了广义傅里叶级数。

进一步的，所述需要求解的函数包括结构弹性边界约束条件的微分方程。

其中，所述边界条件为弹性边界条件。

进一步的，步骤S13中，所述将求解域离散成独立点的过程具体为：对所求解的函数区间进行离散，选取独立点。

进一步的，步骤S13中，把带有附加项的傅里叶级数代入各个独立点，形成各傅里叶级数系数之间的关系矩阵的过程具体为：把带有附加项的傅里叶级数代入各个独立点，得到各个独立点对应的方程，形成方程组；将方程组整理成矩阵形式，得到矩阵方程。

其中，所述矩阵方程中的未知系数为傅里叶级数系数。矩阵方程为微分方程对应的矩阵方程。

具体的，将微分方程中所求函数表述成傅里叶级数加上附加项的形式，其中附加项的系数由边界条件决定。对所求区间进行离散，选取独立点。将广义傅里叶级数带入各离散独立点，得到各个独立点对应的方程。将方程组整理成矩阵形式，得到微分方程对应的矩阵方程，方程中未知系数即傅里叶级数系数。

其中，根据弹性边界条件控制方程确定附加项系数同傅里叶级数系数间的关系。将附加项级数用傅里叶级数的系数表示，并将所求函数表示成只含傅里叶级数系数的形式。将所求函数区间离散成各个独立点。将广义傅里叶级数带入各离散独立点，带进各离散独立点，得到关于傅里叶级数系数的方程组。求解方程组，得到傅里叶系数，从而确定所求函数。

详细的，提供本方法应用于两端弹性约束梁控制微分方程求解的例子。基于本方法，需要求解的函数为梁的振动控制方程。

例如，图2所示梁的振动控制方程是：

边界条件是：

Dy”＝K₀y' Dy”'＝-k₀y x＝0 (2a)

Dy”＝K₁y' Dy”'＝-k₁y x＝L (2b)

其中D＝EI，设梁的位移函数为：

其中ξ_i(x)为容许函数，吸收傅里叶级数方法边界不连续，加快傅里叶级数的收敛性。

将梁的位移函数带进边界条件，得到如下式子：

其中参数C₁…C₈为：

将式(5)写成如下的矩阵形式：

其中，Q_m和A的表达式如下：

A＝{a₀ a₁ a₂ … a_M}^T (9)

令R如下：

则得到：

从式(11)可以看出，系数b和a不是独立的变量，系数b可以由系数a根据边界条件得到，将式(11)带进方程(3)消掉系数b，则梁的位移函数可以表示为：

方程(12)为弹性边界条件下梁的位移函数表达式，此表达式已经包含了在4个弹簧约束下梁的位移函数，并且可以对方程(12)逐项求导数。

根据DQ原理，在梁坐标离散，选取N个点，坐标分别为：

0≤x₁＜x₂＜...＜x_n≤L (13)

采用微分求积法常采用的Chebyshev-Gauss点作为离散点，即：

对式(12)求r阶导数并将点x_i带入，得到：

通过上式可以看出，函数y(x)在点x_i处的r阶导数值可以由系数a_m加权求和得到，原理类似于传统的微分求积法，此处称为改进微分求积法。

将上式带进梁的振动方程，并取所有的N个点，得：

将方程(16)简写为：

方程(17)为标准的振动方程，求解方程(17)的特征值和特征向量即得到梁的固有频率和位移系数a_m，从而确定梁的振型。

根据以上推导，对一根梁在不同边界条件下(固支-固支、简支-简支、弹性-弹性)进行验算，其参数为：长度为L＝1m；横截面积A＝7.854e^-5m²；惯性矩I＝4.9087e^-10m⁴；密度＝7850kg/m³,杨氏模量E＝2.1e11N/m²。计算结果如表1-表3所示。表1为固支-固支梁固有频率表格，表2为简支-简支梁固有频率表格，表3为弹性-弹性边界条件下梁无量纲固有频率。

由计算结果可得，在经典边界(固支-固支、简支-简支)情况下，改进微分求积法同传统微分求积法计算结果相差很小；从表3可以看出，改进微分求积法在处理弹性边界条件时计算得到的结果也较为精确。

表1

表2

弹性-弹性边界条件计算结果同参考数据结果比较，结果如表3所示，其中弹簧刚度和固有频率均由无量纲量表示，弹簧刚度为：

无量纲固有频率

表3

详细的，本方法首先将需要求解的函数表示成傅里叶级数并附加容许项，根据边界条件，确定容许项系数同傅里叶级数系数之间的关系。其次将求解域离散成独立点，把带有附加项的傅里叶函数分别代入离散点，形成各傅里叶系数之间的关系矩阵。最后根据傅里叶系数之间的关系求出具体傅里叶系数，从而确定所求函数。本方法具有构造权系数矩阵简单、收敛精度高、计算速度快、适用于弹性边界的优点，实现了广义傅里叶级数同微分求积法的结合，从而使改进微分求积法在保证计算精度的同时很好的解决结构弹性边界条件的微分方程求解。

本发明的优点主要体现在：与微分求积法相比，此改进微分求积法存在两个优点：改进微分求积法在获取权系数矩阵时具有方便快捷的优势；改进微分求积法能很好的处理弹性边界条件；改进微分求积法求得的是傅里叶级数的系数，所求函数可以表示能解析形式，而微分求积法只能求得离散点处的函数值。

以上对本发明所提供的一种基于广义傅里叶级数构建改进微分求积法的方法进行了详细介绍。本文中应用了具体个例对本发明的原理及实施方式进行了阐述，以上实施例的说明只是用于帮助理解本发明的方法及其核心思想。应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以对本发明进行若干改进和修饰，这些改进和修饰也落入本发明权利要求的保护范围内。