一种用于飞机结构件复杂槽腔内面间最短距离计算方法与流程

本发明涉及航空制造中的飞机结构件数控加工领域，具体来说，是一种用于飞机结构件复杂槽腔内面间最短距离计算方法。

背景技术：

在现代飞机设计中，为满足高性能的要求，广泛采用性能优越的整体结构件，然而在结构件三维cad建模中，特别是复杂、超大型以及需要多工位加工的构件，由于种种原因，例如设计方法、设计水平等因素，使得零件的设计模型存在种种缺陷或不规范甚至错误的地方。其中，零件的槽腔内面间最短距离过小是一种常见缺陷，该缺陷会导致致加工区域无法进刀。目前在实际生产中仍大量人工方式对三维设计模型进行检查、修正。而传统人工模型检测存在效率低，可靠性差的固有缺陷，难以保证模型质量，进而影响加工质量和效率、延长生产周期。

技术实现要素：

为了解决上述存在问题，本发明提供一种用于飞机结构件复杂槽腔内面间最短距离计算方法。

本发明的目的是通过下述技术方案实现的：

1)将面转化为线；2)线线之间的距离计算。

所述步骤1)将面转化为线流程包括：

(1)常见槽腔侧面描述与分类：①不含开闭角和内陷的侧面；②全开角侧面；③全闭角侧面；④内陷；⑤混合开闭角侧面；

(2)边集选取：①基础理论；②根据面类型选取边集；③边集离散

所述步骤2)线线之间的距离计算：

(1)有效性判断；(2)直线段与直线段间的距离计算；(3)直线段和圆弧段间的距离计算；(4)圆

弧段间的曲线计算。

通过上述方法，可以实现对飞机结构件复杂槽腔内面间最短距离自动进行计算，极大的提高了检测效率，该方法为下游capp平台提供适于自动编程的有效零件模型迈出了重要一步，对缩短产品研制周期、降低生产成本有着重要的意义。

本发明的有益效果：本发明采用上述提出的一种用于飞机结构件复杂槽腔内面间最短距离计算方法，可以根据面类型选取合适的边集，通过计算边集间的最短距离得出复杂槽腔内面间最短距离。采用这种方法可以快速准确的计算出飞机结构件复杂槽腔内面间最短距离，为飞机结构件三维设计模型质量检测系统的特征识别提供技术支撑。

附图说明

图1最短距离计算算法示意图

图2.a不含开闭角和内陷的侧面结构示意图

图2.b全开角侧面结构示意图

图2.c全闭角侧面示意图

图2.d内陷结构示意图

图2.e混合开闭角侧面结构示意图

图3.a侧位规则示意图

图3.b垂直规则与相邻规则示意图

图3.c凸弧规则示意图

图3.d凹凸性规则示意图

图3.e凹弧侧位规则示意图

图3.f相交规则示意图

图4直线段间最短距离示意图

图5直线段与圆弧之间的最短距离示意图

图6圆弧之间最短距离示意图

具体实施方法

本发明是建立在cad/cam系统平台上，实现飞机结构件复杂槽腔内面间最短距离计算方法。

下面结合附图对本发明的实施实例进行详细的说明，本实施实例是在以发明技术方案为前提下进行实施，给出了详细的实施方式和具体的实现过程。显然，所描述的实施例仅是本发明一部分实施例，而不是全部的实施例。基于本发明的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明的保护范围。

图1所示为本发明提出的飞机结构件复杂槽腔内面间最短距离计算方法实现的具体流程，其实现步骤为：1)将面转化为线；2)距离有效性判断；3)线线之间的距离计算。

步骤1)将面转化为线

(1)常见槽腔侧面描述及分类

①不含开闭角和内陷的普通侧面，如图2.a所示；

②全开角侧面，如图2.b所示；

③全闭角侧面，如图2.c所示；

④内陷，如图2.d所示；

⑤混合开闭角侧面，如图2.e所示；

(2)边集选取

①基础理论：

a.内环和外行

将平面槽腔表示为fp的结构可以由底面集fbf在腹板上投影得到的环lp表示。将最外围的环称为外环，记为lc，定义逆时针方向为内环的正方向；将外环所包围的环称为内环，记为ls，内环的集合记为ls，定义顺时针方向为内环的正方向。则lp可表示为：

lp＝lc∪ls

其中ls为内环的集合，即n为内环的个数。

b.点的凹凸性

对于沿环l正方向排列的三个不重合的点pi、pj、pk，定义向量vz(x,y,z)，令若满足z>0，称pj为凸点，记为px，满足z<0，称pj为凹点，记为pe。，若z＝0，则称pj为切点，记为pt。

c.弧的凹凸性

对于环l上某一圆弧ci，ci上存在一点pi，若pi为凸点，称该ci为凸弧，记为cx，若pi为凹点，称该ci为凹弧，记为ce。

②根据面类型选取边集

对于槽fp内任意侧面fsfi，fsfi与顶面ft的公共边集在腹板fbc的投影称为fsfi的顶边集，记为eti，fsfi与fbf的公共边集在fbc的投影称为fsfi的底边集，记为ebi。易知fsfi、eti、ebi三者是一一对应的关系。

为了简化算法，定义eti与ebi的方向相同,如图3所示。

易知则对于侧面fsfi∈fsf，存在唯一的一个边集与其对应，此时ei＝ebi，将该单射关系记为f，则有：

f(fsfi)＝ei

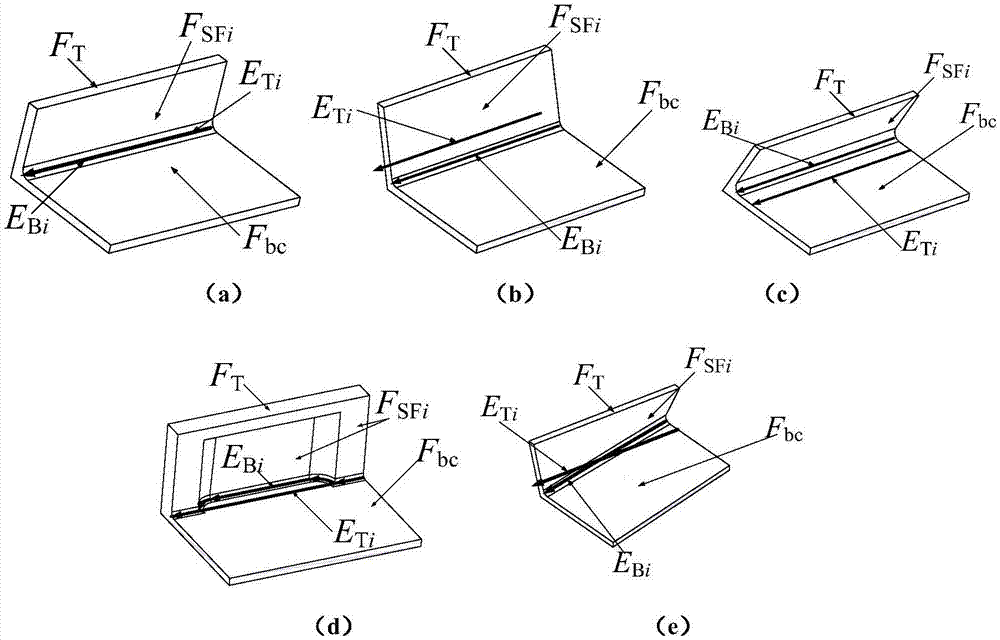
侧面根据其结构特点可以分为不含开闭角和内陷的侧面(一般侧面)、全开角侧面、全闭角侧面、内陷以及混合开闭角侧面，它们的示意图、顶边集与底边集分别如图3(a)、(b)、(c)、(d)、(e)所示。其中一般侧面的顶边集与底边集重合，全开角侧面的顶边集在底边集右侧，全闭角侧面的顶边集在底边集左侧，内陷的顶边集一部分在底边集左侧、一部分与底边集重合，混合开闭角侧面的顶边集一部分在底边集左侧、一部分在底边集右侧。

根据面间最短距离的定义和图3，般侧面和全开角侧面可用底边集ebi来表示其位置，全闭角侧面和内陷面可用顶边集eti来表示其位置，开闭角混合侧面需同时用底边集ebi和顶边集etii来表示其位置。

③边集离散

由于样条曲线的距离计算复杂，为了简化算法，将lp中所有非圆弧曲线均按照离散精度ε离散成直线链形式。通过离散得到的直线段需保证与其他曲线的相对位置关系保持不变。ε太小会降低算法效率，太大会降低精度。为了保证离散后的直线链在一定程度上保持离散前的形状，一般ε的取值范围为ε＜rmin/2.0且ε＜lmin/2.0。式中，rmin、lmin分别为被离散曲线的最小曲率半径和最小曲线长度。

2)线线之间的距离计算

(1)有效性判断

规则1(凸边规则)对于任意边ei，若ei为凸边，则无需计算ei和其他边之间的距离。

规则2(相邻规则)给定槽fp，相邻侧面之间的距离勿需计算。

规则3(垂直规则)对于任意待求距离的两条直边ei与ej，若满足ei⊥ej，则ei与ej之间的距离勿需计算。

规则4(侧位规则)对于任意待求距离的两条边ei、ej，v1代表ei环l在ei起始点的正向矢量，v2代表由ei始点到ej始点的直线矢量。定义向量vz(x,y,z)，令vz＝v1×v2，若满足z≤0，则勿需计算ei与ej之间的距离。

规则5(锐角规则)给定任意环l，ei与ej表示l上待求距离的两条直边，v1与v2分别代表环l在ei与ej始点处正向矢量，若v1·v2>0，则勿需计算ei与ej之间的距离。

规则6(凸弧规则)给定任意环l，沿其正方向，若环上存在凸弧ce，且ce的半径r<转角允许的最大半径rmax，则勿需计算凸弧与该环上其他各边的距离，将凸弧本身的直径作为凸弧到该环任意边的最短距离。

规则7(凹凸性规则)给定任意环l，若存在连续三条边ei-1、ei、ei+1，其中，若ei满足以下两个条件之一：

a.ei的起点与终点凹凸性相反；

b.ei为凸弧；

则ei-1与ei+1之间的距离勿需计算。

规则8(凹弧侧位规则)对于任意待求距离的一条凹弧边cx和一条边ei，a、b为cx的两个端点，o为cx的圆心，c、d为ei的两个端点，定义向量v1(x1,y1,z1),v2(x2,y2,z2),v3(x3,y3,z3),v4(x4,y4,z4)，令若满足以下两个条件之一：

(1)z1>0且z2>0且z3>0且z4>0；

(2)z1<0且z2<0且z3<0且z4<0；

则cx与ei间的距离勿需计算。

规则9(相交规则)对于任意待求距离的两条边ei、ej，点psi与pei分别表示ei的起点与终点，点psj与pej分别代表ej的起点与终点，则分别连接psipsj成直线e1，连接psipej成直线e2，连接peipsj成直线e3，连接peipej成直线e4。若e1，e2，e3，e4与除了ei、ej外的任意一条边存在交点，则无需计算ei与ej之间的距离。

(2)直线段与直线段之间的距离计算

直线段与直线段之间的距离计算可以根据两直线段的相对位置关系不同分为以下两类。如图4(a)所示，从em的始末点向en做垂线段，垂足点为分别为点pa和点pb，从en的始末点向em做垂线段，垂足点为分别为pc和pd，若pa、pb、pc、pd中有一点位于直线段上，则em与en之间的距离必然为某端点所在的垂线段距离；反之，如图4(b)，若pa、pb、pc、pd均不在em与en上，此时em与en之间的距离必然位于两端点之间。

(3)直线段与圆弧之间的距离计算

直线段与圆弧之间的距离计算也可根据圆心到直线段上的垂足位置分为所示两种情况。如图5(a)，圆弧em圆心o到直线en的垂足点p在en上，则垂线段的长度h-r即为所求距离。反之，如图5(b)，若垂足p不在en上，则圆心o与en端点的距离l-r即为所求距离。

(4)圆弧与圆弧之间的距离计算

圆弧与圆弧之间的距离计算情形较为复杂，设圆弧em所在圆心为o1，半径为r1，端点分别为pa、pb，圆弧en所在圆心为o2，半径为r2，端点分别为pc、pd，o1、o2圆心距为d，连接o1o2，交em所在圆于pe，交en所在圆于pf，连接pco1交em所在圆于pg，连接pdo1交em所在圆于ph。根据点pe、pf、pg、pd与圆弧em、e的位置关系n，可以分为如图6所示的7种情况。下面分别讨论这7种情况下圆弧与圆弧之间的距离计算。

a.如图6(a)所示，若pe在em上，pf在en上，则两圆弧之间的距离l＝d-r1-r2。

b.如图6(b)所示，若pe在em上，pf不在en上，pg、ph均在em上，则两圆弧之间的距离l＝min(|pco1|-r1，|pdo1|-r1)。

c.如图6(c)所示，若pe在em上，pf不在en上，pg在em上、ph不在em上，则两圆弧之间的距离l＝|pdo1|-r1。

d.如图6(b)所示，若pe在em上，pf不在en上，pg、ph均不在em上，则两圆弧之间的距离l＝min(|papc|，|papd|，|pbpd|，|pbpd|)。

e.如图6(e)所示，若pe不在em上，pf不在en上，pg、ph均在em上，则两圆弧之间的距离l＝min(|pco1|-r1，|pdo1|-r1)。

f.如图6(f)所示，若pe不在em上，pf不在en上，pg不在em上、ph在em上，则两圆弧之间的距离l＝min(|pco1|-r1，|papc|，|papd|，|pbpd|，|pbpd|)。

g.如图6(g)所示，若pe不在em上，pf不在en上，pg、ph均不在em上，则两圆弧之间的距离l＝min(|papc|，|papd|，|pbpd|，|pbpd|)。