路网上的弹性聚合最近邻查询E-max方法与流程

本发明属于计算机领域，具体涉及空间数据库的查询方法，尤其涉及一种路网上的弹性聚合最近邻查询e-max(精确解-最大值)方法。

背景技术

聚合最近邻查询(aggregatenearestneighbor，以下简称ann)是空间数据库中的经典查询，有广阔的应用场景，比如基于位置服务等。给定一组查询点集合q，ann在数据点集合v中寻找一个点，使得该点到q中所有点的聚合距离最小。这个聚合函数一般是max或者sum。ann问题已经在欧式空间[参见d.papadias,q.shen,y.tao,andk.mouratidis,“groupnearestneighborqueries,”indataengineering,2004.proceedings.20thinternationalconferenceon.ieee,2004,pp.301–312.]和路网上[参见d.papadias,q.shen,y.tao,andk.mouratidis,“groupnearestneighborqueries,”indataengineering,2004.proceedings.20thinternationalconferenceon.ieee,2004,pp.301–312.]得到研究。

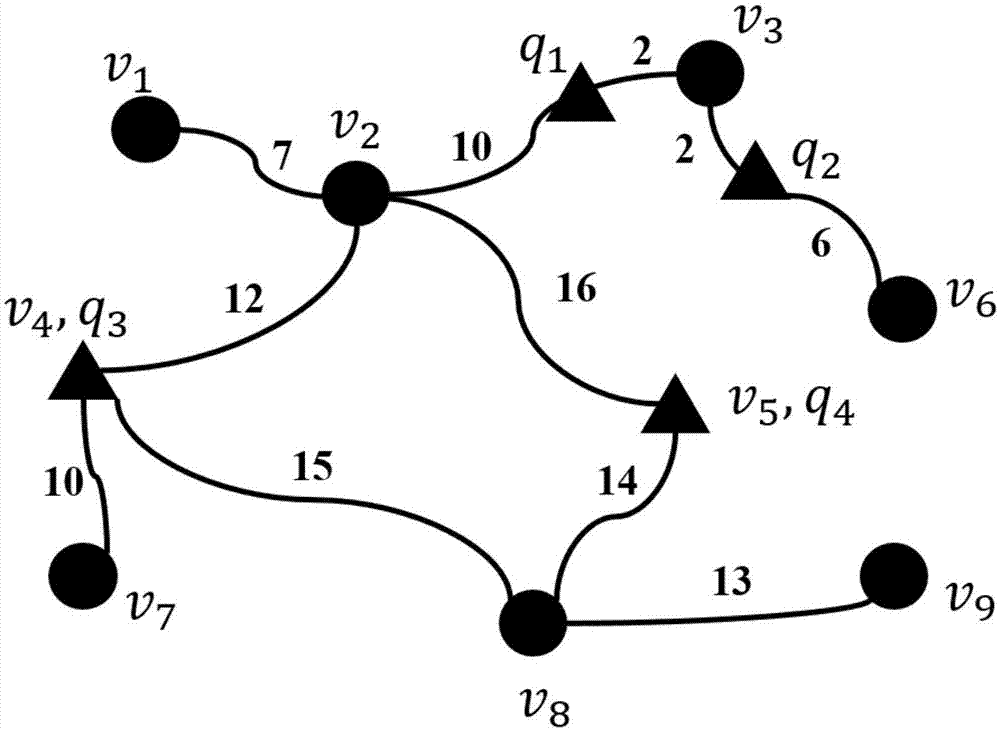
在很多时候，考虑q中的部分查询点则更有意义。考虑图1中的例子，数据点集合是v＝{v1,v2,…,v8,v9,}(圆形)，查询点集合是q＝{q1,q2,q3,q4}(三角形)。注意v3和q3,v5和q4分别共享同一个位置；q1位于(v2,v3)上，q2位于(v3,v6)上。假设v是建造港口的候选位置，q是小型货运集散中心，且每个集散中心每天能存储1吨货物。现在v中寻找一个候选点，收集q所有货物，并使得聚合距离最小。这时max-ann的结果就是v2，距离为16；sum-ann的结果也是v2，距离为52。因为v2相对是q的“中心”，所以我们可以直观地理解这个结果。但是，如果港口每天仅需要2吨货物，即仅需要考虑50％的小型货物集散中心，而不是考虑q中所有查询点。更准确地说，更一般的查询是允许用户指定一个参数目标是在v中寻找一个点，使得该点到q中某个点的聚合距离最小，我们把这种查询称为弹性聚合最近邻查询(flexibleaggregatenearestneighbor，以下简称fann)。如果我们令则max-fann的结果是v3，距离为2；sum-fann的结果也是v3，距离为4。

本发明研究路网上的fann问题。fann查询最早是在欧式空间中提出[参见y.li,f.li,k.yi,b.yao,andm.wang,“flexibleaggregatesimilaritysearch,”inproceedingsofthe2011acmsigmodinternationalconferenceonmanagementofdata.acm,2011,pp.1009–1020.]。相比与欧式空间，路网上的很多操作都更复杂。比如在欧式空间中确定两点间的最短距离可以在常数时间内确定，而在路网中该操作取决于最短路算法。为了在路网中提出更高效的fann算法，有必要利用路网的拓扑结构，从而对不可能的候选点进行剪枝。

据了解，目前没有其他在路网上关于fann的研究工作。我们对fann的研究并不是路网上ann[参见d.papadias,q.shen,y.tao,andk.mouratidis,“groupnearestneighborqueries,”indataengineering,2004.proceedings.20thinternationalconferenceon.ieee,2004,pp.301–312.]的简单扩展。[d.papadias,q.shen,y.tao,andk.mouratidis,“groupnearestneighborqueries,”indataengineering,2004.proceedings.20thinternationalconferenceon.ieee,2004,pp.301–312.]中的ier算法依赖r树，但r树在路网上表现并不好。[d.yan,z.zhao,andw.ng,“efficientalgorithmsforfindingoptimalmeetingpointonroadnetworks,”proceedingsofthevldbendowment,vol.4,no.11,2011.]使用了凸包的方法来对不可能的点进行剪枝，但其可扩展性不好。[m.safar,“groupk-nearestneighborsqueriesinspatialnetworkdatabases,”journalofgeographicalsystems,vol.10,no.4,pp.407–416,2008.][l.zhu,y.jing,w.sun,d.mao,andp.liu,“voronoi-basedaggregatenearestneighborqueryprocessinginroadnetworks,”inproceedingsofthe18thsigspatialinternationalconferenceonadvancesingeographicinformationsystems.acm,2010,pp.518–521.]均使用voronoi图对路网进行分区，但他们常导致划分的不均衡，从而导致效率不高。此外，由于新加入的参数fann的结果会更难找到。q中的任意点均能成为目标，其规模可达

因此，亟需研发一种能解决路网上的fann问题的方法。

技术实现要素：

本发明要解决的技术问题在于提供一种路网上的弹性聚合最近邻查询e-max(精确解-最大值)方法，该方法能大大较少减少了的调用次数，从而提升查询速度，降低成本。

为解决上述技术问题，本发明采用如下技术方案：

本发明提供一种路网上的弹性聚合最近邻查询e-max方法，包括如下步骤：

第一步，定义和初始化：

定义路网g＝(v,e,w)，其中v表示顶点，e表示边，w表示边的权重，δ(vi，vj)表示vi到vj的路网距离；q是查询集合，大小为m；fann查询定义为：一个fann查询是一个五元组返回一个三元组使得：

其中p*是v中使得弹性聚合距离最小的点，是q的最优的弹性子集，r^*就是此时的弹性聚合距离；

定义为弹性聚合函数，它接受一个属于v的点p，一个v的子集q作为输入，返回一个对作为结果，满足：

其中是q的一个子集且

初始化：将r*初始化为无穷大；v中所有的点均未被访问；初始化队列列表(l1,l2,…,lm)，即对于q中的每个点qi，分别生成一个优先级队列，每个队列均包含v中的所有点；为v中每个点加一个计数器，计数器初始为0；

第二步，从上述队列列表的每个队列中取出第一个元素的距离，得到一个序列(d1,d2,…,dm)；

第三步，取得第二步序列(d1,d2,…,dm)中的最小元素对应的v中点的v，并为v的计数器加1；

第四步，判断v的计数器大小，如果计数器大于等于则v就是p*，运行就是最终解，结束算法；否则把v从其所在队列l中出队，进入第二步。

作为本发明优选的技术方案，第一步中，所述生成一个优先级队列是按与qi距离的升序排列。

作为本发明优选的技术方案，第一步中，所述优先级队列内的元素是一个二元组<v,d>，其中v表示v中点，d表示v到qi的距离。

作为本发明优选的技术方案，第四步中，如果计数器小于此时队列不会为空，所述把v从其所在队列l中出队操作是安全的。

与现有技术相比，本发明具有以下有益效果：

1、本发明方法只需要一次计算，算法实现简单，且当q相对集中时，算法效率高。

2、因为只需要使用一次，本发明算法在没有复杂路网索引下也能高效工作。

附图说明

下面结合附图和实施例对本发明进一步说明。

图1是fann的实例示意图。

图2是本发明中sum-fann反例示意图。

图3是本发明路网上的弹性聚合最近邻查询e-max方法的流程图。

图4是本发明算法与baseline基本算法的变化a的效率比较结果示意图。

图5是本发明算法与baseline基本算法的变化m的效率比较结果示意图。

图6是本发明算法与baseline基本算法的变化的效率比较结果示意图。

具体实施方式

现在结合附图对本发明作进一步详细的说明。这些附图均为简化的示意图，仅以示意方式说明本发明的基本结构，因此其仅显示与本发明有关的构成。

1问题定义

路网可以表示为一个无向有权重的图，g(v,e,w)，其中v是顶点集合，e是边的集合，w是e到正实数的映射，表示边的权重。令δ为定义在g上的距离函数，δ(vi，vj)表示vi到vj的路网距离。值得注意的是，边的权重不一定等于两点间的欧式距离。比如，它可以是经过该边需要的时间。显然，如果边的权重和欧式距离成比例，转化就很简单。我们采用类似于[m.l.yiu,n.mamoulis,andd.papadias,“aggregatenearestneighborqueriesinroadnetworks,”ieeetransactionsonknowledgeanddataengineering,vol.17,no.6,pp.820–833,2005.]的方法(归一化)来处理任意的权重。首先，我们计算一个比例系数：

，其中d^ε(vi，vj)表示vi到vj的欧式距离。然后我们将所有权重乘以上面的比例系数。这样，欧式距离依然是其下界。

我们使用q表示查询点集合(queryobjects)，大小为m。表示弹性参数，其中|v|＝n，|q|＝m，在(0,1)之间。为了便于描述，我们假设所有的查询点均在图的顶点，即令g表示一个聚合函数，它定义在一个点p和一个点集p上，在本发明中它是max：

g(p，p)＝max(δ(p，v1)，δ(p，v2)，...，δ(p，vk))，

其中|p|＝k，vi属于p。

这样，我们就可以定义弹性聚合函数它接受一个属于v的点p，一个v的子集q作为输入，返回一个对作为结果，满足：

其中是q的一个子集且

我们的目标是在v中找到一个点p^*使得r^p最小。一个fann查询可以正式定义为：一个fann查询是一个五元组返回一个三元组使得：

其中p^*是v中使得弹性聚合距离最小的点，是q的最优的弹性子集，r^*就是此时的弹性聚合距离。

给定g，q和参数目标是在v中寻找一个点，使得该点到q中某个点的聚合距离(一般是sum或者max)最小。

2.暴力方法

首先，我们先讨论的实现。给定一个p和q，我们至多有多个选择来确定然而，没有必要去考虑每种可能。回顾dijkstra算法(dijkstra算法，是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止)的执行过程：在它的每次扩展步骤，它选择到起点最近的未访问过的点，并更新该点的邻居到起点的距离。这个过程也可以应用在首先，令p为起点，调用dijkstra算法，直到q中有个点被标记为访问过。此时这些被标记的点就是其聚合距离就是r^p。不难发现，我们也可以把看成是关于p和q的knn查询，其中

根据上述fann的定义，我们可以设计fann的暴力解法：我们对每个v中的p均运行算法。过程中，我们维护一个最小的r^p即可。值得一提的是，我们可以利用该r^p或者利用欧式距离作为下界来实现提前介绍一轮迭代。类似的策略对任何使用的算法都有效。

现在我们考虑暴力方法的时间复杂度。因为和dijkstra有相同的复杂度，即o(|e|+nlgn)(假设使用的最小堆为fibonacci堆)，其中|e|是路网中边的数目。因此，总时间为o(n|e|+n²lgn)。

直观上，我们有两种方法来优化该暴力算法：一是尽可能对v中的点进行剪枝(即减少的调用次数)，二是提高的效率。本文下面的内容将着重讨论这两种方法。

3.e-max算法

我们从q开始扩展可以得到很好的性能。算法过程和list算法类似：我们对v中每个点维护一个计算器。每次迭代中，我们在list中取得最小距离的点(第4行)，计算器自增1(表示被一个查询点访问过)(第5行)；如果某个点的计算器达到个，则该点即r*，此时我们可以安全地停止算法(第6-8行)。

算法e-max算法

类似地，在实际地实现中我们没有必要维护m个list，而是把q中的查询点作为起点，并行独立地执行dijkstra算法。值得注意的是，上述方法不能来回答sum-fann问题。图2演示了一个反例。查询点集合q是{q1,q2,q3,q4,q5}，我们按照上述算法的思路，我们会依次访问{…,(q2,<2,v1>),(q1,<4,v2>),(q2,<10,v2>)}，这样p^*就是v2，r^*＝4+10＝15，然而，实际的结果是p^*就是v1，r^*＝2+11＝13，

如图3所示，本发明路网上的弹性聚合最近邻查询e-max方法，包括如下步骤：

第一步，定义和初始化：

定义路网g＝(v,e,w)，其中v表示顶点，e表示边，w表示边的权重，δ(vi，vj)表示vi到vj的路网距离；q是查询集合，大小为m；fann查询定义为：一个fann查询是一个五元组返回一个三元组使得：

其中p^*是v中使得弹性聚合距离最小的点，是q的最优的弹性子集，r^*就是此时的弹性聚合距离；

定义为弹性聚合函数，它接受一个属于v的点p，一个v的子集q作为输入，返回一个对作为结果，满足：

其中是q的一个子集且

初始化：将r^*初始化为无穷大；v中所有的点均未被访问；初始化队列列表(l1,l2,…,lm)，即对于q中的每个点qi，分别生成一个优先级队列，每个队列均包含v中的所有点；为v中每个点加一个计数器，计数器初始为0；

第二步，从上述队列列表的每个队列中取出第一个元素的距离，得到一个序列(d1,d2,…,dm)；

第三步，取得第二步序列(d1,d2,…,dm)中的最小元素对应的v中点的v，并为v的计数器加1；

第四步，判断v的计数器大小，如果计数器大于等于则v就是p^*，运行就是最终解，结束算法；否则把v从其所在队列l中出队，进入第二步。

优势：本发明方法只需要一次计算，算法实现简单，且当q相对集中时，算法效率高。因为只需要使用一次，本发明算法在没有复杂路网索引下也能高效工作。

4实验

4.1设置

我们使用标准c++实现了上面的算法，并在一台linux机器上运行实验，机器的配置是64位intelxeon3.30ghzcpu，16gbram。我们使用一个1m大小的lru缓存。所有的路网数据均来自真实世界。如下表所示：

对于路网中的fann问题，有很多影响开销的因素。在我们的实验中，我们主要关注3个最主要的：

●a,q的覆盖率

●m，q的大小

●弹性参数

我们逐个变化这三个变量。当改变其中一个时，其他两个保持不变。a，m和的默认值分别是0.6,60，0.6。出于篇幅限制，除了在衡量可扩展性时展示了sf,lks,ctr和usa数据集，我们默认仅展示sf数据集的结果。此外在5.4部分我们研究了g树在不同数据集上(相对)最优参数，默认选择b＝6,t＝200(sf)，t＝300(lks)，t＝400(ctr)和t＝500(usa)。4.2效率

首先，我们考察本发明算法与baseline基本算法的效率比较结果示意图。baseline基本算法指：遍历v中的路网点，然后运行基于dijkstra算法的

变化a：我们使用0.1,0.2,0.4,0.6,0.8和1.0来变化a。结果见图4。

变化m：我们使用10,20,30,40,60,80,100来变化m。结果见图5。

变化我们使用0.1,0.2,0.4,0.6,0.8,1.0变化结果见图6。

以上述依据本发明的理想实施例为启示，通过上述的说明内容，相关工作人员完全可以在不偏离本项发明技术思想的范围内，进行多样的变更以及修改。本项发明的技术性范围并不局限于说明书上的内容，必须要根据权利要求范围来确定其技术性范围。