一种基于马尔可夫链蒙特卡洛的Bayesian动态预测方法与流程

本发明属于计算机技术领域，具体涉及一种基于马尔可夫链蒙特卡洛的bayesian动态预测方法。

背景技术：

贝叶斯决策的主要工具是经典贝叶斯方法，其理论基础是贝叶斯定理。贝叶斯定理是由英国数学家贝叶斯创立的一种用所观察到数据对相关概率的主观判断进行修正的方法。传统统计推断技术没有综合运用已有的信息，使得分析结论的可信度相对降低，通过贝叶斯方法可以将人们的主观认识和经验数据相结合，得到更可靠的推断结果。贝叶斯理论中，贝叶斯推断和分析可以通过利用贝叶斯公式计算后验分布来实现，但利用联合概率分布进行概率推理的复杂程度相对于高维变量个数呈指数级增长。在实际计算过程中，后验分布往往是高维、复杂且不常见的分布形式，这种分布形式的积分计算过程复杂，甚至无解。

马尔可夫链蒙特卡洛方法(mcmc方法)是基于贝叶斯理论，通过计算机实现蒙特卡洛模拟计算积分的方法。解决了贝叶斯后验分布的高维复杂积分问题，开拓了贝叶斯推断的应用领域。目前，基于mcmc方法的贝叶斯生存分析方法已经在各个学科广泛应用，该方法将马尔可夫过程引入蒙特卡洛模拟中，弥补了蒙特卡洛积分只能进行静态模拟的弊端，实现了抽样分布随着模拟的进行而改变的动态模拟。在工程结构可靠性研究的应用中也很好的解决了贝叶斯实际建模计算问题，提高了模型的有效性和可操作性。

工程结构可靠性的研究通常是通过考虑影响结构性能退化的各不确定因素，推算结构抗力的时变概率特性，从而建立结构抗力随机过程模型。但在具体的实践中，因结构耐久性问题的时间周期长、影响因素复杂、不确定性大、不同结构从材料到构件再到结构设计的差异性等因素，很难用某一种模型来概括。已有的工程结构失效预测和可靠性评估模型也无法做到充分考虑实际工程中各种复杂因素对各参数的影响。因此研究结构可靠性就要求建立合理的结构性能随机过程模型。

以上大部分研究仅是针对设计方案中的可靠性，并不包含真实结构的可靠性。在实际工程结构问题当中，为了确保结构系统安全，研究其性能和可靠性退化过程，常常要对结构系统进行健康监测，用无损检测方法量测数据，但这些数据具有很大的不确定性，因此基于量测数据的结构时变可靠性评估相对而言更合理。本发明基于贝叶斯更新理论，充分耦合服役工程结构性能退化过程(模型的不确定性)和量测数据、提出不断动态更新的有效预测方法。

技术实现要素：

为了克服上述现有技术存在的不足，本发明提供了一种基于马尔可夫链蒙特卡洛的bayesian动态预测方法。

为了实现上述目的，本发明提供如下技术方案：

一种基于马尔可夫链蒙特卡洛的bayesian动态预测方法，包括以下步骤：

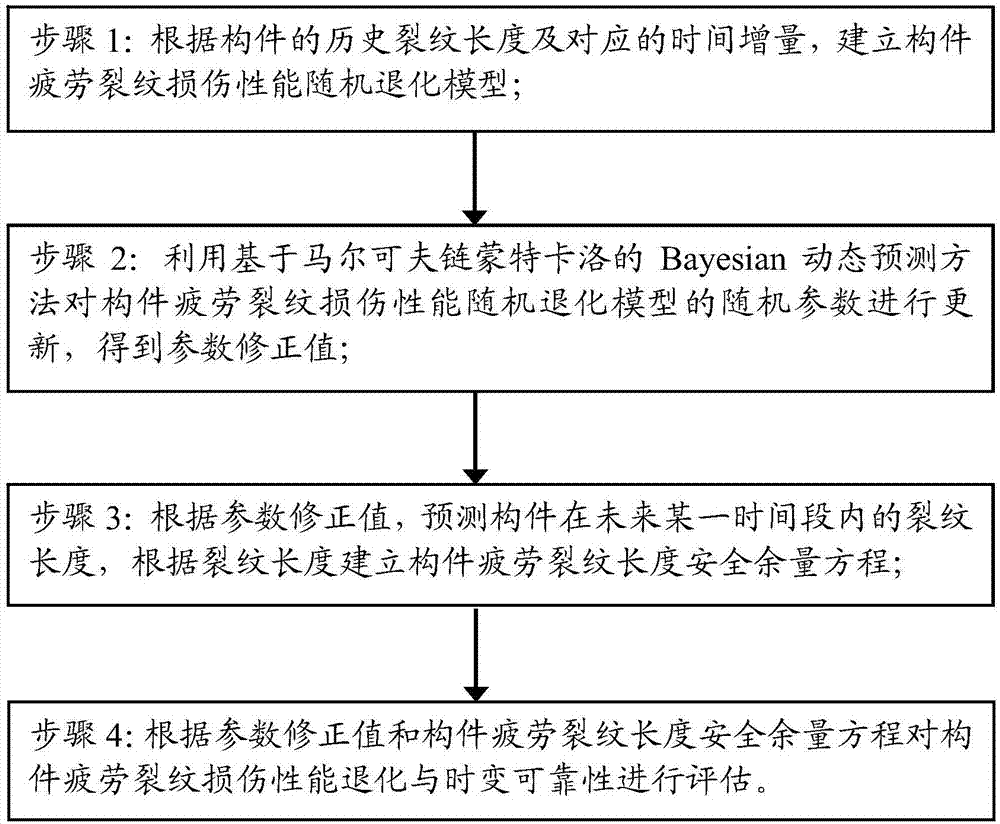
步骤1：根据构件的历史裂纹长度及对应的时间增量，建立构件疲劳裂纹损伤性能随机退化模型；

步骤2：利用基于马尔可夫链蒙特卡洛的bayesian动态预测方法对构件疲劳裂纹损伤性能随机退化模型的随机参数进行更新，得到参数修正值；

步骤3：：根据参数修正值，预测构件在未来某一时间段内的裂纹长度，根据裂纹长度建立构件疲劳裂纹长度安全余量方程；

步骤4：根据参数修正值和构件疲劳裂纹长度安全余量方程对构件疲劳裂纹损伤性能退化与时变可靠性进行评估。

优选地，所述步骤1具体包括：

步骤1.1：建立构件疲劳裂纹扩展确定性模型

对于一个含有表面裂纹a的工程结构构件，依据线弹性断裂力学理论，裂纹端部应力强度因子k在某一应力水平作用下应力σ可以表示成如下形式：

式(1)中：y表示应力强度修正系数，反映了构件和裂纹的几何形状；a为半裂纹长度；在构件承受静荷载时，只有其应力水平达到临界应力σc时，即裂纹端部的应力强度因子达到临界值kc时，才会立即发生失稳断裂，此时相对应的临界裂纹长度为ac；当静应力水平降低到σ0，σ0<σc，则构件不会发生失稳破坏；但如果构件承受一个与静应力σ0大小相等的往复循环应力，则初始裂纹a0在循环应力σ0作用下发生缓慢扩展，根据著名的pari半经验公式，疲劳裂纹扩展速率可以写成以下形式：

其中da/dn表示裂纹扩展速率；n为荷载循环次数；δk表示应力强度因子变化幅度，由式(1)有：假设疲劳裂纹扩展过程中，δσ和y保持不变，则可取δk(a)＝a，由积分公式(2)得

其中a(0)是n＝0时构件的初始疲劳裂纹长度，a(n)表示荷载循环次数为n时的裂纹长度；c、m为材料参数，通常为试验所得；

步骤1.2：建立构件疲劳裂纹损伤性能退化概率模型

令式(3)中材料参数c＝θ1、m-1＝θ2，并假设这些参数均为不确定性参数，则对式(3)两边取自然对数，并令y＝ln(a(n)/a(0))，有

其中yij表示第i(i＝1,2,…,n)个疲劳裂纹在荷载循环到tj(j＝1,2,…,m)＝n时对应的相对疲劳裂纹扩展长度，工程结构构件相应性能退化；tj是时间变量，表示作用在构件上的疲劳荷载循环次数，为性能变量的观测时间；η(·)是描述性能变量变化的轨迹函数，它是t的单调非线性函数，在许多情况下它也是参数θ(θ1i,θ2i)的非线性函数；是性能退化函数η(·)中的未知随机参数向量，q是参数向量位数，θ是参数向量的取值空间；εij是反映性能退化过程中第i个疲劳裂纹在tj时刻相对扩展长度的不确定性的误差项；

假设(1)对应特定的tj，随机误差项序列εij，i＝1,2,…,n独立同分布，也就是说，εij在空间上是独立的；(2)对于特定的疲劳裂纹i，随机误差项序列εij，j＝1,2,…,m是相关的；(3)随机误差项序列εij服从均值为0，未知协方差矩阵为σε的多维随机变量正态分布，即n(0,σε)；

定义yi＝(yi1,yi2,…,yim)^t和ηi＝(ηi1,ηi2,…,ηim)^t，其中t表示矩阵转置；用fmvn(x/μ,σ)表示均值为μ，协方差为σ的多维随机变量正态分布概率密度函数，因此，在给定ηi的情况下，由式(3)有：

式中σε表示随机误差项m×m阶的协方差方阵，其中矩阵元素等于ρklσkσl，(k＝1,2,…,m；l＝1,2,…,m)；|σε|为协方差方阵行列式值；ρkl为荷载循环次数k次和l次时随机误差项之间的相关系数，σk和σl分别表示荷载循环次数k次和l次时随机误差项的标准方差。

优选地，所述步骤2具体包括：

步骤2.1：先验分布

假定式(4)中随机误差项εij独立同分布，则有ρkl＝0，σε变为对角线元素为未知常数的m×m阶协方差矩阵；对于特定的疲劳裂纹i，公式(4)共有(θ,σε)两类参数，它们的联合先验分布函数为π(θ,σε)；随机参数θ与σε之间是彼此独立的，它们的联合先验分布可以写成：π(θ,σε)＝π(θ)π(σε)＝π(θi1)π(θi2)π(σε)，其中π(θi1)、π(θi2)和π(σε)分别是按照各自方式构造的关于θi1、θi2和σε的先验分布密度函数；采用无信息先验分布σε>0；

步骤2.2：性能退化过程似然函数和后验分布

对于特定的疲劳裂纹i，假定在tj(j＝1,2,…,m)时刻有损伤性能退化量测值yi1,yi2,…,yim；由于随机误差项序列εij，j＝1,2,…,m是独立同分布的随机变量，在给定θ和σε的条件下，性能退化样本yi1:m的条件联合分布函数或似然函数为：

在已知联合先验分布π(θ,σε)的基础上，得到性能退化量测值d(＝yi1,yi2,…,yim)后利用bayes更新公式来推断后验分布p(θ,σε|d)，即有:

其中θ、ω分别是θ、σε的取值空间；令π(θ1ι)π(θ2ι)π(σε)＝π(θ1,θ2,θ3)，从给定初始样本开始，则根据全条件分布gibbs抽样技术，样本生成如下：

θ1⁽¹⁾从全条件分布π(θ1⁽⁰⁾)π(θ2⁽⁰⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽⁰⁾,θ2⁽⁰⁾,θ3⁽⁰⁾)产生；

θ2⁽¹⁾从全条件分布π(θ1⁽¹⁾)π(θ2⁽⁰⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽¹⁾,θ2⁽⁰⁾,θ3⁽⁰⁾)产生；

θ3⁽¹⁾从全条件分布π(θ1⁽¹⁾)π(θ2⁽¹⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽¹⁾,θ2⁽¹⁾,θ3⁽⁰⁾)产生；

以上gibbs抽样技术的关键在于仅考虑了单变量的条件分布；抽样样本可以通过选择一个建议分布来生成，选择随机游走链作为建议分布：

使用这种分布进行数值模拟简单，而且其接受概率也仅取决于后验分布；m-h算法就是通过以上gibbs抽样技术得到样本并利用接受概率决定是否接受还是拒绝即：接受概率的表达形式如下：

重复上述迭代过程直到各分量θk+1的遍历均值稳定后，可生成一系列所需要采集的样本{θ1,θ2,θ3,…}，利用这些后验样本，估计后验分布和随机参数的置信区间，得到参数修正值。

优选地，所述步骤3具体包括：

建立构件单根疲劳裂纹长度安全余量方程，作为进行可靠性分析的极限状态方程：

z＝acr-y(tk+δt)≥0(10)

式中：z为疲劳裂纹长度的安全余量；acr为给定的疲劳裂纹临界值；y(tk+δt)为疲劳裂纹在tk+δt时刻的预测值，y(tk+δt)＝η(tk,θ1,θ2)+εk+1；tk是当前时刻，δt是关心的未来时间区间长度；y(t1),y(t2),…,y(tk)是当前时刻以及过去时刻的疲劳裂纹长度量测数据；εk+1表示疲劳裂纹损伤性能退化轨迹模型在tk+δt的随机误差项，假设它与ε1,ε2,…,εk独立同分布，即：

优选地，所述步骤4具体包括：

疲劳裂纹损伤构件时变可靠性bayes预测

根据极限状态方程(10)，构件在未来某一时刻tk+δt的可靠概率计算公式可以表示如下：

其中g(θ1,θ2,σε,tk,δt,acr)＝z＝acr-y(tk+δt)，服从n(0,σε)分布；

在获得未知随机参数和随机误差项的后验分布后，将式(11)的求解转化为如下后验期望值：

每次达到疲劳试验的设计试验节点，收集到一个新的量测数据，利用收集到的历史量测数据，相应地更新似然函数，利用式(12)计算未来一段时间δt内疲劳裂纹损伤构件的可靠性分析和预测，并绘制一条时变可靠度变化曲线。

本发明提供的基于马尔可夫链蒙特卡洛的bayesian动态预测方法利用马尔可夫链蒙特卡洛(markovchainmontecarlo，简称mcmc)方法，直接从后验分布函数中抽样而无需解析求积分来进行bayes更新分析，从而建立基于贝叶斯更新理论，充分耦合服役工程结构性能退化过程(模型的不确定性)和量测数据、提出不断动态更新的有效预测方法；结合土木工程结构的特点和近年来结构可靠性的研究方向，不再只追求通用性的退化模型，利用信息的更新考虑检测维修策略，从静态的时不变思维转向动态的时变思维，具体为：

1)基于马尔卡夫链蒙特卡洛方法对构件退化损伤模型参数进行修正，充分考虑了模型参数的先验信息，降低了抽样过程中不确定因素对抽样结果的影响；

2)基于贝叶斯理论的信息更新，将结构的时变可靠性问题由静态思维转向为动态思维，综合已经发生的历史检测信息，减小主观不确定性；

3)算例结果表明，实时可靠性预测方法能有效预测产品失效事件的发生，从而可以为预测维修策略的制定提供相应的依据。

附图说明

图1为本发明实施例1的基于马尔可夫链蒙特卡洛的bayesian动态预测方法的流程图；

图2(a)为t∈(0.10,0.11]时间内疲劳裂纹损伤性能退化构件时变可靠度预测曲线；

图2(b)为t∈(0.11,0.12]时间内构件时变可靠度预测曲线的变化趋势；

图3为t∈(0.10,0.12]时间内疲劳裂纹损伤性能退化轨迹预测曲线；

图4为t∈(0.05,0.12]时间内疲劳裂纹损伤性能退化轨迹预测曲线。

具体实施方式

下面结合附图，对本发明的具体实施方式作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

实施例1

首先，本实施例对bayes更新定理进行一定的说明：

bayes更新定理是概率统计中的应用所观察到的现象对有关概率分布的主观判断(即先验概率)进行修正的标准方法。bayes更新公式是关于随机事件a和b的条件概率和边缘概率的。它可以表述为：在样本空间ω中有a1,…,an为相互独立且完备的随机事件组，即：aiaj＝φ,p(ai)>0；另外，有一事件b也定义在样本空间ω中，即：b∈ω，且随机事件b一定与随机事件ai的一个或多个有交集；a∪b＝ω。如果随机事件b发生，则随机事件ai发生的概率为：

其中pr(ai)是ai的先验概率或边缘概率。之所以称为“先验”是因为它在随机事件b出现前的概率；pr(ai/b)是在经过获得新观测信息，即随机事件b发生后随机事件ai发生的概率(条件概率)，也由于得自b的取值而被称作ai的后验概率，后验概率依赖于得到的新观测信息；pr(b/ai)是在随机事件ai发生后随机事件b(新观测信息)发生的条件概率，也由于得自ai的取值而被称作b的似然度。bayes公式中分子为条件概率pr(b/ai)与pr(ai)之积是随机事件ai和随机事件b同时发生的条件联合概率；分母为条件联合概率中新观测信息b的全概率是常量，也作标准化常量。

依据上面说明，bayes更新公式可用文字表述为：更新概率(后验概率)＝新观测信息的条件概率(似然度×先验概率)/新观测信息的全概率(标准化常量)，也就是说，后验概率与先验概率和似然度的乘积成正比。另外，比例pr(b/ai)/pr(b)有时也被称作标准似然度，因此，bayes更新公式可进一步用文字表述为：后验概率＝标准似然度×先验概率。

需要指出的是，当随机变量ai为连续型时，则式(1)分母中的新观测信息的全概率改写为pr(b)＝∫ap(b/a)p(a)da。这个积分通常是高维积分，很复杂，一般情况下很难有解析解，而必须求助于数值解。

根据上述bayes更新定理，本实施例提供了一种基于马尔可夫链蒙特卡洛的bayesian动态预测方法，具体如图1所示，包括以下步骤：

步骤1：根据构件的历史裂纹长度及对应的时间增量，建立构件疲劳裂纹损伤性能随机退化模型，具体包括：

步骤1.1：建立构件疲劳裂纹扩展确定性模型

对于一个含有表面裂纹a的工程结构构件，依据线弹性断裂力学(lefm)理论，裂纹端部应力强度因子k在某一应力水平作用下应力σ可以表示成如下形式：

式中y表示应力强度修正系数，反映了构件和裂纹的几何形状；a为半裂纹长度。在构件承受静荷载(一般使用环境)时，只有其应力水平达到临界应力σc时，即裂纹端部的应力强度因子达到临界值kc时，才会立即发生失稳断裂，此时相对应的临界裂纹长度为ac。当静应力水平降低到σ0(σ0<σc)，则构件不会发生失稳破坏，但如果构件承受一个与静应力σ0大小相等的往复循环应力，则初始裂纹a0在循环应力σ0作用下发生缓慢扩展；根据著名的paris半经验公式，疲劳裂纹扩展速率可以写成以下形式：

其中da/dn表示裂纹扩展速率；n为荷载循环次数；δk表示应力强度因子变化幅度，由式(2)有：假设疲劳裂纹扩展过程中，δσ和y保持不变，则可取δk(a)＝a，由积分公式(3)得

其中a(0)是n＝0时构件的初始疲劳裂纹长度，a(n)表示荷载循环次数为n时的裂纹长度，c、m为材料参数，通常为试验所得。

步骤1.2：建立构件疲劳裂纹损伤性能退化概率模型

令式(4)中材料参数c＝θ1、m-1＝θ2，并假设这些参数均为不确定性参数，则对式(4)两边取自然对数，并令y＝ln(a(n)/a(0))，有

其中yij表示第i(i＝1,2,…,n)个疲劳裂纹在荷载循环到tj(j＝1,2,…,m)＝n时对应的相对疲劳裂纹扩展长度，工程结构构件相应性能退化；tj是时间变量，表示作用在构件上的疲劳荷载循环次数，为性能变量的观测时间。η(·)是描述性能变量变化的轨迹函数，它是t的单调非线性函数，在许多情况下它也是参数θ(θ1i,θ2i)的非线性函数；是性能退化函数η(·)中的未知随机参数向量，q是参数向量位数，θ是参数向量的取值空间。参数向量的“随机性”应该理解为，对于同一轨迹的性能退化，模型参数的取值是确定的；对于不同轨迹的性能退化，模型参数的取值是随机的，这种随机性可以由某个概率分布刻画。εij是反映性能退化过程中第i个疲劳裂纹在tj时刻相对扩展长度的不确定性的误差项。为此，进一步假设(1)对应特定的tj，随机误差项序列εij，i＝1,2,…,n独立同分布，也就是说，εij在空间上是独立的；(2)对于特定的疲劳裂纹i，随机误差项序列εij，j＝1,2,…,m是相关的；(3)随机误差项序列εij服从均值为0，未知协方差矩阵为σε的多维随机变量正态分布，即n(0,σε)。

定义yi＝(yi1,yi2,…,yim)^t和ηi＝(ηi1,ηi2,…,ηim)^t，其中t表示矩阵转置；用fmvn(x/μ,σ)表示均值为μ，协方差为σ的多维随机变量正态分布概率密度函数，因此，在给定ηi的情况下，由式(4)有：

式中σε表示随机误差项m×m阶的协方差方阵，其中矩阵元素等于ρklσkσl，(k＝1,2,…,m；l＝1,2,…,m)；|σε|为协方差方阵行列式值。ρkl为荷载循环次数k次和l次时随机误差项之间的相关系数，σk和σl分别表示荷载循环次数k次和l次时随机误差项的标准方差。

步骤2：利用基于马尔可夫链蒙特卡洛的bayesian动态预测方法对构件疲劳裂纹损伤性能随机退化模型的随机参数进行更新，得到参数修正值，具体包括：

步骤2.1：先验分布

假定式(5)中随机误差项εij独立同分布，则有ρkl＝0，σε变为对角线元素为未知常数的m×m阶协方差矩阵。因此，对于特定的疲劳裂纹i，公式(5)共有(θ,σε)两类参数，它们的联合先验分布函数为π(θ,σε)。关于该联合先验分布的确定可以基于以下两方面事实进行选择：一是未知随机参数θ反映的是构件疲劳裂纹损伤性能退化轨迹发展的不确定性，它可以通过分析其它同类疲劳裂纹损伤性能的退化轨迹发展过程分析得到，或先通过对母体特性进行了解，然后综合一组专家意见或个人判断，做出主观判断得到；二是随机参数σε刻画的是疲劳裂纹损伤性能退化轨迹模型中误差项的数据分散程度(标准差)，而误差项反映了性能退化轨迹模型与性能量测数据之间拟合程度的不确定性。因此，随机参数θ与σε之间是彼此独立的，它们的联合先验分布可以写成：π(θ,σε)＝π(θ)π(σε)＝π(θi1)π(θi2)π(σε)，其中π(θi1)、π(θi2)和π(σε)分别是按照各自方式构造的关于θi1、θi2和σε的先验分布密度函数。需要指出的是，由于在获得实测数据之前，误差项的标准差σε取值信息是无法预先得知的，不能带有任何倾向性的主观假定，因此，σε的先验分布常常采用无信息先验分布。注意到随机参数σε反映的是拟合数据的离散程度，是尺度参数。于是，可以采用无信息先验分布σε>0；

步骤2.2：性能退化过程似然函数和后验分布

对于特定的疲劳裂纹i，假定在tj(j＝1,2,…,m)时刻有损伤性能退化量测值yi1,yi2,…,yim。由于随机误差项序列εij，j＝1,2,…,m是独立同分布的随机变量，在给定θ和σε的条件下，性能退化样本yi1:m的条件联合分布函数或似然函数为：

在已知联合先验分布π(θ,σε)的基础上，得到性能退化量测值d(＝yi1,yi2,…,yim)后就可以利用bayes更新公式(1)来推断后验分布p(θ,σε|d)，即有:

其中θ、ω分别是θ、σε的取值空间。公式(8)中的分母通常很复杂、一般难以用解析法计算其积分，必须求助于数值方法。马尔卡夫链蒙特卡洛(mcmc)抽样技术是一种特别受欢迎的方法，因为不需要求解多重积分，而是直接从后验分布抽样。下面结合mcmc方法中的gibbs抽样技术和m-h算法，建立一种组合抽样技术。为了书写上的便利，令π(θ1ι)π(θ2ι)π(σε)＝π(θ1,θ2,θ3)，从给定初始样本开始，则根据全条件分布gibbs抽样技术，样本生成如下：

θ1⁽¹⁾从全条件分布π(θ1⁽⁰⁾)π(θ2⁽⁰⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽⁰⁾,θ2⁽⁰⁾,θ3⁽⁰⁾)产生；

θ2⁽¹⁾从全条件分布π(θ1⁽¹⁾)π(θ2⁽⁰⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽¹⁾,θ2⁽⁰⁾,θ3⁽⁰⁾)产生；

θ3⁽¹⁾从全条件分布π(θ1⁽¹⁾)π(θ2⁽¹⁾)π(θ3⁽⁰⁾)l(y1:m|θ1⁽¹⁾,θ2⁽¹⁾,θ3⁽⁰⁾)产生；

以上gibbs抽样技术的关键在于仅考虑了单变量的条件分布。抽样样本可以通过选择一个建议分布来生成。这里选择随机游走链作为建议分布：

使用这种分布进行数值模拟简单，而且其接受概率也仅取决于后验分布。m-h算法就是通过以上gibbs抽样技术得到样本θi^(k+1)，并利用接受概率决定是否接受θk+1＝θi^(k+1)，还是拒绝θk+1＝θi^(k+1)，即：θk+1＝θi^(k)，接受概率的表达形式如下：

重复上述迭代过程直到各分量θk+1的遍历均值稳定后，可生成一系列所需要采集的样本{θ1,θ2,θ3,…}。利用这些后验(更新)样本，即可估计后验分布和随机参数的置信区间，得到参数修正值。

步骤3：根据参数修正值，预测构件在未来某一时间段内的裂纹长度，根据裂纹长度建立构件疲劳裂纹长度安全余量方程，具体包括：

建立构件单根疲劳裂纹长度安全余量方程，作为进行可靠性分析的极限状态方程：

z＝acr-y(tk+δt)≥0(11)

式中：z为疲劳裂纹长度的安全余量；acr为给定的疲劳裂纹临界值；y(tk+δt)为疲劳裂纹在tk+δt时刻的预测值，y(tk+δt)＝η(tk,θ1,θ2)+εk+1；tk是当前时刻，δt是未来时间区间长度；y(t1),y(t2),…,y(tk)是当前时刻以及过去时刻的疲劳裂纹长度量测数据。εk+1表示疲劳裂纹损伤性能退化轨迹模型在tk+δt的随机误差项，假设它与ε1,ε2,…,εk独立同分布，即：

步骤4：根据参数修正值和构件疲劳裂纹长度安全余量方程对构件疲劳裂纹损伤性能退化与时变可靠性进行评估，具体包括：

疲劳裂纹损伤构件时变可靠性bayes预测

要了解tk+δt时刻的疲劳裂纹损伤性能退化后的构件可靠性，就必须依据当前时刻以及过去时刻的疲劳裂纹长度量测数据，对其可靠度进行评价。根据极限状态方程(11)，构件在未来某一时刻(tk+δt)的可靠概率计算公式可以表示如下：

其中g(θ1,θ2,σε,tk,δt,acr)＝z＝acr-y(tk+δt)，服从n(0,σε)分布。

一般说来，要解析求解式(12)积分通常很困难，因此，必须使用bayes更新公式(8)和式(9)和(10)所建立的抽样方法，以解决预测和可靠度分析问题。在获得未知随机参数和随机误差项的后验分布后，可将式(12)的求解转化为如下后验期望值：

每次达到疲劳试验的设计试验节点，就会收集到一个新的量测数据。利用收集到的历史量测数据，相应地更新似然函数，即可利用式(13)计算未来一段时间δt(可以取不同值)内疲劳裂纹损伤构件的可靠性分析和预测，并绘制一条时变可靠度变化曲线。

图2(a)为t∈(0.10,0.11]时间内疲劳裂纹损伤性能退化构件时变可靠度预测曲线。如图2(a)所示，t∈(0.10,0.11]时间内构件时变可靠度预测曲线随时间增长，下降非常缓慢，可靠性变化范围在1.0～0.9999之间，这说明构件在t∈(0.10,0.11]内失效的可能性很小。图2(b)给出了t∈(0.11,0.12]时间内构件时变可靠度预测曲线的变化趋势。从图2(b)可以看出，该时变可靠度预测曲线与t∈(0.10,0.11]时间内的时变可靠度预测曲线的变化特征明显不同，下降速度非常快，当t＝0.115左右时变可靠度降为0。如果取时变可靠度下降10％作为构件疲劳失效的阈值，那么从图中曲线可以看出，此时t＝0.1134，对应的可靠度为0.9008，这与实测得到的第9条退化轨迹的疲劳失效时间t＝0.113完全吻合，证实了本文方法的有效性。

选择在疲劳试验终止时，裂纹长度尚未达到临界值的第18条疲劳裂纹损伤性能退化轨迹作为预测疲劳损伤构件的疲劳裂纹增长的研究对象，构建疲劳裂纹增长概率模型随机参数的更新方法，动态预测疲劳裂纹损伤性能退化轨迹。图3为t∈(0.10,0.12]时间内疲劳裂纹损伤性能退化轨迹预测曲线。如图3所示，当t＝0.11时，疲劳裂纹长度为1.2828英寸，实际量测得的疲劳裂纹长度为1.28英寸，绝对误差为0.0028；当t＝0.12时，疲劳裂纹长度为1.3418英寸，实际量测得的疲劳裂纹长度为1.35英寸，绝对误差为0.0082，证实了本实施例提供的方法的准确性。

图4为t∈(0.05,0.12]时间内疲劳裂纹损伤性能退化轨迹预测曲线，其中第1次更新是以t＝0.04时刻的已收集量测数据，相应的更新似然函数后得到的疲劳裂纹性能损伤退化轨迹曲线，第2次更新是以t＝0.05时刻收集到的历史量测数据进行更新得到的退化轨迹曲线。

从图4中可以看出，利用数据更新疲劳裂纹增长概率模型后得到的退化轨迹与实际量测得到的退化轨迹曲线相近，第1次更新后得到的退化轨迹与实际量测得到的退化轨迹的平均绝对误差为0.0159英寸，均方根误差为0.0173，平均绝对百分比误差为1.3175％；第2次更新的退化轨迹更接近实际量测的退化轨迹，其平均绝对误差仅为0.0117英寸，均方根误差为0.0128，平均绝对百分比误差为0.9670％。对比上述三个评价指标可知，第2次更新后得到的预测模型的平均绝对误差、均方根误差以及平均绝对百分比误差均小于第1次更新后得到的预测模型，可靠性更高。同时两次更新后得到的退化轨迹预测图相近，更进一步证实了贝叶斯更新理论在结构疲劳失效预测中的有效性和精确性，由此建立的构件性能退化损伤的贝叶斯动态预测模型更符合实际工程。

本实施例以结构性能退化过程中疲劳裂纹增长模型为例，疲劳裂纹增长会引起结构性能退化，对结构未来性能退化的预测需要结合具体结构的实际监测数据进行更新。本实施例首先依据线弹性断裂力学(lefm)理论和paris半经验疲劳裂纹扩展速率公式，根据构件的历史裂纹长度及对应的时间增量，建立构件疲劳裂纹损伤性能随机退化模型；利用基于马尔可夫链蒙特卡洛的bayesian动态预测方法，结合实际观测数据对构件疲劳裂纹损伤性能随机退化模型的随机参数进行更新，进而实时预测结构在未来一段时间内结构性能退化可靠性和寿命评估。作为一个应用算例，使用本实施例提出的方法结合已有的疲劳裂纹增长试验数据进行了模拟仿真试验，本方法可以有效地预测疲劳裂纹增长模型中随机参数和结构时变可靠性变化规律，达到为土木工程结构中疲劳裂纹损伤结构维修与决策提供科学依据的目的。

以上所述实施例仅为本发明较佳的具体实施方式，本发明的保护范围不限于此，任何熟悉本领域的技术人员在本发明披露的技术范围内，可显而易见地得到的技术方案的简单变化或等效替换，均属于本发明的保护范围。