一种涡轮叶片概率损伤容限分析方法与流程

本发明属于航空发动机结构安全领域，特别涉及到了一种涡轮叶片概率损伤容限分析方法。

背景技术：

涡轮叶片是燃气轮机、航空发动机等的核心部件，其在高温高压高流速的燃气推动作用下高速旋转，涡轮叶片受到强大燃气推力和弯应力作用，反复频繁地起停及变工况运行使得涡轮叶片处于交变的应力环境中而容易发生疲劳断裂，损伤容限分析对保证其安全运行至关重要。叶片在服役环境中，通常受到不确定性因素影响，以确定性断裂力学为基础建立的损伤容限分析很多时候已难以描述真实裂纹结构中的裂纹扩展行为。为了更准确地评估叶片结构剩余强度的可靠度，保证叶片结构的安全，有必要对其进行概率损伤容限分析。然而，实际工程中若采用传统的蒙特卡洛方法对其进行分析，需要进行大量的确定性裂纹扩展分析获取不同裂纹扩展路径下的应力强度因子(sifs)，非常繁琐且不经济。

因此，有必要提出一种仅需少量确定性裂纹扩展分析的疲劳概率损伤容限分析方法，仅根据参数的分布即可对涡轮叶片的疲劳裂纹扩展寿命进行预测。本发明针对叶片裂纹扩展寿命模型的强非线性及各参数间的大不确定性与相关性等问题，提出了一种涡轮叶片概率损伤容限分析方法对其疲劳扩展寿命分布进行预测。

技术实现要素：

针对涡轮叶片裂纹扩展寿命模型的强非线性及各参数间的大不确定性与相关性等问题，本发明提出了一种仅需少量确定性裂纹扩展分析即可预测疲劳裂纹扩展寿命分布的涡轮叶片概率损伤容限分析方法，包括如下步骤：

第一步：涡轮叶片的三维裂纹扩展随机建模，准确预测涡轮叶片的裂纹扩展寿命是航空发动机结构设计中的一个重要问题。本发明采用基于线弹性断裂力学的paris公式来预测疲劳裂纹扩展寿命：

式中，a代表裂纹尺寸，n代表加载次数(裂纹扩展寿命)，c和m是只与材料有关的参数，δk代表一个循环中的应力强度因子幅值。对于i型断裂，δk＝ki；对于复合型断裂，δkeff表示有效应力强度因子，可基于能量释放率或其他准则求解。

当kmax小于断裂韧性kic，δk大于裂纹扩展门槛值δkth时，对式(1)积分可得裂纹扩展寿命：

式中，a0代表初始裂纹尺寸，af代表最终裂纹尺寸，af可由断裂韧性kic和施加的载荷p进行计算。本发明通过将裂纹扩展寿命中的若干参数进行随机化，进而建立涡轮叶片的裂纹扩展寿命随机模型。例如，若考虑a0、af、kic和p为随机变量，则裂纹扩展寿命式(2)可重新表示为写成：

n＝n(x)(3)

式中x表示一个包含m个随机变量的向量。此时，裂纹扩展寿命将是关于随机向量x的随机函数。针对叶片进行概率损伤容限分析，必须得到寿命n的概率分布。目前，因单次裂纹扩展分析通常涉及复杂的网格重剖分以及百万次的循环迭代过程，高效的裂纹扩展寿命分布求解方法对于其实用化至关重要。因裂纹扩展寿命模型具有极强的非线性且裂纹模型参数可能具有较大的不确定性波动，仍然缺乏有效的计算方法对式(3)进行高效求解。本发明将提出一种仅需少量计算裂纹扩展寿命即可得到其概率分布的高效计算方法。

第二步：间接求解策略。由于裂纹扩展寿命模型具有极强的非线性，通常很难直接准确地获取n(x)的pdf。因log函数能够压缩数据尺度的基础上不改变原有函数的特性，对数化后的裂纹扩展寿命与输入参数间的非线性程度被极大降低。因此，本发明先对n(x)进行对数化，并将对数化后的裂纹扩展寿命作为一个中间量。然后，通过求解中间量的概率分布间接推导得到n(x)的概率分布。对数化后的裂纹扩展寿命可表达如下：

n′(x)＝logn(x)(4)

根据概率理论，n(x)的cdf可由下式求解：

式中f(n)表示n(x)的累计分布函数，fn(n)表示n(x)的概率密度函数，联合式(4)与式(5)可得：

式中fn′(n′)表示n′(x)的pdf。针对上式进行微分可得到n(x)的pdf：

将式(7)代入式(5)有：

最后，n(x)的pdf与cdf都可由n′(x)推导出来。该间接求解策略将具有极强非线性的概率裂纹扩展寿命预测问题转化为非线性一般的概率对数化裂纹扩展寿命预测问题，克服了原非线性特性带来的求解难题。

第三步：随机变量转换。由于裂纹扩展模型中，裂纹扩展常数c和m之间通常存在相关性关系，而裂纹扩展常数与载荷之间又相互独立。针对这种既存在相关变量，又存在独立变量的情形，本发明首先利用nataf变换将随机变量转化为具有相关性的标准正态变量：

[y；ρ′]＝nataf[x；ρ](9)

式中nataf[·]表示nataf变化，ρ和ρ′分别表示x和y的相关系数矩阵。将式(9)代入式(4)中，n′(x)可由下式表示：

n′(x)＝n′(nataf^-1(y))(10)

式中nataf^-1[·]为nataf[·]的逆函数。通过下式求解ρ′的特征值：

[a,d]＝eig(ρ′)(11)

式中eig(·)表示矩阵的特征值分解，a和d分别表示特征值与特征向量矩阵，且a^ta＝i，i表示单位矩阵。然后基于正交变化，相关的标准正态变量y可转换成独立的标准正态变量y′：

因为a^t＝a^-1，将式(12)代入式(10)中，n′(x)可重新表示为：

通过上述转换，非正态的相关变量被转换成独立的标准正态变量。为了方便后续的矩分析，确保任何连续性分布都可由高斯埃尔米特积分求解，独立标准正态分布n(0,1)进一步被转换成服从n(0,1/2)的正态分布：

式中φy(·)表示y的cdf，表示u的累计分布函数的反函数。将式(14)代入式(13)中有：

式中φu(·)表示u的cdf，表示y的累计分布函数的反函数。此时，n′(x)可表示为服从n(0,1/2)的标准正态变量。

第四步：降维矩分析。n′(x)的l阶原点矩可表示为：

式中fx(x)表示x的pdf；e表示期望算子。假设z(u)＝[n′(t^-1(u))]^l，式中基于此，n′(x)的l阶原点矩可表示为：

式中fu(u)表示u的联合概率密度函数。式(17)为一多维积分问题，难以通过解析方法获取。本发明通过引入先进的二维降维积分方法来求解上述多维积分，将裂纹扩展寿命多维积分转换为低维积分。根据二维降维积分方法，z(u)可表示为：

式中k1,k2＝1,2,...,m且k1＜k2，是取决于第k1和k2个随机变量和的随机响应，z(0,...,0,uk,0,...,0)是取决于第k个随机变量uk的随机响应。uk的pdf为进而式(18)可由下式求解：

采用高斯艾尔米特求积公式，一维积分可由下式求解：

式中wq和hq分别表示积分权值和积分点，r表示高斯积分点数，将式(15)代入式(21)有：

类似的式(20)可由下式求解：

式中r1与r2分别表示与方向的高斯积分点个数，wp和wq分别表示积分权值，hp和hq分别表示相应的积分点。将式(22)和式(23)代入式(18)中可求得n′(x)的各阶原点矩。进而可由下式求得n′(x)的各阶中心距κl,l＝1,2,3,4：

第五步：疲劳扩展寿命分布预测。基于矩分析结果，n′(x)的pdf与cdf可进一步由mep求解,n′(x)首先被转换成标准正态变量：

β＝(n′(x)-μn′(x))/σn′(x)(25)

式中μn′(x)与σn′(x)分别表示n′(x)的均值和标准差，根据mep，β的pdf应该满足下式：

式中mβi,i＝1,2,...,4表示β的原点矩，可由其相应的中心距κi,i＝1,2,...,4求解；式中未知系数ai,i＝0,1,...,4可由式(23)求解。进而，n′(x)的pdf可由下式求解：

将上式代入式(7)中，可求解n(x)的pdf:

进而将上式代入式(8)可求得n(x)的cdf:

由此即可求解n(x)的pdf和cdf。

本发明的有益效果在于以下几点：

1.本发明方法针对叶片裂纹扩展寿命模型的强非线性及各参数间的大不确定性与相关性等问题，提出了一种裂纹扩展寿命的概率分析方法，仅需少量确定性裂纹扩展分析即可准确获取裂纹扩展寿命分布。

2.本发明方法针对部分参数存在相关性问题，先利用nataf变换将随机变量转化为具有相关性的正态变量，然后利用正交变化将相关的正态变量转换为独立正态变量，最终转换成服从n(0,1/2)的正态分布，确保任何连续性分布都可由高斯埃尔米特积分求解，提高了求解效率。该方法可同时考虑独立和相关随机变量，且解决了参数的大不确定性问题，推动涡轮叶片损伤容限不确定性分析的工程实用化。

附图说明

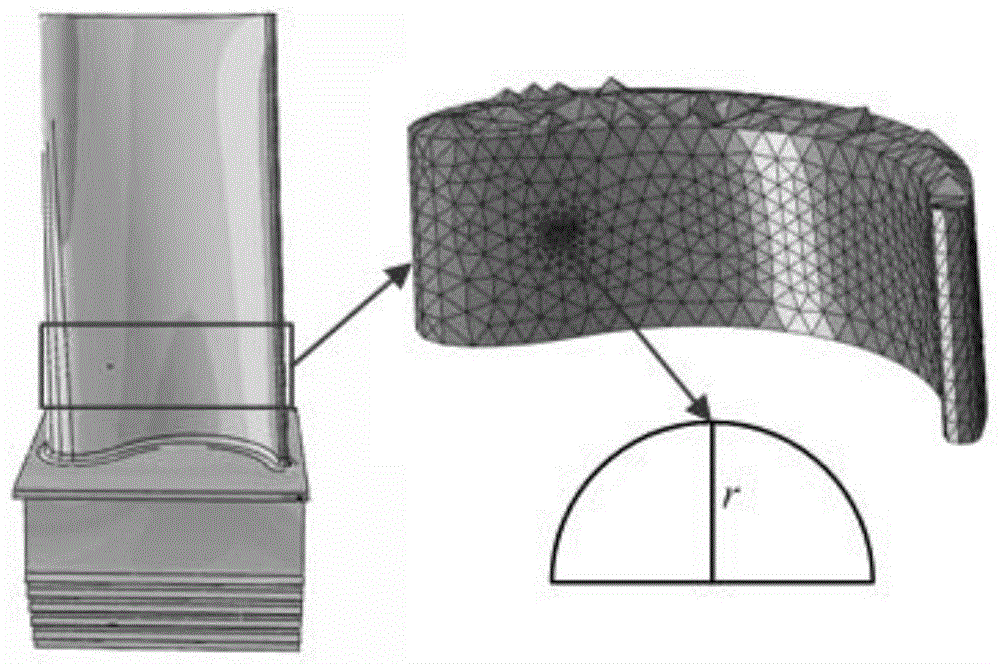
图1叶片整体模型及引入裂纹的子模型。

图2sifs随裂纹长度变化及三维裂纹扩展轮廓线。

图3叶片裂纹扩展寿命pdf。

图4叶片裂纹扩展寿命cdf。

具体实施方式

下面结合实施例及附图，对本发明作进一步地的详细说明，但本发明的实施方式不限于此。

第一步：首先对该涡轮叶片进行确定性三维裂纹扩展分析，叶片整体有限元模型及引入裂纹后的局部子模型如图1所示：模型长75.8mm，宽43.6mm，厚度为15.4mm。有限元模型包含96287个c3d10单元，143824个节点，初始裂纹尺寸为0.5mm，推力为544.1n，弯矩为400nm。叶片材料为aisi450钢，裂纹扩展速率常数c为2.0349e-8，m为3.45，断裂韧性kic为本发明利用abaqus与franc3d相结合对涡轮叶片其进行确定性裂纹扩展分析。首先，通过abaqus分析叶片全局模型获取裂纹尖端位移场，然后通过franc3d读取裂纹尖端位移结果，运用线弹性断裂力学方法计算裂纹尖端海滩条带上的sifs，获取裂纹扩展步长和裂纹扩展方向，确定下一步裂纹尖端前沿位置，更新裂纹扩展模型。经过59个裂纹扩展分析步后，叶片达到断裂韧性而失效。裂纹扩展分析过程及结果如图2所示：图2(a)表示齿轮裂纹尖端sifs与裂纹长度的关系；图2(b)表示齿轮内部裂纹的形状，ki表示相应裂纹前缘轮廓线上sifs的最大值。从图中可以看出，该裂纹扩展模式为i型断裂，随着裂纹长度的增长，裂纹尖端i型sifs逐渐增大，ii型和iii型sifs基本接近于零。由于sifs与载荷成正比关系，由此可得到任意载荷工况下的sifs随裂纹长度变化情况。最终，利用paris公式对图2(a)中的a-k关系积分可获得叶片疲劳裂纹扩展寿命。

第二步：根据专家的经验和已有的有限信息，确定影响涡轮叶片裂纹扩展寿命的概率参数其具体分布和不确定性水平如表1所示。涡轮叶片的疲劳裂纹扩展寿命可表达如下：

n＝n(x)(1)

为了减少不确定性传播过程中的误差传递，先将裂纹扩展寿命功能函数对数化：

n′(x)＝logn(x)(2)

表1涡轮叶片中随机参数分布

第三步：由于裂纹扩展模型中，裂纹扩展常数c和m之间通常存在相关性关系，而裂纹扩展常数与载荷之间又相互独立。针对这种既存在相关变量，又存在独立变量的情形，本发明首先利用nataf变换将随机变量转化为具有相关性的正态变量：

[y；ρ′]＝nataf[x；ρ](3)

式中nataf[·]表示nataf变化，ρ和ρ′分别表示x和y的相关系数矩阵。通过以上转换，n′(x)可由下式表示：

n′(x)＝n′(nataf^-1(y))(4)

式中nataf^-1[·]为nataf[·]的逆函数。然后基于正交变化，相关的正态变量y可转换成独立的正态变量y′，最终转换成服从n(0,1/2)的正态分布：n′(x)可表示为：

后续在空间u将对疲劳裂纹扩展寿命进行分析。

第四步：n′(x)的l阶原点矩可表示为：

式中fx(x)表示x的pdf；e表示期望算子。假设z(u)＝[n′(t^-1(u))]^l，式中通过二维降维积分方法，n′(x)的l阶原点矩可由下式求解：

式中r1与r2分别表示与方向的高斯积分点个数，wp和wq分别表示积分权值，hp和hq分别表示相应的积分点。

第五步：n′(x)的pdf可进一步由mep求解：

再将对数化的函数转回到原空间得到n(x)的pdf:

进而可求得n(x)的cdf:

本发明预测的疲劳扩展寿命的pdf与cdf分别如图3与图4所示。为了验证本发明方法的精度，采用1e6个样本对涡轮叶片疲劳寿命模型进行蒙特卡洛仿真(mcs)，并将其预测结果作为参考解。从图3与图4可发现，本发明方法与mcs预测的结果具有一致性，但本文方法仅需127次确定性的疲劳寿命分析。结果表明了本文方法可在保障概率疲劳裂纹扩展寿命预测精度的同时极大地提高计算效率。基于求得的cdf，我们可以估计叶片在受到疲劳加载时任意周次下的安全可靠度，进而对叶片的经济性检修周期进行评估，保障结构的安全可靠性。另外，该方法可以与等效初始裂纹尺寸分布相结合来分析叶片疲劳安全可靠性及其耐久性，从而确保涡轮叶片的服役安全。