一种边数可设定的对轮廓曲线的多边形简化方法与流程

本发明涉及数字图像处理技术领域，尤其涉及一种边数可设定的对轮廓曲线的多边形简化方法。

背景技术：

目前，数字摄像机或其它数字设备采集到的图像大多为光栅图，当需要对图像上的物体进行识别、测量等操作时，首先需要对物体的边界进行识别和存储，通过数字图像处理技术，将物体边界识别为轮廓曲线。物体的形状各不相同，加之镜头畸变、观察角度、识别误差等因素，得到的轮廓线也各不相同，通常是由非规则的线段、曲线构成，即使是规则外形的物体其轮廓也是如此，可统一视作轮廓曲线。要对这些轮廓曲线进行记录，需要沿轮廓曲线逐个像素点进行记录，不但耗费巨大的存储空间，也难以进一步对其进行模式识别、形状匹配、形态描述、长度、周长及面积测量计算等操作。因此，在实际过程中经常需要对轮廓曲线进行多边形简化，即去除轮廓曲线上大量的点，只需找到少量的“关键点”，并依次两两直连而得到一个封闭多边形(对于封闭的轮廓曲线)或一条折线(对于非封闭轮廓曲线)即可，这里统称为多边形简化。简化得到的多边形与原轮廓曲线在形状、尺寸上虽有一定误差，但基本相近，具体误差取决于具体的简化方法、参数设定及评价方法。

目前广泛使用的对轮廓曲线的多边形简化方法是1973年提出的douglas-peucker方法，目前广泛使用的计算机视觉函数库opencv所支持的approxpolydp()函数采用的就是douglas-peucker方法。然而，douglas-peucker方法只能设定轮廓曲线与简化后的多边形的最远距离误差，即轮廓曲线上的点到简化后多边形上对应边的最远距离，设为epislon，但无法预知在设定距离误差epislon下所生成的简化多边形的边数x；此外由于轮廓曲线的形状、尺寸方面千差万别，在应用douglas-peucker方法时，想要得到指定边数的多边形，对最远距离误差epislon的预先设定也是一个难题，需要使用者凭借大量经验或反复试验才能确定。相比较而言，使用本发明所提出的approxployyh方法，使用者可直接设定对轮廓曲线简化后所得到多边形的最终边数，用指定边数的多边形对轮廓曲线进行简化表示。

技术实现要素：

本发明针对上述现有技术的不足，提供一种边数可设定的对轮廓曲线的多边形简化方法，简称approxployyh方法，用于数字图像里的轮廓曲线进行模式识别与匹配、几何校正、数据压缩、矢量化表示等，进一步可应用于对数字图像中轮廓曲线的周长、面积等方面的测量与计算。

本发明所采取的技术方案是：一种边数可设定的对轮廓曲线的多边形简化方法，包括以下步骤：

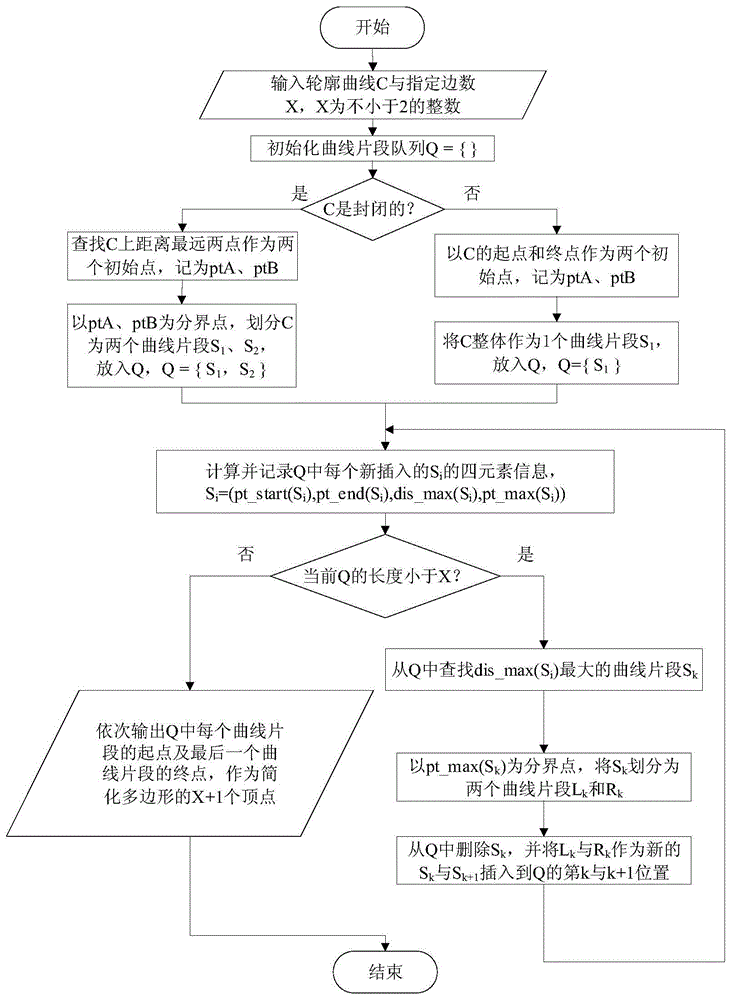
步骤1：多边形简化参数初始化设定：对于给定的待简化轮廓曲线，记为c，设定简化后多边形的边数x，其中x为不小于2的整数；若c为封闭轮廓曲线，则x表示简化后的封闭多边形的边数，即顶点数；若c为非封闭轮廓曲线，简化后的多边形实际是非封闭的折线，x则代表折线的边数，比顶点数少1，此时非封闭的折线顶点包括该折线的折点和端点；初始化曲线片段队列q为空，即q＝{}；

前述边数可设定的对轮廓曲线的多边形简化方法简称approxployyh方法；前述轮廓曲线用c来表示，将其视作由一个或多个曲线片段首尾衔接连接而成，即用队列q＝{s1，s2，s3，…，sn}的形式来表示，即由顺序排列的n个曲线片段s1、s2、…、sn连接而成；轮廓曲线是连续的，即相邻的曲线片段是首尾衔接的，即si的终点坐标pt_end(si)与si+1的起点坐标pt_start(si+1)重合；轮廓曲线可以是封闭的，即sn的终点坐标pt_end(sn)与s1的起点坐标pt_start(s1)重合；轮廓曲线也可以是不封闭的，即pt_end(sn)与pt_start(s1)不重合，这时该轮廓曲线实质上是一条平面或三维空间内的非封闭曲线；轮廓曲线不可以是自交叉的，其所有的曲线片段两两之间都不存在交叉点；

步骤2：对待简化轮廓曲线进行初始点查找：若c为封闭轮廓曲线，则查找c上距离最远的两个点，作为初始两个点；若c为非封闭轮廓曲线，则以c的两个端点作为初始两个点；初始两个点记为pta、ptb；

步骤3：对待简化轮廓曲线进行轮廓曲线初始分割：以pta、ptb为分界点，对c进行分割；若c为封闭轮廓曲线，则c被分割成2个曲线片段，记为s1、s2，此时s1和s2首尾相接且形成封闭曲线，即s2起点pt_start(s2)与s1终点pt_end(s1)重合并且s2终点pt_end(s2)与s1起点pt_start(s1)重合，将s1和s2依次放入曲线片段队列q，即q＝{s1，s2}；若c为非封闭轮廓曲线，则c整体作为1个曲线片段，记为s1，放入曲线片段队列q，即q＝{s1}；

前述曲线片段为由多个连续点组成的一个任意形状的连续的线条；当曲线片段所有点都在同一平面内时该线条为二维，当曲线片段所有点都在同一三维空间内时该线条为三维，但不共平面；该线条只有一个起点、一个终点，起点和终点不重合，也不存在分叉情况；该线条既不封闭，也不自交叉，即任意两个点的位置都不重合；该线条上的所有点的位置测量后用二维或三维坐标描述；设曲线片段用s＝(pt_start(s)，pt_end(s)，dis_max(s)，pt_max(s))的四元素的形式来表示，其中s代表曲线片段，pt_start(s)表示s的起点坐标，pt_end(s)表示s的终点坐标，dis_max(s)和pt_max(s)分别表示s上的最大点弦距及其在s上对应点的坐标，即对于线条s上所有的点而言，若某点距离s的弦线最远，即该点到过点pt_start(s)和pt_end(s)的直线的距离最远，则取该点记为pt_max(s)，对应的点弦距记为dis_max(s)；

步骤4：对曲线片段四元素信息进行计算：对于新插入队列q中的每一个曲线片段si，计算其对应的dis_max(si)及pt_max(si)，形成并记录其完整的四元素信息，即si＝(pt_start(si)，pt_end(si)，dis_max(si)，pt_max(si))，其中si代表曲线片段，pt_start(si)表示si的起点坐标，pt_end(si)表示si的终点坐标，dis_max(si)和pt_max(si)分别表示si上的最大点弦距及其在si上对应点的坐标；

步骤5：对结束条件进行判断及输出简化后结果：记当前曲线片段队列q的长度为n，即q＝{s1，s2，s3，…，sn}；若n等于x，则依次输出曲线片段s1、s2、s3、…、sn的起点以及sn的终点，作为简化多边形p＝{pt1，pt2，pt3，…，ptx，ptm}的x+1个顶点，其中pt1＝pt_start(s1)，pt2＝pt_start(s2)，pt3＝pt_start(s3)，…，ptx＝pt_start(sn)，ptm＝pt_end(sn)；若c为封闭轮廓曲线，则此时sn终点与s1起点相同，即ptm与pt1重合，若c为非封闭轮廓曲线，则此二点不重合；至此，完成了对轮廓曲线c的简化描述过程，即用p中的x+1个顶点连成的x条边的多边形完成了对给定轮廓曲线c的简化描述，过程结束；若n小于x则跳转至步骤6；

其中对于给定的轮廓曲线c，将其简化为多边形p＝{pt1，pt2，pt3，…，ptx，ptm}的形式，实际上m＝x+1；其中，p代表简化后的多边形，是平面的或三维的，由m个顺序排列的点pt1、pt2、…、ptx、ptm顺序连接而成；若c为封闭的，则p为封闭的，即pt1与ptm位置重合；若c为非封闭的，则p为非封闭的，即pt1与ptm位置不重合；前述多边形简化，是指p的边数小于轮廓曲线c上的点数，即用少量边的多边形来表示c；本发明边数可设定的对轮廓曲线的多边形简化，是指简化得到的多边形p的边数可任意指定，设为x，x为不小于2的整数，由使用者根据其需求指定；

步骤6：对最大点弦距曲线片段进行查找与分割：从队列q中查找dis_max(si)最大的一个曲线片段，记为sk，即当前q中所有的曲线片段中第k个曲线片段的最大点弦距最大，即dis_max(sk)最大；以pt_max(sk)为分界点，把曲线片段sk一分为二，变成两个新的曲线片段lk和rk，其中lk的起点和终点坐标分别为pt_start(sk)和pt_max(sk)，rk的起点和终点坐标分别为pt_max(sk)、pt_end(sk)，之后把sk从队里q中删除，再把lk和rk插入q中第k和第k+1的位置，作为新的sk和sk+1，此时q的长度增加1；

步骤7：迭代返回，返回至步骤4继续执行。

采用上述技术方案所产生的有益效果在于：本发明提供的一种边数可设定的对轮廓曲线的多边形简化方法，解决了传统的douglas-peucker方法(对应于目前广泛使用的计算机视觉函数库opencv中的approxpolydp()函数)无法直接按照指定边数对轮廓曲线进行多边形简化的缺陷，本发明与douglas-peucker方法相比，使用者只需要设定简化后多边形的边数即可，无需预先知道或反复调整距离误差epislon；本发明适用于任意给定的不自交叉的轮廓曲线，可以是封闭或不封闭的，可按使用者指定边数直接生成简化后的多边形表示，大大压缩了轮廓曲线数据，显著提升了图像处理过程中对轮廓曲线的简化表示的处理效率。

本发明可控性高，可任意指定简化后多边形的边数，使用简单，无需预先设定简化后的最大距离误差；适用性好，适用于任何不自交叉的轮廓曲线的多边形简化表示，包括封闭和不封闭的；计算简单，便于用计算机实现，对软硬件要求不高，代价小、效率高。

附图说明

图1为本发明多边形简化方法流程图；

图2为本发明实施例中对封闭轮廓曲线指定6条边的简化过程图；

图3为本发明实施例中对封闭轮廓曲线指定6条边的简化结果图；

图4为本发明实施例中对非封闭轮廓曲线指定5条边的简化过程图；

图5为本发明实施例中对非封闭轮廓曲线指定5条边的简化结果图；

图6为douglas-peucker方法对封闭轮廓曲线指定epislon范围为25～43的简化结果图；

图7为douglas-peucker方法对非封闭轮廓曲线指定epislon范围为48～95的简化结果图；

具体实施方式

下面结合附图和实施例，对本发明的具体实施方式作进一步详细描述。以下实施例用于说明本发明，但不用来限制本发明的范围。

一种边数可设定的对轮廓曲线的多边形简化方法，如图1所示，包括以下步骤：

步骤1：多边形简化参数初始化设定：对于给定的待简化轮廓曲线，记为c，设定简化后多边形的边数x，其中x为不小于2的整数；若c为封闭轮廓曲线，则x表示简化后的封闭多边形的边数，即顶点数；若c为非封闭轮廓曲线，简化后的多边形实际是非封闭的折线，x则代表折线的边数，比顶点数少1，此时非封闭的折线顶点包括该折线的折点和端点；初始化曲线片段队列q为空，即q＝{}；

前述轮廓曲线用c来表示，将其视作由一个或多个曲线片段首尾衔接连接而成，即用队列q＝{s1，s2，s3，…，sn}的形式来表示，即由顺序排列的n个曲线片段s1、s2、…、sn连接而成；轮廓曲线是连续的，即相邻的曲线片段是首尾衔接的，即si的终点坐标pt_end(si)与si+1的起点坐标pt_start(si+1)重合；轮廓曲线可以是封闭的，即sn的终点坐标pt_end(sn)与s1的起点坐标pt_start(s1)重合；轮廓曲线也可以是不封闭的，即pt_end(sn)与pt_start(s1)不重合，这时该轮廓曲线实质上是一条平面或三维空间内的非封闭曲线；轮廓曲线不可以是自交叉的，其所有的曲线片段两两之间都不存在交叉点；

步骤2：对待简化轮廓曲线进行初始点查找：若c为封闭轮廓曲线，则查找c上距离最远的两个点，作为初始两个点；若c为非封闭轮廓曲线，则以c的两个端点作为初始两个点；初始两个点记为pta、ptb；

步骤3：对待简化轮廓曲线进行轮廓曲线初始分割：以pta、ptb为分界点，对c进行分割；若c为封闭轮廓曲线，则c被分割成2个曲线片段，记为s1、s2，此时s1和s2首尾相接且形成封闭曲线，即s2起点pt_start(s2)与s1终点pt_end(s1)重合并且s2终点pt_end(s2)与s1起点pt_start(s1)重合，将s1和s2依次放入曲线片段队列q，即q＝{s1，s2}；若c为非封闭轮廓曲线，则c整体作为1个曲线片段，记为s1，放入曲线片段队列q，即q＝{s1}；

前述曲线片段为由多个连续点组成的一个任意形状的连续的线条；当曲线片段所有点都在同一平面内时该线条为二维，当曲线片段所有点都在同一三维空间内时该线条为三维，但不共平面；该线条只有一个起点、一个终点，起点和终点不重合，也不存在分叉情况；该线条既不封闭，也不自交叉，即任意两个点的位置都不重合；该线条上的所有点的位置测量后用二维或三维坐标描述；设曲线片段用s＝(pt_start(s)，pt_end(s)，dis_max(s)，pt_max(s))的四元素的形式来表示，其中s代表曲线片段，pt_start(s)表示s的起点坐标，pt_end(s)表示s的终点坐标，dis_max(s)和pt_max(s)分别表示s上的最大点弦距及其在s上对应点的坐标，即对于线条s上所有的点而言，若某点距离s的弦线最远，即该点到过点pt_start(s)和pt_end(s)的直线的距离最远，则取该点记为pt_max(s)，对应的点弦距记为dis_max(s)；

步骤4：对曲线片段四元素信息进行计算：对于新插入队列q中的每一个曲线片段si，计算其对应的dis_max(si)及pt_max(si)，形成并记录其完整的四元素信息，即si＝(pt_start(si)，pt_end(si)，dis_max(si)，pt_max(si))，其中si代表曲线片段，pt_start(si)表示si的起点坐标，pt_end(si)表示si的终点坐标，dis_max(si)和pt_max(si)分别表示si上的最大点弦距及其在si上对应点的坐标；

步骤5：对结束条件进行判断及输出简化后结果：记当前曲线片段队列q的长度为n，即q＝{s1，s2，s3，…，sn}；若n等于x，则依次输出曲线片段s1、s2、s3、…、sn的起点以及sn的终点，作为简化多边形p＝{pt1，pt2，pt3，…，ptx，ptm}的x+1个顶点，其中pt1＝pt_start(s1)，pt2＝pt_start(s2)，pt3＝pt_start(s3)，…，ptx＝pt_start(sn)，ptm＝pt_end(sn)；若c为封闭轮廓曲线，则此时sn终点与s1起点相同，即ptm与pt1重合，若c为非封闭轮廓曲线，则此二点不重合；至此，完成了对轮廓曲线c的简化描述过程，即用p中的x+1个顶点连成的x条边的多边形完成了对给定轮廓曲线c的简化描述，过程结束；若n小于x则跳转至步骤6；

其中对于给定的轮廓曲线c，将其简化为多边形p＝{pt1，pt2，pt3，…，ptx，ptm}的形式，实际上m＝x+1；其中，p代表简化后的多边形，是平面的或三维的，由m个顺序排列的点pt1、pt2、…、ptx、ptm顺序连接而成；若c为封闭的，则p为封闭的，即pt1与ptm位置重合；若c为非封闭的，则p为非封闭的，即pt1与ptm位置不重合；前述多边形简化，是指p的边数小于轮廓曲线c上的点数，即用少量边的多边形来表示c；本发明边数可设定的对轮廓曲线的多边形简化，是指简化得到的多边形p的边数可任意指定，设为x，x为不小于2的整数，由使用者根据其需求指定；

步骤6：对最大点弦距曲线片段进行查找与分割：从队列q中查找dis_max(si)最大的一个曲线片段，记为sk，即当前q中所有的曲线片段中第k个曲线片段的最大点弦距最大，即dis_max(sk)最大；以pt_max(sk)为分界点，把曲线片段sk一分为二，变成两个新的曲线片段lk和rk，其中lk的起点和终点坐标分别为pt_start(sk)和pt_max(sk)，rk的起点和终点坐标分别为pt_max(sk)、pt_end(sk)，之后把sk从队里q中删除，再把lk和rk插入q中第k和第k+1的位置，作为新的sk和sk+1，此时q的长度增加1；

步骤7：迭代返回，返回至步骤4继续执行。

实施例1：对封闭轮廓曲线进行多边形简化，如图2、图3所示给出了应用本发明approxpolyyh方法对一个封闭轮廓曲线指定6条边的多边形简化过程及结果的实施例；给定待简化的轮廓曲线，记为c，初始化轮廓曲线队列q＝{}；查找c上距离最远两点，记为pta和ptb；以pta、ptb为分界点把c进行分割分成两段新的曲线片段，记为s1、s2，其中四元素表示s1＝(pta,ptb,d2,ptd)，s2＝(ptb,pta,d1,ptc)，把s1和s2依次放入队列q，即q＝{s1，s2}；从q中查找具有最大点弦距的曲线片段s2，以其最大点弦距所对应的点ptc为分割点将s2分割为l2和r2，即l2＝(ptb,ptc,d4,pte)，r2＝(ptc,pta,d3,ptg)，将s2从q中删除，把l2和r2插入q中原来s2所在的位置，成为新的s2和s3，即此时q＝{s1，s2，s3}；重复上述最大点弦距的查找及对应曲线片段的分割步骤，直至q的长度达到6，即q中曲线片段为6个，此时依次输出q中各曲线片段的起点以及最后一个曲线片段的终点，即pta、ptd、ptf、ptb、pte、ptc、pta作为封闭的简化多边形p的顶点，至此，完成了对轮廓曲线c的多边形简化。

实施例2：非封闭轮廓曲线的多边形简化，如图4、图5所示给出了应用本发明approxpolyyh方法对一个非封闭轮廓曲线指定5条边的多边形简化过程及结果的实施例。

将本发明与douglas-peucker方法比较，如图6所示给出了douglas-peucker方法当epislon取值25～43范围内的对同一封闭轮廓曲线简化结果图，如图7所示给出了douglas-peucker方法当epislon取值48～95范围内对同一非封闭轮廓曲线的简化结果图。分析比较图2～图7可以看出，approxpolyyh方法可达到与douglas-peucker方法基本一致的简化精度和结果，但使用上要方便很多：要对轮廓曲线进行指定边数的多边形简化表示，采用approxpolyyh方法直接输入指定边数即可，无需预先知道epislon，而douglas-peucker方法不能直接完成指定边数多边形的简化，需预先确定简化后精度epislon的大小，这需要使用者凭借大量经验或反复试验调整才能确定。

最后应说明的是：以上各实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述各实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分或者全部技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明权利要求所限定的范围。