基于多尺度的时滞神经网络滞后分岔分析方法与流程

本发明涉及一种基于多尺度的时滞神经网络滞后分岔现象分析方法，属于时滞神经网络分岔现象分析领域。

背景技术：

目前，在神经网络系统动力学性质的研究中，利用一些典型的人工神经网络模型来揭示时滞导致的各种复杂动力学行为产生的机理，以便更好地认清神经活动的规律是一项非常重要的工作。时滞常导致系统的运动失稳，产生各种形式的分岔。在非线性时滞动力学系统的分岔中，hopf分岔是普遍存在的，且是讨论得最为广泛的。研究hopf分岔周期解的性质通常采用中心流形约化方法与规范型理论，该方法在理论上比较完备，但过程繁琐且计算量大。故提出一种简单、成本少的时滞神经网络中滞后分岔分析方法是很有必要的。任何发生hopf分岔的系统都可以用stuart-landau方程来研究，且解stuart-landau方程比分析整个系统要简单的多。因此，提出一种基于多尺度思想得到stuart-landau方程，从而对时滞神经网络中滞后分岔现象进行分析的方法。

技术实现要素：

本发明的目的是：分析时滞神经网络中的滞后分岔现象，特别是亚临界hopf分岔引起的滞后分岔，采用多尺度的思想，在分岔点附近进行扰动分析，将时间尺度放慢，得到放慢尺度后的一到五阶方程，然后逐级求解非线性方程，通过奇数阶方程的求解得到stuart-landau方程，用伴随法得到landau系数。根据stuart-landau方程来描述分岔点附近的弱非线性动力学。

为了达到上述目的，本发明的技术方案是提供了一种基于多尺度的时滞神经网络滞后分岔分析方法，其特征在于，包括以下步骤：

步骤1、变换原始模型，建立新的零平衡点的状态空间方程；

步骤2、采用多尺度方法在hopf分岔点处进行非线性扩展，进行非线性扩展时，重新定义分岔参数μ，μ＝μc+ε²δ2，式中，μc是hopf分岔点；ε是一个量化靠近hopf点的振荡幅度的一个小数量，0＜ε＜1；参数δ2根据hopf点的一侧取±1的值，将步骤1获得的状态空间方程展开为ε的幂级数形式，将时间尺度放慢，然后将其作用于展开为ε的幂级数形式的状态空间方程，求出各项的ε的同次幂系数，重新排列后根据ε的同次幂系数得到ε的一到五阶方程；

步骤3、分别求解步骤2中得到的ε的各阶方程，得到三阶stuart-landau方程和五阶stuart-landau方程；

步骤4、根据步骤3中得到的三阶stuart-landau方程和五阶stuart-landau方程，描述分岔点附近的弱非线性动力学。

优选地，步骤2中，所述时间尺度由t0(t0＝t)和慢尺度t2、t4构成。

优选地，步骤2中，所述一到五阶方程为五个线性非齐次微分方程。

与传统的一些方法相比，本发明能够简化对非线性方程的求解，只需要推导出三阶stuart-landau方程，就能够描述分岔点附近的震荡幅度的变化，而通过五阶stuart-landau方程，能够获得双稳态区域的位置以及不稳定和稳定极限环的振幅的解析表达式，同时，解stuart-landau方程比解整个非线性系统要快的多。该方法可以减少在数值模拟和实验中研究hopf分岔附近的震荡和次临界现象的成本，并且与完全非线性分析之间有良好的一致性。

附图说明

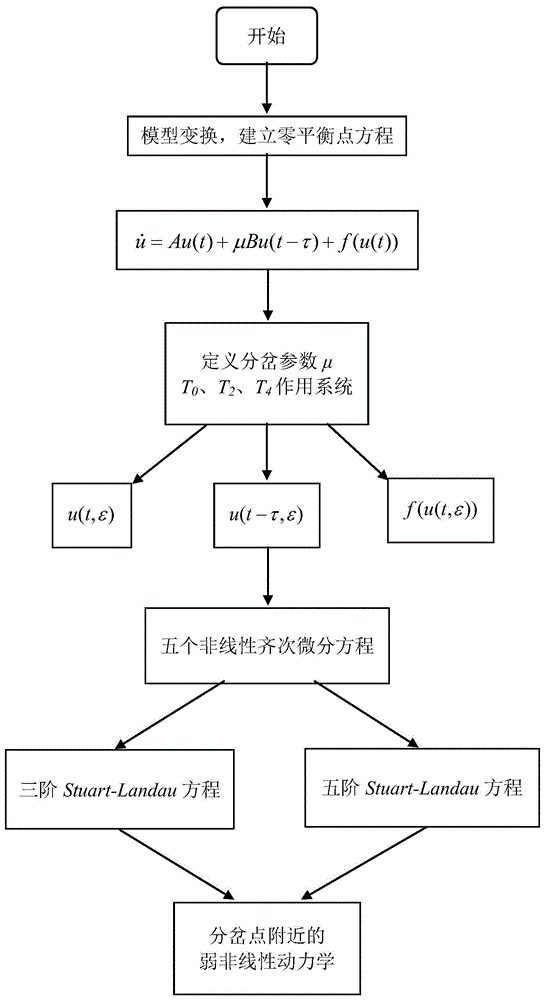
图1为本发明的流程图。

具体实施方式

下面结合具体实施例，进一步阐述本发明。应理解，这些实施例仅用于说明本发明而不用于限制本发明的范围。此外应理解，在阅读了本发明讲授的内容之后，本领域技术人员可以对本发明作各种改动或修改，这些等价形式同样落于本申请所附权利要求书所限定的范围。

本发明提供的一种基于多尺度的时滞神经网络滞后分岔分析方法包括以下步骤：

步骤1、变换原始模型，建立新的零平衡点的状态空间方程；

步骤2、采用多尺度方法在hopf分岔点处进行非线性扩展，重新定义分岔参数，将时间尺度放慢，由t0(t0＝t)和慢尺度t2、t4构成，然后将其作用于系统。重新排列后根据ε的同次幂系数得到ε的一到五阶方程。

步骤3、分别求解步骤2中得到的ε的各阶方程，得到三阶和五阶的stuart-landau方程。

步骤4、根据步骤3中得到的三阶和五阶stuart-landau方程，描述分岔点附近的弱非线性动力学。

以基于fitzhugh方程的两个神经元的时滞神经网络的分岔分析为例：

步骤1、新新的零平衡点的状态空间方程的建立，具体步骤是：

步骤1.1、考虑基于fitzhugh方程的两个神经元的时滞神经网络，如下式所示：

其中，ρ、a、b为正实数，0＜ρ＜1；，，0＜b＜1，1-2b/3＜a＜1；v和w代表膜电位和失活变量；i代表膜电流，当产生动作电位时，突触将在突触后膜上引入电流，当突触为兴奋的时候，i为正，当突触为抑制的时候，i为负，对于所有i，该模型都有一个唯一的平衡点(v0,w0)。

步骤1.2、修改模型模拟突触反馈：

由于突触的传导速度限制，膜电流的出现会有延迟，此外，由于电流是离子性的，我们希望其大小大致和v与“静止电位”v0的距离成比例，则可以修改步骤1.1的模型来模拟突触反馈，如下式所示：

其中，τ表示时间延迟参数，τ＞0；μ对兴奋性反馈为正，对抑制性反馈为负，反馈强度由μ的大小度量；对于μ＝0和所有的τ，在(v0,w0)处具有稳定的平衡点。

步骤1.3、根据步骤1.2的微分-差分方程组，得到新的状态空间模型：

令x＝v-v0，y＝w-w0和u＝(x,y)^t，将步骤1.2的模型变换到零平衡点，如下式所示：

其中

步骤2、采用多尺度思想对分岔点附近进行非线性扩展，具体步骤是：

步骤2.1、重新定义分岔参数μ，将步骤1.3的解u展开为幂级数的形式：

定义μ＝μc+ε²δ2，其中，μc是hopf分岔点；0<ε<1是一个量化靠近hopf点的振荡幅度的一个小数量；参数δ2可以根据我们正在研究的hopf点的一侧取±1的值。寻求表示为ε的幂级数的解u：

u＝εu1+ε²u2+ε³u3+ε⁴u4+ε⁵u5+ο(ε⁶)

式中，u1、u2、u3、u4、u5表示u展开后ε各阶的系数，ο(ε⁶)表示大于5阶的高次项，因为只需要扩展到五阶，计算时可将5阶之后的项舍去。

步骤2.2、使用快速时间标度t0、慢时间尺度t2和t4作用于系统：

在μ＝μc的邻域中：

其中，t0＝t,t2＝ε²t,t4＝ε⁴t。关于t的导数转换为：

方程其他项变为：

将u(t-τ,ε)以ε扩展为：

u(t-τ,ε)＝ε(u1τ+d2u1τ(-ε²τ)+d4u1τ(-ε⁴τ))

+ε²(u2τ+d2u2τ(-ε²τ))+ε³(u3τ+d2u3τ(-ε²τ))

+ε⁴u4τ+ε⁵u5τ

＝εu1τ+ε²u2τ+ε³(u3τ+τd2u1τ)+ε⁴(u4τ+τd2u2τ)

+ε⁵(u5τ+τd2u3τ+τd4u1τ)

其中，uiτ＝ui(t0-τ,t2,t4),i＝1,2,3

步骤2.3、根据步骤2.2求出各项的ε的同次幂系数，得到五个线性非齐次微分方程：

d0u1-au1-μcbu1(t0-τ)＝0

d0u2-au2-μcbu2(t0-τ)＝f2

d0u3-au3-μcbu3(t0-τ)＝-d2u1-τμcbd2u1(t0-τ)+δ2bu1(t0-τ)+f3

d0u4-au4-μcbu4(t0-τ)＝-d2u2-τμcbd2u2(t0-τ)+δ2bu2(t0-τ)+f4

d0u5-au5-μcbu5(t0-τ)＝-d2u3-d4u1-τμcbd2u3(t0-τ)-τμcbd4u1(t0-τ)

+δ2bu1(t0-τ)-τδ2bd2(t0-τ)+f5

步骤3、求解步骤2中得到的线性非齐次微分方程，得到奇数阶stuart-landau方程，包括以下步骤：

步骤3.1、对一阶系数方程求解

d0u1-au1-μcbu1(t0-τ)＝0

这是一个解特征值问题，则上式的通解为

其中ωc是边缘稳定本征模的角频率，是对应的右本征向量，w(t2,t4)是一个复数变量，仅取决于慢时标。上标用于根据对复振幅w得依赖性进行分类。

步骤3.2、对二阶系数方程求解

d0u2-au2-μcbu2(t0-τ)＝f2

将步骤3.1的解u1代入得

其中

c.c.表示括号中之前项的复共轭

通过拟设解得相同形式的解

则获得线性方程组

矩阵和m0是非奇异的，在u2的不同振幅水平上产生解。

步骤3.3、对三阶系数方程求解

d0u3-au3-μcbu3(t0-τ)＝-d2u1-τμcbd2u1(t0-τ)+δ2bu1(t0-τ)+f3

将步骤3.1和步骤3.2中得到的u1、u2代入上式得

为了保证方程有解，则等式右边得长期项必须与伴随矩阵特征向量正交，寻求上式得特殊解则可解条件为：

其中，是伴随矩阵的特征向量。重排上式，可以得到三阶的stuart-landau方程

d2w＝α0w+β0|w|²w

其中，α0、β0为landau系数，定义为

最后通过拟设解得相同形式的解

得到线性方程组

步骤3.4、对四阶系数方程求解

d0u4-au4-μcbu4(t0-τ)＝-d2u2-τμcbd2u2(t0-τ)+δ2bu2(t0-τ)+f4将步骤3.1、步骤3.2和步骤3.3中得到的解代入上式得

通过拟设解得相同形式的解

得到线性方程组

步骤3.5、对五阶系数方程求解

d0u5-au5-μcbu5(t0-τ)＝-d2u3-d4u1-τμcbd2u3(t0-τ)-τμcbd4u1(t0-τ)

+δ2bu1(t0-τ)-τδ2bd2(t0-τ)+f5

将之前步骤的解代入整理得

由步骤3.3，得到可解条件

整理得到五阶的stuart-landau方程：

d4w＝α1w+β1|w|²w+γ1|w|⁴w

其中，α1、β1及γ1为landau系数，定义为，

因为t4＝ε²t2，结合3.3，可以得到

步骤4，根据步骤3所得stuart-landau方程对分岔现象进行分析，包括以下步骤：

步骤4.1、分析三阶stuart-landau方程

将w＝re^iθ代入步骤3.3的d2w并取所得方程的实部和虚部，得到

得到振幅方程的稳定解

对应的特征值是

j(r1)＝re(α0),j(r2)＝-2re(α0)

因此，我们可以根据re(α0)和re(β0)的符号得到以下四种情况：

(a)当re(α0)＜0，re(β0)＞0时，系统具有稳定的不动点和不稳定的极限环。

(b)当re(α0)＞0，re(β0)＞0时，系统有唯一解，是不稳定不动点。

(c)当re(α0)＜0，re(β0)＜0时，系统具有唯一解，是一个稳定的不动点。

(d)当re(α0)＞0，re(β0)＜0时，系统具有不稳定的不动点和稳定的极限环。

根据步骤3，可以得出，当re(β0)＞0，re(α0)变号时，有一个亚临界hopf分岔。同样，当re(β0)＜0时，有一个超临界hopf分叉。

步骤4.2、分析五阶stuart-landau方程

利用极坐标表示w＝re^iθ，代入3.5的并取所得方程的实部和虚部得到五阶范式

其中，α＝α0+ε²α1，β＝β0+ε²β1，γ＝ε²γ1

考虑五阶范式，得到了振幅方程的稳定解

及其对应的特征值

j(r1)＝re(α)

随着分岔参数的增加，发生hopf分岔，随着分岔参数的减小，分岔发生在折叠点，即滞后分岔。只有五阶弱非线性展开才能证明这一点。由此我们还可以得到双稳态区域的范围。

系统在αr＝αh＝0时发生亚临界分岔，在时发生鞍结(折叠)分岔。则滞后区的宽度为

其中αr由和r²＝βr/(2γr)求出。

本发明提出了一种分析时滞神经网络中的滞后分岔现象的方法。该方法计算简单、可以减少在数值模拟和实验中研究hopf分岔附近的震荡和次临界现象的成本，并且与完全非线性分析之间有良好的一致性。