一种起重机n阶伸缩臂架临界载荷的确定方法

1.本发明涉及机械结构设计技术领域，具体涉及一种起重机n阶伸缩臂架临界载荷的确定方法。


背景技术：

2.伴随着现代科学技术的发展，工程结构体系日益趋向大型化、高耸化、轻柔化。阶梯型柱在混凝土泵车臂架体系、起重机吊臂结构、大型钻杆等结构体系中被广泛应用。在大型起重结构体系中，需要的阶梯型吊臂阶数越来越大。由于高强度钢材的使用，提高了构件强度和刚度使得起升高度变大、起重量变大，而稳定问题日显突出，失稳载荷的计算求解成了一个重要的问题。
3.阶梯型柱的屈曲研究是国内外学者研究的热点，对工程实际具有巨大的意义。阶梯型柱的屈曲载荷研究多运用经典方法，如微分方程法、能量法、有限元法、差分法等。timoshenko等利用能量法计算出了二阶阶梯型柱的临界力载荷，也给出了其他一些近似的方法。在计算阶梯柱的段数不大的时候，这些方法的精确度较高。陆念力等应用弹性稳定理论对阶梯变截面构件的两种常见支承，推导出了平衡状态下多节连续构件挠曲微分方程，得到构件失稳特征方程的精确表达式。lellep j等研究了轴向压力作用下阶梯组合柱的稳定性。考虑柱转角处裂纹对矩形截面阶梯柱的稳定性影响，计算了裂纹位置和长度对失稳载荷的影响。q.s.li.提出了一种多阶非均匀柱在集中轴压作用下的弹性屈曲分析方法。建立了屈曲问题的控制微分方程，给出了五种不同类型非均匀柱控制方程的特殊解。刘士明等研究了如何准确计入油缸支撑作用及搭接摩擦力对起重机箱形伸缩臂稳定性影响的分析。利用挠度微分平衡方程，给出起重机箱形伸缩臂三种计算模型的欧拉临界力的分析推导。张月强等利用能量法和最小势能原理对阶梯型柱的临界载荷进行了分析研究，得到阶梯型受压柱的平面内稳定的参数，为实际工程应用提供参考。
4.以上研究主要是用经典方法对经典边界条件下阶梯型柱的屈曲研究，针对较高阶的阶梯柱屈曲的研究较少，而且对于计算高阶阶梯柱屈曲的效率、收敛性和精度有待提高。


技术实现要素：

5.本发明所要解决的技术问题在于针对上述现有技术的不足，提供一种起重机n阶伸缩臂架临界载荷的确定方法，该方法利用新型级数法对起重机伸缩臂架所属的悬臂型阶梯型柱的屈曲载荷进行研究，解决了传统傅里叶级数在边界处存在导数不连续和收敛性差的问题。还能获得任意边界条件下的阶梯型柱屈曲载荷，在精度、计算效率和收敛性方面有了一定的提高，同时也适用一般弹性边界条件。
6.为解决上述技术问题，本发明采用的技术方案是：一种起重机n阶伸缩臂架临界载荷的确定方法，其特征在于，包括以下步骤：
7.s1、建立阶梯柱的屈曲受力模型：
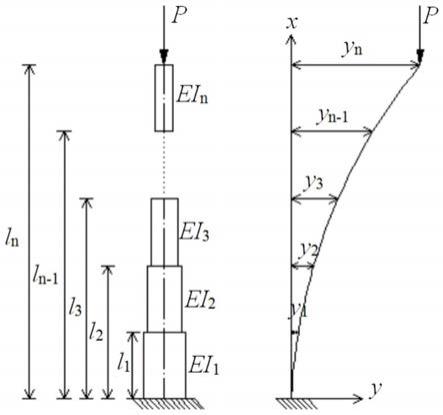
8.将伸缩臂架简化为n阶阶梯悬臂柱，绘制n阶阶梯悬臂柱的屈曲模型图和变形图，
设伸缩臂总长l＝l
n
，各阶悬臂柱的长度依次为l1，l2‑
l1，......l
n
‑1‑
l
n
‑2，l
n
‑
l
n
‑1；
9.s2、假设位移函数：
10.以屈曲模型图的底部固定端为原点取坐标轴，假设阶梯悬臂柱的位移函数为
[0011][0012]
其中，a
m
和b
m
为待定展开系数，h1＝
‑
x2/l+x3/l2，h2＝3x2/l2‑
2x3/l3，λ
m
＝mπ/l，对以上表达式，易于验证w(0)＝0,w'(0)＝0，即式(1)满足伸缩柱底部的固定边界条件；且顶部的弯曲位移(挠度)为w(l)＝a2，转角w'(l)＝a1；
[0013]
s3、基于位移函数求解屈曲受力模型：
[0014]
首先确定系统的能量，需分别求出弹性势能u、载荷p对应的势能u
p
,并得到总势能π，最后求解阶梯悬臂柱的屈曲特征值方程；
[0015]
s4、对屈曲受力模型的求解结果进行准确性验证；
[0016]
将s3得到的计算结果中的屈曲稳定系数与现有文献中的数据结果进行对比，比较误差值从而判断求解结果的准确性；
[0017]
s5、对屈曲受力模型的求解结果进行适用性验证；
[0018]
按照新型级数法对3
‑
5阶一端固定一端自由的阶梯柱在不同长度比和截面惯性矩比情况下进行分析并与现有文献数据结果中得出的精确解进行比较，判断其适用性。
[0019]
优选地，所述s3的具体操作方法包括以下步骤：
[0020]
式(1)右端除a1h1和a2h2外，余弦级数部分截取前8项，从而位移函数近似为：
[0021][0022]
其中，a
i
为未知系数，基底函数g
i
(x)为
[0023][0024]
弹性势能由各段柱的弹性势能组成为，具体为:
[0025][0026]
其中，e为阶梯柱材料的弹性模量,i
i
为第i段柱截面的惯性矩，w”(x)为w(x)对x的二阶导数。
[0027]
轴向载荷势能为：
[0028][0029]
其中，p为阶梯柱的末端轴向载荷，w'(x)为w(x)对x的一阶导数。
[0030]
系统的总势能：
[0031]
π＝u
e
+u
p
ꢀꢀꢀ
式(6)
[0032]
式(4)至式(6)中u
e
表示阶梯柱的弹性势能；u
p
表示柱的载荷势能；
[0033]
由瑞利—里兹法，总势能对式(1)中的各待定系数取极值，即：
[0034][0035]
由式(7)得到10个线性方程组，矩阵化得：
[0036]
(k
‑
pq)a＝0
ꢀꢀꢀ
式(8)
[0037]
式(8)中k为刚度矩阵，p为外荷载的代数值，q为载荷的系数矩阵，a是式(1)中新型级数中未知系数组成的列矩阵，即：
[0038]
a＝[a1,a2,a3,a4······
a
10
]
t
ꢀꢀꢀ
式(9)
[0039]
引入
[0040][0041][0042]
则刚度矩阵k为
[0043][0044]
类似地，几何矩阵q为
[0045][0046]
式(8)有非零解的条件是：
[0047]
|k
‑
pq|＝0
ꢀꢀꢀ
式(14)
[0048]
求解方程式(14)得到p的若干个根，这些根中的最小值就对应于阶梯柱的屈曲载荷。
[0049]
优选地，所述s4的具体操作方法为：
[0050]
引入屈曲稳定系数λ
[0051][0052]
其中，p为屈曲载荷，e为弹性模量，i1为第一段阶梯柱的截面惯性矩，对于一端固
定一端自由的二阶阶梯柱参数：ei2＝400n
·
m2,l＝10m，i2/i1取为0.4、0.6和0.8，l1/l取为0.2、0.3、0.4、0.5、0.6、0.7和0.8，将本文的屈曲稳定系数k与现有公开文献的计算结果作比较，计算误差，判断准确性。
[0053]
优选地，所述s5的具体操作方法为：
[0054]
引入计算长度系数μ2，且μ2满足：
[0055][0056]
其中，p为屈曲载荷，e为弹性模量，i为截面惯性矩，l为整段长度，μ1为边界有关的长度因数，对于一端固定一端自由的构件有μ1＝2，对于两端简支的构件有μ1＝1，
[0057]
按照新型级数法对3
‑
5阶一端固定一端自由的阶梯柱在不同长度比和截面惯性矩比情况下进行分析并与现有文献中得出的精确解进行比较，得到误差值。
[0058]
本发明与现有技术相比具有以下优点：
[0059]
1、本发明利用新型级数法对起重机伸缩臂架所属的悬臂型阶梯型柱的屈曲载荷进行研究。首先建立弯曲位移函数，在传统傅里叶级数的基础上增加了辅助多项式函数，并采用余弦差值项，解决了传统傅里叶级数在边界处存在导数不连续和收敛性差的问题。然后结合最小势能原理，利用瑞利
‑
里兹法进行求解得到屈曲载荷的表达式。最后利用数值计算软件进行模拟验证与已有文献的结果进行比较。该方法能获得任意边界条件下的阶梯型柱屈曲载荷，在精度、计算效率和收敛性方面有了一定的提高，同时也适用一般弹性边界条件。
[0060]
2、本发明解决了传统傅里叶级数在边界处存在导数不连续的问题，通过矩阵特征值问题求解，具有求解速度快、精度高、适合确定悬臂阶梯柱的特点。在多阶阶梯柱适用性方面，研究3
‑
5阶阶梯柱时，本文方法的误差较小，能够适合工程需要。
[0061]
下面结合附图和实施例对本发明作进一步详细说明。
附图说明
[0062]
图1是本发明中的阶梯柱屈曲模型及变形图。
[0063]
图2是本发明中的五阶阶梯柱示意图。
[0064]
图3是本发明中的八阶阶梯柱示意图。
具体实施方式
[0065]
本发明包括以下步骤：
[0066]
s1、建立阶梯柱的屈曲受力模型：
[0067]
将伸缩臂架简化为n阶阶梯悬臂柱，绘制n阶阶梯悬臂柱的屈曲模型图和变形图如图1所示，设伸缩臂总长l＝l
n
，各阶悬臂柱的长度依次为l1，l2‑
l1，......l
n
‑1‑
l
n
‑2，l
n
‑
l
n
‑1；
[0068]
s2、假设位移函数：
[0069]
以屈曲模型图的底部固定端为原点取坐标轴，假设阶梯悬臂柱的位移函数为
[0070][0071]
其中，a
m
和b
m
为待定展开系数，h1＝
‑
x2/l+x3/l2，h2＝3x2/l2‑
2x3/l3，λ
m
＝mπ/l，对以
上表达式，易于验证w(0)＝0,w'(0)＝0，即式(1)满足伸缩柱底部的固定边界条件；且顶部的弯曲位移(挠度)为w(l)＝a2，转角w'(l)＝a1；
[0072]
s3、基于位移函数求解屈曲受力模型：
[0073]
首先确定系统的能量，需分别求出弹性势能u、载荷p对应的势能u
p
,并得到总势能π，最后求解阶梯悬臂柱的屈曲特征值方程；
[0074]
s4、对屈曲受力模型的求解结果进行准确性验证；
[0075]
将s3得到的计算结果中的屈曲稳定系数与现有文献中的数据结果进行对比，比较误差值从而判断求解结果的准确性；
[0076]
s5、对屈曲受力模型的求解结果进行适用性验证；
[0077]
按照新型级数法对3
‑
5阶一端固定一端自由的阶梯柱在不同长度比和截面惯性矩比情况下进行分析并与现有文献数据结果中得出的精确解进行比较，判断其适用性。
[0078]
本实施例中，所述s3的具体操作方法包括以下步骤：
[0079]
式(1)右端除a1h1和a2h2外，余弦级数部分截取前8项，从而位移函数近似为：
[0080][0081]
其中，a
i
为未知系数，基底函数g
i
(x)为
[0082][0083]
弹性势能由各段柱的弹性势能组成为，具体为:
[0084][0085]
其中，e为阶梯柱材料的弹性模量,i
i
为第i段柱截面的惯性矩，w”(x)为w(x)对x的二阶导数。
[0086]
轴向载荷势能为：
[0087][0088]
其中，p为阶梯柱的末端轴向载荷，w'(x)为w(x)对x的一阶导数。
[0089]
系统的总势能：
[0090]
π＝u
e
+u
p
ꢀꢀꢀ
式(6)
[0091]
式(4)至式(6)中u
e
表示阶梯柱的弹性势能；u
p
表示柱的载荷势能；
[0092]
由瑞利—里兹法，总势能对式(1)中的各待定系数取极值，即：
[0093][0094]
由式(7)得到10个线性方程组，矩阵化得：
[0095]
(k
‑
pq)a＝0
ꢀꢀꢀ
式(8)
[0096]
式(8)中k为刚度矩阵，p为外荷载的代数值，q为载荷的系数矩阵，a是式(1)中新型级数中未知系数组成的列矩阵，即：
[0097]
a＝[a1,a2,a3,a4······
a
10
]
t
ꢀꢀꢀ
式(9)
[0098]
引入
[0099][0100][0101]
则刚度矩阵k为
[0102][0103]
类似地，几何矩阵q为
[0104][0105]
式(8)有非零解的条件是：
[0106]
|k
‑
pq|＝0
ꢀꢀꢀ
式(14)
[0107]
求解方程式(14)得到p的若干个根，这些根中的最小值就对应于阶梯柱的屈曲载荷。
[0108]
本实施例中，所述s4的具体操作方法为：
[0109]
引入屈曲稳定系数λ：
[0110][0111]
其中，p为屈曲载荷，e为弹性模量，i1为第一段阶梯柱的截面惯性矩，对于一端固定一端自由的二阶阶梯柱参数：ei2＝400n
·
m2,l＝10m，i2/i1取为0.4、0.6和0.8，l1/l取为0.2、0.3、0.4、0.5、0.6、0.7和0.8，将本文的屈曲稳定系数k与文献[何庭蕙.阶梯压杆的实用稳定计算[j].华南理工大学学报.1995，23(4):77
‑
86]提供的的计算结果作比较得到表1，由表1可知此方法与解析法最大的误差为3.0131％，证明本发明具有较好的精度。
[0112][0113]
表1 一端固定一端自由阶梯柱的屈曲稳定系数及误差
[0114]
本实施例中，所述s5的具体操作方法为：
[0115]
引入计算长度系数μ2，且μ2满足：
[0116][0117]
其中，p为屈曲载荷，e为弹性模量，i为截面惯性矩，l为整段长度，μ1为边界有关的长度因数，对于一端固定一端自由的构件有μ1＝2，对于两端简支的构件有μ1＝1，
[0118]
按照新型级数法对3
‑
5阶一端固定一端自由的阶梯柱在不同长度比和截面惯性矩比情况下进行分析并与文献[陆念力,都亮,兰朋.变截面阶梯压杆精确失稳特征方程及其稳定计算实用方法
‑
《塔式起重机设计规范》中阶梯柱计算长度的快捷计算及精度分析[j].建筑机械，2014(6)：76
‑
81.]中得出的精确解进行比较，得表2和表3。表2为3阶阶梯柱在一端固定一端自由的边界条件下的计算长度系数，可以看出计算长度系数在所列举的情况下最大误差为0.485％，精度较高；表3为4阶阶梯柱在一端固定一端自由的边界条件下的计算长度系数，在惯性矩比值较小的情况下，此方法误差较小。
[0119][0120]
表2 悬臂型3阶阶梯柱的计算长度系数μ2及误差
[0121][0122]
表3 悬臂型4阶阶梯柱的计算长度系数μ2及误差
[0123][0124]
表4 悬臂型5阶阶梯柱的计算长度系数μ2及误差
[0125]
使用该方法具体来研究5阶和8阶阶梯柱的实际失稳问题，具体内容如下：
[0126]
图2和图3分别给出了给出5阶阶梯柱和8阶阶梯柱的示意图。表5中给出了不同方法计算的五阶阶梯柱长度系数(也包含本文级数法与gb/t3811规范及数值结果)的比较，及与文献中数值解结果的相对误差。表6给出了八阶阶梯柱的计算长度系数及误差。
[0127]
如图2所示，5阶阶梯柱各段阶梯柱长度占比系数：α1＝0.24，α2＝0.43，α3＝0.62和α4＝0.81。截面惯性矩关系为i1＝β2i2，i2＝β3i3，i3＝β4i4，i4＝β5i5。
[0128]
表5中本文计算结果与gb/t3811规范结果的最大相对误差为0.8320％，误差较小。
[0129][0130][0131]
表5 五阶阶梯柱的计算长度系数及误差
[0132]
如图3所示八阶阶梯柱的各段长度占比系数为：α1＝0.16，α2＝0.28，α3＝0.40，α4＝0.52，α5＝0.64，α6＝0.76，α7＝0.88(α1,α2,
…
,α7对应于由底部向上的各段)。截面惯性矩
关系为i1＝β2i2，i2＝β3i3，i3＝β4i4，i4＝β5i5，i5＝β6i6，i6＝β7i7，i7＝β8i8。
[0133]
对应于屈曲载荷的计算长度系数如表6所示。
[0134][0135]
表6 八阶阶梯柱的计算长度系数及误差
[0136]
本实施例建立的n阶悬臂型阶梯柱的屈曲模型中，根据新型级数法假设位移函数表达式，利用最小势能原理建立能量表达式得到阶梯柱的特征方程，通过求解特征值获得模型的屈曲载荷。解决了传统傅里叶级数在边界处存在导数不连续的问题，具有求解速度快、精度高、适合确定悬臂阶梯柱的特点。
[0137]
在多阶阶梯柱适用性方面，研究3
‑
8阶阶梯柱时，本方法的误差较小，能够适合工程需要。
[0138]
以上所述，仅是本发明的较佳实施例，并非对本发明作任何限制。凡是根据发明技术实质对以上实施例所作的任何简单修改、变更以及等效变化，均仍属于本发明技术方案的保护范围内。