一种约束优化问题的线性收敛分布式离散时间优化算法的制作方法

本发明涉及多智能体系统的分布式优化技术领域，特别涉及一种约束优化问题的线性收敛分布式离散时间优化算法。

背景技术：

多智能体系统的分布式优化问题就是只通过局部计算和局部信息交换来寻找问题一致最优解。

目前，随着对大规模约束优化问题的重视日益增加，对各种优化问题的研究也已经取得了许多优秀的成果。在已有的研究成果中，不仅采用了离散时间算法，还采用了连续时间算法。近年来，设计分布式连续时间算法来处理优化问题变得越来越普遍，对于连续时间算法，分析其收敛性比较方便，但也存在一些不足，如难以精确比较不同算法的收敛速度，难以在有向图和时变图上解决相关的优化问题。因此，有必要采用离散时间算法来解决这些问题。

但是，现有的离散时间算法所用的步长都是衰减的，所以收敛速度慢。为了加快算法的收敛速度，一些技术提出了带有固定步长的算法，并证明了算法具有线性收敛速度。然而，这些方法只考虑了带权平衡有向图的情形，为了将这些结果推广到权重不平衡的情况，一些技术提出了解决算法。但这些算法只考虑了无约束优化问题，在现实中，优化问题往往是有约束的。而一些结果针对约束优化问题给出了带固定步长的离散时间算法，虽然算法采用了固定步长，但却不能达到线性收敛速度。因此，本发明的目的是设计具有线性收敛速度的离散时间算法，以解决具有闭凸集约束的分布式约束优化问题。

技术实现要素：

本发明主要考虑基于梯度追踪方法分别在有向平衡图和有向非平衡图上解决带有一个全局闭凸集约束的凸优化问题。

为了实现上述目的，本发明将通过如下的技术方案来实现：一种约束优化问题的线性收敛分布式离散时间优化算法，包括以下步骤：

步骤1：对凸优化问题模型和最优性条件给出具体描述；

步骤2：基于梯度追踪框架设计平衡图上的分布式离散时间算法；

步骤3：引入两个时间尺度对平衡图上的分布式离散时间算法进行收敛性分析；

步骤4：基于行随机矩阵关于特征值1的左特征向量估计方法，设计非平衡图上的分布式离散时间算法；

步骤5：使线性矩阵不等式相关矩阵的谱半径严格小于1，得到非平衡图上的分布式离散时间算法的严格收敛性。

具体如下：

1.凸优化问题和最优性条件：

本节考虑带有一个全局闭凸集约束的凸优化问题如下：

其中s是的决策变量。ω0是上的闭凸集。fi是节点i在上的局部凸目标函数。为了方便叙述。在后续的分析中假设n＝1，同时将在后面的注释5来讨论n>1时的情况。

为了后续分析方便，首先对优化问题的目标函数作一下假设。

假设1.对于所有的i＝1,2,...,n，函数fi都在上α-强凸且l-光滑。

容易得到若假设1成立，则全局目标函数f也α-强凸和l-光滑。接下来。在f的α-强凸和l-光滑性质下。将给出下面的重要引理。

引理1.令函数f是上α-强凸且l-光滑的函数，对于任意的成立

其中，u和v是中的任意两个向量，γ＝max{|1-ηα|,|1-ηl|}。

接下来将对凸优化问题(1)的最优性条件做一个具体的描述。

引理2.s^*是凸优化问题(1)的最优值点当且仅当对于任意的正实数ν0有

s^*是凸优化问题(1)的最优值点当且仅当

此外，对于任意的正实数ν0，凸优化问题(1)等价于

minv0f(s)s.t.s∈ω0,(3)

因此可以得到引理2中的结果。

在接下来的两个小节中。将分别在平衡图上和非平衡图上给出可以线性解决凸优化问题(1)的分布式离散时间算法。

2.平衡图上的分布式离散时间算法及收敛性分析：

在这一小节，考虑在强连通的平衡图上设计带有固定步长的分布式离散时间算法来线性解决凸优化问题(1)。算法设计为

其中xi(t)是节点i在t步的状态变量，yi(t)是节点i在t步对全局目标函数梯度的估计，矩阵a是设计为双随机矩阵的关联于给定强连通平衡图的邻接矩阵，η>0是一个固定步长，此外。初始值xi(0)可以任意选择，

令

则可以把算法(3)写成紧形式

x(t+1)＝pω(ax(t))-ηy(t)，(5a)

为了后续对于算法收敛性的分析，定义变量

由引理2可知s^*是凸优化问题(1)的最优解。

引理3.对于算法(4)和选定的初始值，下面等式成立：

证明：从迭代公式(4a)和的定义可直接得到(5a)成立。下面验证(5b)成立。由(4b)易知

从而有

亦即

这意味着变量不随着t的改变而改变，所以

又因为所以因此

从而得证。

接着将在假设1下，用变量和的线性组合来约束变量和从而构造出线性矩阵系统不等式。最终。通过选择合适的步长来使相关的系统不等式矩阵的谱半径严格小于1。从而得到所有节点的状态变量xi(t)线性收敛到x^*。

步骤1：放缩从迭代公式(4a)和在引理3中的不等式(5a)可得

进而得

存在正实数ρ′<1使得从而有

步骤2：放缩由(5a)可知

由假设1成立可得也是l-连续的。因此，若步长满足则可以通过引理1和(10)得到

步骤3：放缩从迭代公式(4b)和在引理3中得到的不等式(5b)

可知

也就意味着

对于||x(t+1)-x(t)||这一项，首先从迭代公式(4a)和x^*的定义可知

接着由于引理3中的(5b)成立，可以根据(14)得到

此外，注意到

可以得到

类似于(16)有

把(16)和(17)代入(15)即可得

进而把(18)代入(13)即可得到

接下来，通过上面得到的不等式(9)、(11)和(19)，在下面的引理中构造一个线性矩阵不等式系统来完成整个算法的收敛性证明。

引理4.令假设1成立，当算法(15)中的步长满足则对于算法中的更新变量满足线性矩阵不等式

其中

注1.从引理4可知，若ρ(g1′)<1，则和将以线性的速率衰减到0。而为了使ρ(g1′)<1，需要要求矩阵g1′的对角线元素都严格小于1，也就是需要2ρ′<1，这对于一般的强连通图而言是非常困难的。因此，若对于给定的强连通图，无法找到一个可以满足2ρ′<1的邻接矩阵a，则需要对算法(15)做一些改进。这就需要引入两个时间尺度，包括一个快时间尺度m和一个慢时间尺度t。进一步地，对于状态变量xi(t)的更新，首先需要选取初始值xi(m＝0,t)＝xi(t)来运行关于快时间尺度m的迭代其中m是一个满足的正整数。然后运行相关于慢时间尺度t的迭代从而由可得因此类似于步骤1中(8)的推导可以得到

其中0＜ρ＜1为一个常数。为了方便后面的叙述，对于给定的强连通图，不失一般性假设存在一个正常数ρ使得0＜2ρ′＝ρ＜1。相应地可以把引理4中的矩阵g1′调整为

定理1.令假设1成立且步长η满足则对于所有的i＝1,2，...,n，si(t)都以线性速率收敛到凸优化问题(1)的解。

证明：从引理4和注释1可知，只需证明当时，ρ(g1)＜1，即可完成证明。在假设1下，0＜α≤l。所以当时有1-ηα≥1-ηl>0，从而有γ＝1-ηα。接着通过直接的计算可以得到矩阵g1的特征多项式为

令p0(λ)＝λ²-2(ρ+ηl)λ+ρ(ρ+2ηl)-2ηl(2+ηl)，可以求得p0＝0的两个实根为由0＜ηl＜1可知从而有所以当时，

记则

其中第二个不等式的成立也是因为0＜ηl＜1。容易看出，p(λ)在区间(λ^*,+∞)上是严格增的，这就意味着p(λ)在区间(λ^*,+∞)上没有实根。此外，容易看出在定理的证明中需要不等式如果现有的ρ′不满足条件，可以再通过调整注释1中m的值来使上述不等式成立。因此，依旧可以假设ρ′满足证明中所需要的上述条件。又由可知所以矩阵g1所有的实特征值都严格小于1。从perron-frobenius定理可知，由于g1是一个非负矩阵，所以ρ(g1)等于g1的一个特征值，因此ρ(g1)＜1，从而得证。

注2.从上面的收敛性分析可以看出，注释1中使用的两个时间尺度是完成定理1证明的关键。在本节的结果中，对于每一步慢时间尺度t≥0下xi(t)的更新，相关的快时间尺度m的迭代只需要进行固定的m次。

3.非平衡图上的分布式离散时间算法及收敛性分析：

在本小节，将基于行随机矩阵关于特征值1的左特征向量估计方法，在强连通的有向非平衡图上设计分布式离散时间算法来解决凸优化问题(1)。

分布式的离散时间算法设计为

其中，a是设计为行随机矩阵的关于给定强连通有向非平衡图的邻接矩阵，zi(t)是节点i在第t步对矩阵a的关于特征值1的左特征向量的估计。此外，对于所有的i＝1,2,...,n，选取初始值xi(0)为任意的值，zi(0)＝nei，记由于aii>0且对于所有的j≠i有aij≥0，则在给定的初始值条件下，可得对于所有的t≥0，有因此，是定义良好的。

注3.令则(25b)可写作紧形式由zi(0)＝nei可得，其中π是随机矩阵a关于特征值1的左特征向量，满足1^tπ＝n。进而表明，对于所有的i＝1,2,...,n，有更进一步地，存在常数γ1>0和0＜β＜1使得由于矩阵a是非负矩阵且对角线元素严格正，则由给定初始值的形式可知，通过算法(25b)进行迭代的变量在任何有限的t时刻都是严格正的。此外，由于图强连通，所以存在一个正实数η0使得对于所有的i＝1，2，...，n，有πⁱ≥η0>0。因此由收敛到πⁱ可知，关于t一致有界且存在一个正实数z0使得对于任意的i＝1,2,...,n和t≥0，都有进而可以得到对于所有的i＝1,2,...,n，和关于t一致有界。为了方便叙述，对所有的i＝1,2,...,n，不失一般性地假设其中b≥1是一个正常数。

记则(25)可写作紧形式

x(t+1)＝pω(ax(t))-ηy(t),(26a)

为了完成算法(25)的收敛性分析，首先对上一小节的一些变量的定义做一些调整：

则在迭代公式(26)下，类似于引理3，对于新定义的变量可以得到引理5，由于证明和引理3的证明类似，引理5的证明就不再详细展开。

引理5.在给定的初始值条件下，可以得到

此外，为给后续的收敛性分析做准备，给出下面的引理6。

引理.6.令假设1成立，则有

其中，且

证明：由的定义可知

进一步地，在假设1下，由注释3中的结果可得

将(30)带入(29)可得(28)成立，从而得证。

接下来，和上一小节的收敛分析方法一样，用和的线性组合来放缩和从而构建线性矩阵不等式，最终选择合适的步长使线性系统不等式相关矩阵的谱半径严格小于1，来得到算法(25)的严格收敛性。

步骤1：放缩类似于上一小节的步骤1易得

步骤2：放缩由引理5中的(27a)可得

对于(32)右侧的最后一项，可以得到

其中，此外，由于则结合(27b)和(33)以及引理1可得

其中，

步骤3：放缩从(26c)和(27b)易得

进而根据引理6可得

此外，由迭代公式(26a)和x^*的定义可知

从而有

同时，类似于(33)的推导可以得到

从而结合(18)、(38)和(39)可以得到

因此，把(40)代入(36)可以得到

由上述分析中得到的(31)、(34)和(41)可以直接给出下面的引理7。

引理7.令假设1成立且步长满足则可以得到线性矩阵不等式

其中

且ρ＝2ρ′。

相应地根据引理7，给出本小节的主要定理。

定理2.令假设1成立且ω0是一个紧集。此外，令选取的步长η满足

则所有的si(t)都以线性速率收敛到凸优化问题(1)的最优解。

证明：类似于定理1的证明，由引理7可知，只需验证当步长满足条件(43)时，ρ(g)＜1，即可完成定理2的证明。由易知γ＝1-ηα，从而可得矩阵g的特征多项式为

同样地令p0(λ)＝λ²-2(ρ+ηbl)λ+ρ(ρ+2ηbl)-2ηbl(2+ηbl)，容易求得p0＝0的两个根为和由0＜ηbl＜1易知这就意味着从而当时，有

记则有

同样地，如若必要，可以采用注释1中给的方法来保证条件成立。进而可得，当时，成立，从而相似地可以得到ρ(g)＜1。

由于ω0是紧集，从注释3中的结果可知存在一个正常数m1使得||u(t)||≤m1β^t。记和ρ0＝max{ρ(g),β}+r0，其中r0一个严格正的常数且满足max{ρ(g),β}+r0＜1。则根据引理7可得

这就意味着||w(t+1)||线性衰减到0，从而得证。

注4.对于迭代中初始值zi(0)＝nei，n值可能不能为所有的节点所知，实际上算法(25)可以直接选择为zi(0)＝ei，同时，在证明的过程中只需调整一些系数即可完成证明，这一小节选择初始值zi(0)＝nei是为了使本小节的一些符号和上一小节的一些符号保持一致，对于算法的收敛性和收敛速率没有本质的影响。

注5.当n>1时，定义

以平衡图上的算法(4)为例，相应的紧形式为

x(t+1)＝pω(ax(t))-ηy(t),

这和紧形式(5)一样。同时，在收敛性分析中相应地替换标量x*、s*和为向量(x^*)^t、(s^*)^t和即可直接完成收敛性分析。此外，非平衡图上的算法(25)在n>1的情况下的收敛性分析也可以类似的完成。

注6.从上面的收敛性分析过程可以看出收敛性分析的关键是在特定情况下得到性质ρ(g1)＜1和ρ(g)＜1。可以看出引理1中的结果是保证矩阵g1和矩阵g的第三行第三列的元素γ严格小于1的关键，而γ＜1对于推导出性质ρ(g1)＜1和ρ(g)＜1也是至为关键的。

注7.若对于给定的平衡图，ρ′是不符合要求的。则为了得到在平衡图上的算法(4)的线性收敛性质，需要保证这就意味着关于快时间尺度的地带需要运行的次数满足此外，根据引理4可知，||x(t)-1x^*||≤∈0ρ^t(g1)，其中，则对于任意小的正实数∈>0，需要进行t1次迭代来使||x(t)-1x^*||≤∈，其中为一个正整数。类似地，对于涉及非平衡图的情况，需要进行t2次迭代，来使||x(t)-1x^*||≤∈，其中是一个正整数，是一个正整数，且

相对于现有技术，本发明的优点如下：本发明考虑了一个全局闭凸集约束的凸优化问题，分别在有向平衡图上和有向非平衡图上设计出了基于梯度追踪框架的分布式离散时间算法，同时算法被证明拥有线性收敛概率。本发明的一个重大创新是，找到了一个有效的闭凸集约束处理方法来和梯度追踪方法融合，率先在非平衡图上以带有线性收敛速率的分布式算法解决了带有约束的凸优化问题。

附图说明

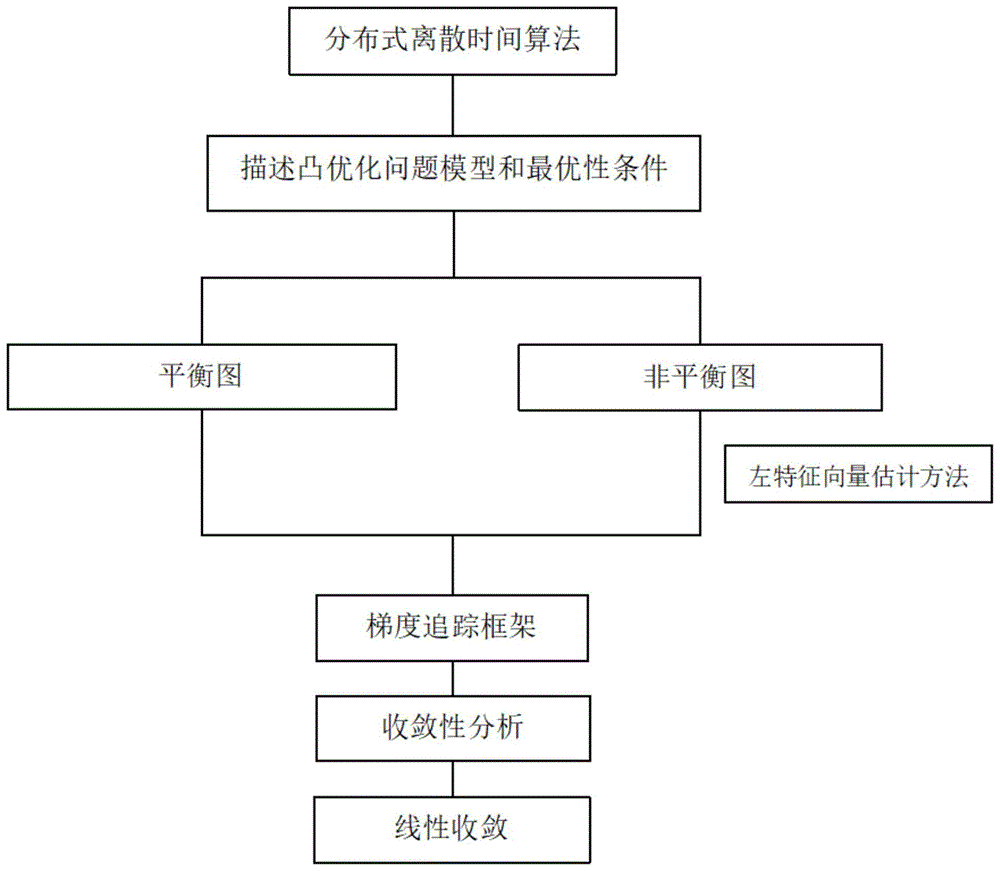
图1为算法结构示意图；

图2为包含十个节点的通讯图；

图3为通过算法(4)更新的向量si(t)的演化轨迹(-实线，-虚线)；

图4为通过算法(25)更新的向量si(t)的演化轨迹(-实线，-虚线)；

图5为通过平衡图上基于梯度下降方法的分布式离散时间算法更新向量si(t)的演化轨迹(-实线，-虚线)；

图6为通过非平衡图上基于梯度下降方法的分布式离散时间算法更新向量si(t)的演化轨迹(-实线，-虚线)。

具体实施方式

接下来根据附图并结合具体数值仿真实施方式来对本发明的技术方案作进一步阐述，并验证所设计算法的有效性。

考虑目标函数定义在的回归分析问题

其中，对于所有的i＝1,2,...,n和j＝1,2,...,r，且aij＝(-1)^(i+j)。此外，选择n＝10，r＝5以及σ＝10，十个节点的通讯图如图2所示，满足的闭凸集约束为s∈[-1,1]×[-1,1]。对于平衡图和非平衡图，相关的邻接矩阵a都定义为

从全局目标函数的形式可知，每个节点i负责的局部目标函数为

此外，分别选择步长η＝0.01和η＝0.001来进行算法(4)和(25)的数值迭代，且对应的十个节点状态si(t)的演化轨迹分别在图3和图4给出。想要解决带有一个全局闭凸集约束的凸优化问题，现有的方法分别在平衡图和非平衡图上设计了两种基于梯度下降方法的分布式离散时间算法。因此，为了将平衡图和非平衡图上基于梯度下降方法的分布式离散时间算法分别与本发明所设计的算法(4)和(25)进行比较，在相同设定下，选取合适的衰减步长来对基于梯度下降方法的分布式离散时间算法进行数值仿真，对应的十个节点状态si(t)的演化轨迹分别在图5和图6给出。可以看出，在算法(4)下，所有si(t)只需要大概70步即可完全收敛到最优值x^*＝(-0.0041，-0.0081)，然而在平衡图上基于梯度下降方法的分布式离散时间算法下，需要大于100步。同样可以看出，在算法(25)下，所有si(t)只需要大概120步即可完全收敛到最优值，然而在非平衡图上基于梯度下降方法的分布式离散时间算法下，需要大于500步。

在matlab中的具体实施方式为：

首先给出图3的对应代码

该段代码可以实现图3的绘制，分别在步长为η＝0.01和η＝0.001时对算法(4)进行数值迭代，并给出了十个节点状态si(t)的演化轨迹。

接下来给出图4的对应代码

该段代码可以实现图4的绘制，分别在步长为η＝0.01和η＝0.001时对算法(25)进行数值迭代，并给出了十个节点状态si(t)的演化轨迹。

接下来给出图5的对应代码

该段代码可以实现图5的绘制，选取合适的衰减步长来对平衡图上基于梯度下降方法的分布式离散时间算法进行数值仿真，分别在步长为η＝0.01和η＝0.001时对算法进行了数值迭代，并给出了十个节点状态si(t)的演化轨迹。

接下来给出图6的对应代码

该段代码可以实现图6的绘制，选取合适的衰减步长来对非平衡图上基于梯度下降方法的分布式离散时间算法进行数值仿真，分别在步长为η＝0.01和η＝0.001时对算法进行了数值迭代，并给出了十个节点状态si(t)的演化轨迹。

需要说明的是上述实施例，并非用来限定本发明的保护范围，在上述技术方案的基础上所作出的等同变换或替代均落入本发明权利要求所保护的范围。