一种采用非正交基的GMRES变型算法

一种采用非正交基的gmres变型算法
技术领域
1.本发明涉及科学与工程计算如计算电磁学等技术领域，尤其涉及一种采用非正交基的gmres变型算法。


背景技术：

2.在应用数学和科学工程计算领域，许多问题的数学模型都可以用线性方程组来描述。例如目标电磁特性仿真计算问题经由矩量法(mom)、有限元(fem)等数值算法离散化电磁场微积分方程即转化为了对矩阵方程的求解，又如流体力学中的navier
‑
stokes方程求解、量子色动力学(qcd)中的格点规范理论、惯性约束聚变(icf)中的三温能量方程求解、油藏数值模拟、地震反演模拟过程中的helmholtz偏微分方程求解等。
3.当系数矩阵为非对称情况时，广义最小残量法(gmres)特别是带重启的gmres即gmres(m)则是当今最常用的一类算法。gmres的运算量主要由矩阵向量乘积和向量正交化两部分构成，如何进一步降低其计算复杂度一直是一项颇具挑战性的工作。


技术实现要素：

4.为有效降低了计算复杂度，为此，本发明提出了一种采用非正交基的gmres变型算法，具体方案如下：
5.一种采用非正交基的gmres变型算法，包括以下步骤：
6.s1、选取初始解向量，计算初始残量，获取krylov子空间的第一维基向量；
7.s2、计算系数矩阵与第一维基向量的乘积，任意选取该乘积结果中的部分元素，并对第一维基向量作对应抽取，以二者的内积作为此向量在第一维基向量上的投影系数，由其残差向量确定krylov子空间的第二维基向量；
8.s3、计算系数矩阵与第二维基向量的乘积，再次通过抽取以及求解最小二乘问题获取新向量在由第一、第二维基向量张成的子空间上的一个斜投影向量，并由相应的残差向量确定第三维基向量，以此类推，直至获得第n维基向量；
9.s4、在每次生成新基向量的同时，根据投影系数向量构建并更新上hessenberg阵，通过求解其对应的矩阵方程的最小二乘问题，更新残量，直至残量为零或小于既定阈值。
10.具体地说，步骤s1具体为：
11.s11、建立线性方程组：
12.ax＝b
ꢀꢀ
(1)
13.设迭代初值为x0，则初始残量为r0＝b
‑
ax0；
14.s12、任意选取r0中部分元素记作r
0p
，krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第一维基向量q1由公式(2)确定；
15.q1＝r0/||r
0p
||2ꢀꢀ
(2)
16.对q1做和r
0p
一致的抽取时记作q
1p
，q
1p
为一单位化低维向量。
17.具体地说，步骤s2具体为：
18.s21、计算矩阵向量乘积aq1，并对相乘所得向量作与r
0p
一致的抽取记作(aq1)
p
，求解超定方程组
19.q
1p
α1＝(aq1)
p
ꢀꢀ
(3)的最小二乘解；
20.s22、由投影系数α1计算如下残差向量
21.δ1＝aq1‑
q1α1ꢀꢀ
(4)
22.s23、进而对δ1作和r
0p
一致的抽取记作δ
1p
，由
23.q2＝δ1/||δ
1p
||2ꢀꢀ
(5)
24.确定krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第二维基向量q2；记对q2作与r
0p
一致的抽取所得低维向量为q
2p
，q
2p
为单位化低维向量且q
2p
⊥
q
1p
。
25.具体地说，步骤s3具体为：
26.s31、计算矩阵向量乘积aq2，求解超定方程组
27.[q
1p q
2p
]α2＝(aq2)
p
ꢀꢀ
(6)的最小二乘解，其中(aq2)
p
由对aq2作和r
0p
一致的抽取所得；
[0028]
s32、再以α2作为投影系数向量，计算aq2的残差分量
[0029]
δ2＝aq2‑
[q
1 q2]α2ꢀꢀ
(7)
[0030]
s33、由
[0031]
q3＝δ2/||δ
2p
||2ꢀꢀ
(8)
[0032]
确定krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第三维基向量q3，其中δ
2p
表示由对δ2作和r
0p
一致的抽取所得低维向量；
[0033]
s34、以此类推，生成第四、第五、
……
、第n维基向量q4、q5、...、q
n
；对q3、q4、...、q
n
作与r
0p
一致的抽取分别记作q
3p
、q
4p
、...、q
np
，q
3p
、q
4p
、...、q
np
皆为单位化低维向量且q
np
⊥
...
⊥
q
3p
⊥
q
2p
⊥
q
1p
。
[0034]
具体地说，步骤s4具体为：
[0035]
s41、在步骤s1
‑
s3中的每次迭代生成新基向量的同时，利用α
i
及||δ
ip
||2(i＝1,2,...,n
‑
1)更新上hessenberg阵h，h
i
表示h的第i列，h
i
中的非零部分为[α
it
,||δ
ip
||2]
t
)，则有
[0036]
a[q1...q
i
‑1]＝[q1...q
i
]h (i＝1,2,...,n)
ꢀꢀ
(9)
[0037]
s42、通过计算
[0038]
hy
k
＝[||r
0p
||2,0,...,0]
t
(k＝1,2,...,n
‑
1)
ꢀꢀ
(10)的最小二乘解，更新原矩阵方程(1)的迭代解，即
[0039]
x
k
＝x0+[q1...q
k
]y
k
(k＝1,2,...,n
‑
1)
ꢀꢀ
(11)
[0040]
直至残量为零或小于既定阈值。
[0041]
本发明的有益效果在于：
[0042]
(1)与标准gmres算法在其arnoldi过程中生成标准正交基不同，本发明所构建的各维基向量之间一般不再具备正交性，但aq
i
‑
[q
1 q2...q
i
]α
i
与span{q1,q2,...,q
i
}之间仍具备一定的线性无关性。
[0043]
(2)在前述步骤中，每次迭代都令所抽取的元素位置与r
0p
保持一致(即每次都抽取相同的行)，这样做的好处是能保证{q
1p
,q
2p
,...,q
ip
}始终是一单位化正交阵，从而进一步
简化小规模最小二乘问题(如式(3)、(6))的求解，因此这种基函数生成过程亦可视为低维空间的施密特正交化，若不作此限制(即每次迭代都对aq
i
和[q
1 q2...q
i
]作不同的随机抽取)，算法依然有效，但每次小规模最小二乘计算都需作不同的qr分解，这将带来一定的额外运算量，因此基于该方法，本申请能够降低计算复杂度。
[0044]
(3)本发明中小规模超定方程组的求解实际上在计算出aq
i
的部分元素((aq
i
)
p
，亦即a
p
q
i
)后即可展开，故该类算法具备“天然”的并行能力(求出(aq
i
)
p
后便可并行计算aq
i
的剩余部分和[q
1p q
2p
...q
ip
]α
i
＝(aq
i
)
p
)。
[0045]
(4)本发明能有效降低已有gmres系列算法在向量正交化过程的运算量，且只需在传统gmres、gmres(m)、qgmres等方法的基础上添加“抽取”这一个环节即可，故代码改动量小、易于实现。同时，本发明中非正交基的实现过程也具备应用于其他krylov子空间迭代方法(特别是具有长递推关系的迭代法)的潜力。
附图说明
[0046]
图1为实施例1中残量误差变化曲线比较图。
[0047]
图2为实施例2中残量误差变化曲线比较图。
[0048]
图3为实施例3中圆锥形散射体示意图。
具体实施方式
[0049]
一种采用非正交基的gmres变型算法，包括以下步骤：
[0050]
s1、选取初始解向量，计算初始残量，获取krylov子空间的第一维基向量；具体步骤如下：
[0051]
s11、建立线性方程组：
[0052]
ax＝b
ꢀꢀ
(1)
[0053]
设迭代初值为x0，则初始残量为r0＝b
‑
ax0；
[0054]
s12、任意选取r0中部分元素记作r
0p
，krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第一维基向量q1即由公式(2)确定；
[0055]
q1＝r0/||r
0p
||2ꢀꢀ
(2)
[0056]
对q1做和r
0p
一致的抽取时记作q
1p
，q
1p
为一单位化低维向量。
[0057]
s2、计算系数矩阵与第一维基向量的乘积，任意选取该乘积结果中的部分元素，并对第一维基向量作对应抽取，以二者的内积作为此向量在第一维基向量上的投影系数，由其残差向量确定krylov子空间的第二维基向量；具体步骤如下：
[0058]
s21、计算矩阵向量乘积aq1，并对相乘所得向量作与r
0p
一致的抽取记作(aq1)
p
，求解超定方程组
[0059]
q
1p
α1＝(aq1)
p
ꢀꢀ
(3)
[0060]
的最小二乘解；
[0061]
s22、由投影系数α1计算如下残差向量
[0062]
δ1＝aq1‑
q1α1ꢀꢀ
(4)
[0063]
s23、进而对δ1作和r
0p
一致的抽取记作δ
1p
，由
[0064]
q2＝δ1/||δ
1p
||2ꢀꢀ
(5)
[0065]
确定krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第二维基向量q2；记对q2作与r
0p
一致的抽取所得低维向量为q
2p
，q
2p
为单位化低维向量且q
2p
⊥
q
1p
。
[0066]
s3、计算系数矩阵与第二维基向量的乘积，再次通过抽取以及求解最小二乘问题获取新向量在由第一、第二维基向量张成的子空间上的一个斜投影向量，并由相应的残差向量确定第三维基向量，以此类推，直至获得第n维基向量；具体步骤如下：
[0067]
s31、计算矩阵向量乘积aq2，求解超定方程组
[0068]
[q
1p q
2p
]α2＝(aq2)
p
ꢀꢀ
(6)
[0069]
的最小二乘解，其中(aq2)
p
由对aq2作和r
0p
一致的抽取所得；
[0070]
s32、再以α2作为投影系数向量，计算aq2的残差分量
[0071]
δ2＝aq2‑
[q
1 q2]α2ꢀꢀ
(7)
[0072]
s33、由
[0073]
q3＝δ2/||δ
2p
||2ꢀꢀ
(8)
[0074]
确定krylov子空间span{r0,ar0,a2r0,...,a
n
‑1r0}的第三维基向量q3，其中δ
2p
表示由对δ2作和r
0p
一致的抽取所得低维向量；
[0075]
s34、以此类推，生成第四、第五、
……
、第n维基向量q4、q5、...、q
n
；对q3、q4、...、q
n
作与r
0p
一致的抽取分别记作q
3p
、q
4p
、...、q
np
，q
3p
、q
4p
、...、q
np
皆为单位化低维向量且q
np
⊥
...
⊥
q
3p
⊥
q
2p
⊥
q
1p
。
[0076]
在生成第i+1维基向量的过程中，若aq
i
与q1,q2,...,q
i
线性无关，则在实施抽取后由针对小规模超定方程组(如式(3)、(6))所求得的最小二乘解可得到aq
i
在span{q1,q2,...,q
i
}中的一个斜投影，故aq
i
减去该投影所得向量与q1,q2,...,q
i
之间仍线性无关；若aq
i
与q1,q2,...,q
i
恰好线性相关，则[q
1 q2...q
i
]α
i
＝aq
i
和[q
1p q
2p
...q
ip
]α
i
＝(aq
i
)
p
为具有相同精确解的两个相容超定方程组，通过计算后者的最小二乘解即可获得此精确解，此时δ
i
＝0，h中将出现h
i+1,i
＝0，因此迭代结束，得x的精确解；若aq
i
与q1,q2,...,q
i
开始接近线性相关，则相比于不抽取的情况，[q
1p q
2p
...q
ip
]α
i
＝(aq
i
)
p
的最小二乘解α
i
作为一个局部最优解，将逼近aq
i
在span{q1,q2,...,q
i
}上的全局最优解，故aq
i
‑
[q
1 q2...q
i
]α
i
与span{q1,q2,...,q
i
}之间仍具备一定的线性无关性。
[0077]
s4、在每次生成新基向量的同时，根据投影系数向量构建并更新上hessenberg阵，通过求解其对应的矩阵方程的最小二乘问题，更新残量，直至残量为零或小于既定阈值，具体步骤为：
[0078]
s41、在步骤s1
‑
s3中的每次迭代生成新基向量的同时，利用α
i
及||δ
ip
||2(i＝1,2,...,n
‑
1)更新上hessenberg阵h，h
i
表示h的第i列，h
i
中的非零部分为[α
it
,||δ
ip
||2]
t
)，则有
[0079]
a[q1...q
i
‑1]＝[q1...q
i
]h (i＝1,2,...,n)
ꢀꢀ
(9)
[0080]
s42、通过计算
[0081]
hy
k
＝[||r
0p
||2,0,...,0]
t
(k＝1,2,...,n
‑
1)
ꢀꢀ
(10)的最小二乘解，更新原矩阵方程(1)的迭代解，即
[0082]
x
k
＝x0+[q1...q
k
]y
k
(k＝1,2,...,n
‑
1)
ꢀꢀ
(11)
[0083]
直至残量为零或小于既定阈值。
[0084]
为了实现上述方法啊，对应的软件代码如下：
[0085]
start:establish ax＝b and randomly select the positions“p”for extraction,then compute q1＝b/||b
p
||2.
[0086]
iterate:for j＝1,2,...,k,...,until satisfied do:
[0087]
h
i
,
j
＝<aq
jp
,q
ip
>,i＝1,2,...,j
[0088]
δ
j
＝aq
j
‑
∑
i
h
i
,
j
q
i
[0089]
h
j+1
,
j
＝||δ
jp
||2and q
j+1
＝δ
j
/h
j+1
,
j
[0090]
form the approximate solution:x
k
＝[q1...q
k
]y
k
,where y
k minimizes||[||b
p
||2,0,...,0]
t
‑
hy||2.
[0091]
在该伪代码基础上，只需通过限制迭代步数(即生成m维基向量后更新迭代初值和初始残量并重启算法)、采取截断策略(即仅构造aq
i
与最近生成的部分基向量之间的短递推关系式)，即可得到采用非正交基的gmres(m)、qgmres、qgmres(m)等系列变型算法。相比于已有gmres方法及其变型算法的迭代过程，新方法由于在计算每个hi,j时使用的都是两个低维向量，故具有更低的计算复杂度。
[0092]
以下通过三组数值实验验证本发明所提算法的可行性和高效性(程序运行环境为matlab 7.0，处理器intel(r)core(tm)i5
‑
6200u cpu@2.30ghz，内存8.00gb)。
[0093]
实施例1
[0094]
系数矩阵为sherman4矩阵、右端项为高斯随机向量的线性方程组，取零向量作为初始解向量，应用标准gmres和本发明所提算法(抽取行数设为200)分别进行求解。图1为两种方法的残量误差随迭代步数变化曲线比较图。由图1可见，二者具有完全一致的计算精度。进一步地，比较本发明中基于抽取生成新基向量的计算过程(例如式(6)～(8))与标准gmres中向量正交化部分的运算量，易知在每步迭代时其比值皆约为200/1104≈18.1％，可见新方法在维持了计算精度的同时，能有效降低生成krylov子空间基向量的计算复杂度。
[0095]
实施例2
[0096]
引入截断策略，考察以orsreg_1为系数矩阵、右端项仍为随机向量的矩阵方程，比较本发明方法(以抽取比例设为1/3为例，即抽取行数为2205/3＝735)与qgmres在采用相同截断范围(以取最近生成的50维基向量作为截断范围为例)时的残量误差变化情况，结果如图2所示。由图2可见，在截断“长度”相等的情况下，本发明具备和qgmres一致的计算精度(而其在本例中的基向量构造过程所消耗运算量仅为qgmres的33.3％)。
[0097]
实施例3
[0098]
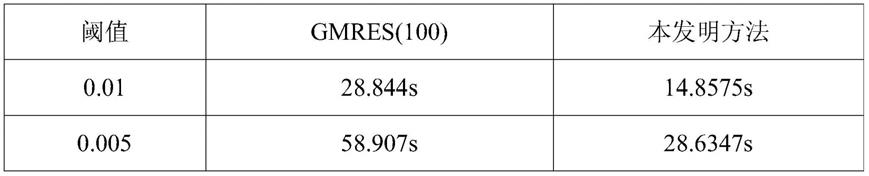
如图3所示，一pec圆锥体在频率为3ghz的入射波照射下的电磁散射问题。采用mom离散电场积分方程(efie)对该问题进行求解，选取rwg基函数对散射目标表面感应电流进行建模(基函数个数n＝4424)。在本算例中，以gmres(m)作为比较对象，每次循环的迭代步数设为m＝100，相同的重启策略亦用于本发明方法。同时，在两种方法中都使用多层快速多极子(mlfmm)技术对矩阵向量乘积运算进行加速。比较在取不同误差阈值时gmres(100)与本发明(以抽取比例设为1/4为例，即抽取行数为n/4＝1106)的计算时间，结果如表1所示。由表1可见，在采取相同重启策略的情况下，本发明方法在达到同等计算精度时所需的运算时间较gmres(m)显著减少。
[0099][0100][0101]
以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都应涵盖在本发明的保护范围之内。