一种基于模态划分的有源型MMC时域解析建模方法

一种基于模态划分的有源型mmc时域解析建模方法
技术领域
1.本发明涉及柔性直流输电技术和储能及节能技术领域，具体涉及一种基于模态划分的有源型mmc时域解析建模方法。


背景技术：

2.新能源存在诸多问题，比如太阳能、风能受到天气变化、辐射强度变化等因素的影响，具有波动性、间歇性等特点，新能源发电出力的间歇性和不确定性会引起并网功率波动，对电网平稳运行和电能质量造成不利影响，大规模并网运行将给电网带来安全隐患。
3.针对上述挑战，引入储能技术成为一种有效的解决方案。所谓储能技术，就是将电能转变成其他形式的能量存储起来，并在需要的时候释放电能的技术。储能技术将会在很大程度上解决新能源发电的波动性、间歇性等问题。解决传统电网结构和运行技术在接纳大规模新能源电力并网时难以满足能量多向流动、功率流的主动调控等系统需求的问题。利用储能技术安全、高效地消纳高比例新能源发电受到广泛关注。其中，有源型mmc因具备运行效率高、外送能力强、模块化程度高和调节储能容量灵活等显著优势，已成为最具潜力的储能方案之一。计算有源型mmc电容电压、电容电流、储能电流时域解析表达式，对分析相关电气量影响因素、设备选型、参数优化等工作具有重要意义，因此需搭建基于模态划分的有源型mmc时域解析模型。


技术实现要素：

4.本发明为解决上述现有大规模新能源并网的挑战和问题，提供一种基于模态划分的有源型mmc时域解析建模方法。
5.为了实现上述发明目的，本发明采取如下技术方案：
6.1.基于模态划分的有源型mmc时域解析模型。其特征在于，包括：
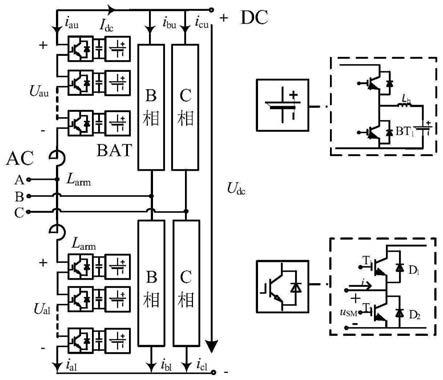
7.有源型mmc在本质上仍为三相电压源换流器，其子模块拓扑结构为电池储能单元经双向dc
‑
dc变换器并联于半桥子模块电容侧，是mmc的一个引申结构。有源型mmc系统属于三端口变流器，同时连接交流端、直流端和电池储能端。
8.根据功率守恒原理，流入三端口变流器的功率和为零，因此控制三端中的两端功率，即可控制变流器三端的功率，增加了控制功率的自由度。有源型mmc可分为直流侧功率控制，交流侧功率控制和储能电池充放电的功率控制，本发明采用同时控制交流侧功率和储能侧功率的控制策略。有源型mmc交流侧功率控制采用经典的内外环功率解耦控制，每个子模块中增加一个双向dc
‑
dc变换器，因此在控制上增加一个自由度。储能侧可设定不同的功率参考值单独控制每个储能模块充放电。当储能模块处于充电状态时，导通t4和d3，与滤波电感l
b
构成boost电路，使双向dc
‑
dc变换器工作在升压模式。当储能模块处于放电状态，导通双向dc
‑
dc变换器中的t3和d4，与滤波电感l
b
构成buck电路，使双向dc
‑
dc变换器工作在降压模式。有源型mmc中的储能模块采用shepherd模型，将其充放电简化为一个可逆过程，将其放电过程化分为三个区：指数区、额定工作区和深度放电区。额定状态下放电电压数值
为额定电压e
b
。
9.2.基于模态划分的有源型mmc时域解析模型的建模方法。其特征在于，该模型建立包括以下步骤：
10.最后根据子模块拓扑结构、kcl和kvl列写微分方程组，推导出有源型mmc电容电压、电容电流和储能电流的时域解析表达式，建立基于模态划分的有源型mmc时域解析模型。
11.步骤1：根据有源型mmc子模块拓扑、电池储能充放电机理和半桥子模块igbt状态，分析其不同工作状态下的工作模式。
12.步骤2：根据有源型mmc等效电路和数学原理，推导出上、下桥臂电压时域解析表达式和考虑二次谐波环流的上、下桥臂电流数学时域解析表达式。
13.步骤3：引入开关函数模型，建立桥臂电流与流入子模块电流的关系，引入平均值法，建立储能电流与双向dc
‑
dc变换器输出电流的关系。
14.步骤4：根据有源型mmc的不同工作模式和基尔霍夫定律，根据储能等效模型和电容器特性，列写微分方程组，推导出有源型mmc的电容电压、电容电流和储能电流的时域解析表达式，建立基于模态划分的有源型mmc时域解析模型。
15.本发明提供的有源型mmc时域解析模型建模方法填补了适用于有源型mmc时域解析建模方法的技术空白，能够针对子模块拓扑为电池储能单元经dc
‑
dc变换器并联在电容侧的有源型mmc的相关电气量影响因素分析，为抑制电容电压波动和减小电流中谐波含量，对设备选型、参数优化提供理论依据。
附图说明
16.图1是本发明实施例中有源型mmc时域解析模型建模方法流程图；
17.图2是本发明实施例中有源型mmc拓扑结构图；
18.图3是本发明实施例中有源型mmc控制策略图；
19.图4是本发明实施例中有源型mmc子模块拓扑结构图；
20.图5是本发明实施例中有源型mmc工作状态和工作模式图；
具体实施方式
21.附图仅用于示例性说明，不能理解为对本专利的限制；为了更好说明本实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；
22.对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。下面结合附图和实施例对本发明的技术方案做进一步的说明。
23.本发明实施提供了一种有源型mmc时域解析模型建模方法，具体流程图如图1所示，具体过程如下：
24.s101：根据有源型mmc子模块拓扑、电池储能充放电机理和半桥子模块igbt状态，分析其不同工作状态下的工作模式。
25.s102：根据有源型mmc等效电路和数学原理，推导出上、下桥臂电压时域解析表达式和考虑二次谐波环流的上、下桥臂电流数学时域解析表达式。
26.s103：引入开关函数模型，建立桥臂电流与流入子模块电流的关系，引入平均值
法，建立储能电流与双向dc
‑
dc变换器输出电流的关系。
27.s104：根据有源型mmc的不同工作模式和基尔霍夫定律，根据储能等效模型和电容器特性，列写微分方程组，推导出有源型mmc的电容电压、电容电流和储能电流的时域解析表达式，建立基于模态划分的有源型mmc时域解析模型。
28.1.上述的s101中，根据有源型mmc子模块拓扑、电池储能充放电机理和半桥子模块igbt状态，分析其不同工作状态下的工作模式，如图4和图5所示。
29.有源型mmc在本质上仍为三相电压源换流器，其子模块拓扑结构为电池储能单元经双向dc
‑
dc变换器并联于半桥子模块电容侧，是mmc的一个引申结构，如图2所示。有源型mmc系统属于三端口变流器，同时连接交流端、直流端和电池储能端。
30.p
sref
‑
p
bref
＝p
dcref
ꢀꢀ
(1)
31.其中，p
sref
为交流侧功率，p
dcref
为直流侧功率，p
bref
为储能侧功率。
32.根据功率守恒原理，流入三端口变流器的功率和为零，因此控制三端中的两端功率，即可控制变流器三端的功率，增加了控制功率的自由度。有源型mmc可分为直流侧功率控制，交流侧功率控制和储能电池充放电的功率控制，本发明采用同时控制交流侧功率和储能侧功率的控制策略。有源型mmc交流侧功率控制采用经典的内外环功率解耦控制，每个子模块中增加一个双向dc
‑
dc变换器，因此在控制上增加一个自由度。储能侧可设定不同的功率参考值单独控制每个储能模块充放电。当储能模块处于充电状态时，导通t4和d3，与滤波电感l
b
构成boost电路，使双向dc
‑
dc变换器工作在升压模式。当储能模块处于放电状态，导通双向dc
‑
dc变换器中的t3和d4，与滤波电感l
b
构成buck电路，使双向dc
‑
dc变换器工作在降压模式。有源型mmc中的储能模块采用shepherd模型，将其充放电简化为一个可逆过程，将其放电过程化分为三个区：指数区、额定工作区和深度放电区。额定状态下放电电压数值为额定电压e
b
。
33.2.上述的s102中，根据有源型mmc等效电路和数学原理，推导出上、下桥臂电压时域解析表达式和考虑二次谐波环流的上、下桥臂电流数学时域解析表达式。
34.功率以流入换流站为正方向，在忽略桥臂功率损耗时，交流侧、直流侧和储能侧功率守恒，得到
35.p
sref
‑
p
bref
＝p
dcref
ꢀꢀ
(2)
[0036][0037][0038]
上、下桥臂电压u
au
、u
al
可表示为
[0039][0040]
考虑二次谐波循环电流的上、下桥臂电流i
au
、i
al
可表示为
[0041][0042][0043]
其中，p
sref
为交流侧功率，p
dcref
为直流侧功率，p
bref
为储能侧功率，u
dc
为直流电压值，u
m
为交流电压幅值，i
m
为基频电流的幅值，u
b
为电池储能单元端口电压，i
b
为储能电流，为功率因数角，为二次谐波循环电流的初始相位角，为a相上桥臂电压初始相角，i2为二次谐波循环电流的幅值，ω为基角频率，m为调制比。
[0044]
3.上述的s103中，引入开关函数模型，建立桥臂电流与流入子模块电流的关系，引入平均值法，建立储能电流与双向dc
‑
dc变换器输出电流的关系。
[0045]
当子模块投入时u
sm
＝u
c
，s＝1，当子模块切除时u
sm
＝0，s＝0。a相上桥臂第i个子模块的端口电压可表示为
[0046]
u
sm,au_i
＝s
au_i
·
u
c,au_i
ꢀꢀ
(8)
[0047]
其中，u
sm
为子模块端口电压，u
c
为子模块电容电压，s
au
_
i
为a相上桥臂第i个子模块的开关函数。平均开关函数表示桥臂中子模块的平均投入比，a相上桥臂平均开关函数为
[0048][0049]
由a相上桥臂电压和子模块电容电压关系得
[0050][0051]
将式(4)代入式(9)，可得
[0052][0053]
双向dc
‑
dc变换器中的igbt t3和t4有着较高的频率，是工频的60倍。因此将t3和t4作平均值等效，定义占空比为α。由图3的控制策略，易知
[0054][0055]
根据双向dc
‑
dc变换器pwm控制原理可得
[0056][0057]
根据调制波和三角载波比例关系可得
[0058]
α＝1
‑
d
ꢀꢀ
(14)
[0059]
其中，k
p1
、k
p2
为控制器比例系数，k
s1
、k
s2
为积分系数，p
bat_ref
为单个子模块储能功率参考值，p
bat
为单个子模块储能功率实际值，i
biref
为单个子模块储能电流参考值，i
bi
为单个子模块储能电流实际值，d为pwm调制波。
[0060]
可得到有源型mmc的电容电流、电容电流和储能电流满足如下关系：
[0061]
i
c
‑
αi
b
＝s
au
·
i
au
ꢀꢀ
(15)
[0062]
4.上述的s104中，最终有源型mmc数学模型由下式确定。
[0063]
根据有源型mmc的不同工作模式和基尔霍夫定律，根据储能等效模型和电容器特性，列写微分方程组，推导出有源型mmc的电容电压、电容电流和储能电流的时域解析表达式，建立基于模态划分的有源型mmc时域解析模型。
[0064]
调制策略充分发挥作用，各子模块电容电压u
c
一致，根据电容电压u
c
、电感电压u
l
、电阻电压u
r
、电池储能单元电压e
b
可列写出kvl方程。
[0065][0066]
电容电压和电容电流关系式为
[0067][0068]
将式(14)和式(16)代入式(15)，可得
[0069][0070]
求解线性微分方程得到有源型mmc电容电压解析表达式u
c
。
[0071][0072][0073][0074]
[0075][0076][0077][0078][0079]
[0080][0081][0082][0083]
其中，c1和c2为常数，a
*i
、b
*i
(i＝1～10)为系数参数。有源型mmc在正常运行时，子模块电容电压因保持恒定，但因无功功率和储能功率在一个周期对换流阀充放电的能量会引起子模块电容电压波动。
[0084]
根据电容电压与电容电流关系式(16)和式(15)，可推导得到储能电流解析表达式i
b
。
[0085][0086]
[0087][0088][0089][0090][0091][0092]
根据kcl方程式(14)，可推导得到电容电流解析表达式i
c
。
[0093]
[0094][0095][0096][0097][0098][0099][0100]
式(18)、(29)、(35)组成了有源型mmc用开关函数表示的子模块时域解析模型。上述所有时域解析式构成了基于模态划分的有源型mmc时域解析模型。
[0101]
本领域内的技术人员应明白，本技术的实施例可提供为方法、系统、或计算机程序产品。因此，本技术可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本技术可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd
‑
rom、光学存储器等)上实施的计算机程序产品的形式。
[0102]
本技术是参照根据本技术实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。
[0103]
这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。
[0104]
这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。
[0105]
最后应当说明的是：以上实施例仅用以说明本发明的技术方案而非对其限制，所属领域的普通技术人员参照上述实施例依然可以对本发明的具体实施方式进行修改或者等同替换，这些未脱离本发明精神和范围的任何修改或者等同替换，均在申请待批的本发明的权利要求保护范围之内。