一种基于连通性空间权重矩阵的区域交通安全评价方法与流程

本发明属于交通安全技术领域，特别涉及一种基于连通性空间权重矩阵的区域交通安全评价方法。

背景技术：

道路交通安全是关系到人类健康与发展的世界性问题，近年来，以人口普查区、交通分析小区(Traffic Analysis Zone，TAZ)等为基础的区域交通安全问题开始得到社会的普遍关注，区域内各类事故的特征及事故的影响因素及伤害机理亟需深入研究，可以通过考量各类事故与事故影响因素之间的关系，更全面地了解区域安全水平与事故隐患，以及采取相应的措施预防事故发生，保障生命财产安全与道路畅通。区域事故风险预测模型中通常以事故数作为因变量。由于事故数的非负性、随机性与离散性，通常采用计数模型用于事故数的预测。计数模型是一种概率回归模型，包括传统的泊松模型、泊松对数正态模型以及负二项分布模型等，传统的事故风险预测模型假设事故数的分布在空间上是相互独立的，然而，相邻区域在土地利用形态、道路设计要素和社会经济等方面都具有相似性，对事故空间相关性的忽略将影响模型估计的准确性和鲁棒性。为克服传统事故风险预测模型的局限性，空间统计分析方法，尤其是基于完全贝叶斯方法的考虑空间相关性的贝叶斯条件自回归(Conditional Autoregressive，CAR)模型逐渐成为交通安全分析与评价领域的一个前沿研究方向。

在度量空间相关性时，需要用空间权重矩阵来衡量空间对象的相互邻接关系，这是与传统统计建模的重要区别之一，也是进行空间统计分析的前提和基础。如何构建空间权重矩阵是空间统计建模的一项难题。在区域交通安全评价中，使用最多的是0‐1一阶邻接矩阵，即如果两个区域有公共边界，则两者的权重被赋值为1，否则为0，其次使用较多的是基于几何质心距离的空间权重矩阵。区域交通安全评价中，单纯依靠邻接关系或距离核函数并不能充分地表示区域的相互关系，较合理的空间权重矩阵是在考虑地理维度的基础上，还要考虑其他方面的影响，如交通量、道路容量和出行方式等，因此目前空间权重矩阵构建的局限性仍然是引起区域交通安全评价精准度不高的技术问题。

技术实现要素：

本发明的目的是提供一种基于连通性空间权重矩阵的区域交通安全评价方法，其特征在于，包括以下步骤：

步骤一：采集区域交通安全分析的相关数据，包括事故数据、交通流量、道路设计参数、交通控制与管理要素以及影响区域交通安全的土地利用形态、时间分布的因素，建立相应的区域交通安全分析数据库，进行数据预处理；

步骤二：建立以交通分析小区为基本单元的贝叶斯条件自回归模型作为区域事故风险预测模型，对于交通分析小区TAZ_i(TAZ为Traffic Analysis Zone的简写，区域)，其一段时间内实际发生的事故数为y_i服从泊松分布，则

y_i～Poisson(e_iλ_i)

其中，λ_i为事故数的预测值，e_i为曝光量；同时对事故数的预测值建模为

其中，X_i为可能影响事故发生的因素，β₀为常数项，模型参数β＝(β₁,...β_p)′为影响因素相应的影响系数，θ_i为无结构的随机效应，服从正态分布φ_i为空间随机效应，服从条件自回归的先验分布，即

其中，为θ_i的精度，为空间随机效应的期望，为空间随机效应的精度，ω_ij为TAZ_i与TAZ_j的邻接关系，为精度系数先验；

步骤三：以区域间所含的路径条数对网络连通度进行标识，构建空间权重矩阵：

(1)交通状态网络，将TAZ(区域)及其连接路径所构成的交通状态网络定义为不含环的无向加权图，记作G＝(V,E)，其中V为网络的顶点集，指区域的有限集合，V＝{TAZ₁,TAZ₂,…,TAZ_n}；E为网络的边集，指区域间的连接路径，E＝{e_ij}，e_ij为区域TAZ_i与TAZ_j之间的路径，TAZ_i,TAZ_j∈V，用两个区域的几何质心连线表示；Q(e_ij)为相应边的权值，表示区域i与j的交通容量，用连接两个区域的实际路径条数表示；

(2)交通状态网络连通度的计算。设区域i与j的几何质心距离为C(e_ij)，相应的交通容量为Q(e_ij)，在不考虑其他因素的影响下，连通度定义为

ω_ij＝Q^α(e_ij)/C^β(e_ij)(i≠j)

其中，α、β分别表示交通容量和路径里程的权重系数。

(3)基于连通性的空间权重矩阵构建，根据区域间的连通度，可以得到网络的权重矩阵W＝(ω_ij)_n×n即

其中，当W＝ω_ij时，表示区域i与j之间存在直接相连的路径；当W＝0时，表示区域i与j之间没有直接相连的路径，或区域i与j是同一个节点，即i＝j；

步骤四：基于连通性空间权重矩阵的区域事故风险预测模型进行模型参数估计，得出模型参数β的均值、标准差、置信区间和显著水平，筛选对区域事故发生影响显著的因素，这些因素称为显著因素，分析显著因素对事故数y_i的影响，推出安全改进措施对策与建议。

所述步骤一进行数据预处理包括：

(1)数据清洗：填写缺失值、光滑噪声数据、识别或删除离群点；

(2)数据集成：将多个数据源中的数据结合起来并统一存储；

(3)数据变换：将原始数据转换成为适合模型参数估计的形式。

所述空间权重矩阵具有如下性质：

(1)W为对称矩阵；

(2)G为无环图，则W中第i行或列的元素之和等于顶点区域i的度；

(3)两图G₁和G₂同构的充分必要条件为存在可逆矩阵C，使得

W(G₁)＝C^TW(G₂)C

如果连接两个区域的路径越多，那么这两个区域相互流动和渗透的可能性就会越高，两个区域的联系程度就会越紧密。

所述可逆矩阵C的每一列是矩阵W(G₂)的对应特征值的线性无关的特征向量。

本发明的有益效果是：本发明提出的基于连通性空间权重矩阵的区域交通安全评价方法，首先通过数据调查采集区域交通安全评价的相关数据，然后建立以交通分析小区为基本单元的贝叶斯条件自回归模型作为区域事故风险预测模型和构建以区域间所含的路径条数对网络连通度进行标识的空间权重矩阵，最后进行模型参数估计，克服了传统事故风险预测模型没有考虑空间相关性而造成模型精准度不高的问题，基于连通性的空间权重矩阵既考虑了地理维度的影响，又考虑了区域间实际的交通联系，具有较好的数据拟合度和数据适应性，可以挖掘更多与事故发生相关的显著因素，有效指导实践应用。

附图说明

图1为区域交通安全评价方法流程图。

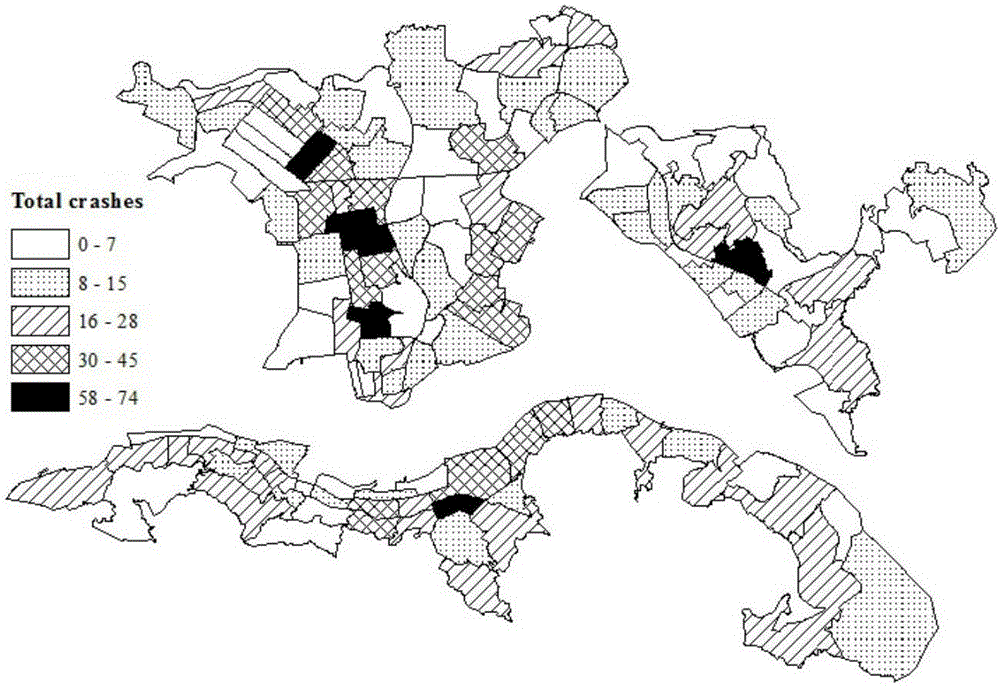
图2为2011年香港特别行政区131个交通分析小区行人交通事故分布图。

具体实施方式

本发明提供一种基于连通性空间权重矩阵的区域交通安全评价方法，下面结合附图和具体实施方式，进一步阐明本发明。

如图1所示，基于连通性空间权重矩阵的区域交通安全评价方法，包括以下步骤，

第一步，采集区域交通安全分析的相关数据，包括事故数据、交通流量、道路设计参数、交通控制与管理要素以及其它可能影响区域交通安全的土地利用形态、时间分布等因素，建立相应的区域交通安全分析数据库，进行数据预处理；

第二步，建立以交通分析小区为基本单元的贝叶斯条件自回归模型作为区域事故风险预测模型，对于交通分析小区i，即Traffic Analysis Zone，简写为TAZ_i，其一段时间内实际发生的事故数为y_i服从泊松分布，则

y_i～Poisson(e_iλ_i) (1)

其中，λ_i为事故数的预测值，e_i为曝光量；同时对事故数的预测值建模为

其中，X_i为可能影响事故发生的因素，β₀为常数项，模型参数β＝(β₁,...β_p)′为影响因素相应的影响系数，θ_i为无结构的随机效应，服从正态分布φ_i为空间随机效应，服从条件自回归的先验分布，即

其中，为θ_i的精度，为空间随机效应的期望，为空间随机效应的精度，ω_ij为TAZ_i与TAZ_j的邻近关系，为精度系数先验。

第三步，以区域间所含的路径条数对网络连通度进行标识，构建空间权重矩阵。

1.交通状态网络，将区域(TAZ)及其连接路径所构成的交通状态网络定义为不含环的无向加权图，记作G＝(V,E)，其中V为网络的顶点集，指区域的有限集合，V＝{TAZ₁,TAZ₂,…,TAZ_n}；E为网络的边集，指区域间的连接路径，E＝{e_ij}，e_ij表示区域TAZ_i与TAZ_j之间的路径，TAZ_i,TAZ_j∈V，用两个区域的几何质心连线表示；Q(e_ij)为相应边的权值，表示区域i与j的交通容量，用连接两个区域的实际路径条数表示；

2.交通状态网络连通度的计算，设区域i与j的几何质心距离为C(e_ij)，相应的交通容量为Q(e_ij)。在不考虑其他因素的影响下，连通度可以定义为

ω_ij＝Q^α(e_ij)/Cγ(e_ij)(i≠j) (6)

其中，α、γ分别表示交通容量和路径里程的权重系数，本实施例可令α＝γ＝1。

3.基于连通性的空间权重矩阵构建。根据区域间的连通度，可以得到网络的权重矩阵W＝(ω_ij)_n×n即

其中，当W＝ω_ij时，表示区域i与j之间存在直接相连的路径；当W＝0时，表示区域i与j之间没有直接相连的路径，或区域i与j是同一个节点，即i＝j。

根据空间权重矩阵的定义，可得如下若干性质：

(1)W为对称矩阵；

(2)G为无环图，则W中第i行(列)的元素之和等于顶点区域i的度；

(3)两图G₁和G₂同构的充分必要条件为存在可逆矩阵C，使得

W(G₁)＝C^TW(G₂)C (8)

如果连接两个区域的路径越多，那么这两个区域相互流动和渗透的可能性就会越高，两个区域的联系程度就会越紧密。

第四步，基于连通性空间权重矩阵的区域事故风险预测模型进行模型参数估计，得出模型参数β的均值、标准差、置信区间和显著水平，筛选对区域事故发生影响显著的因素，这些因素称为显著因素，分析显著因素对事故数y_i的影响，推出安全改进措施对策与建议。

如图2所示，本实施例选择2011年香港特别行政区131个交通分析小区的行人事故数据为研究对象。采集了六种类型的数据，包括行人事故数据、道路网络设计要素、车辆特征参数、人口社会经济指标、土地利用形态以及时间分布，进行数据预处理。共得到768条数据，特征描述如表1所示。

表1模型数据特征描述情况

建立以交通分析小区为基本单元的贝叶斯条件自回归模型作为区域事故风险预测模型并构建以区域间所含的路径条数对网络连通度进行标识的空间权重矩阵。

然后基于连通性空间权重矩阵的区域事故风险预测模型进行模型参数估计，估计结果见表2，得到模型参数的均值、标准差、置信区间和显著水平。

表2基于连通性空间权重矩阵的区域事故风险预测模型的模型参数估计结果

*表示95％水平显著

用传统的没有考虑空间相关性的泊松对数正态模型、基于0‐1一阶邻接矩阵的贝叶斯条件自回归模型以及基于几何质心距离空间权重矩阵的贝叶斯条件自回归模型根据相同的数据集进行计算，并将所得结果与基于连通性的贝叶斯条件自回归模型估计结果进行对比，如表3所示。

表3模型估计结果对比

上表中DIC表示偏差信息度，越小越好。

贝叶斯条件自回归模型克服了传统事故风险预测模型没有考虑空间相关性而造成模型精准度不高的问题，基于连通性的空间权重矩阵的区域事故风险预测模型具有较好的数据拟合度和数据适应性，可以挖掘更多与事故发生相关的显著因素，有效指导实践应用。