基于APDE‑RBF神经网络的网络安全态势预测方法与流程

本发明属于网络安全技术领域，特别涉及一种基于吸引子传播差分进化算法的径向基函数(Affinity Propagation Differential evolution-Radial Basis Function，简称APDE-RBF)神经网络的网络安全态势预测方法。

背景技术：

根据2015年1月中国互联网信息中心发布的《第35次中国互联网发展状况报告》显示，截止2014年12月底，我国总体网民中有46.3％的网民遭遇过网络安全问题，表明我国个人互联网使用的安全状况不容乐观。随着网络安全问题日益突出与严重，一些传统的安全防御技术已力不从心，为解决上述问题，网络安全态势感知的研究应运而生。

网络安全态势预测主要是在网络受到攻击损失前网络管理员采取相对应的措施，根据当前和以往的网络安全态势值，建立合理的数学模型对未来一段时间的网络安全状态进行预测。由于网络攻击是随机和不确定的，所以对态势值的预测是一个复杂的非线性过程。

目前研究人员提出了很多预测的方法，如统计方法、灰色预测方法、神经网络方法、马尔科夫模型、支持向量机等，但上述方法都存在各自的局限性与不足。

统计方法较为常用的模型有：自回归模型、滑动平均模型和自回归滑动平均模型，然而这些模型存在以下局限性：时间序列的数据要求平稳,如果是多元回归,还要求变量之间是独立的；灰色预测方法适用单调变化的时间序列，对于波动较大的时间序列难以预测；1987年，Lapdes等人首先将神经网络应用于由计算机产生的时间序列仿真数据的学习和预测，但神经网络存在收敛速度慢、结构选择困难和容易陷入局部极小等问题,同时由于该方法受网络结构复杂度和样本复杂度的影响较大,因而会出现过学习或泛化能力低的现象；马尔科夫模型需要大量复杂的数学公式推导，难以建立准确的预测模型；支持向量机(Support Vector Machine,简称SVM)对大规模训练样本难以实施，收敛速度慢。

技术实现要素：

针对上述现有技术的不足，本发明提出一种基于APDE-RBF神经网络的网络安全态势预测方法，旨在增强泛化能力的同时，提高对网络安全态势的预测精度。

为实现上述目的，本发明提出的一种基于APDE-RBF神经网络的网络安全态势预测方法，其特征在于，该预测方法包括以下步骤：

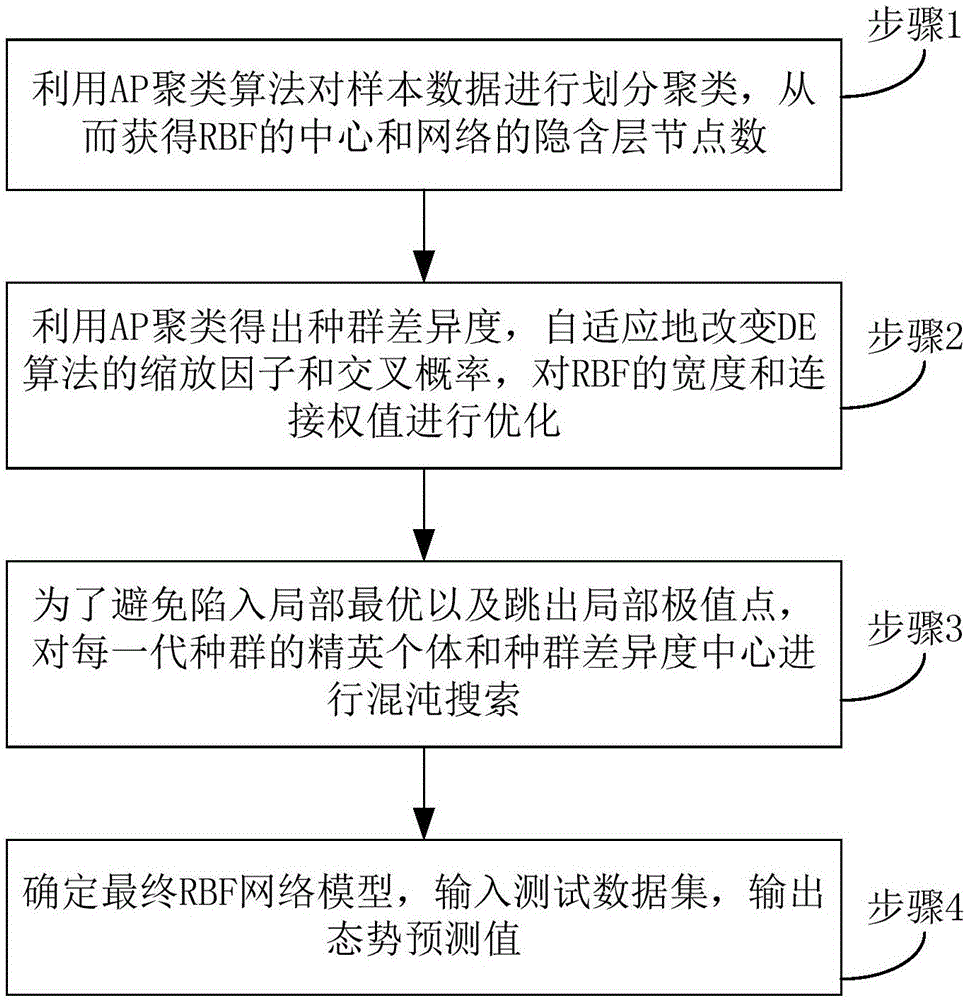
步骤1：利用吸引力传播(Affinity Propagation，简称AP)聚类算法对样本数据进行划分聚类，从而获得RBF的中心和网络的隐含层节点数；

步骤2：利用AP聚类得出种群差异度，自适应地改变差分进化(Differential evolution,简称DE)算法的缩放因子和交叉概率，对RBF的宽度和连接权值进行优化；

步骤3：为了避免陷入局部最优以及跳出局部极值点，对每一代种群的精英个体和种群差异度中心进行混沌搜索；

步骤4：确定最终RBF网络模型，输入测试数据集，输出态势预测值。

优选地，所述步骤1进一步包括以下步骤：

步骤11：利用欧氏距离计算输入节点之间的相似度矩阵S为：S(i,k)＝-||x_i-x_k||²，其中x_i和x_k表示RBF神经网络任意两个输入节点，S(i,k)表示点x_k作为点x_i的聚类中心的相似度；

步骤12：初始化吸引度矩阵R和归属度矩阵A为R(i,k)＝0,A(i,k)＝0，其中R(i,k)表示点x_k适合作为数据点x_i的聚类中心的程度，A(i,k)表示点x_i选择点x_k作为其聚类中心的适合程度；

步骤13：确定偏向参数其中N表示输入节点的数量，median函数表示一组数值中居于中间的数值；

步骤14：根据下述公式计算吸引度矩阵R和归属度矩阵A：

其中p(k)表示数据点x_k作为聚类中心的参考度，R(k,k)表示数据点x_k适合作为自己的聚类中心的程度，A(k,k')表示数据点x_k选择数据点x_k'作为其聚类中心的程度，S(k,k')表示数据点x_k和数据点x_k'的相似程度；从上述公式可看出当p(k)较大时其对应的R(k,k)也会较大，进而A(i,k)取值也会较大，从而类代表k作为最终聚类中心的可能性较大；相应地，当越多的p(k)较大时，越多的类代表倾向于成为最终的聚类中心，因此，增大或者减小p(k)可以增加或减少AP输出的聚类数目；

步骤15：更新吸引度矩阵R和归属度矩阵A的公式为：

R(i,k)＝λ*R(i,k)_old+(1-λ)*R(i,k)_new

A(i,k)＝λ*A(i,k)_old+(1-λ)*A(i,k)_new

上述更新公式表示每次迭代时，新的吸引度矩阵R(i,k)_new和归属度矩阵A(i,k)_new要分别与上一次的R(i,k)_old和A(i,k)_old进行加权更新，得到该次迭代的吸引度矩阵和归属度矩阵，其中λ表示更新因子；

步骤16：如果满足以下条件之一：①选择的类中心保持稳定，②超过最大迭代次数，则转至步骤17，否则转步骤14；

步骤17，输出聚类结果。

优选地，所述步骤2进一步包括以下步骤：

步骤21：执行初始化，过程如下：

σ_i＝σ_min+rand(0,1)*(σ_max-σ_min)

w_i＝rand(0,1)

其中σ_i为RBF神经网络基函数宽度，σ_max表示所有样本数据点中两个最远数据点的距离宽度，其计算公式为：σ_min表示所有样本数据点中两个最近数据点的距离宽度，其计算公式为：w_i表示隐含层到输出层连接权值,rand(0,1)表示(0,1)间均匀分布的随机数；

步骤22：执行变异过程，将第g+1代种群中变异个体V_i(g+1)建模为第g代种群中三个个体的函数：

V_i(g+1)＝X_r1(g)+F*(X_r2(g)-X_r3(g))

i≠r1≠r2≠r3

其中X_i(g)是第g代种群中第i个个体，即X_r1(g)、X_r2(g)和X_r3(g)分别表示第g代种群中第r1个、第r2个以及第r3个个体，F为缩放因子；

步骤23：执行交叉过程，产生第g+1代第i个第j维新个体u_ij(g+1)的公式为：

其中v_ij(g+1)表示第g代种群第i个第j维个体进行变异操作后的个体，x_ij(g)表示第g代种群第i个第j维个体，rand是(0,1)间均匀分布的随机数，j_rand是[1,n]间的随机整数，CR表示交叉概率；上述公式含义为当随机变量rand小于交叉概率CR或者个体中元素对应序数j等于随机变量j_rand，即采用变异个体中的元素作为新个体，旨在提高个体变异的可能性；否则，仍保持目标个体x_ij(g)不变；

步骤24：执行选择过程，如下：

其中U_i(g+1)是候选个体，X_i(g)是对应个体，f(·)是个体的适应度函数，此处使用均方误差(mean square error,简称MSE)作为适应度函数。

进一步，所述步骤22中对缩放因子F进行动态调整的公式为：

其中F_max和F_min分别表示缩放因子的上下界，PD(g)是第g代中的种群差异度，且种群差异度表示对种群空间中所有个体进行聚类所得到的聚类个数，当种群差异度越大时，个体在种群空间中分布越均匀，求得全局最优解可能性越大；τ₁为迭代阈值，g_max为最大迭代次数。

进一步，所述步骤23中的使交叉概率CR可自适应调整的公式为：

其中CR_min和CR_max分别表示交叉概率的上下界，τ₂为设置的迭代阈值。

优选地，所述步骤3中混沌搜索具体实现为：首先建模一维Logistic映射混沌模型，其表达式为：Z^t+1＝μZ^t(1-Z^t)，其中μ是控制参数，是一个随机生成的D维向量，t表示混沌迭代次数；

其次，建模种群中最优个体和差异度中心迭代更新公式：

其中X_i表示种群的最优个体或者差异度中心，表示混沌搜索后的新个体，α表示混沌调节参数，r是[0,1]间的随机数。

本发明的有益效果在于：采用本发明提出的AP聚类算法得出种群差异度，并自适应地改变DE算法的缩放因子和交叉概率，不仅优化了RBF的宽度和连接权值，而且对每一代种群的精英个体和种群差异度中心均进行混沌搜索，避免了陷入局部最优，不但能够增强泛化能力，而且能够提高预测精度。

附图说明

图1是本发明提供的基于APDE-RBF神经网络网络安全态势预测方法的优选实施例流程图；

图2是不同算法态势值预测对比仿真图；

图3是不同算法的不同误差对比仿真图；

图4是不同改进DE算法预测对比仿真图；

图5是不同改进DE算法的不同误差对比仿真图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚明白，下面结合附图对本发明的具体实施方式作进一步详细说明。

图1是本发明提供的基于APDE-RBF神经网络的网络安全态势预测方法的优选实施例流程图，该方法具体包括以下步骤：

步骤1：利用AP聚类算法对样本数据进行划分聚类，从而获得RBF的中心和网络的隐含层节点数；

步骤2：利用AP聚类得出种群差异度，自适应地改变DE算法的缩放因子和交叉概率，对径向基函数RBF的宽度和连接权值进行优化；

步骤3：为了避免陷入局部最优以及跳出局部极值点，对每一代种群的精英个体和种群差异度中心进行混沌搜索；

步骤4：确定最终RBF网络模型，输入测试数据集，输出态势预测值。

根据本发明，所述步骤1中进一步包括以下步骤：

步骤11：利用欧氏距离计算输入节点之间的相似度矩阵S为：S(i,k)＝-||x_i-x_k||²，其中x_i和x_k表示RBF神经网络任意两个输入节点，S(i,k)表示点x_k作为点x_i的聚类中心的相似度；

步骤12：初始化吸引度矩阵R和归属度矩阵A为R(i,k)＝0,A(i,k)＝0，其中R(i,k)表示点x_k适合作为数据点x_i的聚类中心的程度，A(i,k)表示点x_i选择点x_k作为其聚类中心的适合程度；

步骤13：确定偏向参数p_k表示各样本数据点被选作聚类中心的可能性，是相似矩阵S对角线上元素的取值，k＝1,…,N，N表示输入节点的数量，median函数表示一组数值中居于中间的数值；

步骤14：根据下述公式计算吸引度矩阵R和归属度矩阵A：

其中p(k)表示数据点x_k作为聚类中心的参考度，R(k,k)表示数据点x_k适合作为自己的聚类中心的程度，A(k,k')表示数据点x_k选择数据点x_k'作为其聚类中心的程度，S(k,k')表示数据点x_k和数据点x_k'的相似程度；从上述公式可看出当p(k)较大时其对应的R(k,k)也会较大，进而A(i,k)取值也会较大，从而类代表k作为最终聚类中心的可能性较大；相应地，当越多的p(k)较大时，越多的类代表倾向于成为最终的聚类中心，因此，增大或者减小p(k)可以增加或减少AP输出的聚类数目；

步骤15：更新吸引度矩阵R和归属度矩阵A的公式为：

R(i,k)＝λ*R(i,k)_old+(1-λ)*R(i,k)_new

A(i,k)＝λ*A(i,k)_old+(1-λ)*A(i,k)_new

上述更新公式表示每次迭代时，新的吸引度矩阵R(i,k)_new和归属度矩阵A(i,k)_new要分别与上一次的R(i,k)_old和A(i,k)_old进行加权更新，得到该次迭代的吸引度矩阵和归属度矩阵，其中λ表示更新因子；

步骤16：如果满足以下条件之一：①选择的类中心保持稳定，②超过最大迭代次数，则转至步骤17，否则转步骤14；

步骤17，输出聚类结果。

根据本发明，所述步骤2中进一步包括以下步骤：

步骤21：执行初始化，过程如下：

σ_i＝σ_min+rand(0,1)*(σ_max-σ_min)

w_i＝rand(0,1)

其中σ_i为RBF神经网络基函数宽度，σ_max表示所有样本数据点中两个最远数据点的距离宽度，其计算公式为：σ_min表示所有样本数据点中两个最近数据点的距离宽度，其计算公式为：c_i、c_j表示任意两个不同的隐含层节点，w_i表示隐含层到输出层连接权值,rand(0,1)表示(0,1)间均匀分布的随机数；

步骤22：执行变异过程，将第g+1代种群中变异个体V_i(g+1)建模为第g代种群中三个个体的函数：

V_i(g+1)＝X_r1(g)+F*(X_r2(g)-X_r3(g))i≠r1≠r2≠r3

其中X_r1(g)、X_r2(g)和X_r3(g)分别表示第g代种群中第r1个、第r2个以及第r3个个体，F为缩放因子；

步骤23：执行交叉过程，产生新个体u_ij(g+1)的公式如下所示：

其中v_ij(g+1)表示第g代种群第i个第j维个体进行变异操作后的个体，x_ij(g)表示第g代种群第i个第j维个体，rand是(0,1)间均匀分布的随机数，j_rand是[1,n]间的随机整数，CR表示交叉概率；上述公式含义为当随机变量rand小于交叉概率CR或者个体中元素对应序数j等于随机变量j_rand，即采用变异个体中的元素作为新个体，旨在提高个体变异的可能性；否则，仍保持目标个体x_ij(g)不变；

步骤24：执行选择过程，具体如下：

其中U_i(g+1)是候选个体，X_i(g)是对应个体，f(·)是个体的适应度函数，此处使用均方误差(mean square error,简称MSE)作为适应度函数。

根据本发明，所述步骤22中的对F进行动态调整的公式为：

其中F_max和F_min分别表示缩放因子的上下界，PD(g)是第g代中的种群差异度，且种群差异度表示对种群空间中所有个体进行聚类所得到的聚类个数，当种群差异度越大时，个体在种群空间中分布越均匀，求得全局最优解可能性越大；τ₁为设置的迭代阈值，g_max为最大迭代次数。

根据本发明，进一步，所述步骤23中的使交叉概率CR可自适应调整的公式为：

其中CR_min和CR_max是交叉概率的上下界，τ₂是设置的迭代阈值。

根据本发明，进一步，所述步骤3中混沌搜索具体实现为：首先建模一维Logistic映射混沌模型，其表达式为：Z^t+1＝μZ^t(1-Z^t)该式是数学意义上的迭代公式，其值是一个随机生成的D维向量，其中，μ是控制参数，t表示混沌迭代次数；

其次，建模种群中最优个体和差异度中心迭代更新公式：

其中X_i表示种群的最优个体或者差异度中心，表示混沌搜索后的新个体，α表示混沌调节参数，r是[0,1]间的随机数。

为说明本发明的有益效果，根据仿真结果进行进一步分析。

图2描述了基于不同算法得到的网络安全态势值。从图2可以看出，自回归滑动平均模型(Auto-Regressive and Moving Average Model，简称ARMA)主要针对随机平稳的时间序列，但是因为网络攻击的随机性和复杂性，网络安全态势序列是非平稳的；灰色模型(Grey Model，简称GM)对于单调变化的时间序列预测效果好，反之误差大；最小二乘支持向量机(Least Squares Support Vector Machines，简称LSSVM)的支持向量变成了所有数据点，失去了SVM的稀疏性特点；Kmeans-RBF需要预先设定隐含层节点，忽略了数据本身的特点，弱化了RBF的泛化能力，然而，以真实值作为衡量标准，相比于上述方法出现的不同程度的误差和缺陷，本发明提出的APDE-RBF神经网络模型预测精度最高。

图3显示了不同算法的不同误差对比，从图3可以看出不论是平均相对误差、均方根误差还是相对均方误差，APDE-RBF神经网络模型都保持在较小的误差水平，体现了较高的预测精度。

图4显示不同改进DE算法在不同时间点的网络安全态势值。DE算法是固定的F和CR，易陷入局部最优；简化的差分进化版本(Simplified Differential Evolution Version，简称SDE)算法的F采用简单的随机数；基于全体参数和变异策略的差分进化算法(Differential evolution algorithm with ensemble of parameters and mutation strategies，简称EPSDE)算法利用变异策略池和参数池随机组合进行迭代进化；自适应差分进化(Self-Adaptive Differential Evolution，简称jDE)算法的F和CR依赖随机数判别从而得到不同的结果；基于复合试验向量生成策略和控制参数的差分进化(Evolution With Composite Trial Vector Generation Strategies and Control Parameters，简称CoDE)算法是利用三种不同的变异策略和参数设置竞争耦合进行迭代进化。上述方法虽然对DE算法的变异策略和参数设置进行自适应改进，但是大多都是随机数或依赖随机数进行判别选取，导致进化不稳定。进一步，从图中可以看出，以真实值作为衡量标准，相比于上述算法，APDE算法总体上维持了较低的绝对误差，其原因在于APDE-RBF神经网络模型依赖种群差异度和迭代进化程度对F和CR进行自适应调整，使种群向有利方向进化，加快了算法的收敛速度。

图5是不同算法的不同误差对比，从图5可以看出不论是平均相对误差、均方根误差还是相对均方误差，本发明提出的APDE-RBF神经网络模型都保持在较小的误差水平，体现了较高的预测精度。

本发明所举实施方式或者实施例对本发明的目的、技术方案和优点进行了进一步的详细说明，所应理解的是，以上所举实施方式或者实施例仅为本发明的优选实施方式而已，并不用以限制本发明，凡在本发明的精神和原则之内对本发明所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。