一种微分对策反拦截机动突防/精确打击导引方法与流程

本发明提供了一种微分对策反拦截机动突防/精确打击导引方法，它涉及微分对策反拦截机动突防和落点精度控制，属于航天技术、武器
技术领域：

背景技术：
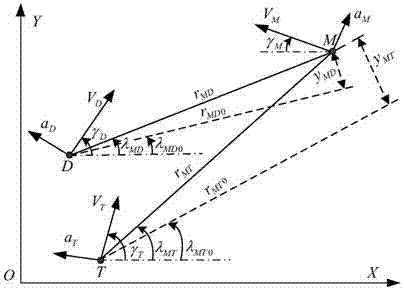
：随着现代制导律以及反导系统的发展，导弹的生存环境恶化，机动突防是提高导弹生存概率的重要手段，因此很有必要进行深入研究。现今，研究较多的导弹的机动突防方式主要有两类：程序式机动和最优机动(最优机动是假设拦截弹采用比例导引律(后面直接用PN表示比例导引律)条件下，以脱靶量最大为目的，基于最优控制理论得到的最优机动方式，后续涉及“最优机动”时，定义与此处相同，不再说明)。程序式机动工程实现性强且对落点精度的影响小，但是突防概率低；最优机动突防概率高，但是容易引起大的落点偏差。微分对策理论研究的是双边或者多边同时达到性能指标最优的问题，本发明基于微分对策理论，在研究导弹反拦截机动突防的同时，对导弹的落点精度进行控制，使得本发明在保持高突防概率的条件下，还能够精确地打击目标。技术实现要素：本发明的目的是提供一种微分对策反拦截机动突防/精确打击导引方法，通俗地讲，是找到一种最优的控制律，使得导弹能够以最大的脱靶量突防防御弹，实现反拦截机动突防，同时能够以最小的落点偏差命中目标，实现精确打击。因而，既需要关注导弹和防御弹之间的交战、又需要关注导弹和目标之间的交战。本发明将攻防对抗研究的主体由传统的两个参与方(即目标、导弹)扩展到三个参与方(即目标弹、导弹、防御弹)。首先根据交战三方的相对运动学关系及各自的动力学环节建立了三体微分对策模型。该模型的指标函数既包含了导弹突防防御弹的脱靶量，又包含了导弹攻击目标的落点精度。如此，就可以将本发明所关心的突防脱靶量和落点精度放到一个模型中进行研究。其次，为了简化微分对策问题求解难度，引入新的状态量，对原三体微分对策模型进行降维处理，得到新的三体微分对策模型。最后，基于最优控制理论对新的三体微分对策模型进行求解，即可得到本发明的解析表达式。本发明一种微分对策反拦截机动突防/精确打击导引方法，它包括以下三个步骤：步骤一：三体微分对策模型建模；包括交战三方的动力学环节模型、交战三方线性化交战模型、三体微分对策模型；1.交战三方的动力学环节模型对导弹制导系统来说，动力学环节反映的是导弹实际加速度与指令加速度的关系，指令加速度是导弹的理论控制量，实际加速度是导弹实际能够产生的控制量；本发明假设交战三方的动力学环节均可以用一阶惯性环节代替，根据自动控制原理中一阶惯性环节输入输出量的关系，可得交战三方各自的指令加速度和实际加速度的关系，也即交战三方的动力学环节模型，具体如下：式中，字母M、T、D分别表示导弹、目标和防御弹；uM、uT、uD分别为导弹、目标及防御弹的指令加速度大小，它们是理论控制量；aM、aT、aD分别为导弹、目标及防御弹的实际加速度大小，它们是实际控制量；分别为aM、aT、aD对时间的导数；τM、τT、τD分别为导弹、目标及防御弹的一阶惯性环节的时间常数；2.交战三方线性化交战模型研究的是导弹的末制导律，在末段，相对速度较大，交战时间很短，假设交战三方的加速度方向垂直于各自的速度方向，即加速度只改变速度的方向而不改变速度的大小，这一假设比较符合实际，在末制导律的设计中很常用；交战参与方有导弹、目标及防御弹三个，涉及到两个初始碰撞三角形，分别是导弹-目标初始碰撞三角形、导弹-防御弹初始碰撞三角形，在末段，交战时间很短，相对速度很大，且认为中制导能够为末制导提供较好的制导条件，故假设交战参与方的弹道可以沿着对应的初始碰撞三角形进行线性化。线性化假设在末制导律的设计中非常普遍，也具有很高的精度；(1)根据加速度垂直于速度方向这一假设，对于导弹和目标这一对交战方，可以写出，二者在垂直于目标视线方向上的相对加速度，具体如下：假设导弹和目标的弹道可以沿着导弹-目标初始碰撞三角形进行线性化，即二者的弹道与初始碰撞三角形对应边的偏差量很小，转化成数学语言就是如下表达式：γT≈γT0、γM≈γM0、λMT≈λMT0从而，二者在垂直于目标视线方向上的相对加速度可以简化为如下形式：上述三个式子中，字母M、T分别表示导弹和目标；aM、aT分别为导弹和目标的实际加速度大小；γM、γT分别为导弹和目标的弹道倾角，γM0、γT0是对应的初值；λMT是导弹-目标交战主体对应的目标视线角，λMT0是对应的初值；是导弹和目标在垂直于二者初始视线方向上的相对加速度，积分两次即可得到yMT，对于线性化交战模型，yMT在拦截时刻的值即为导弹拦截目标的脱靶量；(2)根据加速度垂直于速度方向这一假设，对于导弹和防御弹这一对交战方，可以写出，二者在垂直于目标视线方向上的相对加速度，具体如下：假设导弹和防御弹的弹道可以沿着导弹-防御弹初始碰撞三角形进行线性化，即二者的弹道与初始碰撞三角形对应边的偏差量很小，转化成数学语言就是如下表达式：γD≈γD0、γM≈γM0、λMD≈λMD0从而，二者在垂直于目标视线方向上的相对加速度可以简化为如下形式：上述三个式子中，字母M、D分别表示导弹和防御弹；aM、aD分别为导弹和防御弹的实际加速度大小；γM、γD分别为导弹和防御弹的弹道倾角，γM0、γD0是对应的初值；λMD是导弹-防御弹交战主体对应的目标视线角，λMD0是对应的初值；是导弹和防御弹在垂直于二者初始视线方向上的相对加速度，积分两次即可得到yMD，对于线性化交战模型，yMD在拦截时刻的值即为防御弹拦截导弹的脱靶量；为使微分方程形式简洁，便于书写，将上列(1)和(2)中相对加速度表达式写成如下形式：式中，θT0、θM0、θD0、θ0的表达式如下：θT0＝γT0-λMT0θM0＝γM0+λMT0θD0＝γD0-λMD0θ0＝λMT0-λMD0式中，γT0、γM0、γD0、λMT0、λMD0的定义同本步骤序号2。上述微分方程组即是线性化交战相对运动学模型。3.三体微分对策模型(1)三体微分对策模型的系统方程将上面序号1处的动力学环节模型和序号2处的线性化交战相对运动学模型写成一个微分方程组，如下：本发明的目的是找到一个最优的控制律，使得导弹能够以最大的脱靶量突防防御弹，同时能够以最小的落点偏差命中目标，因而，既需要关注防御弹和导弹之间的脱靶量、又需要关注导弹和目标之间的脱靶量。在序号2线性化交战模型处已经交代过，对于线性化交战模型，导弹和目标之间的脱靶量(或者说导弹攻击目标的落点偏差)就是yMT在对应拦截时刻的值，防御弹和导弹之间的脱靶量就是yMD在对应拦截时刻的值。因此，yMT、yMD须包含在三体微分对策模型的状态变量中，结合上述微分方程组，三体微分对策模型的状态变量可以归纳如下：式中，X表示状态变量矢量，它是个7维的列向量，上标T表示向量转置，xi,i＝1…7表示第i个状态变量；表示yMT对时间的一阶导数，反映的是导弹和目标在垂直初始目标视线方向上的相对速度；表示yMD对时间的一阶导数，反映的是导弹和防御弹在垂直初始目标视线方向上的相对速度；aM、aT、aD、τM、τT、τD的定义同序号1；假设导弹和防御弹的交战完成时刻要早于导弹和目标交战完成时刻，则防御弹和导弹交战完成后，防御弹消失，剩下导弹和目标，交战的主体由原来的三个变成了两个，为了保持三体微分对策模型的一致性，引入阶跃函数δ，阶跃函数的定义如下：式中，t是当前时刻，tf2是防御弹和导弹交战的完成时刻；分别将上述7个状态变量对时间求一阶导数，并结合上述微分方程组，可以得到如下由七个微分方程组成的微分方程组：将上述微分方程组写成状态空间形式，具体如下：式中，上标T表示向量转置；A、B和C均为常系数矩阵，表达式如下：C＝[0000001/τM]T上述状态空间表达式即为三体微分对策模型的系统方程；(2)三体微分对策模型的指标函数序号(1)给出了三体微分对策模型的系统方程，对于一个完整微分对策模型，还需要补充指标函数；导弹一方面要以较大的脱靶量突防防御弹，保证自身的生存概率，另一方面要以较小的落点偏差命中目标，保证命中精度；对于导弹来说，期望突防防御弹的脱靶量最大，且攻击目标的落点偏差最小，同时自身消耗的能量最小；对于防御弹和目标这一对组合来说，期望防御弹拦截导弹的脱靶量最小，且目标规避导弹攻击的落点偏差最大，同时消耗的能量最小；在序号2线性化交战模型处已经交代过，对于线性化交战模型，导弹和目标之间的脱靶量可以用yMT在对应拦截时刻的值表示，防御弹和导弹之间的脱靶量也可以用yMD在对应拦截时刻的值表示，各自的能量消耗可以通过控制量平方对时间的积分来表示，因此，三体微分对策模型的指标函数可以用下式表示：对于导弹来说，期望找到最优控制律使得指标函数J最大，即maxJ，对于目标和防御弹这对组合来说，期望找到最优控制律使得指标函数J最小，即minJ，这是一个典型的双边最优控制问题，后续需要应用最优控制理论进行求解。上式中，J是三体微分对策模型的指标函数；tf1、tf2分别是导弹和目标之间、导弹和防御弹之间交战的拦截时刻(即完成时刻)；yMT(tf1)是在拦截时刻tf1，导弹和目标在垂直于二者初始视线方向上的偏差量，即为导弹和目标之间的落点偏差；yMD(tf2)是在拦截时刻tf2，导弹和防御弹在垂直于二者初始视线方向上的偏差量，即导弹和目标之间的脱靶量；aMT、aMD分别是与yMT(tf1)、yMD(tf2)相关的权重系数，均为非负数；uM、uT、uD分别为导弹、目标及防御弹的指令加速度大小，或者说控制量；βT、βD分别是与积分相关的权重系数，均为非负数；t是时间，右侧积分项表示对时间t的积分；tf1、tf2的表达式如下所示：tf1＝RMT0/(VMcosθM0+VTcosθT0)tf2＝RMD0/(VMcosθM0+VDcosθD0)式中，VM、VT、VD分别为导弹、目标及防御弹的速度大小；RMT0、RMD0分别为导弹和目标、导弹和防御弹之间的初始距离；θM0、θT0、θD0的定义同序号2；如此，就建立了三体微分对策模型；序号1和2提供了三体微分对策模型的原始微分方程组，序号3的(1)对原始微分方程组进行处理，得到三体微分对策模型的系统方程，结合(2)的指标函数，组成了三体微分对策模型；步骤二：对原三体微分对策模型进行降维处理得到新的三体微分对策模型；包括零控脱靶量矢量的定义、新三体微分对策模型的系统方程、新三体微分对策模型指标函数；1.零控脱靶量矢量的定义原三体微分对策模型的系统方程包含七个微分方程，是七维的，后续求解需要进行多次积分，处理起来较为复杂。为了简化求解难度，定义新的状态量，即零控脱靶量矢量ZEM，将原七维问题降阶为二维问题，ZEM的定义式如下：式中，z1、z2是ZEM的两个分量，z1是从当前时刻t到拦截时刻tf1，导弹和目标都不施加控制时得到的脱靶量，即零控脱靶量；z2是从当前时刻t到拦截时刻tf2，防御弹和导弹都不施加控制时得到的脱靶量；X是原三体微分模型的七维状态变量矢量；D是常系数矩阵；Φ(tf-t)是原三体微分对策模型的，从t时刻到tf时刻的状态转移矩阵，关于状态转移矩阵的概念可以参考现代控制理论相关书目；tf1、tf2分别是导弹和目标之间的拦截时刻、导弹和防御弹之间的拦截时刻；D矩阵为：状态转移矩阵可以通过下式进行求解：Φ(tf-t)＝L-1[(sI-A)-1]式中，I是7阶单位矩阵；A是原三体微分对策模型系统方程中的常系数矩阵(参考步骤一)；s是频域变量；(sI-A)-1表示对矩阵(sI-A)求逆；L-1(·)表示拉普拉斯逆变换；代入A的表达式，可以得到状态转移矩阵的表达式为：将状态转移矩阵Φ(tf1-t)、Φ(tf2-t)，系数矩阵D以及原三体微分对策模型的状态变量矢量X代入ZEM的定义式中，可以得到ZEM的表达式如下式中，tgo1是导弹和目标之间的剩余飞行时间，它等于拦截时刻tf1与当前时刻t之差；tgo2是导弹和防御弹之间的剩余飞行时间，它等于拦截时刻tf2与当前时刻t之差；tf1、tf2、aT、aM、aD、τT、τM、τD、yMT、yMD、θ0定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)的表达式为：fT(t)＝cosθT0τTψ(εT1)fD(t)＝cosθD0τDψ(εD2)fM1(t)＝cosθM0τMψ(εM1)fM2(t)＝cosθM0τMψ(εM2)式中，θT0、θD0、θM0的定义同步骤一；εT1、εD2、εM1、εM2及ψ(ε)函数的表达式如下：εT1＝tgo1/τTεD2＝tgo2/τDεM1＝tgo1/τMεM2＝tgo2/τMψ(ε)＝e-ε+ε-1式中，tgo1、tgo2的定义同上；ε是任意变量；e是自然底数；2.新三体微分对策模型的系统方程本步骤中，序号1定义了零控脱靶量矢量ZEM，它包含两个分量z1、z2，二者的表达式同序号1。将z1、z2的表达式对时间t求一阶导数，并结合步骤一处的系统方程，得到如下两个微分方程：式中，分别表示z1、z2对时间t的一阶导数；uM、uT、uD、θ0、δ的定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)的定义同本步骤的序号1。这两个微分方程等价替换了原三体微分对策模型的系统方程，构成了新三体微分对策模型的系统方程。可以看出，原三体微分对策模型的系统方程包含7个微分方程，本步骤通过定义新的状态变量矢量ZEM后,只需要用2个微分方程就可等价替换原7个微分方程，大大简化了后续求解难度。3.新三体微分对策模型指标函数根据零控脱靶量的物理意义，在拦截时刻，零控脱靶量就是实际交战的脱靶量，因此有下述式子成立：yMT(tf1)＝z1(tf1)yMD(tf2)＝z2(tf2)从而，原三体微分对策模型的指标函数就可以等价替换为如下形式：式中，J′是与原指标函数等价的新指标函数，它是新三体微分对策模型的指标函数；z1(tf1)是z1在拦截时刻tf1对应的值，它和步骤一中指标函数处的脱靶量yMT(tf1)是等价的；z2(tf2)是z2在拦截时刻tf2对应的值，它和步骤一中指标函数处的脱靶量yMD(tf2)是等价的；uM、uT、uD、aMT、aMD、βT、βD、tf1、tf2定义同步骤一。对于导弹来说，期望使指标函数最大，即maxJ′，对于目标和防御弹这对组合来说，期望使指标函数最小，即minJ′，这是一个典型的双边最优控制问题，需要用最优控制理论进行求解，求解过程在步骤三给出。本步骤中，序号2处的新三体微分对策模型的系统方程，和序号3处新三体微分对策模型的指标函数，共同组成了新三体微分对策模型。新模型是二维的，相比于原模型，形式上更简洁，后续求解也更加简单。步骤三：基于最优控制理论求解新三体微分对策模型，得到导弹的最优控制律；包括新三体微分对策模型的哈密顿函数、新三体微分对策模型对应的最优控制问题的求解；1.新三体微分对策模型的哈密顿函数新三体微分对策模型实际上是一个双边最优控制问题，要求解该最优控制问题，首先需要建立模型所对应的哈密顿函数。根据最优控制理论相关知识，新三体微分对策模型所对应的哈密顿函数为：将表达式(步骤二的序号2)带入上式，即可得到本模型对应的哈密顿函数，具体如下：式中，H是新三体微分对策模型所对应的哈密顿函数；λ1、λ2分别是与相关的协态变量；的定义同步骤二；uM、uT、uD、βT、βD的定义同步骤一。2.基于最优控制理论求解新三体微分对策模型所对应的最优控制问题新三体微分对策模型实际上是双边最优控制问题，一方(导弹)期望指标函数最大，另一方(目标和防御弹组合)期望指标函数最小，这是一个典型的最优控制问题，对该问题，最优控制理论给出了具体的求解方法。下面基于最优控制理论，求解新三体微分对策模型对应的最优控制问题，具体如下：在最优控制理论中，协态方程反映的是哈密顿函数对状态量的偏导数与协态变量一阶导数的关系，具体为式中，X是任意最优控制问题的状态变量矢量。对于新三体微分对策模型，状态变量矢量是ZEM，它包含z1、z2两个状态量，可得本问题的协态方程为：式中分别是协态变量λ1、λx对时间的导数；分别表示哈密顿函数H对状态量z1、z2的偏导数，z1、z2的定义同步骤二；由于本问题的哈密顿函数H不显含状态量z1、z2，故：从而有：在最优控制理论中，通常将指标函数中与终端状态相关项记为是终端时刻tf和终端状态X(tf)的函数。横截条件反映的是协态变量的终端值与函数与对应状态量偏导数的关系，具体为：式中，X是任意最优控制问题的状态变量矢量，λ是对应的协态变量矢量，tf是对应的终端时刻。针对本问题，首先根据指标函数(步骤二的序号3处)：可以写出函数再根据函数，可以写出本问题的横街条件，如下：式中，表示函数对状态量z1、z2的偏导数。代入的表达式，得到λ1、λ2在拦截时刻的值，如下：λ1(tf1)＝-αMTz1(tf1)，λ2(tf2)＝αMDz2(tf2)式中，λ1(tf1)是协态变量λ1在拦截时刻tf1对应的值；λ2(tf2)是协态变量λ2在终端时刻值tf2对应的值；tf1、tf2的定义同步骤一；z1(tf1)、z2(tf2)的定义同步骤二；aMT、aMD的定义同步骤一；根据协态方程结果和λ1(tf1)、λ2(tf2)的表达式，可得到协态变量λ1、λ2的表达式为：λ1＝-αMTz1(tf1)，λ2＝αMDz2(tf2)式中，z1(tf1)、z2(tf2)的定义同步骤二；aMT、aMD的定义同步骤一；在最优控制理论中，耦合方程反映的是哈密顿函数与控制量的关系，当控制量使得哈密顿函数取得极值时，即为最优控制律，耦合方程表达式为：式中，u是任意最优控制问题的控制量矢量。对于本问题，控制量矢量u＝[uT；uD；uM]，即本问题的耦合方程为：式中，分别表示哈密顿函数H对控制量uM、uT、uD的偏导数；uM、uT、uD的定义同步骤一；将本步骤序号1处哈密顿函数H的表达式代入上述耦合方程，即可得到如下方程组：代入上面求得的λ1、λ2表达式，就可以得到交战三方的最优控制律，表达式如下：式中，分别是导弹、目标、防御弹的最优控制律；aMT、aMD、βT、βD、θ0、δ的定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)、z1(tf1)、z2(tf2)的定义同步骤二；三者的最优控制律均是z1(tf1)、z2(tf2)的显示表达式，然而，在实际交战中，并不知道终端时刻的零控脱靶量z1(tf1)、z2(tf2)，只能够通过当前交战双方的信息计算当前时刻的零控脱靶量z1(t)、z2(t)，因此，很有必要建立z1(t)、z2(t)和z1(tf1)、z2(tf2)的显示关系。将最优控制律代入新三体微分对策模型的系统方程中(步骤二的序号2)：得到将得到的微分方程在[t，tf1]内对时间积分，且考虑到阶跃函数δ的表达式(步骤一)：以及，导弹和防御弹的交战完成时刻要先于导弹和目标的交战完成时刻，即tf2＜tf1。得到关于z1(tf1)、z2(tf2)的线性方程组，如下：式中，t是当前时刻，z1(t)是当前时刻，导弹和目标之间的零控脱靶量，z2(t)是当前时刻，导弹和防御弹之间的零控脱靶量，后面为了书写方便，分别记为z1、z2(后面不再说明)。系数矩阵K的表达式如下：式中，gMT、gMD、kMT、kMD的表达式为：gMT＝αMT[h(εT1)/βT-h(εM1)]gMD＝αMDcosθ0h′(εM2)kMT＝αMTcosθ0h′(εM2)kMD＝αMD[h(εD2)/βD-cos2θ0h(εM2)]式中，aMT、aMD、βT、βD、θ0定义同步骤一；εT1、εD2、εM1、εM2的定义同步骤二；h(εT1)、h(εM1)、h(εD2)、h(εM2)、h′(εM2)的表达式如下：式中，εT1、εD2、εM1、εM2、函数ψ(ε)的表达式同步骤二；θT0、θD0、θM0、τT、τD、τM的定义同步骤一；函数k1(ε)、k2(ε)、k3(ε)、g(ε)、ΔεM表达式如下：k1(ε)＝(-0.5e-2ε-2εe-ε+ε3/3-ε2+ε+0.5)k2(ε)＝-(ε+1)e-ε+ε3/3-0.5ε2+1k3(ε)＝-e-ε+0.5ε2-ε+1g(ε)＝e-εΔεM＝(tf1-tf2)/τM式中ε为任意变量；e为自然底数；tf1、tf2的定义同步骤一；根据克莱姆法则，求解上述线性方程组，得到z1(tf1)、z2(tf2)的表达式如下：式中，Δ是系数矩阵K的行列式；Δ11、Δ12、Δ21、Δ22分别是行列式Δ对应下标元素的代数余子式，如Δ12表示行列式Δ对应第1行第2列元素的代数余子式；上述表达式建立了终端时刻零控脱靶量z1(tf1)、z2(tf2)和当前时刻零控脱靶量z1、z2的显示关系。将z1(tf1)、z2(tf2)的表达式代入导弹的最优控制律中，并进行整理，即得到导弹的最优控制律即是一种微分对策反拦截机动突防/精确打击导引方法；式中，第一项用于导引导弹拦截目标，即落点精度控制作用，第二项用于导引导弹规避防御弹的拦截，即起突防作用。tgo1、tgo2、z1、z2的定义同步骤二；NM1是关于零控脱靶量z1的有效导航系数；NM2是关于零控脱靶量z2的有效导航系数，NM1、NM2的表达式为：式中，aMT、aMD、tgo1、tgo2、θ0的定义同步骤一；tgo1、tgo2、fM1(t)、fM2(t)的定义同步骤二；Δ11、Δ12、Δ21、Δ22、Δ的定义同步骤三；上述三个步骤中，步骤一是根据交战三方的动力学环节和线性化相对运动学模型建立三体对抗微分对策模型；考虑到步骤一的三体微分对策模型是七维的，求解难度较大，步骤二对其进行了处理，通过零控脱靶量矢量将原七维问题降阶成二维问题，得到了新的三体微分对策模型；步骤三是基于最优控制理论，对新三体微分对策模型所对应的双边最优控制问题进行求解，得到导弹的最优控制律，该最优控制律即是一种微分对策反拦截机动突防/精确打击导引方法。通过上述三个步骤，描述了三体微分对策模型的建立过程、新旧模型的转换过程以及微分对策模型的求解过程。最终得到了一种微分对策反拦截机动突防/精确打击导引方法。本发明的优点在于：(1)本发明是一种微分对策反拦截机动突防/精确打击导引方法，它同时考虑了导弹的突防和落点精度控制，使得导弹在突防过程能够兼顾落点精度控制，它的表达式包含了两项，与z2相关项用于导引导弹规避防御弹的拦截，即起突防作用，与z1相关项用于导引导弹拦截目标，即起控制落点精度作用。(2)本发明同传统的程序式机动相比，其突防脱靶量大；同最优机动相比，其落点精度高，故而本发明的综合性能优异。(3)本发明具有十分简洁的表达式，表达式中的各项的物理意义清晰明确。附图说明图1是本发明所述方法的流程图。图2是三体对抗几何关系图。图3是方案一，即导弹不进行机动突防，直接采用PN攻击目标方案，交战三方的弹道曲线。图4是方案二，即导弹先采用蛇形机动进行机动突防，再采用PN攻击目标方案，交战三方的弹道曲线。图5是方案三，即导弹先采用最优机动进行机动突防，再采用PN攻击目标方案，交战三方的弹道曲线。图6是方案四，即导弹采用本发明进行机动突防和攻击目标方案，交战三方的弹道曲线。图7是不同机动能力条件下，导弹采用本发明进行机动突防和攻击目标时，对应的弹道曲线族。图8是不同机动能力条件下，导弹采用本发明进行机动突防和攻击目标时，突防脱靶量和落点偏差曲线。上述图中，涉及到的符号、代号说明如下：图2～图8中字母M、T、D分别表示导弹、目标及防御弹。图2中，OXY表示惯性坐标系；VM、VT、VD、γM、γT、γD分别为导弹、目标及防御弹的速度、导弹倾角；rMT、λMT分别导弹和目标之间的距离、视线角，rMT0、λMT0是对应的初值；rMD、λMD分别导弹和防御弹之间的距离、视线角，rMD0、λMD0是对应的初值；yMD是导弹和防御弹在垂直于二者初始视线方向上的偏差量；yMT是弹道和目标在垂直于二者初始目标视线方向上的偏差量。图3～7中，横坐标X表示惯性坐标系的X轴，单位为米，符号m；纵坐标Y表示惯性坐标系的Y轴，单位为米，符号m。图7～8中，aDmax表示防御弹的最大机动能力，aTmax表示目标的最大机动能力，aMmax表示导弹的最大机动能力，g表示重力加速度常量，取为9.8m/s2，单位中m表示米，s表示秒。具体实施方式下面将结合附图和实施案例对本发明作进一步的详细说明。本发明一种微分对策反拦截机动突防/精确打击导引方法，它包括三个步骤，具体流程如图1所示，下面我们具体介绍上述三个步骤。步骤一：三体微分对策模型建模。包括交战三方的动力学环节模型、交战三方线性化交战模型、三体微分对策模型；1.交战三方的动力学环节模型对导弹制导系统来说，动力学环节反映的是导弹实际加速度与指令加速度的关系。本发明假设交战三方的动力学环节均可以用一阶惯性环节代替，根据自动控制原理中一阶惯性环节输入输出量的关系，可得交战三方指令加速度和实际加速度的关系，也即交战三方的动力学环节模型，具体如下：式中，字母M、T、D分别表示导弹、目标和防御弹；uM、uT、uD分别为导弹、目标及防御弹的指令加速度大小；aM、aT、aD分别为导弹、目标及防御弹的实际加速度大小；分别为aM、aT、aD对时间的导数；τM、τT、τD分别为导弹、目标及防御弹的一阶延迟环节的时间常数。2.交战三方线性化交战模型研究的是导弹的末制导律，在末段，相对速度较大，交战时间很短，假设交战三方的加速度方向垂直于各自的速度方向，即加速度只改变速度的方向而不改变速度的大小，这一假设比较符合实际，在末制导律的设计中很常用。交战参与方有导弹、目标及防御弹三个，涉及到两个初始碰撞三角形，分别是导弹-目标初始碰撞三角形、导弹-防御弹初始碰撞三角形。(1)根据加速度垂直于速度方向这一假设，对于导弹和目标这一对交战方，可以写出二者在垂直于目标视线方向上的相对加速度，具体如下：假设导弹和目标的弹道可以沿着导弹-目标初始碰撞三角形进行线性化，即二者的弹道与初始碰撞三角形对应边的偏差量很小，转化为数学语言就是有如下表达式成立：γT≈γT0、γM≈γM0、λMT≈λMT0(3)从而，二者在垂直于目标视线方向上的相对加速度可以简化为如下形式：上述三个式子中，字母M、T分别表示导弹和目标；aM、aT分别为导弹和目标的实际加速度大小；γM、γT分别为导弹和目标的弹道倾角，γM0、γT0是对应的初值；λMT是导弹-目标交战主体对应的目标视线角，λMT0是对应的初值；是导弹和目标在垂直于二者初始视线方向上的相对加速度，积分两次即可得到yMT，对于线性化交战模型，yMT在拦截时刻的值即为导弹拦截目标的脱靶量；(2)根据加速度垂直于速度方向这一假设，对于导弹和防御弹这一对交战方，可以写出，二者在垂直于目标视线方向上的相对加速度，具体如下：假设导弹和防御弹的弹道可以沿着导弹-防御弹初始碰撞三角形进行线性化，即二者的弹道与初始碰撞三角形对应边的偏差量很小，转化为数学语言就是有如下表达式成立：γD≈γD0、γM≈γM0、λMD≈λMD0(6)从而，二者在垂直于目标视线方向上的相对加速度可以简化为如下形式：上述三个式子中，字母M、D分别表示导弹和防御弹；aM、aD分别为导弹和防御弹的实际加速度大小；γM、γD分别为导弹和防御弹的弹道倾角，γM0、γD0是对应的初值；λMD是导弹-防御弹交战主体对应的目标视线角，λMD0是对应的初值；是导弹和防御弹在垂直于二者初始视线方向上的相对加速度，积分两次即可得到yMD，对于线性化交战模型，yMD在拦截时刻的值即为防御弹拦截导弹的脱靶量；为使得微分方程形式简洁，便于书写，将上列(1)和(2)中相对加速度表达式(4)和(7)写成如下形式：式中，θT0、θM0、θD0、θ0的表达式如下：式中，γT0、γM0、γD0、λMT0、λMD0的定义同序号2；3.三体微分对策模型(1)三体微分对策模型的系统方程将序号1处的动力学环节模型(1)和序号2处线性化交战相对运动学模型(8)写成一个微分方程组，如下：本发明的目的是找到一个最优的控制律，使得导弹能够以最大的脱靶量突防防御弹，同时能够以最小的落点偏差命中目标，因而，既需要关注防御弹和导弹之间的脱靶量、又需要关注导弹和目标之间的脱靶量。在序号2线性化交战模型处已经交代过，对于线性化交战模型，导弹和目标之间的脱靶量(或者说导弹攻击目标的落点偏差)就是yMT在对应拦截时刻的值，防御弹和导弹之间的脱靶量就是yMD在对应拦截时刻的值。因此，yMT、yMD须包含在三体微分对策模型的状态变量中，结合上述微分方程组，三体微分对策模型的状态变量可以归纳如下：式中，X表示状态变量矢量，它是个7维的列向量，上标T表示向量转置，xi,i＝1…7表示第i个状态变量；表示yMT对时间的一阶导数，反映的是导弹和目标在垂直初始目标视线方向上的相对速度；表示yMD对时间的一阶导数，反映的是导弹和防御弹在垂直初始目标视线方向上的相对速度。假设导弹和防御弹的交战完成时刻要早于导弹和目标交战完成时刻，则防御弹和导弹交战完成后，防御弹消失，剩下导弹和目标，交战的主体由原来的三个变成了两个，为了保持三体微分对策模型的一致性，引入阶跃函数δ，阶跃函数的定义如下：式中，t是当前时刻，tf2是防御弹和导弹交战的完成时刻。将上述7个状态变量对时间求一阶导数，并结合微分方程组(10)，可以得到如下由7个微分方程组成的微分方程组：将上述微分方程组(13)写成状态空间形式，具体如下：式中，上标T表示向量转置，uM、uT、uD分别为导弹、目标及防御弹的指令加速度；A、B和C均为常系数矩阵，表达式如下：C＝[0000001/τM]T式中，θT0、θM0、θD0、θ0、τT、τM、τD、δ的定义同本步骤。上述状态空间表达式(14)即为三体微分对策模型的系统方程。(2)三体微分对策模型的指标函数序号(1)给出了三体微分对策模型的系统方程，对于一个完整微分对策模型，还需要补充指标函数。导弹一方面要以较大的脱靶量突防防御弹，保证自身的生存概率，另一方面要以较小的落点偏差命中目标，保证命中精度。对于导弹来说，期望突防防御弹的脱靶量最大，且攻击目标的落点偏差最小，同时自身消耗的能量最小。对于防御弹和目标这一对组合来说，期望防御弹拦截导弹的脱靶量最小，且目标规避导弹攻击的落点偏差最大，同时消耗的能量最小。在序号2处已经交代过，对于线性化交战模型，导弹和目标之间的脱靶量(或者说导弹攻击目标的落点偏差)就是yMT在对应拦截时刻的值，防御弹和导弹之间的脱靶量就是yMD在对应拦截时刻的值，各自的能量消耗可以通过控制量平方对时间的积分来表示，因此，三体微分对策模型的指标函数可以用下式表示：对于导弹来说，期望找到最优控制律使得指标函数J最大，即maxJ，对于目标和防御弹这对组合来说，期望找到最优控制律使得指标函数J最小，即minJ，这是一个典型的双边最优控制问题，后续需要应用最优控制理论进行求解。上式中，J是三体微分对策模型的指标函数；tf1、tf2分别导弹和目标之间、导弹和防御弹之间交战的完成时刻(或者称拦截时刻)；yMT(tf1)是在拦截时刻tf1，导弹和目标在垂直于二者初始视线方向上的偏差量，即为导弹和目标之间的落点偏差；yMD(tf2)是在拦截时刻tf2，导弹和防御弹在垂直于二者初始视线方向上的偏差量，即导弹和目标之间的脱靶量；aMT、aMD分别是与yMT(tf1)、yMD(tf2)相关的权重系数，均为非负数；uM、uT、uD分别为导弹、目标及防御弹的指令加速度大小，或者说控制量；βT、βD分别是与积分相关的权重系数，均为非负数；t是时间，右侧积分项表示对时间t的积分；tf1、tf2的表达式如下所示：tf1＝RMT0/(VMcosθM0+VTcosθT0)(17)tf2＝RMD0/(VMcosθM0+VDcosθD0)(18)式中，VM、VT、VD分别为导弹、目标及防御弹的速度大小；RMT0、RMD0分别为导弹和目标、导弹和防御弹之间的初始距离；θM0、θT0、θD0的定义同序号2；如此，就建立了三体微分对策模型。本步骤中，序号1和2提供了三体微分对策模型的原始微分方程组，序号3的(1)对原始微分方程组进行处理，得到三体微分对策模型的系统方程，结合(2)的指标函数，组成了三体微分对策模型。步骤二：对原三体微分对策模型进行降维处理得到新三体微分对策模型。包括零控脱靶量矢量的定义、新三体微分对策模型的系统方程、新三体微分对策模型指标函数；1.零控脱靶量矢量的定义原三体微分对策模型的系统方程包含七个微分方程，是七维的，后续求解需要进行多次积分，处理起来较为复杂。为了简化后续求解难度，定义新的状态变量矢量，即零控脱靶量矢量ZEM。ZEM的定义式如下：式中，z1、z2是ZEM的两个分量，z1是从当前时刻t到拦截时刻tf1，导弹和目标都不施加控制时，得到的导弹和目标之间的脱靶量，即零控脱靶量；z2是从当前时刻t到拦截时刻tf2，防御弹和导弹都不施加控制时，得到的导弹和防御弹之间的脱靶量；X是原三体微分模型的七维状态变量矢量；D是常系数矩阵；Φ(tf-t)是原三体微分对策模型的，从t时刻到tf时刻的状态转移矩阵，关于状态转移矩阵的概念可以参考现代控制理论相关书目；tf1、tf2分别是导弹和目标之间的拦截时刻、导弹和防御弹之间的拦截时刻；D矩阵为：状态转移矩阵可以通过下式进行求解：Φ(tf-t)＝L-1[(sI-A)-1](21)式中，I是7阶单位矩阵；A是原三体微分对策模型系统方程中的常系数矩阵(式(15))；s是频域变量；(sI-A)-1表示对矩阵(sI-A)求逆；L-1(·)表示拉普拉斯逆变换；将A的表达式(15)带入状态转移矩阵的计算式(21)中，可以得到状态转移矩阵的表达式为：将状态转移矩阵Φ(tf1-t)、Φ(tf2-t)，系数矩阵D以及原三体微分对策模型的状态变量矢量X(式(11))代入ZEM的定义式(19)中，可以得到ZEM的表达式如下：式中，tgo1是导弹和目标之间的剩余飞行时间，它等于拦截时刻tf1与当前时刻t之差；tgo2是导弹和防御弹之间的剩余飞行时间，它等于拦截时刻tf2与当前时刻t之差；tf1、tf2、aT、aM、aD、τT、τM、τD、yMT、yMD、θ0定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)的表达式为：式中，θT0、θD0、θM0的定义同步骤一；εT1、εD2、εM1、εM2及ψ(ε)函数的表达式如下：式中，tgo1、tgo2的定义同上；ε是任意变量；e是自然底数；2.新三体微分对策模型系统方程序号1定义了零控脱靶量矢量ZEM，它包含两个分量z1、z2，二者的表达式为式子(24)。分别将z1、z2对时间t求一阶导数，并结合微分方程组(13)，得到两个微分方程：式中，分别表示z1、z2对时间t的一阶导数；uM、uT、uD、θ0、δ的定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)的表达式同式(25)。这两个微分方程(式子(27))等价替换了原三体微分对策模型的系统方程(式子(14))，构成了新三体微分对策模型的系统方程。可以看出，原三体微分对策模型的系统方程包含7个微分方程，本步骤通过定义新的状态变量矢量ZEM后，只需要用2个微分方程就能够等价替换原7个微分方程，大大简化了后续求解难度。3.新三体微分对策模型指标函数根据零控脱靶量的物理意义可知，在拦截时刻，零控脱靶量就是实际交战的脱靶量，因此有下式成立：从而，原三体微分对策模型的指标函数(16)就可以等价替换为如下形式：式中，J′是与原指标函数(式子(16))等价的新指标函数，它是新三体微分对策模型的指标函数；z1(tf1)是z1在拦截时刻tf1对应的值，它和步骤一处的脱靶量yMT(tf1)是等价的；z2(tf2)是z2在拦截时刻tf2对应的值，它和步骤一处的脱靶量yMD(tf2)是等价的；uM、uT、uD、aMT、aMD、βT、βD、tf1、tf2定义同步骤一；本步骤中，序号2处的新三体微分对策模型的系统方程(式(27))，和序号3处新三体微分对策模型的指标函数(式(29))，共同组成了新三体微分对策模型。新模型是二维的，相比于原模型，形式上更简洁，后续求解也更加简单。步骤三：基于最优控制理论求解新三体微分对策模型，得到导弹的最优控制律；包括新三体微分对策模型的哈密顿函数、新三体微分对策模型对应的最优控制问题的求解；1.新三体微分对策模型的哈密顿函数新三体微分对策模型实际上是双边最优控制问题，导弹期望指标函数最大，即maxJ′，目标和防御弹组合则期望指标函数最小，即minJ′，这是一个典型的双边最优控制问题。要求解该最优控制问题，首先需要建立模型所对应的哈密顿函数。根据最优控制理论相关知识，新三体微分对策模型所对应的哈密顿函数为：将的表达式(27)带入式(30)，可得到本模型对应的哈密顿函数，具体如下：式中，H是新三体微分对策模型所对应的哈密顿函数；λ1、λ2分别是与相关的协态变量；的定义同步骤二；uM、uT、uD、βT、βD的定义同步骤一。2.基于最优控制理论求解新三体微分对策模型所对应的最优控制问题新三体微分对策模型实际上是双边最优控制问题，对该问题，最优控制理论给出了具体的求解方法。下面基于最优控制理论，求解新三体微分对策模型对应的最优控制问题，如下：在最优控制理论中，协态方程反映的是哈密顿函数对状态量的偏导数与协态变量对时间一阶导数的关系，具体为：式中，X是任意最优控制问题的状态变量矢量，表示哈密顿函数对状态变量的偏导数。对于本问题，状态变量矢量是ZEM，它包含状态变量是z1、z2，哈密顿函数的表达式如式子(31)，代入协态方程(32)中，可得：式中分别是协态变量λ1、λ2对时间的导数；分别表示哈密顿函数H对状态量z1、z2的偏导数，z1、z2分别是导弹和目标之间的零控脱靶量、导弹和防御弹之间的零控脱靶量，具体可以参见(19)；由于哈密顿函数H(式子(31))不显含状态量z1、z2，故：从而有：在最优控制理论中，将指标函数中与终端状态相关项记为是终端时刻tf和终端状态X(tf)的函数。横截条件反映的是协态变量的终端值和与对应状态变量偏导数的关系，具体为：针对本问题的指标函数(29)，可以写出函数的表达式为：再根据本问题的函数(式(36))，可以得到本问题的横截条件，如下：式中，表示函数对状态量z1、z2的偏导数。代入的表达式(36)，得到λ1、λ2在拦截时刻的值(即终端值)，如下：λ1(tf1)＝-αMTz1(tf1)，λ2(tf2)＝αMDz2(tf2)(38)式中，λ1(tf1)是协态变量λ1在拦截时刻tf1对应的值；λ2(tf2)是协态变量λ2在终端时刻值tf2对应的值；tf1、tf2的定义同步骤一；z1(tf1)、z2(tf2)的定义同步骤二；aMT、aMD的定义同步骤一；根据协态方程结果(式子(34))和λ1(tf1)、λ2(tf2)的表达式(38)，可得到协态变量λ1、λ2的表达式为：λ1＝-αMTz1(tf1)，λ2＝αMDz2(tf2)(39)式中，z1(tf1)、z2(tf2)的定义同步骤二；aMT、aMD的定义同步骤一；在最优控制理论中，耦合方程反映的是哈密顿函数与控制量的关系，当控制量使得哈密顿函数取得极值时，即为最优控制律，耦合方程表达式为：式中，u是任意最优控制问题的控制量矢量。对于本问题，控制量矢量u＝[uT；uD；uM]，即本问题的耦合方程为：式中，分别表示哈密顿函数H对控制量uM、uT、uD的偏导数；uM、uT、uD是交战三方的指令加速度，也即三者的控制量；将本模型对应的哈密顿函数H的表达式(31)代入耦合方程(41)，即可得到如下方程组：代入λ1、λ2表达式(39)，就可以得到交战三方的最优控制律，最优控制律的表达式如下：式中，分别是导弹、目标、防御弹的最优控制律；aMT、aMD、βT、βD、θ0、δ的定义同步骤一；fT(t)、fD(t)、fM1(t)、fM2(t)、z1(tf1)、z2(tf2)的定义同步骤二；可以发现三者的最优控制律均是z1(tf1)、z2(tf2)的显示表达式，然而，在实际交战中，并不知道终端时刻的零控脱靶量值z1(tf1)、z2(tf2)，只能够通过当前交战双方的信息计算当前时刻的零控脱靶量z1(t)、z2(t)，因此，很有必要建立z1(t)、z2(t)和z1(tf1)、z2(tf2)的显示关系。将三者的最优控制律(式(43))代入新三体微分对策模型的系统方程(27)中，得到将得到的微分方程在[t，tf1]内对时间积分，且考虑阶跃函数δ的表达式(12)，以及，导弹和防御弹的交战完成时刻要先于导弹和目标的交战完成时刻这一假设，即tf2＜tf1。得到关于z1(tf1)、z2(tf2)的线性方程组，如下：系数矩阵K的表达式如下：式中，gMT、gMD、kMT、kMD的表达式为：式中，aMT、aMD、βT、βD、θ0定义同步骤一；εT1、εD2、εM1、εM2的定义同步骤二；h(εT1)、h(εM1)、h(εD2)、h(εM2)、h′(εM2)的表达式如下：式中，εT1、εD2、εM1、εM2、函数ψ(ε)的定义同步骤二；θT0、θD0、θM0、τT、τD、τM的定义同步骤一；函数k1(ε)、k2(ε)、k3(ε)、g(ε)、ΔεM表达式如下：式中ε为任意变量；e为自然底数；tf1、tf2是拦截时刻，二者的定义同步骤一；根据克莱姆法则，对上述线性方程组(45)进行求解，得到z1(tf1)、z2(tf2)的表达式如下：式中，z1(tf1)是导弹和目标在拦截时刻tf1时的零控脱靶量，z2(tf2)是导弹和防御弹在拦截时刻tf2时的零控脱靶量，z1是导弹和目标在当前时刻的零控脱靶量，z2是导弹和防御弹在当前时刻的零控脱靶量；Δ是系数矩阵K的行列式；Δ11、Δ12、Δ21、Δ22分别是行列式Δ对应下标元素的代数余子式，如Δ12表示行列式Δ对应第1行第2列元素的代数余子式。将z1(tf1)、z2(tf2)的表达式代入(50)导弹的最优控制律(43)中，并进行整理，得到导弹的最优控制律即是一种微分对策反拦截机动突防/精确打击导引方法；式中，第一项用于导引导弹拦截目标，即落点精度控制作用，第二项用于导引导弹规避防御弹的拦截，即起突防作用。tgo1、tgo2、z1、z2的定义同步骤二；NM1是关于零控脱靶量z1的有效导航系数；NM2是关于零控脱靶量z2的有效导航系数，NM1、NM2的表达式为：式中，aMT、aMD、tgo1、tgo2、θ0的定义同步骤一；tgo1、tgo2、fM1(t)、fM2(t)的定义同步骤二；Δ11、Δ12、Δ21、Δ22、Δ的定义式(50)；上述三个步骤中，步骤一是根据交战三方的动力学环节和线性化相对运动学模型建立三体对抗微分对策模型；考虑到步骤一的三体微分对策模型是七维的，求解难度较大，步骤二对其进行了处理，通过零控脱靶量矢量将原七维问题降阶成二维问题，得到了新的三体微分对策模型；步骤三是基于最优控制理论，对新三体微分对策模型所对应的双边最优控制问题进行求解，得到导弹的最优控制律，该最优控制律即是一种微分对策反拦截机动突防/精确打击导引方法。通过上述三个步骤，描述了三体微分对策模型的建立过程、新旧模型的转换过程以及微分对策模型的求解过程，最终得到了一种微分对策反拦截机动突防/精确打击导引方法。实施案例为了检验所提机动策略的效果，针对巡航导弹攻击水面目标案例，进行数值仿真校验。巡航导弹攻击水面目标，水面目标方发射防御弹对巡航导弹进行拦截，防御弹采用的导引律为PN，有效导航比取3。在本案例中，巡航导弹对应着本发明中所述的导弹，字母为M，水面目标对应着本发明中所述的目标，字母为T，防御弹对应着字母D。上面在推到本发明方法时，假设交战模型可以沿着各自对应的初始碰撞三角形进行线性化处理。仿真中为了更加贴近实际交战情形，用到的交战模型是二维非线性模型，首先根据图2几何关系，可以写出如下相对运动学方程组假设交战三方的实际加速度方向均垂直于各自的速度方向，则有如下动力学方程组式(53)～(54)中的相关参数的定义同“具体实施方式”一节。仿真用到的软件是matalb2011a，仿真过程中的参数设置如表1所示，表中，下标0表示对应量的初始值；单位g表示重力加速度常量，取为9.8m/s2，单位中m表示米，s表示秒；其他参数、单位的定义同技术方案中所定义的，表中单位deg表示角度。弹道积分方法采用四阶龙格库塔法，积分步长0.01s，s表示秒。首先，针对上述巡航导弹攻击水面目标案例，巡航导弹分四种方案实施。方案一是巡航导弹前期不进行机动突防，直接采用PN攻击水面目标；方案二是巡航导弹先采用蛇形机动进行突防，期望规避防御弹的拦截，蛇形机动角频率取4rad/s(rad表示弧度，s表示秒)，初始相位π/2，再采用PN攻击水面目标；方案三巡航导弹先采用最优机动进行突防，再采用PN攻击水面目标；方案四采用本发明方法，进攻机动突防和精确打击。上述PN的有效导航比均取3。图3～图6是四种方案对应的弹道曲线，表2是四种方案对应的仿真结果结果，突防脱靶量是指巡航导弹突防防御弹时对应的脱靶量；落点偏差是指巡航导弹打击目标时的脱靶量。方案一中，因巡航导弹没有采取机动突防措施，而被防御弹精确拦截(突防脱靶量0.1663m)，造成任务失败(三者的弹道曲线如图3)。方案二中，巡航导弹采用了蛇形机动进行突防，但由于蛇形机动是一种程序式的机动，突防概率较低，使得巡航导弹突防防御弹的脱靶量仍然较小(2.6297m)，被防御弹成功拦截(三者的弹道曲线如图4)。方案三中，巡航导弹采用了最优机动进行突防，由于最优机动具有实时最优性，其突防概率高，使得巡航导弹成功地规避了防御弹的拦截，脱靶量达到36.6431m。但是在突防过程中，巡航导弹和水面目标之间的偏差积累较大，后期采用PN攻击水面目标时，未能命中目标，落点偏差达到376.6184m，任务失败(三者的弹道曲线如图5)。方案四中，巡航导弹采用本发明进行突防和攻击，其突防防御弹的脱靶量较大，达到11.2019m，同时，前期的突防过程并未为后期攻击水面目标阶段带来不利影响，后期能够实现对水面目标的精确打击，落点偏差仅为0.2734m(三者的弹道曲线如图6)表1仿真参数设置参数取值参数取值VM0/(m/s)300τM/(s)0.2VT0/(m/s)25τT/(s)--VD0/(m/s)400τD/(s)0.2aMmax/(g)5γM0/(deg)-8.2aTmax/(g)0γT0/(deg)0aDmax/(g)8γD0/(deg)8.2RMT0/(m)2010λMT0/(deg)5.7RMD0/(m)2010λMD0/(deg)5.7aMT105βT105aMD108βD0.95进一步，考虑巡航导弹不同机动能力条件下，本发明的突防效果和落点精度控制效果。图7是巡航导弹具有不同机动能力条件下的弹道曲线族，图8是对应的巡航导弹突防防御弹的脱靶量曲线以及攻击水面目标的落点偏差曲线。可以看出，当巡航导弹的机动能力变强时，其弹道“拉起”幅度越大，突防防御弹的脱靶量越大，攻击水面目标时落点偏差越小，实现了反拦截机动突防和精确打击一体化。表2各方案脱靶量和落点偏差结果仿真结果方案一方案二方案三方案四无机动+PN蛇形机动+PN最优机动+PN本发明突防脱靶量/(m)0.16632.629736.643111.2019落点偏差/(m)0.02680.1029376.61840.2734综上所述，通过上述步骤，推到出了本发明方法，即一种微分对策反拦截机动突防/精确打击导引方法，案例仿真结果表明本发明方法比传统的程序式机动方式脱靶量大，能够提高导弹自身的生存概率，且比最优机动方式的落点偏差小，能够提高导弹的命中精度，综合性能优异。当前第1页1 2 3