基于量子小波神经网络模型的脑电波情绪认知方法与流程

本发明涉及一种脑电波的情绪认知方法，特别是一种基于量子神经网络和小波理论相结合的脑电波数据情绪认知方法。

背景技术：

近些年来，一些新形式的数字媒体与人体的交互在娱乐，学习等领域有着巨大的潜力和市场。然而情绪在人类的生活中扮演着重要的角色，所以在计算机接口的应用中，基于情绪认知的需求与日俱增。人类有六种基本的情绪，即快乐、悲伤、恐惧、惊讶、愤怒、嫉妒。这六种情绪可以相互组合，并派生出其余各种各样的复合情绪，如忧郁、紧张、焦虑等。情绪认知是人工智能、人机交互等领域的关键技术。信息时代的来临，要求机器能够更友好的理解和表达人类的情绪，在现实生活中，情绪认知已经应用到医疗、教育、商业等领域，但是由于情绪是一个非常复杂的认知过程，情绪认知若想取得较好效果，有赖于不断深入的研究。脑电信号是一种电生理信号，具有客观性和精确性，能直接反映大脑的活动，因而被广泛应用到情绪认知中。

脑电波(electroencephalogram，eeg)与情绪有着紧密的联系，脑电波是大脑在活动时，大量神经元同步发生的突触后电位经总和后形成的。它记录大脑活动时的电波变化，是脑神经细胞的电生理活动在大脑皮层或头皮表面的总体反映，其频率变动范围在每秒1－30次之间，可划分为四个波段，即δ(1－3hz)、θ(4－7hz)、α(8－13hz)、β(14－30hz)。其中，α指数(即α波占全部脑波百分比，安静、闭目时α指数为75％)可以作为情绪表现的指标，情绪稳定而思维广博的人，α指数较高，情绪不稳定而狭隘偏激的人α指数则甚低。α波易受外界刺激干扰，在睁眼时，α波会减弱或消失，即便是在黑暗的环境中，睁眼也会如此。β波不受睁、闭眼的影响。在睁眼视物、情绪紧张、焦虑不安、惊疑恐惧或服用安定等药物时，β波活动急剧增多。β活动也与人的某些心理品质有关。β节律优势的人常表现为：精神紧张、情绪不稳、感情强烈、易于冲动、固执己见的特点。除此之外，在觉醒并专注于某一事时，常可见一种频率较β波更高的γ波，其频率为30～80hz，波幅范围不定；而在睡眠时还可出现另一些波形较为特殊的正常脑电波，如驼峰波、σ波、λ波、κ-复合波、μ波等。

目前脑电波的采集主要采用脑机接口的方式，脑机接口(brain-computerinterface，bci)，有时也称作“大脑端口”directneuralinterface或者“脑机融合感知”brain-machineinterface，它是在人或动物脑(或者脑细胞的培养物)与外部设备间建立的直接连接通路。在单向脑机接口的情况下，计算机或者接受脑传来的命令，或者发送信号到脑(例如视频重建)，但不能同时发送和接收信号。而双向脑机接口允许脑和外部设备间的双向信息交换。

量子神经网络(quantumneuralnetwork，qnn)是量子计算和神经网络理论相结合产生的新的计算模型，是当今新兴的前沿交叉学科之一。量子神经网络将量子计算的基本概念和原理引入到神经网络模型中，对传统神经网络模型进行量子化改造，从而增强神经网络的性能和速度，为神经网络的进一步发展提出了新的思路。量子神经网络在eeg信号的情绪认知方面，弥补了之前采用传统神经网络来进行eeg信号情绪认知的不足，具有高稳定，高精度及快速收敛等特点。

但目前，量子神经网络计算的eeg情绪认知不仅效率低，而且精度并不高。

针对上诉问题，本发明人设计了速度更快、精度更高的基于量子小波神经网络模型的脑电波情绪认知方法。

技术实现要素：

本发明的目的在于提供基于量子小波神经网络模型的脑电波情绪认知方法，实现更快的收敛速度和更高的认知精度。

为了实现上述目的，本发明采用如下技术方案：

基于量子小波神经网络模型的脑电波情绪认知方法，包括以下步骤：

步骤一，将采集的脑电波数据集进行正则化，正则化后的值在0到1之间；

步骤二，对正则化后的数据进行预处理，具体是采用独立主成分分析法(ica)将干扰数据从脑电波数据中移除；

步骤三，对预处理后的数据进行特征提取，具体采用聚类技术(ct)通过选择特定的特征来减小数据集的大小；

步骤四，采用三层前向型量子小波神经网络(qwnn)对数据进行分类，其中量子小波神经网络的隐层适应基函数采用mexican-hat小波函数，该函数具体的表达式为：

其中t为时间变量；

步骤五，进行评价值唤醒程度分析。

采用所述独立主成分分析法移除干扰数据具体包括以下步骤：

(1)将步骤一中正则化的数据记为k2(t),k3(t)...kn(t)并与期望信号k1(t)一起作为输入信号k(t)＝[k1(t)；k2(t)；k3(t)；...kn(t)]进行独立主成分分析，得到分离信号s(t)＝[s1(t)；s2(t)；s3(t)；...sn(t)]；

(2)将分离信号分别进行频谱分析，根据理想信号s'(t)特征确定目标信号s1(t)；

(3)采用频谱校正法对独立主成分分析后的分离信号s1(t)进行频谱恢复，最后得到去除干扰信号的y(t)信号。

采用所述聚类技术(ct)进行特征提取的步骤包括：

1)将每个脑电波数据分割为n个组，各组称为特殊的时间间隔簇；

2)把每个簇划分为m个特殊期间的子簇；

3)从每个子簇的数据点中提取八个统计特征，这些脑电波数据的统计特征分别是：最小值，最大值，均值，中值，第一四分位范围，第三四分位范围，四分位全距和标准差。

所述三层前向型量子小波神经网络的训练包括以下步骤：

①、将所有的训练输入向量输入到量子小波神经网络，量子小波神经网络采用三层前向型神经网络，输入层包含ni个节点，隐层包含nh个多层节点，输出层包含no个节点。wjl表示第l个输入节点到第j个隐层节点的权值，vij表示第j个隐层节点到第i个输出层节点的权值。记

这里m表示数据集x的期望向量的数目；假设一个多层隐层节点有ns个离散的量子层，则激励函数可以写成由ns个子激励函数的叠加，并由θ^s进行转换，其假设模型的具体表达式如下：

其中，表示隐层节点的激励函数，β表示斜率参数，θ^s表示量子间隔，λj表示伸缩因子，τj表示转移因子；

输出层的输出向量为：

其中

qwnn模型的一般表达式为：

其中k表示样本的数量；

②、qwnn权值的更新：

代价函数为其中k＝1，2，...，m，m是训练样本总数，参数wjl，vij，λj，τj通过最小化代价函数来进行更新：

其中

对于任何h次迭代，参数wjl，vij，λj，τj都根据下式进行调整：

其中α是学习率，0<α<1。

③、量子间隔的更新：

ci类的输出方差为：

其中，表示属于类ci的隐层节点的输出总和。

量子间隔通过最小化代价函数g来进行调整：

计算g的梯度：

其中αθ为的学习率，0<αθ<1；

其中，

令

最后计算其更新方程：

根据下式进行更新：

所述步骤五进行评价值唤醒程度分析，具体为：

通过改变面部肌肉的控制参数，定义六个haptek情绪因子，这些情绪因子分别是：快乐、悲伤、恐惧、惊讶、愤怒、嫉妒，这些情绪因子已通过步骤四所述算法进行了分类；

做评价值及唤醒程度的映射，其中唤醒程度只能从标记的0,1,2中选取，而评价值只能从标记的0和1中选取。

采用上述方案后，本发明有益效果是：将小波理论运用于量子神经网络算法，对量子神经网络算法进行了改进，得到了量子小波神经网络算法，并运用于脑电波的情绪认知中，在处理eeg情绪认知方面，量子小波神经网络算法与传统的神经网络和量子神经网络算法相比而言，具有更快的收敛速度和更高的精度。

下面结合附图对本发明做进一步的说明。

附图说明

图1为本发明脑电波数据处理流程图。

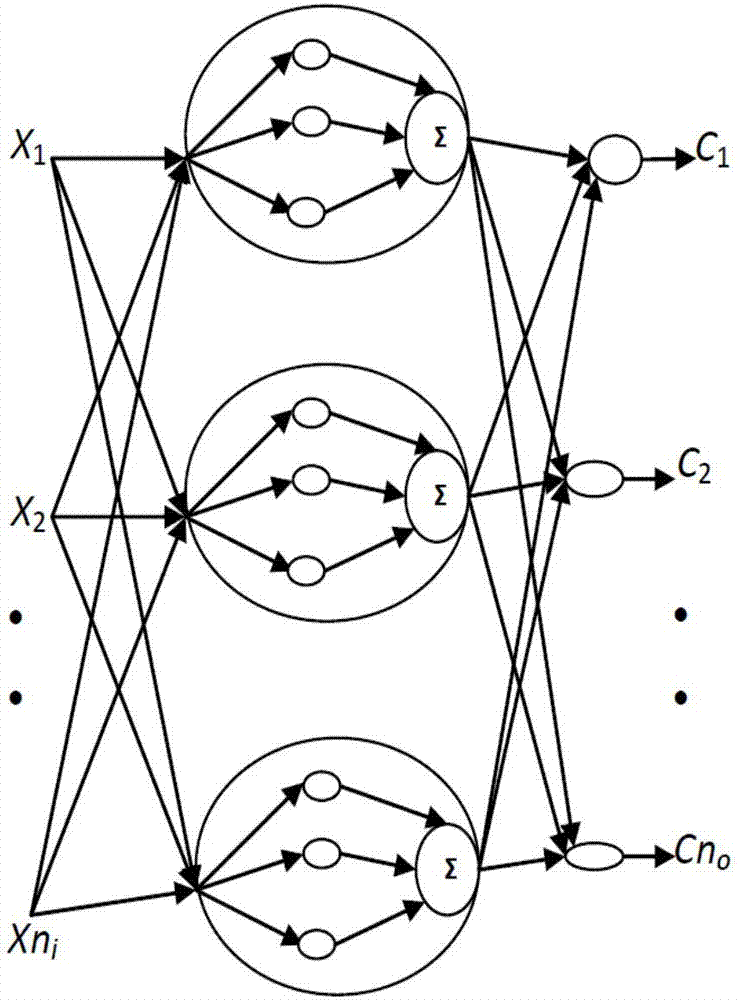
图2为本发明量子小波神经网络结构图。

图3为六大基本情绪在唤醒程度-评价值坐标的标记。

具体实施方式

如图1所示本实施例揭示的基于量子小波神经网络模型的脑电波情绪认知方法，具体包括以下步骤：

步骤一，将采集的脑电波数据集进行正则化，正则化后的值在0到1之间；

步骤二，对正则化后的数据进行预处理，具体是采用独立主成分分析法(ica)将干扰数据从脑电波数据中移除，干扰数据主要是噪音数据；

采用所述独立主成分分析法移除干扰数据具体包括以下步骤：

(1)将步骤一中正则化的数据记为k2(t),k3(t)...kn(t)并与期望信号k1(t)一起作为输入信号k(t)＝[k1(t)；k2(t)；k3(t)；...kn(t)]进行独立主成分分析，得到分离信号s(t)＝[s1(t)；s2(t)；s3(t)；...sn(t)]；

(2)将分离信号分别进行频谱分析，根据理想信号s'(t)特征确定目标信号s1(t)；

(3)采用频谱校正法对独立主成分分析后的分离信号s1(t)进行频谱恢复，最后得到去除干扰信号的y(t)信号。

步骤三，对预处理后的数据进行特征提取，具体采用聚类技术(ct)通过选择特定的特征来减小数据集的大小；

采用所述聚类技术进行特征提取的步骤包括：

1)将每个脑电波数据分割为n个组，各组称为特殊的时间间隔簇；

2)把每个簇划分为m个特殊期间的子簇；

3)从每个子簇的数据点中提取八个统计特征，这些脑电波数据的统计特征分别是：最小值，最大值，均值，中值，第一四分位范围，第三四分位范围，四分位全距和标准差。

步骤四，采用三层前向型量子小波神经网络(qwnn)对数据进行分类，其中量子小波神经网络的隐层适应基函数采用mexican-hat小波函数，该函数具体的表达式为：

其中t为时间变量；

步骤五，进行评价值唤醒程度分析。

步骤五进行评价值唤醒程度分析，具体为：

通过改变面部肌肉的控制参数，定义六个haptek情绪因子，这些情绪因子分别是：快乐、悲伤、恐惧、惊讶、愤怒、嫉妒，这些情绪因子已通过步骤四所述算法进行了分类；

做评价值及唤醒程度的映射，其中唤醒程度只能从标记的0,1,2中选取，而评价值只能从标记的0和1中选取，映射结构参见图3。

步骤四中，三层前向型量子小波神经网络的训练包括以下步骤：

①、将所有的训练输入向量输入到量子小波神经网络，如图2所示，量子小波神经网络采用三层前向型神经网络，输入层包含ni个节点，隐层包含nh个多层节点，输出层包含no个节点。wjl表示第l个输入节点到第j个隐层节点的权值，vij表示第j个隐层节点到第i个输出层节点的权值。记

这里m表示数据集x的期望向量的数目；假设一个多层隐层节点有ns个离散的量子层，则激励函数可以写成由ns个子激励函数的叠加，并由θ^s进行转换，其假设模型的具体表达式如下：

其中，表示隐层节点的激励函数，β表示斜率参数，θ^s表示量子间隔，λj表示伸缩因子，τj表示转移因子；

输出层的输出向量为：

其中

qwnn模型的一般表达式为：

其中k表示样本的数量；

②、qwnn权值的更新：

代价函数为其中k＝1，2，...，m，m是训练样本总数，参数wjl，vij，λj，τj通过最小化代价函数来进行更新：

其中

对于任何h次迭代，参数wjl，vij，λj，τj都根据下式进行调整：

其中α是学习率，0<α<1。

③、量子间隔的更新：

ci类的输出方差为：

其中，表示属于类ci的隐层节点的输出总和。

量子间隔通过最小化代价函数g来进行调整：

计算g的梯度：

其中αθ为的学习率，0<αθ<1；

其中，

令，

最后计算其更新方程：

根据下式进行更新：

上述说明示出并描述了本发明的优选实施例，应当理解本发明并非局限于本文所披露的形式，不应看作是对其他实施例的排除，而可用于各种其他组合、修改和环境，并能够在本文发明构想范围内，通过上述教导或相关领域的技术或知识进行改动。而本领域人员所进行的改动和变化不脱离本发明的精神和范围，则都应在本发明所附权利要求的保护范围内。