基于分子动力学的铅铋快堆裂变产物扩散系数求解方法

本发明涉及核反应堆燃料中裂变产物扩散行为研究，具体涉及一种基于分子动力学的铅铋快堆裂变产物扩散系数求解方法。

背景技术：

1、铅铋快堆是指以液态铅铋合金为冷却剂的一种反应堆，其作为第四代反应堆中的一种，因其所具有的安全性、高中子经济型、可持续发展性和自然循环能力等特点，备受广大研究人员的重视。然而uo2燃料的结构特征和材料特性之间的复杂物理关系且相互关联，元素扩散组分多，致使裂变产物扩散过程十分复杂，难以通过实验开展全面的化学相互作用研究。因此需要基于数值模拟方法，采用分子动力学对不同温度下的元素扩散机制进行研究，获取基于不同温度条件下的元素扩散模型。

2、分子动力学(md)是一门结合物理、数学和化学的综合模拟方法，该方法基于牛顿力学描述分子体系的运动，用于模拟一个到几个晶粒尺度下的结构演化，通过统计力学获取有关的各种物理性质的信息。其主要分为经典分子动力学、第一性原理分子动力学。其中经典分子动力学用经验势来描述体系的力场，其中包含一些经验参数，这些经验参数可以通过量子力学计算确定，也可以通过拟合实验数据获得。由于其采用经验势来描述力场，其计算量相较于第一性原理分子动力学大大减少，因此可以处理庞大的体系。采用分子动力学精确模拟计算扩散系数，往往需要庞大的分子体系和较长的时间模拟计算，因此采用经典分子动力学，能够从分子水平去研究裂变产物在燃料中的扩散行为，计算出裂变产物在不同温度条件下的扩散系数，为其它裂变产物扩散行为的研究提供基础数据与帮助。

技术实现思路

1、为了研究裂变产物在燃料中的扩散行为，揭示裂变产物在燃料中的扩散过程可能存在的一些现象，本发明基于经典分子动力学，通过实验或采用第一性原理拟合获取经验势，提出一种基于分子动力学的铅铋快堆裂变产物扩散系数求解方法，该方法适用于铅铋快堆芯块内裂变产物在基体材料中的扩散系数计算，能够在分子水平上计算不同裂变产物在铅铋快堆芯块不同温度条件下的扩散系数，为进一步的裂变产物扩散行为的计算、分析与探究提供基础数据与帮助。

2、为了实现上述目的，本发明采取了以下的技术方案予以实施：

3、一种基于分子动力学的铅铋快堆裂变产物扩散系数求解方法，其特征在于：步骤如下：

4、步骤1：首先获取铅铋快堆芯块的晶胞类型和晶格常数，然后采用建模软件建立铅铋快堆芯块的晶胞模型，以供分子动力学软件使用；

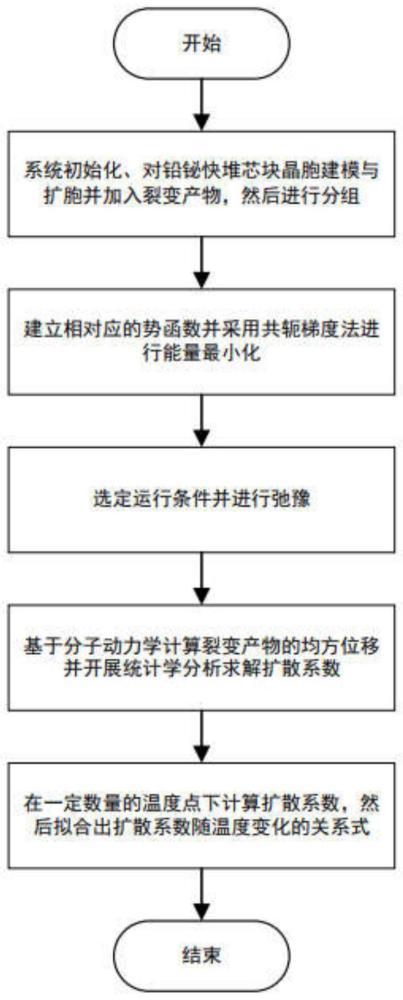
5、步骤2：将分子动力学软件系统初始化，选取适配单位制、模拟粒子类型，再将边界条件设定为三向周期性边界；

6、步骤3：读取建立的铅铋快堆芯块的晶胞模型，在正交方向上复制晶胞若干次并去除原子以形成缺陷，并将裂变产物原子填充到这些缺陷中，形成铅铋快堆芯块-裂变产物扩散系数计算模型；

7、步骤4：将裂变产物和铅铋快堆芯块的原子各分为一组，裂变产物原子组用于后续计算裂变产物在铅铋快堆芯块中的均方位移msd以及裂变产物扩散行为的分析，基体材料原子组用于观测运算中是否存在问题；

8、步骤5：针对裂变产物在铅铋快堆芯块中的扩散模拟，建立相对应的人工势场——势函数，通过实验、基于量子力学原理的计算拟合获取势函数的关键势参数，并将关键势参数以势函数所要求的格式写成势函数文件供分子动力学软件使用，以模拟裂变产物原子与铅铋快堆芯块原子之间的相互作用，以及两者自身原子之间的相互作用；建立的势函数有buckingham势函数、lj势函数、morse势函数；buckingham势函数、lj势函数、morse势函数的公式分别如公式(1)、(2)、(3)所示；

9、buckingham势函数：

10、式中，

11、v(r)表示两个粒子的相互作用势能；

12、a表示排斥项的强度；

13、ρ表示排斥参数；

14、c表示吸引项的强度；

15、r表示两个粒子中心之间的距离；

16、lj势函数：

17、式中，

18、v(r)表示两个粒子的相互作用势能；

19、ε表示势能的深度；

20、σ表示两个粒子势能为零时的距离；

21、r表示两个粒子中心之间的距离；

22、morse势函数：

23、式中，

24、v(r)表示两个粒子的相互作用势能；

25、d0表示势能的深度；

26、α表示控制振频的参数；

27、r0表示平衡距离；

28、步骤6：采用共轭梯度法对裂变产物和铅铋快堆芯块进行能量最小化，将裂变产物和铅铋快堆芯块的分子结构优化为能量最优结构，防止原子之间距离过近导致排斥力极大破坏模拟运算的进行；

29、步骤7：以一个原子为最小单位基于牛顿经典力学原理计算所有原子的运动状态，首先选取运行步长并采用velocity-verlet算法计算牛顿运动方程中的时间积分，然后对整个热扩散模拟系统施加一定的初速度，并采用正则系综和nose-hoover恒温方法保持裂变产物和铅铋快堆芯块的温度恒定，用于后续弛豫与均方位移计算过程；

30、步骤8：在步骤7所选定的恒温温度下弛豫裂变产物在铅铋快堆芯块中的热扩散模拟系统，使热扩散模拟系统达到热力学平衡状态；

31、步骤9：在正则系综下恒温运行一定时间，通过计算裂变产物所有粒子在若干个步长之后的位置与初始位置的差的绝对值的平方，再将上述的所有数据做加和再求平均值，以此方法计算得到裂变产物在铅铋快堆芯块中的均方位移msd，计算公式如公式(4)所示，然后将裂变产物在铅铋快堆芯块中的均方位移msd数据记录下来，方便后续提取数据；

32、

33、式中

34、msd表示裂变产物在铅铋快堆芯块中的均方位移,

35、n表示裂变产物粒子的个数；

36、ri(t)表示在模拟时刻t时第i个原子的位置，埃米

37、ri(0)表示在初始时刻0时第i个原子的位置，

38、步骤10：提取裂变产物在铅铋快堆芯块中的均方位移msd数据，去除msd增长较快的部分，然后计算剩余部分的msd数据的平均值<msd>，之后基于均方位移结果开展统计学分析计算求解扩散系数，具体采用如公式(5)所示的统计学公式计算扩散系数d；

39、

40、式中

41、d表示扩散系数，m2/s；

42、<msd>表示剩余部分的msd的平均值，

43、n表示热扩散模拟系统的维数；

44、t表示平均时间，皮秒ps；

45、步骤11：选定温度区间，选定该温度区间内一定数量的温度点，根据步骤1到步骤10计算得出一定数量选定温度点的扩散系数；

46、步骤12：采用arrhenius方程表示扩散系数随温度变化的曲线关系，见公式(6)所示，使用步骤11中计算得出的一定数量选定温度点的扩散系数，以一定数量的散点来拟合曲线的方式，获取整个温度区间内扩散系数随温度变化的表示式，即公式(6)，其中levenberg-marquardt算法被用来拟合扩散前因子d0和活化能ea；

47、

48、式中

49、d表示扩散系数，m2/s；

50、d0表示扩散前因子，m2/s；

51、ea表示活化能，ev；

52、k表示玻尔兹曼常数，j/k；

53、t表示运行温度，k；

54、通过以上步骤，模拟了裂变产物在铅铋快堆芯块内的扩散过程，得到了裂变产物分子在铅铋快堆芯块内的均方位移，并计算出扩散系数在一定温度范围内随温度变化的表达式，从而能够为裂变产物在燃料中的扩散过程的机理性研究提供基础数据和帮助。

55、和现有技术相比较，本发明具备如下优点：

56、1、该方法建立了铅铋快堆芯块-裂变产物扩散系数数值计算模型，可以对裂变产物在铅铋快堆芯块内的扩散系数进行计算；

57、2、该方法提供了在原子尺度上观察裂变产物扩散行为的可能性，能够揭示裂变产物与燃料芯块之间的相互作用机制；

58、3、由于步骤3铅铋快堆芯块可以根据研究目的调整其状态与性质，裂变产物可以调整其数量与种类，该方法可以处理多组分体系，例如含有多种裂变产物、缺陷、氧化物的燃料芯块；

59、4、由于步骤7可以根据研究目的调整运行条件，并且模拟运算较之实验而言不会受到设备条件的限制，该方法可以计算极端的温度压力工况条件，从而获得更为精确的扩散系数。

60、综上，本发明能够使用更加经济、更加微观的方法去计算更加复杂、条件更加极端的裂变产物在铅铋快堆芯块内的扩散系数。