基于实验数据重正化库伦定律的方法与流程

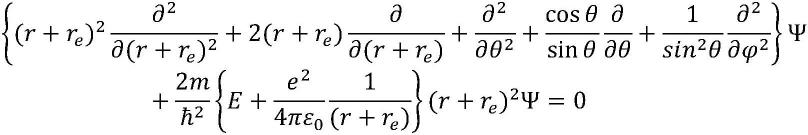
1.本发明涉及一种基于实验数据重正化库伦定律的方法。


背景技术：

2.库仑定律(coulomb’s law)是静止点电荷相互作用力的规律，1785年法国科学家c，-a.de库仑由实验得出，库仑定律的常见表述：
3.真空中两个静止的点电荷之间的相互作用力，与它们的电荷量的乘积(q1q2)成正比，与它们的距离(数学距离)的二次方(r2)成反比，作用力的方向在它们的连线上，同性电荷相斥，异性电荷相吸。即：
[0004][0005]
与万有引力定律类似，现有的库伦定律也存在一个明显的缺陷，就是在两个点电荷q1、q2之间的距离趋于零的情况下，电场力f
12
会趋于无穷大，但是，这明显与事实不符，也就是说，在两个点电荷q1、q2之间相距为零时，两个点电荷q1、q2之间的相互作用力f
12
也不可能是无穷大。事实上，即使两个点电荷q1、q2之间的距离趋于零，电场力f
12
也只能是趋于一个常数，绝不会是无穷大。
[0006]
现有的物理实验可以定性地证明，当二个点电荷q1、q2重合时，并没有释放出无穷大的能量，例如，正负电子对的湮灭反应，即是例证。
[0007]
因此，有必要现有的库伦定律进行重正化处理，重正化的方法是重新审视现有的库伦定律的分母项中的距离r项，将距离r段中位于中心点处的一段距离从利用库伦定律的数学计算中剔除掉，也就是从原点开始、在向外的方向上的间距折断下来一段长度，并对这段折断下来的间距做特别处理，要“另眼相看”这段折断间距，折断、剔除的方式是插入一个来自物理实验的常数，插入的基本原则是让库伦定律在两个点电荷q1、q2之间的距离趋于零的情况下，两个点电荷q1、q2之间的相互作用力f
12
不是无穷大。毋庸置疑，这一修正要最大限度地包容现有的库伦定律符合的平方反比定律这一实验事实，而不能违反这一实验结果。


技术实现要素：

[0008]
本发明的目的是提供一种可解决现有的库伦定律存在明显的缺陷，得到库伦定律中的场源最小常数re，计算出电子在其半径为零处的静电场的场强，从而更好的服务于各种涉及计算静电作用力大小的科技项目的基于实验数据重正化库伦定律的方法。
[0009]
本发明的基于实验数据重正化库伦定律的方法，其包括如下步骤：
[0010]
a、准备二个可带电量分别为q1和q2的物体；
[0011]
b、准备一个用于测量静电力常数的装置；
[0012]
c、让二个物体分别带上q1和q2的电量，不需要对其所带电量进行计量，利用所述的用于测量静电力常数的装置，测量二个物体之间的库伦力f1的大小，同时测量得到二个
物体之间的距离为r1，然后再改变二个物体之间的距离为r2，并再次测量出改变了二个物体之间的距离为r2后物体之间的库仑力f2的大小；
[0013]
e、根据修正后的库伦定律的其中一个如下形式的公式
[0014][0015]
将二次测量结果代入上式，分别得到：
[0016]
f1＝k q1q2/(r1+re)2ꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22)
[0017]
f2＝k q1q2/(r2+re)2ꢀꢀꢀꢀꢀꢀꢀꢀ
(23)
[0018]
简化式(22)、式(23)二个方程式，可得到：
[0019]
f1/f2＝(r2+re)2/(r1+re)2ꢀꢀꢀꢀ
(24)
[0020]
再将通过实验测量到的f1、f2和r1、r2代入(24)式，即可得出库伦定律中场源最小常数re的具体数值。
[0021]
优选的，所述用于测量静电力常数的装置为卡文迪许扭秤，所述的二个物体分别为采用金属制成的空心球形体。
[0022]
本发明的基于实验数据重正化库伦定律的方法，其包括准备二个可带电量分别为q1和q2的物体，准备一个用于测量静电力常数的装置，让二个物体分别带上q1和q2的电量，不需要对其所带电量进行计量，利用所述的用于测量静电力常数的装置，测量二个物体之间的库伦力f1的大小，同时测量得到二个物体之间的距离为r1，然后再改变二个物体之间的距离为r2，并再次测量出改变了二个物体之间的距离为r2后物体之间的库仑力f2的大小，再将通过实验测量到的f1、f2和r1、r2代入对应的计算公式，即可得出库伦定律中场源最小常数re的具体数值。因此，本发明的基于实验数据重正化库伦定律的方法可解决现有的库伦定律存在明显的缺陷，得到库伦定律中的场源最小常数re，计算出电子在其半径为零处的静电场的场强，从而更好的服务于各种涉及计算静电作用力大小的科技项目。
[0023]
下面对本发明的基于实验数据重正化库伦定律的方法的具体实施方式作进一步详细说明。
具体实施方式
[0024]
牛顿的普适的万有引力定律表示如下：
[0025]
任意两个质点m1、m2由通过连心线方向上的力f
12
相互吸引，该引力f
12
大小与它们质量的乘积m1m2成正比，与它们之间距离r的平方成反比，与两物体的化学组成和其间介质种类无关。
[0026][0027]
现有的万有引力定律存在一个明显的缺陷，就是在两个质点m1、m2之间的距离r趋于零的情况下，引力f
12
会趋于无穷大，或者说质点的原点(奇点)所在处的引力场场强是无穷大。但是，现有的物理实验可以定性地证明，当二个质点重合时，并没有释放出无穷大的能量，例如，正负电子对的湮灭反应，即是例证。其他的实验证据还有：黑洞对外界物质的吸引作用，也可以证明落入黑洞奇点内的外界物质不会受到物理上的无穷大的引力作用。
[0028]
基于两个质点m1、m2之间的距离r趋于零，所释放出的能量为有限值这一事实，我们有理由假设此种情况下两个质点m1、m2之间的引力f
12
是趋于一个常数，不是趋于无穷大。此
外，如果质点的原点所在处的引力场的场强是物理上的无穷大，那么，即使离开了质点的原点(奇点)进行检测，该无穷大的引力场场强也不会因为有了距离r而有丝毫的递减，其依然只能是无穷大。
[0029]
鉴于我们有足够多的实验可以证明，在离开了质点的原点(奇点)处进行引力场场强的检测时，引力场的场强依然是一个有限的物理量。因此，需要从实验出发，对现有的万有引力定律进行重正化处理，让基于万有引力定律推导出来的引力场的场强不会出现无穷大的结论。为此，需要基于物理实验的数据，对现有的万有引力定律进行修正，以解决其在两个质点m1、m2之间的距离趋于零时出现的无穷大难题。毋庸置疑，这一修正要最大限度地包容现有的万有引力定律符合的平方反比定律这一实验事实，而不能违反这一实验结果。
[0030]
基于上述要求，可对现有的万有引力定律进行重正化的方案，是重新审视现有的万有引力定律的分母项中的距离r项，将距离r段中位于中心点处的一段距离从利用万有引力定律的数学计算中剔除掉，也就是从原点开始、在向外的方向上的间距折断下来一段长度，并对这段折断下来的间距做特别处理，要“另眼相看”这段折断间距，折断、剔除的方式是插入一个来自物理实验的常数，插入的基本原则是让万有引力定律在两个质点m1、m2之间的距离趋于零的情况下，两个质点m1、m2之间的相互作用力f
12
不是无穷大。
[0031]
重正化处理修正后的万有引力定律、也就是奇点力学下的万有引力定律可表示如下：
[0032]
任意两个质点m1、m2由通过连心线方向上的力f
12
相互吸引，该引力f
12
大小与它们质量的乘积m1m2成正比，与它们之间距离r加上场源最小常数rm的平方成反比，与两物体的化学组成和其间介质种类无关，两个质点m1、m2的体积都不能为零，其大小可以用场源最小常数rm来定义，即：
[0033][0034]
式中rm是奇点力学下的万有引力定律中的场源最小常数，场源最小常数rm的物理单位是长度单位“米”。
[0035]
奇点力学下的万有引力定律追求的是一个更加符合实验结果的数学表达式，其通过将从原点出来的一段尺寸“作废”的形式，来避开两个质点m1、m2之间的相互作用力f
12
会出现无穷大的不合理结果，从而让奇点力学下的万有引力定律可以用于分析、处理两个质点m1、m2处于“重合”状态时相互之间的万有引力的大小，换言之，奇点力学下的万有引力定律其实并没有改动现有的万有引力定律，只是对其的应用范围做了一个新的限定和划分，即在场源最小常数rm之内，不能再利用万有引力定律计算两个质点m1、m2之间的万有引力f
12
的大小。实际上，两个质点m1、m2之间的万有引力f
12
在场源最小常数rm的边界处即达到了最大值，这个量值已经不能更大了，这意味着，如果两个质点m1、m2的中心点之间的距离小于场源最小常数rm，两个质点m1、m2之间的万有引力f
12
的大小也不会继续增大。
[0036]
在质点m1或m2的场源最小常数rm的内部，质点m1或m2的万有引力f
12
在方向上会反向，或者是在质点m1或m2的场源最小常数rm的内部是没有万有引力f
12
，从而让两个质点m1或m2分别保留一个自己的体积空间，不会塌缩成一个没有体积的数学点。
[0037]
上述奇点力学下的万有引力定律中的场源最小常数的物理含义是：两个体积不能为零的质点，在两个质点m1、m2之间相距为零的情况下、呈现出来的一个由引力场作用带来的空间常数，在场源最小常数rm的空间范围内，两个质点m1、m2之间即使有相对运动，也应该
视为两个质点m1、m2相距为零，即两个质点m1、m2是处于没有空间间隔的位置叠加态。请注意，这个位置叠加态是引力场下的位置叠加态，其量值会不同于电磁场下的位置叠加态。
[0038]
与之对应的，一个质量为m的质点在奇点力学下引力场的场强em为：
[0039][0040]
在r＝0处，这一关系式表明质点的引力场场强的最大值处即为质量为m的质点所在位置。
[0041]
一个质量为m的质点的奇点力学下引力场的势函数um为：
[0042][0043]
对于一个静止的质量为m的质点，在r＝0处，可以得到如下关系：
[0044][0045]
由于奇点力学下的两个质点的体积都不能为零，故任意两个质点m1、m2之间的距离在奇点力学下就是r+rm，不再是现有知识中的r；也就是说，即使是r＝0，在引力场中，任意两个质点之间也还是有一个rm的常数距离，这是由于两个质点m1、m2处于位置叠加态的结果。
[0046]
基于位置叠加态而产生的场源最小常数rm不同于常规的距离，如果用坐标系来描述的话，由于来自物理实验的场源最小常数rm不是一个数学点，而是一段不可拆开进行数学处理的空间长度，故带有场源最小常数rm的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数rm从公式中撤下来，等到推到完成数学推导后再将场源最小常数rm重新插入公式中。
[0047]
如果考虑广义相对论对牛顿引力的修正，对于一个质量为m的中心天体造成的时空弯曲，边上有一个小质量m物体运动，并假设如下：
[0048]
1、中心天体的质量m不太大，产生的时空弯曲比较小，比如中心天体为普通的恒星或行星；
[0049]
2、中心天体的质量m远大于小物体的质量m。
[0050]
那么，可以得到小物体在奇点力学下考虑了广义相对论对牛顿引力修正的等效势能v(r)为：
[0051][0052]
其中l是小质量物体的角动量，这里的负号代表吸引作用。
[0053]
与上述奇点力学下的等效势能对应的奇点力学下的等效引力f为：
[0054][0055]
对于核子之间的强相互作用，汤川秀树提出了核力势(yukawa)的表达式：
[0056][0057]
其中α为一个系数，m为介子的质量。
[0058]
下面我们直接给出奇点力学下的汤川势(yukawa)的表达式：
[0059][0060]
式中的rh为奇点力学下的核力场的场源最小常数，场源最小常数rh的物理单位是长度单位“米”。
[0061]
奇点力学下的汤川核力势的表达式是一个更加符合实验结果的数学表达式，其通过将从核子“原点”出来的一段尺寸“作废”的形式，来避开核子的核力势会出现无穷大的不合理结果，从而让奇点力学下的汤川核力势可以用于分析、处理两个核子处于“重合”状态时相互之间的核力的大小，换言之，奇点力学下的汤川核力势其实并没有改动现有的汤川核力势，只是对其的应用范围做了一个新的限定和划分，即在场源最小常数rh之内，不能再利用汤川核力势计算其大小。实际上，两个核子之间的相互作用在场源最小常数rm的边界处即达到了最大值，这个量值已经不能更大了，这意味着，如果两个核子的中心点之间的距离小于场源最小常数rh，两个核子之间的相互作用的大小也不会继续增大。
[0062]
在核子的场源最小常数rh的内部，核力的相互作用在方向上会反向，或者是在核子的场源最小常数rm的内部是没有核力的，从而让核子分别保留一个自己的体积空间，不会塌缩成一个没有体积的数学点。
[0063]
实验表明，核力是短程力，作用范围在1.5*10-15
米之内。核力在大于0.8*10-15
米时表现为吸引力，且随距离增大而减小，超过1.5*10-15
米时，核力急速下降几乎消失；而在距离小于0.8*10-15
米时，核力表现为斥力，因此，核力势的场源最小常数rm＝0.8*10-15
米。
[0064]
直观的看，奇点力学下的汤川势中的场源最小常数rh的场源的几何图形是一个球面，这就带来了下面的一系列的问题：
[0065]
1、首先，我们可以确定在场源最小常数rh范围的外面，也就是在场源球面之外，距离越接近核子，汤川势会越大，到了场源球面上，也就是核子在场源最小常数rh处，会出现汤川势的最大值，也就是具有最稳定的物理状态。
[0066]
2、当两个核子相互继续重合、以至于进入场源最小常数rm的“场源内部”范围后，则由于脱离了最稳定的物理状态，故其需要具有克服这一势能的动能才能实现。
[0067]
4、本发明的奇点力学下的汤川势的数学公式无法给出一个核子在另一个核子的场源最小常数rh内部所受的核力的大小，因为我们的实验数据代入的物理模型不能处理这种情况。
[0068]
5、从粒子相互碰撞实验结果看，一个更加合理的假设是这样的核力相互作用有可能不存在，即一个核子在另一个核子的场源最小常数rh的场源内部应该是自由的、不受核力作用的。
[0069]
我们无法排除一个核子的场源最小常数rm的场源内部具有与场源最小常数rh外面的核子方向相反的场强。但由于我们无法进入一个核子的场源最小常数rh的场源内部进行物理实验，所以对此只能是依赖猜想进行处理。
[0070]
6、假设核子的波动方程满足：
[0071]
ψ(r+rh，t)＝ψ0exp{ik(r+rh)-iωt}
[0072]
上式中的虚数坐标，就体现的是核子的场源内的位置函数，也就是“粒子”在场源的几何空间内的位置函数。当r＝0时，体现的就是核子在场源最小常数rh范围内的位置函
数。
[0073]
7、本发明人更愿意认为场源最小常数rh代表的是真实核子的一个重要的物理特性。所谓的核子的位置极限其实就是该核子的场强最大值所在的位置，场就是粒子，粒子可以用场源场强来描述其大小和位置，除此之外，没有其他的物理量可以用来描述粒子的位置和大小。
[0074]
核子的场源的数学点坐标可以同时处于其场源最小常数rh内的不同地方。如果你真的测量其中一个数学点的准确位置，那你测量到的就是其场源最小常数rh内的其中一个具体位置，至于具体是哪个数学坐标点，完全是随机的，这个频率的分布是概率分布，也就是波函数。
[0075]
基于引力场中两个质点m1、m2之间的数学距离不能小于场源最小常数rm，我们给出奇点力学下的引力场中，一个建立在物理的质点上的右手笛卡尔直角坐标与球坐标的变换和反变换公式：
[0076][0077][0078]
z＝r cosθ＝(r+rm)cosθ
[0079]
式中的r＝r+rm就是奇点力学下用一个物理的、有体积的质点作为坐标原点与坐标系中其他坐标点之间的距离；请注意，此处奇点力学下的万有引力定律中的场源最小常数的rm是利用实验数据直接插入的，场源最小常数rm可以用于描述位置叠加态下两个质点m1、m2之间的坐标变换关系。
[0080]
请注意，基于物理实验得到的场源最小常数rm不同于常规的距离，如果用坐标系的坐标点来描述位置关系的话，由于场源最小常数rm不是一个数学点，而是一段不可拆开进行数学处理的空间长度，故带有场源最小常数rm的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数rm从公式中撤下来，等到推到完成数学推导后再将场源最小常数rm重新插入公式中。
[0081]
当r＝0时，也就是二个粒子之间的距离为零时，引力场中奇点力学下，一个建立在物理的质点上的的右手笛卡尔直角坐标与球坐标的变换和反变换公式为：
[0082][0083][0084]
z＝r cosθ＝rmcosθ
[0085]
在奇点力学下的引力场中，如果一个具有体积的质点的空间坐标q1、q2、q3随时间的变化是由一个单值定律来表示的，那么，这个质点的运动就完全确定了，于是：
[0086]
q1＝q1(t)+rm；q2＝q2(t)+rm；q3＝q3(t)+rm；
[0087]
这些方程与单矢量方程
[0088]
r＝r(t)+rm[0089]
等价。式中r是连接坐标原点和运动质点m(q1+q2+q3)的矢径。如果质点m(q1+q2+q3)的直角坐标等于x，y，z，那么
[0090]
r＝r(t)+rm＝xi+yj+zk
[0091]
式中i，j、k是和坐标轴ox，oy，oz的正方向一致的单位矢量，而矢量xi，yj，zk是矢径r＝r(t)+xm沿0x，oy，oz坐标轴的分量。
[0092]
在奇点力学中，运动质点的矢径r＝r(t)+rm和坐标q1、q2、q3对时间的导数可表示为：
[0093][0094][0095]
基于引力场中两个质点m1、m2之间外在距离不能小于场源最小常数rm，下面我们直接给出在奇点力学下的引力场中，静止坐标系的原点和运动坐标系的原点都是建立在体积不为零的质点上的伽利略坐标变换：
[0096]
x-x
′
＝rm+vt
[0097]
y-y
′
＝rm[0098]
z-z
′
＝rm[0099]
t-t
′
＝tm＝rm/v
[0100]
基于引力场中两个质点m1、m2之间的数学距离不能小于场源最小常数rm，下面我们直接给出在奇点力学下的引力场中、静止坐标系的原点和运动坐标系的原点都是建立在体积不为零的质点上的洛伦兹坐标变换：
[0101][0102]
y-y
′
＝rm[0103]
z-z
′
＝rm[0104][0105]
再次强调，基于位置叠加态而产生的场源最小常数rm不同于常规的距离，如果用坐标系的坐标点来描述位置关系的话，由于场源最小常数rm不是一个数学点，而是一段不可拆开进行数学处理的空间长度，故带有场源最小常数rm的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数rm从公式中撤下来，等到推到完成数学推导后再将场源最小常数rm重新插入公式中。
[0106]
基于引力场中两个质点m1、m2之间的数学距离不能小于场源最小常数rm，我们定义在奇点力学下，如果质点m1、m2是在引力场作用下改变运动状态，则该粒子的运动距离可以采用两个质点m1、m2之间的奇点距离r＝r+rm，由此我们得出在奇点力学下两个质点m1、m2之间的奇点速度概念，即：
[0107]
1、奇点平均速度：在δt时间内，如果两个质点m1、m2之间的非位置叠加态位移为δr，则其奇点位移为r＝δr+rm，那么，奇点位移与时刻δt的比值，即为该质点在在δt时间内的奇点平均速度v为：
[0108][0109]
请注意，在δt时间内，当两个质点m1、m2之间的距离δr为零时，两个质点m1、m2之间还可以存在一个叠加态位移运动，也就是两个质点m1、m2处于位置叠加态下的运动，在这个叠加态位移下的奇点平均速度v为：
[0110][0111]
在这种情况下，两个质点m1、m2之间的奇点平均速度v就是一种奇点的内在运动。我们也可以这么看，当两个质点m1、m2之间的位移δr为零时，两个质点m1、m2实际上是合并为一个质点，而一个质点的二个部分之间可以存在一种内在的运动，也就是处于位置叠加态下的运动，这个运动会趋于让两个质点m1、m2相互分离开，两个质点分离所需要的时间间隔δtm是：
[0112][0113]
2、奇点瞬时速度v：在dt时间内，如果两个质点m1、m2之间的非位置叠加态位移为dr，则其奇点位移为r＝δr+rm，那么，奇点位移与时刻dt的比值，即为该点电荷在在dt时间内的奇点瞬时速度v为：
[0114][0115]
作圆周运动两个质点m1、m2之间的奇点瞬时速度v：
[0116][0117]
上面的ω为质点在奇点力学下的旋转运动。
[0118]
请注意，在dt时间内，当两个质点m1、m2之间的非位置叠加态旋转位移为零时，奇点力学下作圆周运动的奇点瞬时速度v为：
[0119][0120]
在这种情况下，两个质点m1、m2之间的奇点瞬时速度v就是一种奇点的叠加态自旋运动。
[0121]
假设内在运动的奇点瞬时速度v为光速c，则又可以得到一个新的常量——奇点力学下的零时间常数dt＝rm/c。
[0122]
在光速下，我们有c＝rmω。
[0123]
3、奇点瞬时加速度a：
[0124][0125]
4、对于圆周运动，奇点处的向心加速度a：
[0126][0127]
当r＝0时，
[0128][0129]
不难理解，如果没有了作为引力源的rm，向心加速度a也将成为“无源之水”，无法继续存在。
[0130]
5、奇点力学下的牛顿第二运动定律：
[0131][0132]
6、奇点力学下的圆周长l的计算公式：
[0133]
l＝2πr＝2π(r+rm)
[0134]
当r＝0时，
[0135]
l＝2πr＝2πrm[0136]
7、奇点力学下的圆面积s的计算公式：
[0137]
s＝πr2＝π(r+rm)2[0138]
当r＝0时，
[0139]
s＝πr2＝πr
m2
[0140]
8、奇点力学下的圆球体积v的计算公式：
[0141][0142]
当r＝0时，
[0143][0144]
当r＝0时，对于一个质量为m的质点，该质点的质量密度ρ为：
[0145][0146]
9、奇点力学下的做功的计算公式：
[0147][0148]
如果则
[0149][0150]
一个质量为m的质点的奇点力学下引力场的势函数u为：
[0151][0152]
库仑定律(coulomb’s law)是静止点电荷相互作用力的规律，1785年法国科学家c，-a.de库仑由实验得出，库仑定律的常见表述：
[0153]
真空中两个静止的点电荷之间的相互作用力，与它们的电荷量的乘积(q1q2)成正比，与它们的距离(数学距离)的二次方(r2)成反比，作用力的方向在它们的连线上，同性电荷相斥，异性电荷相吸。即：
[0154][0155]
与万有引力定律类似，现有的库伦定律也存在一个明显的缺陷，就是在两个点电荷q1、q2之间的距离趋于零的情况下，电场力f
12
会趋于无穷大，但是，这明显与事实不符，也就是说，在两个点电荷q1、q2之间相距为零时，两个点电荷q1、q2之间的相互作用力f
12
也不可能是无穷大。事实上，即使两个点电荷q1、q2之间的距离趋于零，电场力f
12
也只能是趋于一个常数，绝不会是无穷大。
[0156]
现有的物理实验可以定性地证明，当二个点电荷q1、q2重合时，并没有释放出无穷大的能量，例如，正负电子对的湮灭反应，即是例证。
[0157]
基于上述要求，可对现有的库伦定律进行重正化的方案，是重新审视现有的库伦定律的分母项中的距离r项，将距离r段中位于中心点处的一段距离从利用库伦定律的数学计算中剔除掉，也就是从原点开始、在向外的方向上的间距折断下来一段长度，并对这段折断下来的间距做特别处理，要“另眼相看”这段折断间距，折断、剔除的方式是插入一个来自物理实验的常数，插入的基本原则是让库伦定律在两个点电荷q1、q2之间的距离趋于零的情况下，两个点电荷q1、q2之间的相互作用力f
12
不是无穷大。毋庸置疑，这一修正要最大限度地包容现有的库伦定律符合的平方反比定律这一实验事实，而不能违反这一实验结果。
[0158]
重正化处理修正后的库伦定律、也就是奇点力学下的库伦定律可表示如下：
[0159]
任意两个点电荷q1、q2由通过连心线方向上的力f
12
相互吸引，该电场力f
12
大小与它们电量的乘积q1q2成正比，与它们之间距离r(非叠加态下的距离)加上场源最小常数re的平方成反比，两个点电荷q1、q2的体积都不能为零，其大小可以用场源最小常数re来定义，即：
[0160][0161]
式中re是奇点力学下的库伦定律的场源最小常数，场源最小常数的物理单位是长度单位“米”。
[0162]
奇点力学下的库伦定律追求的是一个更加符合实验结果的数学表达式，其通过将从原点出来的一段尺寸“作废”的形式，来避开两个点电荷q1、q2之间的相互作用力f
12
会出现无穷大的不合理结果，从而让奇点力学下的库伦定律可以用于分析、处理两个点电荷q1、q2处于“重合”状态时相互之间的库伦作用的大小，换言之，奇点力学下的库伦定律其实并没有改动现有的库伦定律，只是对其的应用范围做了一个新的限定和划分，即在场源最小常数re之内，不能再利用库伦定律计算两个点电荷q1、q2之间的库伦作用f
12
的大小。实际上，两个点电荷q1、q2之间的库伦作用f
12
在场源最小常数re的边界处即达到了最大值，这个量值已经不能更大了，这意味着，如果两个点电荷q1、q2的中心点之间的距离小于场源最小常数re，两个点电荷q1、q2之间的库伦作用f
12
的大小也不会继续增大。
[0163]
在点电荷q1、q2的场源最小常数re的内部，质点m1或m2的库伦作用f
12
在方向上会反向，或者是在点电荷q1、q2的场源最小常数re的内部是没有库伦作用f
12
，从而让两个点电荷q1、q2保留一个自己的体积空间，不会塌缩成一个没有体积的数学点。
[0164]
奇点力学下的库伦定律追求的是一个更加符合实验结果的数学表达式，显而易见的，奇点力学下的库伦定律可以用于分析、处理两个点电荷q1、q2处于重合状态时相互之间
的万有引力的大小，但由于数学工具的高度理想化特点与物理实验的数据必然会有测量误差的事实，显然，我们不可能完全验证这个数学公式是否严格成立，我们追求的目标只是近似成立，只是“能用”即可。
[0165]
奇点力学下的库伦定律中的场源最小常数re的物理含义是：体积不能为零的两个点电荷q1、q2，在两个点电荷q1、q2相距为零的情况下呈现出来的一个由静电场作用带来的空间常数，在场源最小常数re的范围内，两个点电荷q1、q2之间即使有相对运动，也应该视为两个点电荷q1、q2相距为零，即两个点电荷q1、q2是处于没有空间间隔的位置叠加态。
[0166]
在此需要强调的是，任意两个点电荷q1、q2之间有一个在奇点力学下的奇点距离r，在奇点力学下任意两个点电荷q1、q2之间的奇点距离r就是r+re，不再是现有知识中的非叠加态距离r。也就是说，即使是非叠加态距离r＝0，任意两个点电荷q1、q2之间也还是有一个re的位置叠加态的常数距离。即：对于奇点力学而言，任意两个点电荷q1、q2之间的奇点距离r＝r+re。
[0167]
与之对应的，一个电量为q1的点电荷在奇点力学下电场的场强ee为：
[0168][0169]
在r＝0处，
[0170][0171]
这一关系式表明点电荷q1的电场强度的最大值处即为点电荷q1所在位置。
[0172]
一个电量为q1的点电荷的奇点力学下电场的电势ue为：
[0173][0174]
直观的看，奇点力学下的库伦定律中的场源最小常数re的几何图形是一个球面，这就带来了下面的一系列的问题：
[0175]
1、首先，我们可以确定在场源最小常数re范围的外面，也就是在场源球面之外，两个点电荷q1、q2之间相距越小，库伦力会越大，到了球面之上，也就是两个点电荷q1、q2相互贴合在场源最小常数re处，会出现两个点电荷q1、q2之间的库伦力的最大值。
[0176]
2、其次，由于两个点电荷q1、q2贴合在场源最小常数re处会出现库伦力的最大值的结果，故两个点电荷q1、q2之间在在场源球面上，也即相距re处具有最小势能，也就是此处具有最稳定的物理状态。
[0177]
3、当两个点电荷q1、q2相互继续重合、以至于进入场源最小常数re的“场源球面内部”范围后，则由于脱离了最小势能状态，故其需要具有克服这一势能的动能才能实现。
[0178]
4、本发明的奇点力学下的库伦定律的数学公式无法给出一个点电荷q1在另一个点电荷q2的场源最小常数re的场源内部所受的库伦力(假如还能称之为库伦力的话)的大小，因为我们的实验数据代入的物理模型不能处理这种情况。
[0179]
5、从粒子相互碰撞实验结果看，一个更加合理的假设是这样的库伦力相互作用有可能不存在，即一个点电荷q1在另一个点电荷q2的场源最小常数re的场源内部应该是自由的、不受万有引力作用的，因为在场源最小常数re的场源内部电场强度应该是零。
[0180]
我们无法排除一个点电荷q1的场源最小常数re的场源内部具有与场源最小常数re外面的电场方向相反的场强。但由于我们无法进入一个点电荷q1的场源最小常数re的场源内部进行物理实验，所以对此只能是以猜想进行处理。
[0181]
6、由于我们已经认定两个点电荷q1、q2之间外在距离就是r+re，如果两个点电荷q1、q2是没有体积大小的数学点，则两个点电荷q1、q2之间外在数学距离不能小于场源最小常数re，因为这会让电场的场强大于实验得到的物理场强。
[0182]
而在场源最小常数re的场源内部，我们只能认为两个点电荷q1、q2之间的距离是真实的、物理的负空间尺度，在我们这个“正”物理空间中所有的观察者看来，在这种状态下的两个点电荷q1、q2无论怎样运动，这二个粒子之间都不会产生任何的物理间距。两个点电荷q1、q2之间的“场源内在距离”和“场源内在速度”在量子力学中会有更直观的物理意义。
[0183]
假设点电荷q1的波动方程满足：
[0184]
ψ(r+re，t)＝ψ0exp{ik(r+re)-iωt}
[0185]
上式中的虚数坐标，就体现的是点电荷q1的场源内的位置函数，也就是“粒子”在场源的几何空间内的位置函数。当r＝0时，体现的就是点电荷q1在场源最小常数re范围内的位置函数。
[0186]
7、本发明人更愿意认为场源最小常数re代表的是真实电场的一个重要的物理特性。所谓的粒子的位置极限其实就是该粒子的场强最大值所在的位置，场就是粒子，粒子可以用场强来描述其大小和位置，除此之外，没有其他的物理量可以用来描述粒子的位置和大小。
[0187]
那么，我们该如何理解电场性质的“粒子”的位置呢？奇点力学的解释是：电场性质的“粒子”、也就是电场的“场源”以及场源外面的“扩展源”部分可以同时具有不同数学点下的位置的状态，这个状态叫叠加态。换言之，场源最小常数re本身就可以让其同时具有不同(数学点下)的位置的状态，当你非要用测量寻找其中的一个数学点来定义力场性质的“粒子”的位置时，这样的测量会让你随机地获得其中的一个状态，并且当你测量它的时候，这个处在叠加态的系统的波函数就随机地坍塌缩成其中的一个波函数。
[0188]
比如，电子的电场的场源的数学点坐标可以同时处于其场源最小常数re内的不同地方。如果你真的测量其中一个数学点的准确位置，那你测量到的就是其场源最小常数rm内的其中一个具体位置，至于具体是哪个数学坐标点，完全是随机的。
[0189]
你准备100个完全相同的测试物，并测量它们的状态，你会得到100个结果。但可能某些结果出现的频率高些，某些结果出现的频率低些，出现的最高的应该是在场源最小常数re的场源内部的数学坐标点，位于场源最小常数re的场源外侧的数学坐标点出现的几率会低一些，这个频率的分布是概率分布，也就是波函数。
[0190]
那么，库伦定律中的场源最小常数re的物理意义是什么呢？奇点力学下的任意两个点电荷q1、q2之间的非数学的奇点距离r的物理意义又是什么呢？
[0191]
下面我们直接给出多个具体的应用答案。
[0192]
如上所述，我们定义在奇点力学下，如果点电荷q1、q2是在电场作用下改变运动状态，则该粒子的运动距离可以采用任意两个点电荷q1、q2之间的奇点距离r＝r+re，由此我们得出在奇点力学下的奇点速度概念，即：
[0193]
1、奇点平均速度：在δt时间内，如果两个点电荷q1、q2之间的非位置叠加态位移为δr，则其奇点位移为r＝δr+re(或者)那么，奇点位移与时刻δt的比值，即
为该点电荷在在δt时间内的奇点平均速度v为：
[0194][0195]
请注意，在δt时间内，当两个点电荷q1、q2之间的非位置叠加态位移为δr为零时，则两个点电荷q1、q2之间的位置处于叠加态，其叠加态位移平均速度v为：
[0196][0197]
在这种情况下，奇点平均速度v就是一种叠加态的内在运动。
[0198]
2、奇点瞬时速度：在dt时间内，如果两个点电荷q1、q2之间的非位置叠加态位移为dr，则其奇点位移为r＝δr+re(或者)，那么，对于圆周运动，奇点位移与时刻dt的比值，即为该点电荷在在dt时间内的奇点瞬时速度v为：
[0199][0200]
请注意，当两个点电荷q1、q2之间的非位置叠加态位移为δr为零时，则两个点电荷q1、q2之间的位置处于叠加态，则其叠加态位移瞬时速度v为：
[0201][0202]
在这种情况下，奇点瞬时速度v和自旋角速度ω就是一种奇点的内在运动。
[0203]
3、奇点瞬时加速度a：
[0204][0205]
4、对于圆周运动，奇点处的向心加速度a：
[0206][0207]
当r＝0时，
[0208][0209]
不难理解，如果没有了作为向心力来源的re，向心加速度a也将无法继续存在。
[0210]
5、奇点力学下的牛顿第二运动定律：
[0211][0212]
6、奇点力学下的圆周长l的计算公式：
[0213]
l＝2πr＝2π(r+re)
[0214]
当r＝0时，
[0215]
l＝2πr＝2πre[0216]
7、奇点力学下的圆面积s的计算公式：
[0217]
s＝πr2＝π(r+re)2[0218]
当r＝0时，
[0219]
s＝πr2＝πr
e2
[0220]
8、奇点力学下的圆体积d的计算公式：
[0221][0222]
当r＝0时，
[0223][0224]
9、奇点力学下的做功的计算公式：
[0225][0226]
如果则
[0227][0228]
10、平行板电容器的真空电容c：
[0229][0230]
式中d为两极板内表面之间的距离。
[0231]
在奇点力学下，一个在有心力场中运动的物体的euler-lagrangian方程可以表示为：
[0232][0233]
上式中的r0为有心力场的场源最小常数。
[0234]
利用euler-lagrangian方程，可以得到
[0235][0236]
即角动量是一个守恒量。
[0237]
下面我们直接给出奇点力学下关于euler-lagrangian的运动方程：
[0238][0239]
下面利用高斯定理来推导奇点力学下的库伦定律。
[0240]
高斯定理(gauss’law)也称为高斯通量理论(gauss’flux theorem)，或称作散度定理、高斯散度定理、高斯-奥斯特罗格拉德斯基公式、奥氏定理或高-奥公式。
[0241]
在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。高斯定律(gauss’law)表明在闭合曲面内的电荷分布与产生的电场之间的关系。高斯定律在静电场情况下类比于应用在磁场学的安培定律，而二者都被集中在麦克斯韦方程组中。因为数学上的相似性，高斯定律也可以应用于其它由平方反比律决定的物理量，例如引力或者辐照度。
[0242]
奇点力学下的高斯定理指出：穿过一封闭曲面的电通量与奇点力学下的封闭曲面所包围的电荷量成正比，换一种说法：电场强度在一封闭曲面上的面积分与奇点力学下的封闭曲面所包围的电荷量成正比，即：
[0243][0244]
我们定义点电荷q1、q2
…
qi
…
的体积都不能为零，在这种情况下，奇点力学下的高斯定理推导出来的一个点电荷电场的公式：
[0245][0246][0247]
奇点力学下该点电荷的电势u为：
[0248][0249]
上式中电场强度e的物理意义是：当我们用测试电荷测试电场强度时，即使测试电荷与粒子之间的距离r＝0，被测试的点电荷还是存在的，并且这个点电荷还是可以位于一个球面内，在实际中该点电荷体积是非常小，但不能为零，该点电荷的半径是re，该点电荷的表面积是4πr
e2
，被4πr
e2
包围在其中的点电荷的电量是q，表面积是4πr
e2
球面上的电通量依然是有限的常量，不能是无穷大。所以，我们用r+re作为积分计算的上限边界，用零作为积分计算的下限边界。也就是说，点电荷与测试电荷之间的距离在奇点力学下就是r+re，不再是现有知识中的r，即使是r＝0，点电荷与测试电荷之间也还是有一个re的常数距离。
[0250]
上述关于高斯定理的分析计算同样适用于万有引力定律的引力场。
[0251]
在静磁学中，毕奥-萨伐尔定律(英文：biot-savart law)描述电流元在空间任意点p处所激发的磁场。毕奥-萨伐尔定律表示如下：
[0252]
电流元idl在空间某点p处产生的磁感应强度db的大小与电流元idl的大小成正比，与电流元idl所在处到p点的位置矢量和电流元idl之间的夹角的正弦成正比，而与电流元idl到p点的距离r的平方成反比。
[0253][0254]
μ0为真空磁导率；
[0255]
现有的毕奥-萨伐尔定律存在一个明显的缺陷，就是在电流元idl到p点之间的距离趋于零的情况下，磁感应强度db会趋于无穷大，但是，这个结论显然与事实不符，因为p点即使是在电流元idl的原点处，也不可能产生无穷大的磁感应强度db。事实上，即使电流元idl到p点之间之间的距离趋于零，磁感应强度db也只能是趋于一个常数，绝不会是无穷大，换言之，即使在构成电子流的一个个电子所在的原点处，该处的磁感应强度db也只能是一个常数，绝不会是无穷大。因此，需要从实验出发，对现有的毕奥-萨伐尔定律进行重正化处理，让其避免磁感应强度db会出现无穷大的结论，修正后的毕奥-萨伐尔定律可表示如下：
[0256]
电流元idl在空间某点p处产生的磁感应强度db的大小与电流元idl的大小成正比，与电流元idl所在处到p点的位置矢量和电流元idl之间的夹角的正弦成正比，而与电流元idl到p点的距离r加上距离修正常数rb的平方成反比，即：
[0257]
[0258]
式中rb是毕奥-萨伐尔定律的距离修正常数。
[0259]
需要说明的是，在得到足够精确、足够多的实验数据后，通过插入实验数据进行计算，有可能发现距离修正常数rb不是一个常数，而是变化不定的变数，这表明修正后的二个毕奥-萨伐尔定律的公式都不对，这时候就要根据这一具体情况调继续整毕奥-萨伐尔定律的表达式，直至根据实验数据计算出来的距离修正常数rb非常贴近于一个常数为止，这时候的磁场强度的表达式才是最符合实际状态的、也更加精确的磁场强度计算公式。
[0260]
需要指出的是，毕奥-萨伐尔定律的距离修正常数rb的具体数值是多少，人们在目前并不知道。因此，有必要通过实验测量来得到毕奥-萨伐尔定律中距离修正常数rb的具体数值。
[0261]
下面我们直接给出奇点力学下的麦克斯韦方程组：
[0262]
(奇点力学下的安培环路定律)
[0263]
(奇点力学下的法拉第电磁感应定律)
[0264]
(奇点力学下的电场的高斯定律)
[0265]
(奇点力学下的磁场的高斯定律)
[0266]
式中的re为电场的场源最小常数，rb为磁场的场源最小常数，其具体的数值需要从实验中得出。请注意，作为场源的re和rb，是可以脱离电荷而独立存在的，即以光速运动的光子也可以有自己的rm、re和rb。
[0267]
而电磁场的波动运动，也是围绕着电场的场源最小常数re和磁场的场源最小常数rb的球形边界进行的，电场的波动运动和磁场的波动运动都体现为收缩到电场的场源最小常数re的球形边界的内部和磁场的场源最小常数rb的球形边界的内部来对外界表达波动性。
[0268]
根据电流的定义，可知j＝ρv，据此可得：
[0269][0270]
波区是指离开辐射源的距离大大超过辐射系统的线度和它的辐射波长的空间范围。在波区的某个局部小区域内，可以将电磁波视为平面波，在波区内，辐射系统的电磁辐射可以用推迟矢势a来确定。
[0271]
如果坐标原点选择在辐射系统的有限范围内，即与辐射波长相比是很小的，那么，在波区内，奇点力学下的场的推迟矢势a为：
[0272][0273]
式中r+re＝至场的被观察点的矢径；r+re＝|r+re|；
[0274]r′
+re＝至场的辐射系统体积元dy
′
的矢径；
[0275]
为了便于理解库伦定律中场源最小常数，我们回顾一下声学基础理论中相关的知识。众所周知，在声学基础理论中，如果势函数以及其他表征介质波动介质波动特性的物理量仅与时间以及空间上称为波心的某一点的距离r有关，这样的纵波称为纵球面波。在各项同性均匀介质中，由点源激起的波就是球面波。所谓点源指的是其线度可以被视为非常
小的点状振动体。
[0276]
在奇点力学中，我们用奇点距离r＝r+r0代替r，故纵球面波的波动方程是：
[0277][0278]
当距离r＝0时，在奇点力学中纵球面波的波动方程变为：
[0279][0280]
在奇点力学中，式(a)的纵球面波的波动方程的通解形式是：
[0281][0282]
这里的c是纵球面波的波速，f1和f2是任意函数，是发散球面波的势函数，是向中心汇聚的球面波的势函数，r0是纵球面波的场源最小常数。
[0283]
当距离r＝0时，也就是在点源处，在奇点力学下的纵球面波的波动方程的通解形式是：
[0284][0285]
球面波的波面是一组同心的球面，奇点力学下的发散球面正弦波的方程是：
[0286][0287]
式中k为波矢，α为波源振动的初相位，r为距离波源的距离，a0为在距离r等于1处各个质点振动的振幅，r0是发散球面正弦波的场源最小常数，场源最小常数r0需要通过实验测量得出。
[0288]
在点源处，奇点力学下的发散球面正弦波的方程是：
[0289][0290]
奇点力学下的球面波方程的指数形式是：
[0291][0292]
式中a为复振幅，
[0293]
其中，势函数在包括r＝0处全部满足波动方程：
[0294]
在点源处，奇点力学下的球面波方程的指数形式是：
[0295][0296]
通过以上对声学基础理论中相关知识的介绍，有助于我们理解纵球面波的场源最小常数的物理意义，即纵球面波的场源最小常数r0对应的是在点源处的势函数的状态。显然，任何真实的点源处的势函数不可能是无穷大，这也间接地证明了在库仑定律中，两个点电荷q1、q2之间的距离为零的情况下，两个点电荷q1、q2之间的电场力f
12
不可能是无穷大，
需要进行重正化处理，以避免出现无穷大的不合理数值。
[0297]
下面我们直接给出奇点力学下静电场中的薛定谔方程的表达式：
[0298][0299]
式中的re为静电场的场源最小常数。
[0300]
在奇点力学中，电场性质的“粒子”就是电场的“场源”，也包括场源外面的“扩展电场源”部分，因此，在奇点力学中，“粒子”可以同时具有不同数学点下的位置的状态，这个状态叫叠加态。换言之，场源最小常数re本身就可以让其同时具有不同(数学点下)的位置的状态，当你用测量寻找其中的一个数学点来定义力场性质的“粒子”的位置时，这样的测量会让你随机地获得其中的一个状态，并且当你测量它的时候，这个处在叠加态的系统的波函数就随机地坍塌缩成场源最小常数re中的一个波函数。
[0301]
比如，电子的电场的场源的数学点坐标可以同时处于其场源最小常数re内的不同地方。如果你真的测量其中一个数学点的准确位置，那你测量到的就是其场源最小常数rm内的其中一个具体位置，至于具体是哪个数学坐标点，完全是随机的。测量会让某些结果出现的频率高些，某些结果出现的频率低些，出现的最高的应该是在场源最小常数re的场源内部的数学坐标点，位于场源最小常数re的场源外侧的数学坐标点出现的几率会低一些，这个频率的分布是概率分布，也就是波函数。
[0302]
请注意，基于实验得到的场源最小常数re不同于常规的距离，如果用坐标系的坐标点来描述薛定谔方程的话，由于场源最小常数re不是一个数学点，而是一段不可拆开进行数学处理的空间长度，故带有场源最小常数re的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数re从公式中撤下来，等完成数学推导后再将场源最小常数re重新插入公式中。
[0303]
下面直接给出奇点力学下一束自由电子的波函数：
[0304][0305]
这个波动具有真实的、物理的虚数成分，即位于场源内部的a部分就是真实的、物理的虚数成分。
[0306]
下面直接给出奇点力学下氢原子中的电子处于基态时的波函数：
[0307][0308]
下面我们直接给出奇点力学下的球极坐标系中的氢原子薛定谔方程的表达式：
[0309][0310]
上式中的re为库伦定律下的场源最小常数。
[0311]
上述奇点力学下的球极坐标系中的氢原子薛定谔方程的表达式同样有助于我们更深刻的理解场源最小常数的物理含义。通过求解奇点力学下的球极坐标系中的氢原子薛定谔方程，也能对库伦定律下的场源最小常数re的具体数值进行理论计算。
[0312]
需要说明的是，奇点力学下的薛定谔方程表达式中，在奇点力学中有一个特殊的解，那就是当r＝0的解。
[0313]
如果实验证明则上面所有的r＝r+re全部替换为
[0314]
下面我们直接给出奇点力学下磁场中的薛定谔方程的表达式：
[0315][0316]
式中的rb为磁场的场源最小常数。
[0317]
请注意，基于实验得到的场源最小常数rb不同于常规的距离，如果用坐标系的坐标点来描述薛定谔方程的话，由于场源最小常数rb不是一个数学点，而是一段不可拆开进行数学处理的长度，故带有场源最小常数rb的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数rb从公式中撤下来，等到完成数学推导后，再将场源最小常数rb重新插入公式中。
[0318]
下面我们直接给出奇点力学下引力场中的薛定谔方程的表达式：
[0319][0320]
式中的rm为引力场的场源最小常数。
[0321]
再次强调，基于实验得到的场源最小常数rm不同于常规的距离，如果用坐标系的坐标点来描述位置关系的话，由于场源最小常数rm不是一个数学点，而是一段不可拆开进行数学处理的空间长度，故带有场源最小常数rm的公式在利用坐标系进行变换的数学处理时，可能会遇到一些困难。可能的解决方案是进行数学推导前先将场源最小常数rm从公式中撤下来，等到推到完成数学推导后再将场源最小常数rm重新插入公式中。
[0322]
下面我们直接给出奇点力学下电场中的德布罗意关系式的表达式：
[0323][0324]
下面我们直接给出奇点力学下磁场中的德布罗意关系式的表达式：
[0325][0326]
下面我们直接给出奇点力学下引力场中的德布罗意关系式的表达式：
[0327][0328]
需要注意的是，质量为m的粒子在奇点力学下的动量与粒子所受到的作用的场性质有关，而奇点力学下反应粒子波动性的λ的内在含义是什么，一个合理的推断是一个粒子的波长λ应该与存在于场源内的、需要用虚数坐标表达的“负长度”尺寸有关联。
[0329]
下面我们直接给出奇点力学下电场中的海森堡的测不准关系式的表达式：
[0330]
[0331]
下面我们直接给出奇点力学下磁场中的海森堡的测不准关系式的表达式：
[0332][0333]
下面我们直接给出奇点力学下引力场中的海森堡的测不准关系式的表达式：
[0334][0335]
由于真实的粒子存在的前提是粒子的体积不能为零，故奇点力学下的海森堡的测不准关系式，其实不过是基于实验数据对真实的粒子的体积不能为零的问题做了符合实际的修正处理。也就是说，传统上的数学点没有体积，不占有实际的空间，而真实的粒子是有体积、占有实际的空间，因此，真实的粒子的位置如果非要用“精确”的数学点来测量定位的话，那你测量到的数据肯定是不唯一的，即这个粒子的位置可以用多个数学点坐标来定位，用这些坐标点来定位真实的有体积的粒子的位置都是正确的，这就构成了所谓的“测不准”，因为我们确实无法对真实的有体积的粒子只用唯一的一个数学点坐标来描述其位置，我们所确定的唯一位置不可能是唯一的。
[0336]
对于奇点力学下任意粒子的薛定谔方程
[0337][0338]
现在多数人都认为量子理论是包含在对这个方程的统计解释之中的。即薛定谔方程描述了粒子状态随时间变化情况，如果微观粒子在t＝0时刻的状态为已知，则原则上可以通过该方程求得任意时刻t的状态
[0339]
令
[0340][0341]
可得到奇点力学下的定态薛定谔方程
[0342][0343]
式中的r0为场作用的场源最小常数。
[0344]
下面我们直接给出奇点力学下的kohn-sham方程：
[0345][0346]
下面我们直接给出奇点力学下的自由粒子的dirac方程：
[0347][0348]
下面我们直接给出奇点力学下的时空坐标对称的dirac方程：
[0349][0350]
下面我们直接给出奇点力学下的自由粒子的dirac方程的正负能态解，令：
[0351][0352]
经推导后可得到奇点力学下的自由粒子dirac方程的平面波解序列：
[0353][0354]
其中α＝
±
1。
[0355]
而奇点力学下的dirac方程的通解为：
[0356][0357]
下面我们直接给出奇点力学下的克莱因-戈登方程
[0358][0359]
下面我们直接给出奇点力学下的施瓦西度规(schwarschild metric)的表达式：
[0360][0361]
而奇点力学下的施瓦西度规的解为：
[0362][0363]
上式中的rm为万有引力定律下的场源最小常数，g为万有引力常数，m为天体的质量。
[0364]
于是，奇点力学下的施瓦西解的黑洞视觉半径rs为：
[0365][0366]
上述奇点力学下的施瓦西解的黑洞视觉半径rs的数学表达式无疑有助于我们更深刻的理解场源最小常数的物理含义。
[0367]
从奇点力学下的施瓦西解的黑洞视觉半径rs的数学表达式可以看出，一个粒子的质量只有在2gm-c2rm≥0的情况下才能成为黑洞，即令其质量满足以下关系：
[0368][0369]
如果不满足这个条件，则rs的数值会是负值。
[0370]
以下是在奇点力学下的广义相对论的钟慢效应的数学表达式：
[0371][0372]
当r＝0时，在奇点力学下的广义相对论的钟慢效应的数学表达式为：
[0373]
[0374]
在奇点力学下的广义相对论的尺缩效应的数学表达式为：
[0375][0376]
也就是
[0377][0378]
当r＝0时，在奇点力学下的广义相对论的尺缩效应的数学表达式为：
[0379][0380]
如果实验证明则上面所有的r＝r+rm全部换为
[0381]
下面直接给出在引力场中奇点力学下的狭义相对论的尺缩效应的数学表达式：
[0382][0383]
其中的l0为静止参照系中的尺长，而场源最小常数xm是不变的常量。
[0384]
下面直接给出在引力场中奇点力学下的狭义相对论的钟慢效应的数学表达式：
[0385][0386]
其中的δt0为静止参照系中的时间间隔，rm/c为奇点力学下的零时间常数，g为万有引力常数，c为光速。
[0387]
下面直接给出在静电场中奇点力学下的狭义相对论的尺缩效应的数学表达式：
[0388][0389]
其中的l0为静止参照系中的尺长。
[0390]
在奇点力学中，当二个粒子之间的间距r＝0时，由于粒子自身还有一个场源最小常数r0的存在，也就是粒子还有一个可叠加的尺寸常数，我们可以用“想象”这个放大镜将粒子所在的位置放大至“无穷大”，这样就有了一个新的空间让我们来分析被放大的粒子了。在这个被“想象”放大产生新的空间中，我们可以建立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用虚数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是虚数性质的波函数，虚数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间完全不同，在虚数三维空间坐标系中，物质的形态会发生变化，就是说，实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在虚数三维空间坐标系中观察时，会变成没有静止质量、以光速运动的场物质，这个物质形态的变化是我们放大基本粒子所在点至无穷大带来的观察效应。
[0391]
那么，我们在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子在
哪里呢，当然是即在实数三维空间坐标系中，也在虚数三维空间坐标系中，奇点力学下的薛定谔方程表达式中的波函数ψ就是这样的一个函数。
[0392]
波函数ψ就是在实数三维空间坐标系中存在、同时也在虚数三维空间坐标系中存在的函数。
[0393]
在实数三维空间坐标系中的基本粒子的波函数ψ在实数三维空间坐标系中表达出的是粒子性，在实数三维空间坐标系中的基本粒子的波函数ψ在虚数三维空间坐标系中表达出的是波动性。
[0394]
如果我们是对虚数三维空间坐标系中的基本粒子进行放大至无穷大的空间变化处理，这样还会出现一个新的空间让我们来分析虚数三维空间坐标系中被放大的粒子。在这个被“想象”放大产生新的空间中，我们还是可以建立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用超虚数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是超虚数性质的波函数，超虚数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间更是完全不同，在超虚数三维空间坐标系中，物质的形态会继续发生变化。
[0395]
如上所述，在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在虚数三维空间坐标系中观察时，会变成没有静止质量、以光速运动的场物质，这个物质形态的变化是我们放大基本粒子所在点至无穷大带来的观察效应。
[0396]
而在虚数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在实数三维空间坐标系中观察时，会变成虚粒子，也就是根本观测不到。这个物质形态的变化是虚数三维空间坐标系的性质带来的观察效应。但是，在超虚数三维空间坐标系中去观察在虚数三维空间坐标系空间中具有静止质量的基本粒子，该基本粒子会变成没有静止质量、以光速运动的场物质，这个物质形态的变化同样是我们放大该基本粒子所在点至无穷大带来的观察效应。
[0397]
我们同样可以用“想象”缩小镜将我们所在的这个宇宙空间缩小至“无穷小”，这样同样会出现一个新的空间，假设我们进入这个新的三维空间，并在这个被“想象”缩小产生新的空间中立一个新的三维空间坐标系，这个三维空间坐标系的坐标轴可以用超实数来表示，与之对应的波函数ψ在这个新的三维空间坐标系也是超实数性质的波函数，超实数三维空间坐标系与我们人类熟悉的实数三维空间坐标系空间完全不同，在超实数三维空间坐标系中，物质的形态也会发生变化，就是说，实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子，在超实数三维空间坐标系中观察时，会类似虚粒子，也就是根本观测不到。这个物质形态的变化是超实数三维空间坐标系的性质带来的观察效应。而在超实数三维空间坐标系中去观察在实数三维空间坐标系空间中以光速运动的场物质时，会发现这些场物质是具有静止质量的基本粒子，这个物质形态的变化同样是我们缩小该我们宇宙至无穷小带来的观察效应。
[0398]
需要指出的是，超实数三维空间坐标系也可以通过“想象”缩小镜将其缩小至“无穷小”，随之而产生的则是超超实数三维空间坐标系，如此循环向上，可以有无限多个新的实数三维空间坐标系。而超虚数三维空间坐标系也可以通过“想象”放大镜将其内部的一个点放大至“无穷大”，随之而产生的则是超超虚数三维空间坐标系，如此循环向下，可以有无限多个新的虚数三维空间坐标系。而一个真实的在某一空间坐标系中的“粒子”，可以在所有的三维空间坐标系中都存在，只不过其存在的形态是变化的，在不同性质的三维空间坐
标系，该粒子具有不同性质的物质形态。
[0399]
那么，我们在实数三维空间坐标系空间中观察看到的具有静止质量的基本粒子在哪里呢，当然是即在超实数三维空间坐标系中，也在虚数三维空间坐标系中，奇点力学下的薛定谔方程表达式中的波函数ψ同样就是这样的一个函数。
[0400]
波函数ψ就是在超实数三维空间坐标系中存在、同时也在虚数三维空间坐标系中存在的函数。
[0401]
如果超实数三维空间坐标系中的基本粒子的波函数ψ在超实数三维空间坐标系中表达出的是粒子性，在超实数三维空间坐标系中的基本粒子的波函数ψ在实数三维空间坐标系中表达出的就是波动性。
[0402]
众所周知，为了描述一个物体的运动，通常是选择另一个物体作为参照物，为了方便地描述物体之间的相对运动规律，我们应尽可能的选择与被描述物体存在相互作用或相对运动的物体作为参照系。我们规定与被描述物体之间存在相互作用或相对运动的、被选作参考的物体为相对参照系，被选作参考的物体的运动状态可以是任意的。
[0403]
用相对参照系描述物体之间的相对运动时，可以得到如下规律：
[0404][0405]
式中m1和m2分别为相互作用的二个物体的质量，f
12
为相互作用的二个物体之间的相互作用力，a
12
为相互作用的二个物体之间相对运动所具有的的加速度，f1是质量为m1的物体所受的外力作用，f2是质量为m2的物体所受的外力作用。以上数学表达式所表达的运动规律我们称之为相对运动定律。
[0406]
下面我们用相对运动定律来分析一个黑洞与另一个物体相互作用的运动规律。
[0407]
设黑洞1的质量为m1，物体2的质量为m2，假设二者之间只有彼此的万有引力作用，忽略其他的外力作用，由奇点力学下的万有引力定律：
[0408][0409]
以及相对运动定律，可得到：
[0410][0411]
整理得到二者之间相对运动的加谏度为：
[0412][0413]
设物体2在距离黑洞原点的奇点距离r处，也就是距离黑洞r+rm处，物体2的重力势能
[0414]
物体2要想与黑洞1脱离，其相对运动速度v所具有的相对能量要大于重力势能取二者正好相等为临界值，可以得到：
[0415][0416]
将相关的已知数据代入上式，并解这个方程式，就可以得到物体2在距离黑洞原点
的奇点距离r+rm处的脱离速度v与距离黑洞原点的奇点距离r+rm之间在临界值下的关系了，这个关系能帮助我们定性地了解万有引力定律中的场源最小常数rm的物理意义。
[0417]
实验发现，电子具有自旋运动，根据奇点力学，电子具有的自旋运动可以用奇点力学下的周长计算公式加以计算分析，即电子具有的自旋运动是在r＝0状态下、电子自身的旋转运动，根据奇点力学下的面积计算公式，电子的自旋面积s为：
[0418][0419]
在奇点力学下，电子自旋的周长l为：
[0420][0421]
再设定电子是一个稳定的圆环形驻波，即电子在虚数三维空间坐标系是在做自旋的环绕运动，自旋的周长为其波长λ，于是，得到电子自旋的半径rb为：
[0422][0423]
而电子自旋的电流强度i＝-ve，由此，我们可以计算出电子自旋的磁矩μs：
[0424][0425]
在上面的计算中电子自旋的半径rb为：
[0426][0427]
有可能就是与毕奥-萨伐尔定律中场源最小常数相关的数值，可以作为分析本发明的实验数据时的参考。
[0428]
照度第一定律：在用点光源照明时，与光线垂直的物体表明上的照度e跟光源发光的强度i成正比，跟被照亮的面到光源的距离r的平方成反比。即：
[0429][0430]
与万有引力定律类似，现有的照度第一定律也存在一个明显的缺陷，就是在被照亮的面到光源的距离r趋于零的情况下，照度e会趋于无穷大，但是，这明显与事实不符，也就是说，在被照亮的面到光源的距离r相距为零时，照度e不可能是无穷大。事实上，即使被照亮的面到光源的距离r相距为零时，照度e也只能是趋于一个常数，绝不会是无穷大。因此，需要从实验出发，对现有照度第一定律进行重正化处理，让其避免照度e会出现无穷大的结论，为此，可在照度第一定律的分母项中插入一个常数，插入的基本原则是让照度第一定律在被照亮的面到光源的距离r趋于零的情况下，照度e不是无穷大即可，修正后的照度第一定律、也就是奇点力学下的照度第一定律可表示如下：
[0431]
在用点光源照明时，与光线垂直的物体表明上的照度e跟光源发光的强度i成正比，跟被照亮的面到光源的距离r加上场源最小常数ri的平方成反比。即：
[0432][0433]
式中ri是奇点力学下的照度第一定律的场源最小常数。
[0434]
兰纳-琼斯势(lennard-jones potential)，又称l-j势，6-12势，或12-6势，是用来模拟两个电中性的分子或原子间相互作用势能的一个比较简单的数学模型。最早由数学家
约翰
·
兰纳-琼斯于1924年提出。由于其解析形式简单而被广泛使用，特别是用来描述惰性气体分子间相互作用尤为精确。
[0435]
兰纳-琼斯势能以两体距离为唯一变量，包含两个参数，下面我们直接给出奇点力学下的兰纳-琼斯势能：
[0436][0437]
式中的r0为兰纳-琼斯势的场源最小常数，ε为势能阱的深度，σ是互相作用的势能正好为零时的两体距离。在实际应用中，ε、σ参数往往通过拟合已知实验数据或精确量子计算结果而确定。
[0438]
从物理意义上讲，第一项可认为是对应于两体在近距离时以互相排斥为主的作用，第二项对应两体在远距离以互相吸引(例如通过范德瓦耳斯力)为主的作用。
[0439]
奇点力学下的兰纳-琼斯势相应的两体作用力为：
[0440][0441]
本发明的基于实验数据重正化库伦定律的方法，其包括如下步骤：
[0442]
a、准备二个可带电量分别为q1和q2的物体；
[0443]
b、准备一个用于测量静电力常数的装置；
[0444]
c、让二个物体分别带上q1和q2的电量，不需要对其所带电量进行计量，利用所述的用于测量静电力常数的装置，测量二个物体之间的库伦力f1的大小，同时测量得到二个物体之间的距离为r1，然后再改变二个物体之间的距离为r2，并再次测量出改变了二个物体之间的距离为r2后物体之间的库仑力f2的大小；
[0445]
e、根据修正后的库伦定律的其中一个如下形式的公式
[0446][0447]
将二次测量结果代入上式，分别得到：
[0448]
f1＝k q1q2/(r1+re)2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(22)
[0449]
f2＝k q1q2/(r2+re)2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(23)
[0450]
简化式(22)、式(23)二个方程式，可得到：
[0451]
f1/f2＝(r2+re)2/(r1+re)2ꢀꢀꢀꢀ
(24)
[0452]
再将通过实验测量到的f1、f2和r1、r2代入(24)式，即可得出库伦定律中场源最小常数re的具体数值。
[0453]
作为本发明的进一步改进，上述用于测量静电力常数的装置为卡文迪许扭秤，所述的二个物体分别为采用金属制成的空心球形体。