一种铣削系统稳定性状态获取方法与流程

本发明涉及数控加工中数字化制造领域，尤其是涉及一种铣削系统稳定性状态获取方法。

背景技术：

颤振是金属切削过程中的一种有害现象，当铣削过程发生颤振时，不稳定的工艺系统会加剧刀具的磨损、加速机床及夹具的破坏、降低加工效率以及产生大的噪声污染等。当铣削过程发生颤振时，铣削过程属于不稳定性的状态，探索铣削加工动力学模型，研究铣削动力学模型的稳定性，确定出稳定性的铣削参数用于指导实际加工。然而，从数学角度讲，铣削动力学模型属于具有时滞项的微分方程，该方程具有无限维的状态空间，使得对时滞微分方程进行稳定性分析时非常的困难，尚未有一种快速有效的铣削系统稳定性状态获取方法。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种铣削系统稳定性状态获取方法。

本发明的目的可以通过以下技术方案来实现：

一种铣削系统稳定性状态获取方法，包括以下步骤：

(一)、构建基于hermite插值多项式的函数积分求积公式；

基于hermite插值多项式的函数积分求积公式的表达式为：

式中，f(x)为被积函数，h为离散间隔，x为被积函数的自变量，xk为离散点处的离散数值。

(二)、根据铣刀切削时刀具振动的原理建立刀具自由振动起始点与终点的函数关系，构建铣削状态转移矩阵，并获取铣削状态转移矩阵的特征值；

刀具自由振动起始点与终点的函数关系表达式为：

式中，x为刀具振动位移，tf为自由振动的时间段，t0为自由振动的起点时间，t1为自由振动的终点时间，a为典型铣削动力学模型的系数矩阵，模型中b为与铣削力方向系数关联的矩阵、t为时滞周期，即两个刀齿之间的时间间隔。

铣削状态转移矩阵p的表达式为：

式中，w为轴线切削深度，δ为离散间隔，p为状态转移矩阵，各系数矩阵的表达式为：

式中，ti为离散时间点。

(三)、基于floquet理论，根据构建的铣削状态转移矩阵确定铣削系统的稳定性。

铣削系统的稳定性的确定标准为：

式中，λ为铣削状态转移矩p的特征值。

(四)、获取铣削系统的主轴转速ω、轴线切削深度w，将铣削系统的主轴转速ω、轴线切削深度w作为自变量，并将步骤3)确定的铣削系统的稳定性作为因变量，构建铣削系统的稳定性界限图。

与现有技术相比，本发明基于hermite插值多项式的函数求积分公式，对铣削动力学模型的积分解进行近似，同时借鉴时间有限元稳定性分析方法的快速映射关系，构建出快速高效的状态转移矩阵，并借助floquet理论完成状态转移矩阵的稳定性分析，可以在不降低计算精度的前提下，实现对铣削系统稳定性状态获取，并可快速构建出铣削系统的稳定界限，对生产过程中的无颤振铣削加工参数的选择具有重要的意义。

附图说明

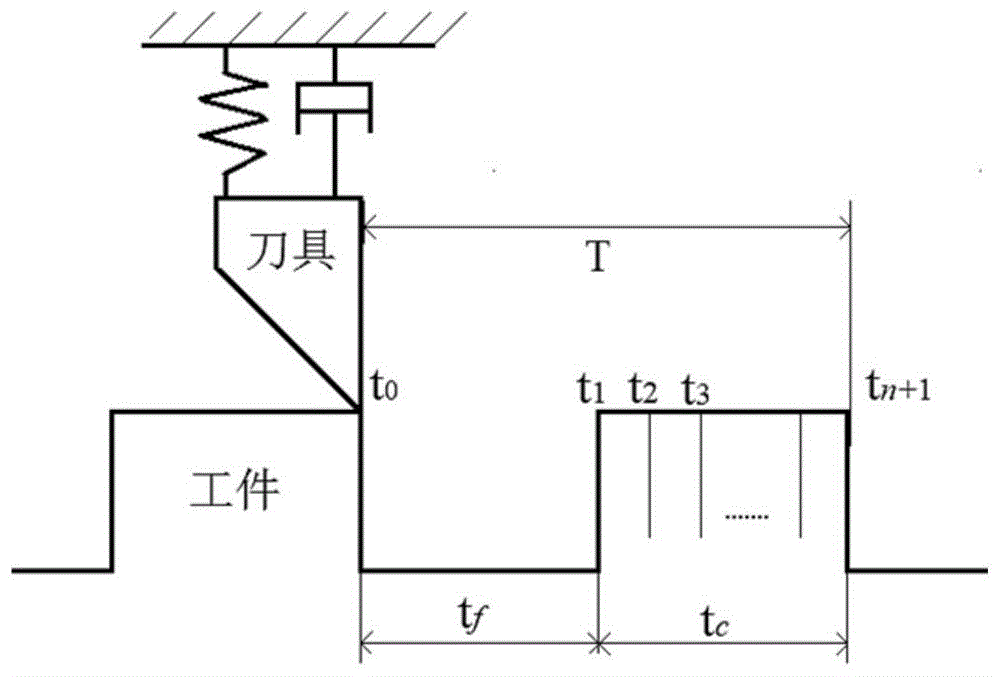
图1为铣削系统中铣刀刀齿切削原理示意图；

图2为实施例中本发明方法与其他四种稳定性分析方法的误差分析对比图；

图3为实施例中本发明方法建立的铣削系统的稳定性界限；

图4为本发明方法的流程示意图。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。显然，所描述的实施例是本发明的一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例，都应属于本发明保护的范围。

如图所示，本发明涉及一种铣削系统稳定性状态获取方法，包括以下步骤：

步骤一、构建基于hermite插值多项式的函数积分求积公式；具体构建内容如下：

假设连续函数为f(x)，估计函数为g(x)，那么g(x)可以被表示为下式：

式中，h为离散间隔的长度，x为被积函数自变量，xk为在离散点k处的数值。

连续函数f(x)可以被近似为下式：

对上式两边求积分得到：

对上式进行近似得到：

构建f′(xk)、f′(xk+1)为：

则代入积分公式可获取：

上式即为基于hermite插值多项式的函数积分求积公式。

步骤二、构建状态转移矩阵，并获取铣削状态转移矩阵的特征值。

1)铣刀切削时刀具振动原理图如图1所示，图中tf为自由振动的时间段，t0是自由振动的起点时间，t1是自由振动的终点时间，tc是切削振动的时间段，t1、t2、t3～tn是切削振动时间段的离散点。t是切削周期。根据铣刀切削时刀具振动的原理建立刀具自由振动起始点与终点的函数关系为：

2)构建铣削动力学模型。

典型的铣削动力学模型为：

模型中b为与铣削力方向系数关联的矩阵、t为时滞周期(即两个刀齿之间的时间间隔)。

式中x为刀具振动位移，且有：

将典型的铣削动力学模型的解用积分形式可表示为：

其中，w是轴向切削深度。

在切削过程中，将[ti,ti+1]的间隔内的解表示为：

根据上式及刀具自由振动起始点与终点的函数关系式可以构建以下映射关系：

其中，c、i、e、d为系数矩阵，且有：

则构建的状态转移矩阵为：

根据上式获取铣削状态转移矩p的特征值λ。

步骤三、基于floquet理论，根据构建的状态转移矩阵确定铣削系统的稳定性。

判定构建的状态转移矩阵确定铣削系统的稳定性的具体标准为：

式中，λ为铣削状态转移矩p的特征值。

步骤四、将铣削系统的主轴转速ω、轴线切削深度w作为自变量，将确定的铣削系统的稳定性作为因变量，构建铣削系统的稳定性界限图。

步骤五、根据获取的铣削系统的稳定界限，对生产过程中的无颤振铣削加工参数进行选择。

未验证本发明方法获取铣削系统的稳定性状态的有效性，本实施例对实际铣削系统进行了实验。

本实施例首先采用模态测试设备获得铣削加工系统的模态质量、模态阻尼、固有频率，并采用测力仪获得材料的切向与径向铣削力系数，构建铣削动力学模型其中铣削系统的参数如下：

切向铣削力系数：ktc＝6×10⁸n/m²；径向铣削力系数：krc＝2×10⁸n/m²；模态质量：0.03993kg；模态阻尼：0.011；固有频率：922hz；本实施例采用逆铣加工。

随后采用经典的半离散方法(sdm，semi-discretizationmethod)作为基准，将图1中切削过程的离散间隔等分为200份，计算在不同铣削参数时本发明方法与半离散方法在200离散间隔时的差值，作为误差值，进行仿真。如图2所示。0sdm、1sdm、1fdm、2fdm分别是0阶次半离散方法、1阶次半离散方法、1阶次全离散方法、2阶次半全散方法时对应的计算误差。从图中可以看出本发明所提方法具有较高的误差并且收敛速度高于其他方法。

根据本发明方法步骤四的内容，采用matlab实现状态转移矩阵的构建，同时将主轴转速ω、轴线切削深度w作为循环变量，利用判定构建的状态转移矩阵确定铣削系统的稳定性的具体标准确定矩阵的稳定性。如图3所示，所提方法与经典sdm法具有高的一致性，即能够保证计算精度。其中m是离散间隔。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的工作人员在本发明揭露的技术范围内，可轻易想到各种等效的修改或替换，这些修改或替换都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权利要求的保护范围为准。