一种任意形状翻滚卫星的非接触式惯量系数辨识方法与流程

本发明属于翻滚目标的姿态估计及参数辨识领域，涉及航天领域的空间在轨服务技术，具体涉及一种任意形状翻滚卫星的非接触式惯量系数辨识方法。

背景技术：

航天器在轨服务的对象多种多样，其中动力失效的卫星或空间碎片占据很大比例。由于失去了动力控制，失效卫星在初始角速度及干扰力矩的作用下一般会陷入绕惯性主轴自由慢翻滚状态，若要对其进行近距离交会、逼近乃至抓捕，必须对其姿态变化规律进行预判，然后选择合适的接近角度靠近，以避免碰撞而导致装置损坏。

为了对翻滚目标未来较长时间的运动状态进行精确预测，以制定更合理的抓捕时机和抓捕路径，必须在抓捕之前使用非接触式的方法对翻滚目标的惯性参数进行准确的辨识。这对于节省抓捕所耗费的时间和燃料、提高抓捕成功率是十分必要的。

对于大部分失效卫星来说由于燃料消耗或结构的损坏等可能会使转动惯量发生变化。在现有技术下利用立体视觉设备或激光测距仪可以在不接触的情况下对未知卫星的姿态信息进行离散测量，但是，在非接触的情况下对卫星的惯性参数进行精确辨识极其困难。目前最常用的参数辨识方法是使用卡尔曼滤波器将其转动惯量作为状态变量之一进行递推拟合，但精度很低，而且需要给定足够精确的角速度测量初值才能保证算法收敛。有文献提出使用常值参数设计滤波器进行辨识，但仅适用于翻滚目标为对称刚体的特殊情况。实际应用中多在抓捕后使用接触的方法对翻滚卫星的转动惯量进行测量，这样虽然简化了任务过程，但会增加额外的能量消耗。

技术实现要素：

本发明的目的在于提供一种任意形状翻滚卫星的非接触式惯量系数辨识方法，以克服上述现有技术存在的缺陷，本发明直接推算出翻滚卫星的惯性参数，即主转动惯量之间的比值。相比于以往的常值估计法，本方法不限于轴对称目标的参数估计，对任意形状的翻滚目标的主转动惯量之间的比值均可进行辨识。

为达到上述目的，本发明采用如下技术方案：

一种任意形状翻滚卫星的非接触式惯量系数辨识方法，包括如下步骤：

1)通过近似方法建立翻滚目标四元数λ的运动方程的近似解；

2)通过近似解提取常值参数作为系统的状态量x；

3)构造扩展卡尔曼滤波器；

4)通过卡尔曼滤波器得到系统的状态量的估计值，并采用估计值估计翻滚卫星的惯性参数。

进一步地，步骤1)具体为：

1-1)建立翻滚目标的姿态四元数的运动学模型：

其中，λ₀,λ₁,λ₂,λ₃为翻滚目标的本体主轴坐标系相对于惯性坐标系的姿态四元数四个分量，ω_x,ω_y,ω_z为目标的角速度在本体坐标系中的投影；

1-2)忽略高频小量，得到翻滚目标的角速度近似解：

其中，ω_xm,ω_ym,ω_zm分别为本体主轴坐标系三个坐标轴方向上的角速度分量的最大值，t为时间，为待辨识的常值参数之一，ε_x,ε_y,ε_z均为该坐标轴方向上的高阶无穷小量；

1-3)使用含有三个特征频率的正弦函数构造描述姿态运动的四元数微分方程的近似解，四元数λ＝[λ₀ λ₁ λ₂ λ₃]^T的解的具体形式为：

λ＝A_4×6ξ (3)

其中A_4×6为4行6列的常数矩阵，且

其中，θ也是待辨识的常值参数；

1-4)将系统的微分方程转化为代数方程，将式(2)与式(3)同时代入式(1)，使用三角函数运算规则合并相同频率项，由三角函数的正则性可知，若等式(1)成立，须令各频率之前的系数均为零，则得到一个由56个算术方程组成的方程组：

其中a为矩阵A_4×6按行展开成向量后生成的行向量，为由θ以及ω_xm，ω_ym，ω_zm决定的常系数矩阵，其各项的具体形式由式(3)推导得到，下标表示矩阵维数，考虑到系统的初值λ(0)，将上式扩展为：

其中，其中常数矩阵D′的值由D′a＝λ(0)推得：

式(4)是约束数大于变量数的超定方程组，使用最小二乘准则求得a，及θ的最小二乘解，得到四元数λ关于时间t的近似解，即姿态四元数随时间变化的近似方程，也就是翻滚目标的姿态运动的近似方程。

进一步地，步骤2)具体为：

实际观测量η为观测坐标系相对于惯性系的四元数，它与λ之间的关系为：

η＝λομ

其中“ο”表示四元数乘法运算；μ为观测坐标系与本体主轴坐标系之间的姿态四元数；

由于四元数乘法不涉及高次项运算，且μ为常数，故η各项均为λ各项的线性组合，由式(3)可知，观测量η同样具有周期性质，即有：

η＝B_4×6ξ (5)

其中B为满足Aξ＝Bξομ的常数矩阵，将矩阵B按行来展开得到行向量b_24×1，并考虑到待辨识的常值参数及θ，共同组成了系统的常值的状态量：

其中，b,θ，均为待辨识的常值参数。

进一步地，步骤3)具体为：

系统的观测方程为

h(x)＝η

将h相对于状态量x求偏导数得到观测敏感度矩阵：

由于系统的状态量均为常值参数，故状态转移矩阵Φ为：

Φ＝Ι_14×14 (7)

其中，I_14×14为14×14的单位矩阵；

由干扰力矩引起的状态量的误差认为是高斯分布的白噪声，则系统过程噪声的方差矩阵Q_k定义为：

Q_k＝σ²Ι_14×14 (8)

其中，σ²为过程噪声的分布方差；

将式(6)-(8)代入卡尔曼滤波器的一般方程，即得到非对称翻滚目标参数辨识的步骤，构造出由待辨识参数作为状态量构成的广义卡尔曼滤波器。

进一步地，步骤4)具体为：

通过卡尔曼滤波器得到状态量x的估计值后，将估计值代入式(4)并求最小二乘解，即得到矩阵D以及角速度参数ω_xm，ω_ym及ω_zm的估计值，并进一步求解得到惯量参数的估计值：：

其中，p_x,p_y,p_z为待辨识的转动惯量比值参数，K为角速度的椭圆函数所对应的第一类完全椭圆积分系数。

与现有技术相比，本发明具有以下有益的技术效果：

(1)该方法使用三个正弦函数近似姿态四元数的运动规律，不局限于特定的解的形式，可以证明该近似方法在所有运动状态下均能取得足够高的精度，因此该方法对目标形状没有限制，适用于任意非对称形状的翻滚目标的参数辨识。(2)该方法用常量参数代替变量参数作为系统的状态参量，使得标称状态下状态参量相对于时间的偏导数为零，当观测的时间间隔较大时，可以显著减小使用数值积分计算的预测值的误差，从而提高惯量参数的估计精度。(3)由于方程具有线性形式，在特征频率θ和的初始值给定较为精确的情况下，对其他初值的精确度没有任何要求，避免了由于初值精度太低而导致的滤波发散现象，提高了惯量参数估计的成功率。使用快速傅里叶变换的数值方法得到θ和的初值，能够保证其精度符合要求。

附图说明

图1为构造四元数动力学方程近似解的流程图；

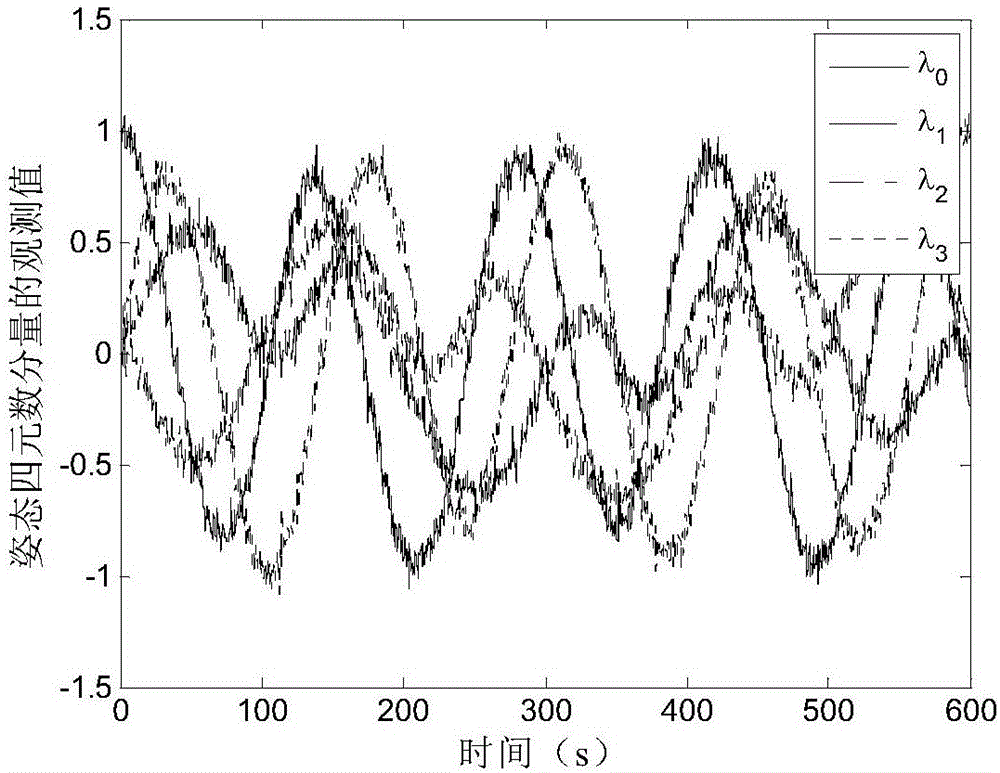
图2为含有噪声的观测数据的实例图；

图3为使用快速傅里叶变化将姿态四元数变化到频域的实例图；

图4为辨识得到的系统运动状态的估计值与预测值随时间变化的轨迹的实例图，其中(a)为观测坐标系对应的四元数分量η₀的轨迹图，(b)为观测坐标系对应的四元数分量η₁的轨迹图，(c)为观测坐标系对应的四元数分量η₂的轨迹图，(d)为观测坐标系对应的四元数分量η₃的轨迹图，(e)为角速度分量ω_x的轨迹图，(f)为角速度分量ω_y的轨迹图，(g)为角速度分量ω_z的轨迹图；

图5为惯性参数估计值的相对误差的收敛过程的实例图。

具体实施方式

下面对本发明作进一步详细描述：

本发明是在非接触的情况对翻滚状态的任意形状的空间碎片或失效卫星的惯性参数进行精确的测算。其主要原理在于：首先选取三个主频率构造含有待定参数的三角函数，作为翻滚目标姿态运动方程的近似解，将这组解代入翻滚目标的四元数姿态动力学方程中，即可将原本的微分方程转化为代数方程，对这组代数方程求解可得以上待定参数的具体值。使用这些待定参数可以代替系统变量表征系统的状态，即翻滚卫星的姿态四元数被表示为关于这些常值参数和时间的函数。翻滚卫星的姿态四元数可以通过现有的技术手段进行测量，本方法通过线性最小方差估计，对待定参数的值进行实时的估计，且随着观测量的增加，估计精度越来越高。利用这些待定参数的值，本方法直接推算出翻滚卫星的惯性参数，即主转动惯量之间的比值。相比于以往的常值估计法，本方法不限于轴对称目标的参数估计，对任意形状的翻滚目标的主转动惯量之间的比值均可进行辨识。

本发明的方法具体包括以下步骤：

步骤一：通过近似方法建立翻滚目标四元数运动方程的近似解，如图(1)所示。具体流程为：首先建立翻滚目标的姿态四元数的运动学模型

其中，λ₀,λ₁,λ₂,λ₃为翻滚目标的主轴坐标系相对于惯性系的姿态四元数四个分量，ω_x,ω_y,ω_z为目标的角速度在本体主轴坐标系中的投影；

忽略高频小量，写出翻滚目标的角速度近似解

其中ω_xm,ω_ym,ω_zm分别为本体坐标系三个坐标轴方向上的角速度分量的最大值，t为时间，为待辨识的常值参数之一，ε_x,ε_y,ε_z均为该坐标轴方向上的高阶无穷小量，ε为高频项，其对于角速度的长期影响为零。

通过频域分析可以发现四元数随时间变化的函数在频域中有三个明显的尖峰，因此使用含有三个特征频率的正弦函数构造描述姿态运动的四元数微分方程的近似解。四元数λ的解的具体形式为

λ＝A_4×6ξ(3)

其中A_4×6为4行6列的常数矩阵，且

其中θ与也为待识别的常值参数，且的值仅由角速度特性决定。

将系统的微分方程转化为代数方程。将式(2)与式(3)同时代入式(1)，使用三角函数运算规则合并相同频率项，由三角函数的正则性可知，若等式(1)成立，须令各频率之前的系数均为零，则得到一个由56个算术方程组成的方程组

其中a为矩阵A_4×6按行展开成向量后生成的行向量，为由θ以及ω_xm，ω_ym，ω_zm决定的常系数矩阵，其各项的具体形式由式(3)推导可得，下标表示矩阵维数。考虑到系统的初值λ(0)，上式可扩展为

其中，其中常数矩阵D′的值由D′a＝λ(0)推得：

式(4)是约束数大于变量数的超定方程组，可使用最小二乘准则求得a，及θ的最小二乘解，得到四元数λ关于时间t的近似解，即姿态四元数随时间变化的近似方程，也就是翻滚目标的姿态运动的近似方程。事实上，由于自由翻滚目标的角速度满足Jacobi椭圆函数积分的形式，高频项系数很小，因此以此方法确定的近似解具有较高的精度。

步骤二：提取常值参数作为系统的状态量。考虑到实际观测量η为观测坐标系相对于惯性系的四元数，它与λ之间的关系

η＝λομ

其中“ο”表示四元数乘法运算，μ为观测坐标系与本体主轴坐标系之间的姿态四元数。由于四元数乘法不涉及高次项运算，且μ为常数，故η各项可均为λ各项的线性组合。由式(3)的形式可知，观测量η同样具有周期性质，即有

η＝B_4×6ξ (5)

其中B为满足Aξ＝Bξομ的常数矩阵。将矩阵B按行来展开得到行向量b_24×1，并考虑到待辨识的常值参数及θ，共同组成了系统的常值的状态量x

b,θ，均为待辨识的常值参数；

步骤三：构造扩展卡尔曼滤波器。

系统的观测方程为

h(x)＝η

将h相对于状态量x求偏导数得到观测敏感度矩阵

由于系统的状态量均为常值参数，故状态转移矩阵Φ为单位矩阵

Φ＝Ι_14×14 (7)

其中，I_14×14为14×14的单位矩阵；

由干扰力矩引起的状态量的误差认为是高斯分布的白噪声，则系统过程噪声的方差矩阵Q_k定义为

Q_k＝σ²Ι_14×14 (8)

其中，σ²为过程噪声的分布方差；

将式(6)-(8)代入卡尔曼滤波器的一般方程，即得到非对称翻滚目标参数辨识的步骤。与对称目标的情况类似，状态量中b向量的各项满足线性形式，不需要给定精确的初值。而θ与涉及三角函数运算，因此需要使用离散傅里叶变换确定特征角频率θ和的初值。

步骤四：通过卡尔曼滤波器得到状态量x的估计值后，将估计值代入式(4)并求最小二乘解，即可得到矩阵D以及角速度参数ω_xm，ω_ym及ω_zm的估计值。进一步，由下式计算转动惯量参数的估计值

p_x,p_y,p_z为待辨识的转动惯量比值参数，K为角速度的椭圆函数所对应的第一类完全椭圆积分系数。

为了更好地说明本发明的目的和优点，下面结合附图和实例对本发明内容做进一步说明：

设翻滚目标在空间中作自由漂浮运动，使用立体视觉设备或激光测距仪可以测得姿态四元数四个变量随时间变化的函数，如图2所示。由于干扰力矩和观测误差的影响，测量结果是受噪声污染的。应用本方法，可以利用这些观测噪声实时地估计出该翻滚卫星的惯性参数p_x，p_y及p_z，具体包括以下步骤：

步骤一：先使用快速傅里叶变换算法将λ₀(t)的部分数据变化到频域，如图3所示。频域中有三个尖峰，将中间尖峰的横坐标的值赋给θ，尖峰横坐标之间的间隔赋给作为初值。x中其他参数的初值被赋为0。

步骤二：以x为状态参数，以姿态四元数λ的实时观测量为输入，构建卡尔曼滤波器，逐步估计出状态参数更精确的值。如图4所示，由常值参数的估计值计算并预测得到的姿态四元数及角速度的误差均小于直接观测值的误差。

步骤三：利用x各参数的值计算翻滚卫星惯量参数p_x，p_y及p_z的值，其估计值随时间变化曲线如图5所示，可见惯性参数的估计值随着观测量的增加而趋近真实值。

本实例中采用的系统参数的值如表1所示：

表1.实例采用的系统参数值