一种稀疏约束抛物Radon变换方法与流程

本发明涉及地震数据处理技术，主要用于数据规则化、多次波消除、去噪等领域，主要特点是利用一种稀疏约束抛物radon变换方法。

背景技术：

radon变换最早是由奥地利数学家j.radon于1917年提出的[1]，为物理学、医学、天文学、分子生物学、材料科学、光学、核磁共振、无损检测技术和地球物理学中的一大类图像重建(层析)问题提供了统一的数学基础。radon变换在地震资料处理中的应用非常广泛，特别是在地震数据插值和多次波压制领域。

和通常的数学变换，比如傅里叶变换和小波变换不同，radon变换算子不是正交化的。因此，在不丢失数据的前提下进行正反radon变换是一个很重要的问题。radon变换可以通过很多方法推导出来，但最常见的还是反演方法。通过使预测数据和观测数据的误差在最小二乘意义下最小，以及模型长度最短的约束条件得到反演结果。

由于观测数据的离散采样和误差，反演过程存在着解的非唯一性问题。除此之外，有限孔径还带来了分辨率降低的问题。通过误差在最小二乘意义下最小和模型长度最短约束反演过程，这个过程导出的是非稀疏radon变换，得到的是一个分辨率很低的模型。因为稀疏反演能够极大地提高反演解的精度，得到一个高分辨率的模型，所以有必要在反演过程中引入稀疏化约束。应用稀疏化在带来了好处的同时也带来了新的问题，计算时间的增加，解的不稳定和反演参数的取舍。因为稀疏radon变换对反演过程中选取的规则化参数十分敏感，参数的选择依赖于求取的问题，而且对反演的结果影响非常大。在频率域中这个问题更严重，因为每个频率的参数都是重新选择的，在该参数下反演这个频率的解。如果某个频率的参数选取有误，那么整个radon域的结果都要受影响。

技术实现要素：

本发明的目的是要提供一种稀疏约束抛物radon变换方法，能够较好解决由于数据采样不足、孔径不足等对radon变换谱的影响，提高谱的聚焦性。从而能够提高基于radon谱方法的多次波消除、数据规则化、去噪等处理的效果。

为达到上述目的，本发明是按照以下技术方案实施的：

一种稀疏约束抛物radon变换方法，包括以下步骤：

(1)令d(x,t)为采集的cmp道集，m(v,τ)为radon模型空间；

(2)进行t²拉伸变换，将d(x,t)中数据变换到d(x,t')(t'＝t²)，从而使双曲线时距关系变为抛物线；

(3)进行fourier变换得到

(4)对一特定的频率ω'，

(a)根据公式计算抛物radon逆变换算子g^t，其中偏移距与cmp道集中的偏移距相对应，速度v则选取用来做叠加的速度(选取一个最小值vmin和一个最大值vmax)；

(b)在中抽取向量长度为nx；

(c)使用共轭梯度法求解公式得到长度为nv；

(d)由公式求得

(e)返回步骤(4)对所有频率ω'重复步骤(4)，将(c)中得到的数据存放到(d)中得到的数据存放到

(5)分别对做fourier反变换，得到m(v,τ')，d'(x,t')；

(6)分别对m(v,τ')，d'(x,t')做反t²拉伸变换，得到m(v,τ)，速度谱模型空间和d'(x,t)，重建后的数据空间。

与现有技术相比，本发明的有益效果为：

1、同时引入了对数据的低频加权和对模型的稀疏约束，能够对同时对空间假频较好的抑制和模型的稀疏性较好的保持；

2、本发明抛物radon变换能够较好的利用快速算法，保证较高的计算效率。

附图说明

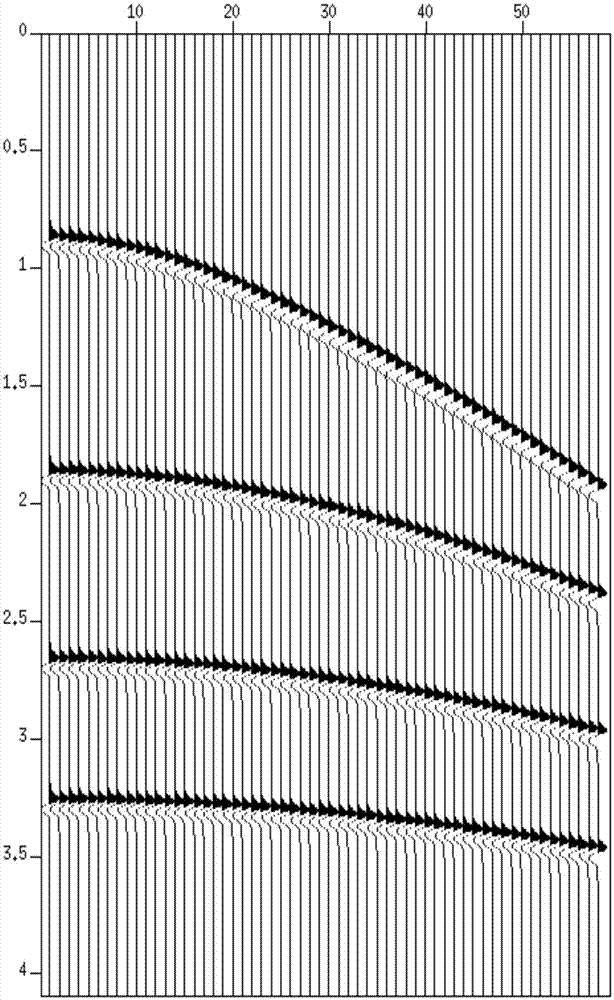
图1是一个合成的cmp道集。

图2a是常规方法得到的抛物radon结果；图2b为常规抛物radon变换后重建的cmp道集。

图3a为本发明得到的抛物radon结果，图3b为重建的cmp道集。

图4a为marmousi模型一个cmp道集，图4b为该marmousi模型中间人为去掉了4道地震数据。

图5为利用本发明radon变换恢复4道地震数据后的道集，以及两者的差。

具体实施方式

下面结合具体实施例对本发明作进一步描述，在此发明的示意性实施例以及说明用来解释本发明，但并不作为对本发明的限定。

本发明的一种稀疏约束抛物radon变换方法，包括以下步骤：

如图1所示，设d(x,t)为采集的cmp数据空间，m(v,τ)为模型空间(radon空间)，对水平层状介质而言，反射地震波的时距曲线可以近似的表示为一条中心在零偏移距的双曲线：

其中t表示地震波的双程旅行时，τ表示零偏移距时地震波的双程旅行时，v表示均方根速度。

若沿着双曲线(1)对数据空间进行积分，就可以得到双曲radon变换的表达式：

写为离散形式有：

同样的，在模型空间对v沿曲线进行积分，可以得到反双曲radon变换的表达式：

写为离散形式有：

由(3)，(5)两式可以看出t与τ呈非线性的关系，要进行双曲radon变换必须给定一个比较精确的速度函数v(t)，对(3)，(5)式的求解是时变的，不能应用快速算法，所以解这样的方程需要耗费大量的时间，代价是昂贵的。

现在，我们对(1)两边平方，并令t'＝t²，τ'＝τ²，则(1)变为：

如图2a所示，可见d(x,t)中数据的时距关系在d(x,t')中呈抛物线分布，将(6)代入(3)，(5)两式，得到d(x,t')空间中的radon变换的正反表达式：

这里积分曲线是抛物线，所以(7)，(8)即是抛物radon变换的正反表达式。由(7)，(8)式可以看出，t'与τ'是呈线性关系，时不变的，因此可以对(7)式做τ'方向的fourier变换，则有：

写为矩阵形式有：

其中是长度分别为nv，nx的复向量，矩阵g^t是抛物radon正变换算子：

同理，我们可以得到反变换的矩阵表达式：

其中，g是radon逆变换算子：

可见，g与g^t互为共轭转置矩阵。

综上所述，抛物radon正反变换可以抽象为求解矩阵方程：

由于抛物radon变换是对每一个频率ω'做的，即将双曲radon变换需要求解的大矩阵化为若干个小矩阵，求解这种小矩阵要容易很多，并且可以应用快速算法。

如图2b所示，可以看出，由于泄露能量的影响，不能很好的恢复数据，为了克服直接求取得到的模型空间分辨率低的问题，常见的做法是将求取模型空间m(v,ω')视为一个反问题，即利用(14)式：

现在，我们的目的是要找到一个合适的模型空间使得重建后的数据空间与原始数据空间的差异在最小二乘的意义下达到最小。

设j为误差泛函，则有：

我们重新定义误差泛函，并引入模型权重矩阵，用稀疏化准则约束模型，提高分辨率：

wm是模型权重矩阵，它是一个对角阵，可以通过改变对角线上元素的值调整模型的光滑或者稀疏程度。模型权重矩阵wm能够把数据空间中的反射同相轴聚焦到模型空间中的一个点上，即通过稀疏准则约束模型，从而大大地提高了模型的分辨率。

除了要提高分辨率之外，防止假频的出现也是一个很重要的问题。我们知道由于采样密度的限制，数据在nyquist频带范围内能保证没有假频，超过了nyquist频率由于频谱混叠就会出现假频现象。所以要在反演过程中也加入约束来防止假频出现。因为数据在低频时是充分采样的，不会出现假频，这启发我们用低频段的数据约束高频数据。为此改写误差泛函jnew，在其中引入数据权重矩阵：

把j'new对求导，则有：

令导数为0，则有：

故有：

下面，以数据插值的为例说明本发明实现流程：

(1)抽取cmp道集，得到数据空间d(x,t)；

(2)进行t²拉伸变换，将d(x,t)中数据变换到d(x,t')(t'＝t²)，从而使双曲线时距关系变为抛物线；

(3)进行fourier变换得到

(4)对一特定的频率ω'：

(a)根据(12)式计算抛物radon逆变换算子g^t，这里偏移距要与cmp道集中的偏移距相对应，速度v则选取用来做叠加的速度(选取一个最小值vmin和一个最大值vmax)；

(b)在中抽取向量长度为nx；

(c)使用共轭梯度法求解式(15)，得到长度为nv；

(d)由(13)式求得

(e)返回(4)对所有频率ω'做上述步骤，将(c)中得到的数据存放到(d)中得到的数据存放到

(5)分别对做fourier反变换，得到m(v,τ')，d'(x,t')；

(6)分别对m(v,τ')，d'(x,t')做反t²拉伸变换，得到m(v,τ)，模型空间(速度谱)和d'(x,t)，重建后的数据空间。

参照图3a、图3b、图4a、图4b、图5，图3a为本发明得到的抛物radon结果，图3b为重建的cmp道集，可以看出本发明能够很好的重建数据。图4a为marmousi模型一个cmp道集，图4b为该模型中间人为去掉了4道地震数据。图5左中右分别为原始cmp道集，利用本发明radon变换恢复4道地震数据后的道集，以及两者的差，可以看出，本发明方法能够较好的恢复缺失的地震道。

本发明的技术方案不限于上述具体实施例的限制，凡是根据本发明的技术方案做出的技术变形，均落入本发明的保护范围之内。