一种有机材料的韧性、强度和弹性的测算方法与流程

本发明属于材料特性测量
技术领域：
，具体涉及材料的韧性，强度和伸缩性(或弹性)的测算方法。
背景技术：
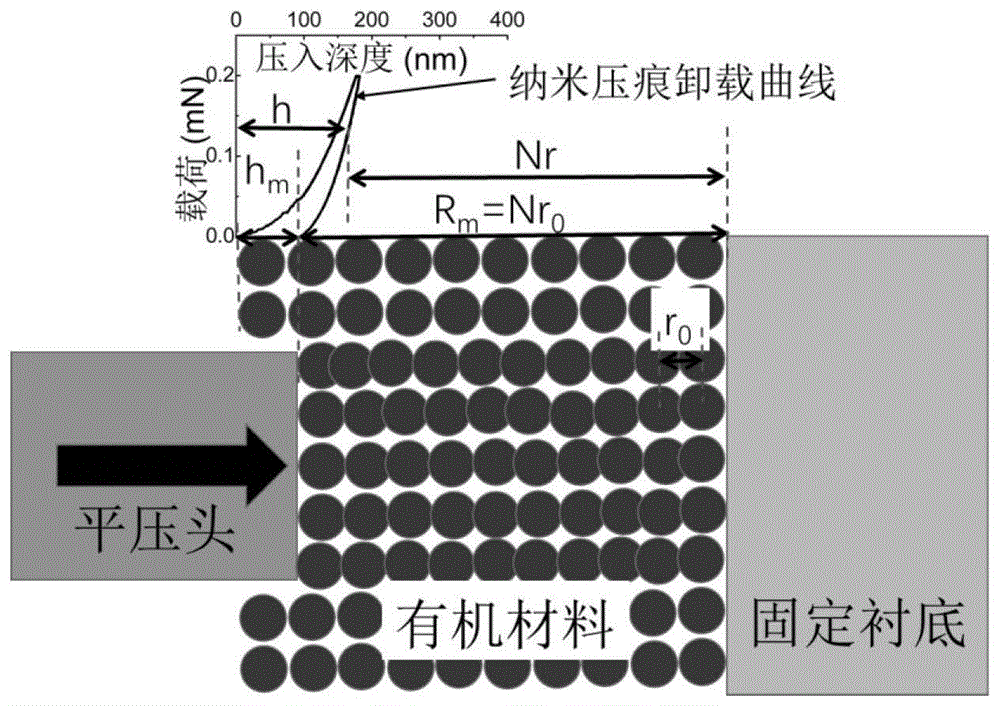
：随着有机电子学的应用，有机发光二极管、有机太阳能电池、印制电路、可穿戴设备和智能机器人的发展，有机薄膜材料的机械性能越来越受到关注。目前，纳米机械测试系统(或纳米压痕测试仪)是一种用于测试材料力学性能的先进工具。然而，大多数研究人员对纳米压痕测试得到的加载-卸载曲线的理解仍然仅与宏观力学特性有关，而内在的物理原理大多数仍然含糊不清，我们认为加载-卸载曲线反映了有机薄膜中两个相邻分子的距离与作用力之间的关系，而且分子间距离和分子间力之间的关系可以用罗纳德-琼斯(lennard-jones)势来描述。因此，本发明使用罗纳德-琼斯势理论来推导和拟合卸载曲线，并通过卸载曲线的拟合参数获得五个重要的机械性能参数。材料的这些机械性能包括表示刚度的杨氏模量，表示强度的结合力，表示韧性的结合能，以及表示弹性或伸缩性的，从平衡位置到具有最大拉伸应力位置的距离。通过本发明方法，可以开发出更加方便实用的工具来测试材料的多种机械性能，具有良好的应用前景。技术实现要素：本发明的目的在于提供一种新的用于测试材料强度、韧性和弹性的测算方法。本发明提供的够反映材料本身力学特性、排除干扰因素、便于比较不同材料之间力学特性的材料强度、韧性和弹性的测算方法，具体步骤为：(1)利用纳米压痕仪对通过范德华力结合的材料，例如大部分有机材料，进行单次加载-卸载测试，得到该材料单次的纳米压痕载荷曲线；(2)应用描述分子间力和分子间距关系的罗纳德-琼斯势理论，推导得到卸载曲线中的载荷与压入深度的函数关系，利用该函数对载荷曲线进行计算机软件运算的最优化拟合，得到最佳拟合参数；(3)根据罗纳德-琼斯势理论推导得到表征材料强度、韧性和弹性的关系式，把上述步骤得到的最佳拟合参数代入这些关系式中，计算得到反映材料强度、韧性和弹性的力学性能参数。本发明步骤(2)中，根据罗纳德-琼斯势推导得到的，用于拟合卸载曲线的公式为：式中，f为卸载曲线中的载荷，h为卸载曲线中的压入深度，hm为受力为零时的压入深度，ε为待拟合的参数：分子间相互作用势能最低点的数值，rm为待拟合的参数：实际参与形变的薄膜在平衡状态下的厚度。步骤(3)中，所述卸载曲线中，表征材料韧性的公式为：式中，vb为材料的单位面积结合能，ε为通过卸载曲线拟合得到的参数，代表势能曲线的最低点，反映了分子之间吸引势的绝对值。d为纳米压痕测试所用平压头的直径。把卸载曲线拟合得到的参数代入上式即可得到材料韧性参数的数值。步骤(3)中，所述卸载曲线中，表征材料强度的公式为：式中，fb为材料的单位面积结合力，反映了材料分子之间最大的拉伸应力。ε为通过卸载曲线拟合得到的参数，代表分子之间势能曲线的最低点，反映了分子之间吸引势的绝对值。d为纳米压痕测试所用平压头的直径。rm为卸载曲线拟合得到的参数，代表测量过程中所有参与形变有机材料在卸载后的平衡状态下的总厚度。把卸载曲线拟合得到的参数代入上式即可得到材料强度参数的数值。步骤(3)中，所述卸载曲线中，表征材料伸缩性能的公式为：lb＝0.109rm式中，lb为材料从平衡状态下拉伸到最大拉伸应力时所需要通过的位移。rm为卸载曲线拟合得到的参数，代表测量过程中所有参与形变有机材料在卸载后的平衡状态下的总厚度。把卸载曲线拟合得到的参数代入上式即可得到材料伸缩性参数的数值。本发明的优势在于：这种新的材料强度、韧性和弹性的力学性能参数测算方法测试和计算都更加方便，且能够反映材料本身的力学特性，排除了很多干扰因素，更适合用来比较不同材料之间的力学特性，对发展材料力学性能的测量方法和开发测量工具，都具有重大意义。本发明方法适用于测试比较疏松的有机材料的力学参数，尤其适用于测试具有范德华力(分子力)相互作用的材料的力学参数。可以建立一种使用方便、测量准确、应用范围广泛的材料力学标准化测试方法和测试工具。附图说明图1为纳米压痕装置示意图和测得的加载-卸载曲线。图上部为实际纳米压痕测试获得的载荷曲线。可见施加在材料上的力随压入深度加深而加大，包括加载，保载和卸载三个过程。卸载曲线通常能基本反映材料本身的固有机械性能。图左下部可见向材料表面压入(压力向右)的平压头示意图，中间可见被压入的材料薄膜。压入深度为h。卸载后载荷为零(表示分子处于平衡状态)时的压入深度为hm。假设n个分子层参与变形，而固定的衬底不参与变形。分子之间的总距离为nr，其初始值为nr0，可以假设为rm。分子间实际距离为nr＝rm-(h-hm)。图2为利用纳米压痕仪测量的聚甲基丙烯酸甲酯(polymethylmethacrylate)，pmma)薄膜的渐进多次测试的载荷曲线，可以从中发现合适的加载压力范围；插图显示压入深度(黑色，即上方曲线)和作用力(蓝色，即下方曲线)随时间的变化，可以看出材料是否存在蠕变或塑性变形。图3为在1.2mn的最大应力下，单次测试中测得的pmma薄膜的加载-卸载曲线；插图显示了较大应力下(最大为10mn)的载荷曲线。较粗的红色曲线是通过电脑软件自动最优化拟合得到的卸载曲线。具体实施方式实施例1下面以聚甲基丙烯酸甲酯(polymethylmethacrylate)，pmma)有机薄膜为例并结合附图进行进一步说明。图1为纳米压痕装置示意图和纳米压痕仪测得的加载-卸载曲线，可以帮助理解载荷曲线和拟合参数的物理意义。图2为利用纳米压痕仪测量的pmma薄膜的渐进多次测试的载荷曲线，可以从中发现合适的加载压力范围；插图显示压入深度(黑色)和作用力(蓝色)随时间的变化，可以看出材料是否存在蠕变或塑性变形。图3细线为较小压力(最大为1.2mn)下测得的载荷曲线。红色粗线为拟合得到的载荷曲线，插图为较大压力下测得的载荷曲线，插图显示较大压力(1.5～10mn)下受到刚性的衬底影响而显示出刚度比较高，但在较小压力下(小于1.5mn)不呈现塑性变形。图中可见拟合曲线和实验曲线重合度很高。拟合卸载曲线所用的方程为：通过设置该拟合方程，用数据处理软件进行最优化自动拟合以后，得到以下三个参数：(1)(2)hm＝31.645nm；(3)rm＝690nm。把这三个参数分别代入表征材料韧性、强度和弹性的公式中，得到：(1)pmma的韧性参数：单位面积结合能：vb＝95.454mj/m2；(2)pmma强度参数：单位面积结合力：fb＝1.4885mpa；(3)pmma弹性(伸缩性)参数：材料从平衡状态下拉伸到具有最大拉伸应力时通过的位移：lb＝75.21nm。我们比较了六种常见的有机薄膜材料的四种力学参数(韧性、强度、刚度和弹性)，如下表所示。这六种材料为：聚乙烯(polyethylene,pe)、聚丙烯(polypropylene,pp)、聚甲基丙烯酸甲酯(polymethylmethacrylate,pmma)、聚四氟乙烯(polytetrafluoroethylene,ptfe)、聚对苯二甲酸乙二醇酯(polyethyleneterephthalate,pet)、聚酰亚胺(polyimide,pi)。纳米压痕卸载曲线拟合得到的六种有机材料的四种力学参数参数材料petpipmmapppeptfevb(mj/m2)15828.031496.8295.45411.460.69750.2252fb(mpa)10.63693.3441.48850.56050.52230.072e0(mpa)11.211.8906.542.860836.1lb(nm)436001308075.21599.539.2492.65注:此处泊松比"υ"设为0，压头直径20微米。上述实施例说明了本发明的可行性及先进性。另外，该实施例仅用以解释本发明，并不用于限定本发明。当前第1页12