一种融合空间相关性的地理数据支持向量回归方法与流程

本发明涉及地理空间信息非线性回归分析领域，尤其是一种融合空间相关性的地理数据支持向量回归方法。
背景技术：
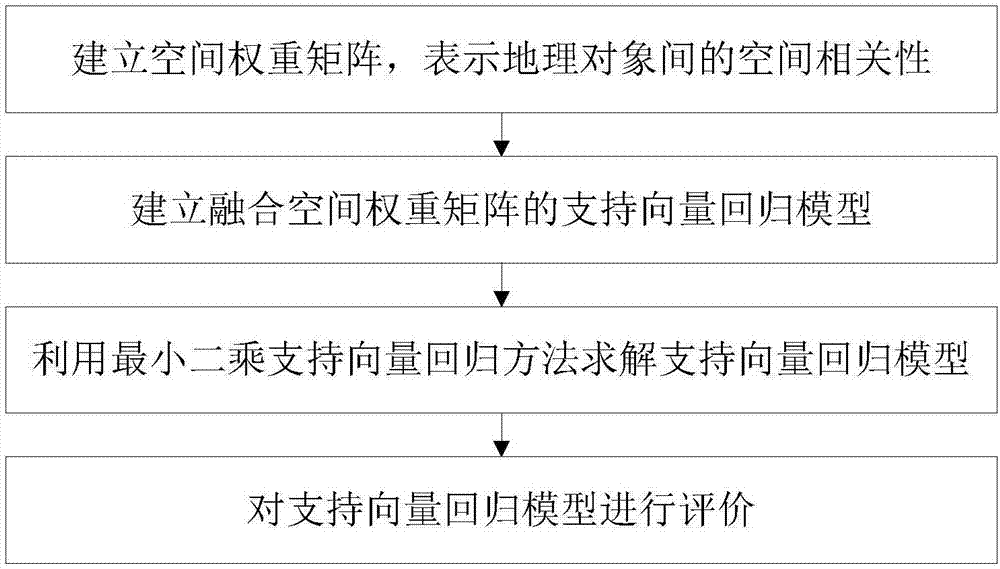
：地理数据是指包括资源、环境、经济和社会等诸多领域的一切带有地理坐标的数据。地理数据是地理对象的空间特征和属性特征的数字描述，地理对象的空间特征表现为自身的位置、形状、大小及分布特征等几何(定位)特征和对象之间的空间关系，地理对象的属性特征则表现为对象的数量特征、质量特征和时间特征。地理数据对地理对象空间特征的描述，不仅可以表达空间位置信息，而且可以表达空间相关性、异质性、顺序关系、度量关系和拓扑关系等信息。如何综合考虑地理对象的空间特征和属性特征解决实际问题是进行地理空间分析和应用的关键。从数据分析角度，统计是面对数据而又缺乏相应机理方法时的主要手段之一。传统统计方法基于大数定律，研究的是渐进理论，即在样本数量足够多的前提下进行研究。也就是说，只有在样本数量趋于无穷大的极限条件下，统计特征才有理论上的保证，才符合统计学的部分推论。显然，实际问题并不满足这样的前提条件，样本数量通常都是有限的。除此之外，传统统计方法和基于统计学习理论的机器学习方法大多基于样本独立同分布的假设基础，当地理对象作为统计分析样本时也应满足同样的假设条件，即地理对象应相互独立、彼此之间没有相关性且服从同一随机分布。但实际上，按照地理学第一定律，地理对象的空间特征和属性特征总是存在着或多或少的相关性，表现为聚集、随机、规则等多种可能分布形态；美国学者michaelfrankgoodchild将空间异质性概括为地理学第二定律，认为地理对象的特征分布在地理空间上是不平稳的、具有差异性，在不同的空间位置可能服从不同的随机分布。因此，地理空间数据的本质特征是与传统统计学基本假设相驳的。综上所述，面向常规数据且未考虑空间特征的传统统计方法并不完全适用于地理数据的统计分析，无法有效、准确地解决实际地理问题，例如：对于地理数据的线性回归，最小二乘估计结果通常是有偏的。对于样本数量受限情况，统计学习理论是研究小样本学习的经典理论，能够在有限样本条件下进行学习，均衡精度和泛化能力。因此，将传统统计方法、基于统计学习理论的机器学习方法与地理数据的空间特征、属性特征相结合，实现地理数据的统计分析和建模，是空间数据分析的研究目标。技术实现要素：本发明的目的是为克服上述现有技术的不足，提供一种融合空间相关性的地理数据支持向量回归方法。为实现上述目的，本发明采用下述技术方案：一种融合空间相关性的地理数据支持向量回归方法，包括以下步骤：步骤一：建立空间权重矩阵，表示地理对象间的空间相关性；步骤二：建立融合空间权重矩阵的支持向量回归模型；步骤三：利用最小二乘支持向量回归方法求解支持向量回归模型；步骤四：对支持向量回归模型进行评价。优选的，所述步骤一中，所述空间权重矩阵采用0-1型或数值型进行表达，0-1型空间权重矩阵元素值wij取0或1，数值型权重矩阵元素值wij取一般数值。n个地理对象{s1,s2,…,sn}的空间权重矩阵w大小为n×n。进一步优选的，建立空间权重矩阵包括标准化步骤，权重矩阵各行元素之和为1。优选的，所述融合空间权重矩阵的支持向量回归模型形式为：设地理区域s内有n个空间对象s＝{s1,s2,…,sn}，其中地理对象si的坐标或中心坐标为(pi,qi)，m维属性向量为attr(si)＝[ai1,ai2,…,aim]；当地理对象si(i＝1,2,…,n)的某一属性变量依赖于其它d个属性变量取值时，其中d<m，则前面的属性变量称为依赖变量，记为yi，后面的d个属性变量称为解释向量，记为xi＝[aik,…]，其中k∈{1,2,…,m}；给定n个地理对象{si}的观测数据集{(xi,yi)}，xi∈rd，yi∈r，则融合空间权重矩阵的支持向量回归模型形式为：其中，ω表示权系数向量；表示输入空间到特征空间的映射函数；b表示常数项；i表示单位阵；w表示行标准化后的空间权重矩阵；x＝[x1,x2,…,xn]t；ρ表示x与wx的相关系数。进一步优选的，ρ由下式确定：其中，cov(y,wy)表示n个地理对象的因变量y＝[y1,y2,…,yn]t与空间相关对象的因变量wy的协方差；σy、σwy分别表示y、wy的标准差。优选的，所述步骤三具体步骤为：1.依据统计学习理论，支持向量回归模型的目的是使结构风险和经验风险同时达到最小，将融合空间权重矩阵的支持向量回归模型转换为优化函数：其中，表示结构风险，结构风险描述支持向量回归模型的复杂度，表示经验风险，经验风险描述支持向量回归模型与观测数据的拟合程度，在最小二乘支持向量回归方法中，经验风险用误差平方和表示，ei∈r表示误差项，γ表示正则化参数；在最小二乘支持向量回归方法中，误差项ei等于观测数据yi与回归模型计算值之差，因此优化函数须满足约束条件：2.利用拉格朗日函数最优解求解优化函数，获取最终的融合空间权重矩阵的支持向量回归模型，具体表达为：其中，k(xi，x)是核函数。进一步优选的，所述步骤2中，利用拉格朗日乘子法将步骤1中含约束条件的优化函数转化为无约束条件的拉格朗日函数，所述拉格朗日函数为：其中αi是拉格朗日乘子；根据kkt条件，所述拉格朗日函数最优解条件为：则融合空间权重矩阵的支持向量回归模型为：其中，k(xi，x)是核函数。优选的，所述步骤四中，采用均方误差、动态相似率两种评价指标对融合模型的回归性能进行度量。本发明的有益效果是，本发明克服了常规支持向量回归模型未考虑地理对象空间相关性之不足，以空间权重矩阵形式将空间相关性与支持向量回归模型相结合，并利用最小二乘支持向量回归算法对模型求解，与常规ls-svr模型相比，该方法不仅拟合精度更高，而且与真实值的变化趋势更接近。附图说明图1是本发明流程图；图2(a)-图2(c)分别是一阶邻接型空间权重矩阵的rook邻接、bishop邻接及queen邻接；图3(a)-图3(b)分别是二阶邻接型空间权重矩阵的rook邻接、queen邻接；图4是输入空间、特征空间和地理空间三者之间的关系；图5是columbuscrime数据集属性变量crime的moran’si散点图；图6是columbuscrime数据集属性变量crime的moran’si指数相应的z得分值和p值概率分布情况；图7(a)是columbuscrime数据集测试数据因变量crime的真实值和常规ls-svr模型计算输出值对比图；图7(b)是columbuscrime数据集测试数据因变量crime的真实值和融合空间相关性的geols-svr模型计算输出值对比图；图8是bostonhousing数据集属性变量medv的moran’si散点图；图9(a)是bostonhousing数据集测试数据因变量medv的真实值和常规ls-svr模型计算输出值对比图；图9(b)是bostonhousing数据集测试数据因变量medv的真实值和融合空间相关性的geols-svr模型计算输出值对比图；图10是elect数据集属性变量castingvotesratio的moran’si散点图；图11(a)是elect数据集测试数据因变量castingvotesratio的真实值和常规ls-svr模型计算输出值对比图；图11(b)是elect数据集测试数据因变量castingvotesratio的真实值和融合空间相关性的geols-svr模型计算输出值对比图。具体实施方式下面结合附图和实施例对本发明进一步说明。设地理区域s内有n个空间对象s＝{s1,s2,…,sn}，其中对象si的坐标或中心坐标为(pi,qi)、m维属性向量为attr(si)＝[ai1,ai2,…,aim]。当地理对象si(i＝1,2,…,n)的某一属性变量依赖于其它d个(d<m)属性变量取值时，则前面的属性变量称为依赖变量(即因变量)，记为yi，后面的d个属性变量称为解释向量(即自变量)，记为xi＝[aik,…]，其中k∈{1,2,…,m}。给定n个地理对象{si}的观测数据集{(xi,yi)}，xi∈rd，yi∈r，回归函数y≈f(x)代表因变量y和自变量x之间的依赖关系，其中x＝[x1,x2,…,xn]t、y＝[y1,y2,…,yn]t。对于地理数据的回归建模，由于地理学第一定律阐述的空间相关/关联现象的普遍性，地理对象si的因变量属性yi的变化不仅依赖于对象本身自变量属性xi的变化，还依赖于其它地理对象sj的自变量属性xj、因变量属性yj的变化，则融合空间相关性的地理数据回归函数的一般形式可表述为：yi≈f(xi,xj,yj)i＝1,2,…,n；j∈[1,2,…,n]且sj与si具有空间相关性(1)任意两个地理对象si与sj之间的空间相关程度可通过空间权重矩阵wn×n定量度量。具体来说，对于si，其它对象sj(j＝1,2,…,n且j≠i)与其的相关程度通过空间权重矩阵的元素wij体现，wij值越大则相关性越高、值越小则相关性越差、值为0则没有相关性。公式(1)需考虑空间相关对象sj的xj、yj因素影响，相关性高的对象影响因素大、相关性低的对象影响因素小，则wij可作为度量sj的xj、yj对si的因变量yi影响因素大小的权重因子。考虑所有sj对同一si的影响因素，则类似空间插值的反距离权重法idw(inversedistanceweighting)，对于对象si，应对所有相关对象sj的权重因子进行标准化处理，使所有权重因子之和为1，即也就是需对空间权重矩阵进行行标准化处理。那么，公式(1)的一般形式可进一步表述为：yi≈f(xi,wijxj,wijyj)(2)融合空间相关性的地理数据支持向量回归方法就是采用类似wx、wy的形式在支持向量回归模型的回归函数中融合空间相关性，从而既保持了支持向量机自身的优良特性，又体现了地理数据的空间相关性特征。如图1所示，一种融合空间相关性的地理数据支持向量回归方法，包括以下步骤：步骤一：建立空间权重矩阵，表示地理对象间的空间相关性；设研究区域有n个地理对象{si}，那么空间权重矩阵w是一个n×n矩阵，元素wij(i＝1,2,…,n；j＝1,2,…,n且j≠i)表达和度量si和sj之间的空间关系，wij＝wji表明si和sj之间的相互空间关系是相同的，wij≠wji则表明si→sj和sj→si的空间关系是不同的。空间权重矩阵w的一般形式可定义为：空间权重矩阵可分为0-1型和数值型两大类，0-1型权重矩阵是指根据度量准则元素值取0或1，数值型权重矩阵元素值则可以取一般数值。1.0-1型空间权重矩阵可分为邻接型、阈值距离型等类型。邻接型权重矩阵依据空间对象之间是否具有公共边和/或公共顶点分别取0或1，邻接型包括一阶邻接和高阶邻接。阈值距离型指空间对象之间的距离与指定的阈值距离进行比较以决定取0或1。(1)邻接型空间权重矩阵①一阶rook型邻接矩阵定义为：②一阶bishop型邻接矩阵③一阶queen型邻接矩阵一阶rook型、bishop型、queen型邻接分别如图2(a)～2(c)所示，其中填色单元即是中心单元对应的一阶邻接单元。④高阶邻接矩阵在一阶邻接矩阵的基础上，可以定义高阶邻接矩阵。以二阶邻接矩阵为例，空间单元一阶邻接(直接邻接)单元的一阶邻接(直接邻接)单元构成二阶邻接单元，二阶rook型邻接、二阶queen型邻接分别如图3(a)～3(b)所示，其中填色单元即是中心单元对应的二阶邻接单元。一般地，n阶邻接矩阵由n-1阶邻接矩阵的一阶邻接矩阵构成。(2)阈值距离型邻接矩阵阈值距离型邻接矩阵考虑在一定距离下的邻接性，认为指定阈值距离内的空间对象存在邻接性，超过阈值距离则不存在邻接性。定义为：其中的距离可以是欧式普通距离、欧式加权距离、曼哈顿距离、切比雪夫距离等形式。2.数值型空间权重矩阵数值型空间权重矩阵包括k最近邻权重距离、cliff-ord权重距离和dacey权重距离等形式。(1)k最近邻权重矩阵选取最邻近的k个距离计算权重，其它距离权重为0，k值需预先设定。定义为：其中，dij为空间对象si和sj之间的距离；m为指数，常取1或2，与距离相比，距离平方反映的空间关系强度变化速率更快。(2)cliff-ord权重矩阵其一般形式定义为：其中，dij为空间对象si和sj之间的距离；βij为si和sj共享边界长度占si边界总长度的比例；a、b为指数。(3)dacey权重矩阵dacey权重矩阵除考虑空间距离和共享边界长度外，还考虑空间对象的相对面积，定义为：wij＝cij·αi·βij(10)其中，cij为对应的0-1型邻接矩阵元素，取值为0或1；αi为空间对象si的面积占研究区域所有空间对象总面积的比例；βij为si和sj共享边界长度占si边界总长度的比例。将空间权重矩阵进行行标准化，使得各行元素之和为1。行标准化公式为：行标准化的意义在于矩阵第i行的各元素值(除wii外，wii＝0)可以作为度量其它地理对象sj对si影响大小的权重因子。wij越接近于1说明sj对si的影响权重越大，当wij接近于0时，说明sj对si的影响权重可以忽略不计，由此定义了各地理对象与其空间相关地理对象之间的权重关系。步骤二：建立融合空间权重矩阵的支持向量回归模型；给定n个地理对象{si}的观测数据集{(xi,yi)}，xi∈rd，yi∈r，则融合空间权重矩阵的支持向量回归模型在回归函数中融合空间相关信息，目的是使回归函数不仅考虑各空间对象si本身的解释因素而且考虑其空间相关对象的解释因素wi.代表空间权重矩阵的第i行，则回归函数可写为：其中，ω表示权系数向量；表示输入空间到特征空间的映射函数；b表示常数项；i表示单位阵；w表示行标准化后的空间权重矩阵；x＝[x1,x2,…,xn]t；ρ表示x与wx的相关系数。ρ由下式确定：其中，cov(y，wy)表示n个地理对象的因变量y＝[y1,y2,…,yn]t与空间相关对象的因变量wy的协方差；σy、σwy分别表示y、wy的标准差。需要说明的是，在支持向量机理论中，是输入空间到特征空间的非线性映射函数，ω是特征空间中的权向量，支持向量回归模型实际上将输入空间中的非线性回归问题转变为特征空间中的线性回归问题(即对非线性映射进行线性加权)。对于地理数据回归问题，输入空间是地理对象集合s的属性空间，输入空间中的地理数据非线性回归问题yi≈f(xi,wijxj,wijyj)利用核函数映射到特征空间转变为形式如公式(12)的线性回归问题后，处于地理空间中的地理对象{si}位置、拓扑结构等空间特征并未发生改变，即空间关系保持不变性，因此并未影响到空间权重矩阵的表达，图4表达了输入空间、特征空间、地理空间三者之间的关系。步骤三：利用最小二乘支持向量回归方法求解支持向量回归模型；具体步骤为：步骤1，依据统计学习理论，支持向量回归模型的目的是使结构风险和经验风险同时达到最小，融合空间权重矩阵的支持向量回归模型公式(12)对应的优化问题为：其中，表示结构风险，结构风险描述回归模型的复杂度，复杂度小的模型可以降低回归的过拟合风险，提高模型的泛化能力；表示经验风险，经验风险描述模型与观测数据的拟合程度，在最小二乘支持向量回归方法中，经验风险用误差平方和表示，ei∈r表示误差项，经验风险越小模型的拟合精度越高；γ表示正则化参数，正则化参数用于均衡结构风险和经验风险的关系，使模型同时保持拟合精度和泛化能力。在最小二乘支持向量回归方法中，误差项ei等于观测数据yi与回归模型计算值之差，因此优化函数须满足等式约束条件：步骤2，利用拉格朗日乘子法将上述含约束条件公式(15)的优化函数(14)转化为无约束条件的拉格朗日函数，拉格朗日函数为：整理为：其中αi是拉格朗日乘子。根据kkt条件，该拉格朗日函数的最优解条件为：利用上述最优解条件方程组(18)的第1、3方程解得变量ω和ei：消去方程组(18)第2、4方程中的ωt、ei，则由第2、4方程组成的剩余方程组为：其中，j＝1,2,…,n。用符号b记剩余方程组(22)中的(i+ρw)t((i+ρw)(i+ρw)t)-1(i+ρw)。步骤3，结合mercer条件定义核函数：其中k(xi，xj)是核函数，可取线性、多项式、高斯等核函数。则剩余方程组(22)可写成矩阵形式：其中，i表示单位阵，α＝[α1，α2，…，αn]t，y＝[y1，y2，…yn]t。记方程组的解如下：则最终的融合空间权重矩阵的支持向量回归模型为：步骤四：采用均方误差、动态相似率两种评价指标对融合模型的回归性能进行度量。采用两种性能评价指标：均方误差mse(meansquareerror)和动态相似率dsr(dynamicsimilarityrate)。mse是模型输出值与真实值之间误差平方的均值，dsr反映模型输出值的变化趋势与真实趋势的接近程度。对于回归模型，设真实值为y＝{y1,y2,…,yn}，模型输出值为则各性能指标定义为：1.均方误差msemse越小，模型输出值与真实值越接近。2.动态相似率dsr其中，是y的均值，是的均值。当dsr＝0时表示输出值与输出均值相同；当dsr＝1时表示输出值与真实值的变化趋势完全一致，但并不一定表示输出值与真实值相同。下面通过对比实施例进行说明：实施例1：columbuscrime数据集columbuscrime数据集是美国哥伦布市49个区域单元的犯罪数据集，数据来源：https://geodacenter.asu.edu/sdata。地理区域单元个数n＝49，因变量为每个区域的属性变量crime，解释变量为该区域的属性变量hoval、inc，属性变量含义见表1。表1columbuscrime数据集属性变量采用全局moran’si指数对属性crime进行空间自相关性度量，moran’si公式为：其中，n是地理单元个数；xi是第i个单元的属性值，这里指crime；是n个单元的属性均值；wij是空间权重矩阵w的元素。采用一阶queen型邻接矩阵，属性crime的全局moran’si＝0.500，moran’si散点图如图5所示，基于随机性零假设计算的z得分值为z＝5.589，z得分及相应p值的概率分布情况如图6所示，moran’si及z值表明属性crime的空间分布具有显著的聚集模式，且这种聚集模式由于随机性产生的可能性小于1％。对于回归分析，moran’si及z值表明作为49个样本的空间单元属性变量crime并不满足独立性假设，任一空间单元因变量crime的变化不仅依赖于其本身自变量属性hoval、inc的变化，而且依赖于空间权重矩阵w反映的空间相关单元属性变量hoval、inc的变化，因此非线性回归分析采用融合空间权重矩阵的支持向量回归模型较为合适。采用常规最小二乘支持向量回归模型作为对比模型，记常规模型为ls-svr，并记融合空间权重矩阵的支持向量回归模型为geols-svr。将49个样本的数据集随机划分为训练集和测试集，随机选取30个样本作为训练集，用于对模型求解，剩余19个样本作为测试集，用于对模型的回归性能进行检验和对比评价。对于geols-svr，空间权重矩阵采用与计算moran’si指数相同的一阶queen型邻接矩阵，利用公式(13)计算的相关系数ρ＝0.684，核函数采用高斯核函数。表2是测试集ls-svr模型、geols-svr模型的mse、dsr指标计算结果，图7(a)～7(b)分别是测试集因变量crime的真实值和常规ls-svr模型、geols-svr模型计算输出值对比图，图中横坐标序号是对19个测试属性crime真实值从大到小排序之后的序号。表2columbuscrime测试集ls-svr、geols-svr模型mse、dsr结果模型msedsrls-svr71.1660.858geols-svr15.2140.892结合表2和图7(a)～7(b)，geols-svr模型的mse为15.214，远小于常规ls-svr模型的71.166，表明geols-svr模型的拟合精度明显提高，geols-svr模型的dsr值为0.892，相比于常规ls-svr模型的0.858，更接近于1，说明geols-svr模型的拟合结果不仅精度更高、与真实值的变化趋势也更接近，对比图7(b)与图7(a)模型输出值点的分布情况也能看出，图7(b)的geols-svr模型输出值更接近于真实值连成的折线。实施例2：bostonhousing数据集bostonhousing数据集是美国波士顿地区506个街区(censustract)房屋价格数据，数据来源：https://archive.ics.uci.edu/ml/datasets/housing。地理单元个数n＝506，因变量为每个街区的房屋价格属性变量medv，解释变量为与medv相关的该街区12个数值型属性变量，各属性变量具体含义见表3。表3bostonhousing数据集属性变量采用一阶queen型邻接矩阵，属性medv的全局moran’si＝0.584，moran’si散点图如图8所示，相应的z＝22.295，p<0.0001，表明属性medv的空间分布具有显著的聚集模式，且这种模式由于随机性产生的可能性小于0.01％。将506个样本的数据集随机划分为训练集和测试集，随机选取样本总数的2/3，即338条样本作为训练集，剩余168条样本作为测试集。对于geols-svr，空间权重矩阵采用一阶queen型邻接矩阵，相关系数ρ＝0.778，核函数采用高斯核函数。表4是bostonhousing测试集ls-svr、geols-svr的mse、dsr计算结果，图9(a)～9(b)分别是medv真实值和ls-svr、geols-svr计算输出值对比图。表4bostonhousing测试集ls-svr、geols-svr模型mse、dsr结果模型msedsrls-svr6.4410.841geols-svr1.9450.946结合表4和图9(a)～9(b)，表明相比于常规ls-svr模型，geols-svr模型的拟合结果精度更高，且与真实值的变化趋势更接近。实施例3：elect数据集elect数据集是1980年美国总统大选3107个县(county)的选举数据，数据来源：http://www.spatial-econometrics.com/data/contents.html。地理单元个数n＝3107，因变量为每个县的投票人口比例castingvotesratio，解释变量为与之相关的属性变量collegedegreesratio、homeownershipratio、percapitaincome，各属性变量具体含义见表5。表5elect数据集属性变量采用一阶queen型邻接矩阵，因变量属性castingvotesratio的全局moran’si＝0.608，moran’si散点图如图10所示，相应的z＝56.912，p<0.0001，表明属性castingvotesratio的空间分布具有显著的聚集模式，且这种模式由于随机性产生的可能性小于0.01％。将3107个样本的数据集随机划分为训练集和测试集，随机选取样本总数的2/3，即2075条样本作为训练集，剩余1032条样本作为测试集。对于geols-svr，空间权重矩阵采用一阶queen型邻接矩阵，相关系数ρ＝0.726，核函数采用高斯核函数。表6是elect测试集ls-svr、geols-svr的mse、dsr计算结果，图11(a)～11(b)分别是属性castingvotesratio真实值和ls-svr、geols-svr计算输出值对比图。表6elect测试集ls-svr、geols-svr模型mse、dsr结果模型msedsrls-svr0.00600.493geols-svr0.00520.505结合表6和图11(a)～11(b)，同样表明，与常规ls-svr模型相比，geols-svr模型的回归性能更优。综合上述3个实施例的性能评价指标mse、dsr结果，可以认为，对于地理数据的非线性回归分析，与常规ls-svr模型相比，融合空间相关性的geols-svr回归模型不仅拟合精度更高，而且与真实值的变化趋势更接近。上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。当前第1页12