适用于电力系统中长时间尺度的准稳态变步长仿真方法与流程

本发明属于电力系统仿真
技术领域：
，特别涉及一种适用于电力系统中长时间尺度的准稳态变步长仿真方法，具体说是采用准稳态仿真方法对电力系统进行建模，将电力系统数学模型中微分方程的求解分为两个阶段，快变阶段采用固定小步长的改进欧拉法求解，慢变阶段采用变步长的隐式梯形积分方法求解。
背景技术：
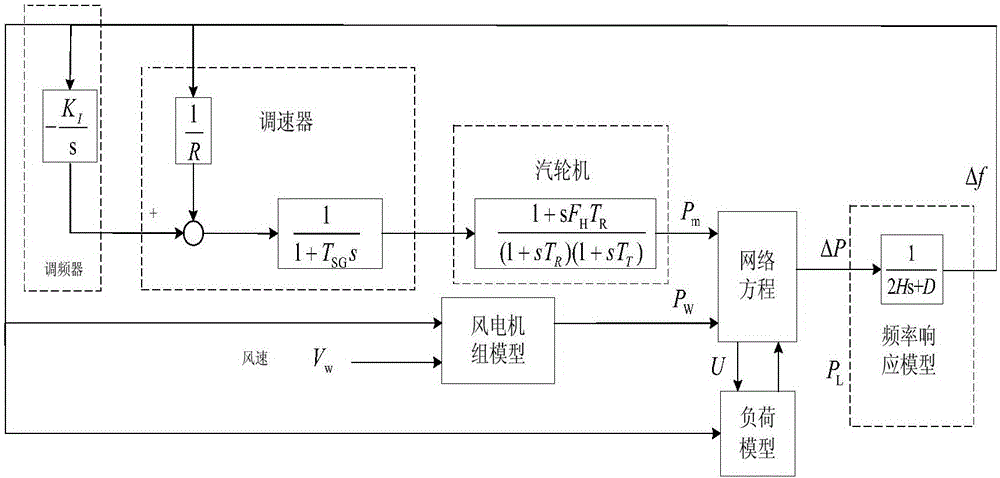
：通常，把波动时间是几秒至几十秒的动态过程称为短期暂态稳定，一般采用全时域仿真方法进行仿真；把波动时间是几十秒至几分钟的动态过程称为长期暂态稳定，由于全时域仿真方法对于全部的元件都是使用详细的模型，仿真的步长比较小，具有比较慢的仿真速度，因此，全时域仿真方法不适合应用于长期暂态稳定研究。为了解决长期暂态稳定仿真计算量巨大的问题，1998年，比利时T.V.Cutsem最早提出准稳态方法进行仿真，该方法是把暂态过程采用准稳态平衡方程进行代替，主要考虑中长期动态变化的过程。通常在稳定问题研究中，电力系统的动态模型能够表示为：0＝g(x,y,z)(1)x·=f(x,y,z)---(2)]]>z(t+1)＝h(x,y,z(t))(3)方程(1)为代数方程，代表网络方程；方程(2)表示了电网各元件的状态于控制的过程；方程(3)为离散时间的方程。方程中的x、y、z分别表示状态变量、系统代数量构成的向量、离散量。准稳态仿真方法把状态变量x分成一个变化比较快速的变量x1与一个变化比较慢的变量x2，这里假设变化比较快的变量变化无限快，所以可以采用代数方程对微分方程进行代替，所以电力系统的动态模型可以表示为：0＝g(x1,x2,y,z)(4)0＝f1(x1,x2,y,z)(5)x·2=f1(x1,x2,y,z)---(6)]]>z(t+1)＝h(x1,x2,y,z(t))(7)上式中，式(4)表示网络方程，式(5)表示系统中变化比较快的暂态过程，式(6)与式(7)表示系统中长期动态的过程。准稳态仿真将较小的时间常数忽略，只保留了较大的时间常数，加快了系统仿真速度，但准稳态仿真方法通常采用改进欧拉法求解微分方程，系统稳定性较低，且改进欧拉法限制了仿真的步长，使仿真步长不能过大，因此，采用准稳态仿真进行电力系统中长时间尺度仿真的仿真时间仍较长。电力系统中针对不同的动态过程仿真有不同的仿真方法，主要分为中长期动态过程、机电暂态过程和电磁暂态过程等三类仿真过程。本发明采用的准稳态中长期动态仿真是将电力系统慢速度的中长期动态过程与快速的机电暂态过程统一仿真。电力系统动态过程可采用非线性代数方程组(描述系统网络状态)和非线性微分方程组(描述系统中元件的动态过程)来表示，系统在慢变过程中为典型的刚性系统。以线性常系数系统为例：该系统解的形式为：其中是特征解，φ(t)是一个特解。λi为矩阵A的特征值，其实部大于零为解的增长因子，小于零为解的衰减因子，1/|Reλi|为系统时间常数，若Reλi<0，则1/|Reλi|时间内，特征解衰减1/e倍；λi的虚部表明解的周期性振动。若系统满足：Re(λi)<0(i＝1,2,…,N)(8)s=max1≤i≤N|Re(λi)|/min1≤i≤N|Re(λi)|>>1---(9)]]>s称作刚性比，若系统s>>1，则系统为病态，对应的方程式病态方程。一般s≥10就认为系统是刚性的，且s越大系统病态越严重。刚性的实质为需求解的解是变化缓慢的，但由于快速衰减的解在求解过程中带来扰动，使缓慢变化的解计算困难，从而带来数值稳定性和收敛性的问题。电力系统仿真模拟了受到扰动之后系统中动态元件和控制的过渡过程，为时域仿真。时域仿真从数学角度来看就是使用合适的数值积分方法对微分代数方程组进行求解。求解常微分方程数值积分算法稳定指的是有扰动(如舍入误差、截断误差和初始误差等)情况下，累积误差在求解过程中不会随积分步数增多而变大。稳定性问题为数值积分算法求解算法中常遇到的问题，本身稳定的系统如果仿真结果是不稳定的，原因通常为积分步长太大导致误差积累。通常采用固定步长的改进欧拉法进行准稳态仿真的求解，设仿真步长为h，特征值为λ，改进欧拉算法的绝对稳定区间分别为0<h<-2/λ。当步长大于-2/λ时，改进欧拉算法是不稳定的。因此，改进欧拉算法的步长被大大限制，仿真通常只能采用较小的步长，限制了仿真速度。准稳态仿真将较小的时间常数忽略，只保留了较大的时间常数，加快了系统仿真速度，但准稳态仿真方法通常采用改进欧拉法求解微分方程，系统稳定性较低，且改进欧拉法限制了仿真的步长，使仿真步长不能过大，因此，采用准稳态仿真进行电力系统中长时间尺度仿真的仿真时间仍较长。为了克服电力系统中长时间尺度的准稳态仿真方法存在的不足，本发明提供了一种基于准稳态仿真的变步长隐式积分和小步长显示积分交替进行的仿真方法，通过变步长隐式积分和小步长显式积分相结合，既提高了系统的仿真速度，也提高了数值算法的稳定性。技术实现要素：本发明的目的是提出一种适用于电力系统中长时间尺度的准稳态变步长仿真方法，其特征在于，包括如下步骤：步骤1：建立系统准稳态仿真模型；步骤2：采集系统稳态数据，包括母线有功功率、母线无功功率、机端有功功率和发电机端电压；步骤3：输入系统稳态数据，包括母线有功功率、母线无功功率、机端有功功率、发电机端电压和仿真参数；步骤4：输入系统中元件的参数，包括变压器参数、励磁系统参数、线路参数和发电机参数；步骤5：依据输入系统的稳态数据和元件参数进行潮流计算，得到系统稳态运行下的参数，包括发电机输出的电磁功率、系统节点电压；步骤6：依据第(5)步潮流计算结果，给准稳态仿真系统状态变量赋初值x(0)；步骤7：将仿真时间设置为t＝0，设置仿真步长为最小值，开始系统暂态稳定性计算；步骤8：依据系统状态变量变化率的大小选择仿真方法，当时，系统处在快变阶段，采用固定步长的显式改进欧拉法进行计算，执行步骤9；当时，系统处于慢变阶段，采用变步长的隐式梯形积分法进行计算，执行步骤10；其中m为频率变化率临界值，取m＝2.8×10‐3；式中，x(n)为第n个状态变量；步骤9：采用固定步长的改进欧拉算法进行计算；步骤10：采用变步长的隐式梯形积分法进行计算。步骤11：本时刻计算成功，计算下一时刻，令t＝t+h；式中，h为仿真步长；步骤12：判断仿真时间t是否大于设定的仿真时间T，若t<T，则执行步骤7，若t>T，则执行步骤13。步骤13：计算完成，输出计算结果。所述步骤9中采用固定步长的改进欧拉算法进行计算的步骤为：步骤9.1：设k1＝0，k1为改进欧拉法迭代次数；步骤9.2：求解系统网络方程，计算节点电压；步骤9.3：求解系统微分方程，计算状态变量的微分量；步骤9.4：求解系统代数方程，计算系统状态量；步骤9.5：k1＝k1+1，迭代次数k1加1；步骤9.6：判断迭代次数k1是否小于2，若小于2，利用欧拉方程更新状态变量将计算的节点电压、状态变量带入，执行步骤9.2；若k1大于2，则使用改进欧拉法更新系统状态变量则执行步骤11；式中，h为仿真步长、xn为第n次迭代状态变量的值，yn为第n次迭代代数量的值，f函数为微分方程；所述步骤10的采用变步长的隐式梯形积分法进行计算步骤如下：步骤10.1：设隐式梯形积分法迭代次数k2＝0；步骤10.2：求解系统网络方程，计算节点电压；步骤10.3：求解系统微分方程，计算状态变量的微分量；步骤10.4：求解系统代数方程，计算系统状态量；步骤10.5：k2＝k2+1，迭代次数k2加1；步骤10.6：判断k2是否大于最大迭代次数，若大于则执行步骤10.9，若小于则执行步骤10.7；步骤10.7：计算截断误差式中，En+1为截断误差，Ck+1为常数，k为迭代k次，为解xn+1的第k+1阶导数；为解xn+1的第k+1阶导数。步骤10.8：判断截断误差是否大于容许误差，如果大于容许误差，则执行步骤10.2，如果小于容许误差，则执行步骤10.9.步骤10.9：采用隐式梯形积分公式更新系统状态变量，式中，xn+1为n+1时刻状态变量x的值，为n+1时刻状态变量x第k次迭代值；步骤10.10：根据系统状态变量变化率的大小进行变步长。步骤10.11：判断仿真步长是否达到设定的最大、最小步长，若大于最大步长，则步长为设定的最大步长，若小于最小步长，则步长为最小步长。本发明有益效果：本发明的适用于电力系统中长时间尺度的准稳态变步长仿真方法，在准稳态仿真程序的基础上，考虑了电力系统仿真多时间尺度的特点，按状态变量变化率大小将仿真过程分为快变阶段和慢变阶段，快变阶段采用固定步长的改进欧拉法进行求解，慢变阶段采用变步长的隐式梯形积分法进行求解。本发明在满足系统仿真数值精度与数值稳定性要求的前提下，进一步提高了准稳态仿真方法的计算速度，大大缩短了仿真时间，改变了之前准稳态仿真步长较小，仿真时间较长，而步长过大，仿真系统稳定性较差的缺点。附图说明图1为适用于电力系统中长时间尺度的准稳态变步长仿真方法流程图；图2为准稳态仿真系统频率响应模型；图3为双馈风机模型示意图；图4为双馈风机准稳态仿真模型；图5为内蒙古某地实际系统算例结构图；图6为准稳态仿真模型和详细模型仿真运行结果对比；图7为本发明的方法与步长不变的准稳态仿真方法运行结果对比；图8为本发明方法仿真的频率变化率；图9为本发明方法仿真的步长变化；图10为阶梯型扰动时本发明的方法与步长不变的准稳态仿真方法运行结果对比；图11为阶梯型扰动时本发明的方法仿真的频率变化率；图12为阶梯型扰动时本发明的方法仿真的步长变化；表1为本发明的方法与步长不变的仿真方法的仿真时间对比；表2为阶梯型扰动时本发明与步长不变的仿真方法的仿真时间对比。具体实施方式本发明提出一种适用于电力系统中长时间尺度的准稳态变步长仿真方法，下面结合附图和实施例对本发明作更进一步的说明。图1所示为适用于电力系统中长时间尺度的准稳态变步长仿真方法流程图；该仿真方法包括如下步骤：步骤1：建立系统准稳态仿真模型；步骤2：采集系统稳态数据，包括母线有功功率、母线无功功率、机端有功功率和发电机端电压；步骤3：输入系统稳态数据，包括母线有功功率、母线无功功率、机端有功功率、发电机端电压和仿真参数；步骤4：输入系统中元件的参数，包括变压器参数、励磁系统参数、线路参数和发电机参数；步骤5：依据输入系统的稳态数据和元件参数进行潮流计算，得到系统稳态运行下的参数，包括发电机输出的电磁功率、系统节点电压；步骤6：依据第(5)步潮流计算结果，给准稳态仿真系统状态变量赋初值x(0)；步骤7：将仿真时间设置为t＝0，设置仿真步长为最小值，开始系统暂态稳定性计算；步骤8：依据系统状态变量变化率的大小选择仿真方法，当时，系统处在快变阶段，采用固定步长的显式改进欧拉法进行计算，执行步骤9；当时，系统处于慢变阶段，采用变步长的隐式梯形积分法进行计算，执行步骤10；其中m为频率变化率临界值，取m＝2.8×10‐3；式中，x(n)为第n个状态变量；步骤9：采用固定步长的改进欧拉算法进行计算；步骤10：采用变步长的隐式梯形积分法进行计算。步骤11：本时刻计算成功，计算下一时刻，令t＝t+h，h为仿真步长；步骤12：判断仿真时间t是否大于设定的仿真时间T，若t<T，则执行步骤8，若t>T，则执行步骤13。步骤13：计算完成，输出计算结果。如附图5所示为内蒙某地八机二十节点电力系统，结合图1所示流程，具体说明本发明的实施过程。1.准稳态仿真模型1.1系统频率响应模型在准稳态仿真中主要考虑较长时间尺度的动态过程，所以将较小的时间常数忽略。在火电机组准稳态仿真建模中，只考虑调速器模型以及汽轮机模型，模型如图2所示。图中，Pm、Pw、PL分别为火电机组、风机和负荷功率；ΔP为风电机组、火电机组的总发电功率与系统总负荷功率差值；TSG为调速器时间常数；R为调速系数；FH为再热系数；TR为再热时间常数；TT为汽轮机时间常数；KI为二次调频增益。1.2双馈风机准稳态仿真模型如图3所示，双馈风机的详细模型包括传动轴模型、风机空气动力学模型、风力发电机模型、机侧变流器模型以及网侧变流器模型。准稳态模型中将较小的时间常数忽略，简化后风机模型只包括传动轴模型、风机空气动力学模型和桨距角控制模型，如图4。风机空气动力学模型：风机的输入功率和风速、空气密度、桨距角等因素有关，但是通常只有一部分风能可以被利用。风机机械功率数学模型为：Pwm=12AVw3ρCP(λ,β)]]>式中，A为风机有效扫风面积；Vw为风的速度；ρ为空气的密度；Cp为风功率转换系数；λ为叶尖速比，λ＝ωrR/Vw；β为机桨距角；R为风机半径；ωr为风机旋转的角速度。风能利用系数Cp(λ,β)为：Cp(λ,β)=0.22(116λ1-5-0.4β)e-12.5λ1]]>λ1=1-0.035β3+1+1λ+0.08β]]>传动轴和桨距角控制模型如图4，图中Hw是风机惯性的时间常数；Pwe、Pwm为风机的电磁功率和机械功率；ωref、ωm为风机的参考转速和实际转速。1.3负荷模型依据不同的用途，有很多种不同的负荷模型，最简单的是恒阻抗模型，该模型暂态过程中等值阻抗恒定不变，使用简单，但是该方法精度不高，本发明选用负荷的静态特性模型。负荷的静态特性模型表示了负荷吸收的功率与该节点电压和频率的关系，有较高的精度。数学模型为：PL=PL0[AP(VLVL0)2+BP(VLVL0)+CP]·(1+KP·Δf)]]>QL=QL0[AQ(VLVL0)2+BQ(VLVL0)+CQ]·(1+KQ·Δf)]]>式中，PL0、QL0为扰动前负荷吸收的有功、无功功率；VL0为扰动前节点电压。对于不同节点，参数AP、BP、CP、AQ、BQ和CQ取值通常不同，但应该满足：AP+BP+CP＝1AQ+BQ+CQ＝11.4网络结构模型暂态过程中负荷吸收的功率与该节点的电压和频率有关，因此，暂态过程中应该考虑系统网络结构。网络功率平衡方程为：EPEQEGEsys=Pmi+Pwmi-Pgridi(V,θ)-ηiQGi(δ,Ef,V,θ)+Qwei-Qgridi(V,θ)Pmi+Pwmi-PGi(δ,Ef,V,θ)-Pwei-ηiδr=0]]>式中，EP、EQ分别为N个节点注入有功、无功功率不平衡量(i＝1,…,N)，N为网络节点数；EG为m个发电机有功不平衡量，m为网络中含有火电或风电机组的节点个数；Esys为一个代数方程，指定第r个节点的功角为参考值。PG、PQ为由δ、Ef、θ、V求得的火电机组的电磁功率；Pwe、Qwe为风机电磁功率，通过电力电子设备控制得到；Pgridi与Qgridi为通过网络节点电压幅值和相角得到的输入电网的有功、无功功率；Hi为火电机组惯性时间常数。通过牛拉法求解网络功率平衡方程可得：θT(h+1)VT(h+1)δT(h+1)ηT(h+1)=J-1EP(h)EQ(h)EG(h)Esys(h)+θT(h)VT(h)δT(h)ηT(h)]]>式中，J为雅可比矩阵，如下式：J=-∂Pgrid∂θ-∂Pgrid∂V0-∂ηi∂η∂QG∂θ-∂Pgrid∂θ∂QG∂V-∂Qgrid∂V∂QG∂δ0-∂PG∂θ-∂PG∂V-∂PG∂δ-∂ηi∂η00er0]]>式中，er为m列行向量，第r列为1，其余为0。2.数值积分方法的选择数值积分方法的选择，也就是在暂态仿真过程中依据给定的条件，选择积分方式为变步长的隐式梯形积分法和固定步长的改进欧拉法中的一种。系统快变阶段采用固定步长的改进欧拉法，慢变阶段采用变步长的隐式梯形积分法。系统快变阶段也就是机电暂态过程，通常是系统发生如切机、短路等故障或风电场风速快速变化后的一段时间。状态变量值在这个阶段变化较快，有较大的变化率，若此时采用变步长的隐式梯形积分法，会使积分步长很小，增加迭代次数，求解较缓慢。因此，系统快变阶段采用固定步长的改进欧拉法，这里步长h＝0.1，在准稳态仿真中为较小的步长。系统慢变阶段也就是中长期动态过程，通常是系统没有故障发生或者风电场风速变化缓慢阶段。状态变量在这个阶段变化较缓慢，有较小的变化率，此时为刚性系统，若此时采用固定步长的改进欧拉法，则步长较小，仿真时间较长。所以，系统慢变阶段采用变步长的隐式梯形积分法，可以使仿真步长依据状态变量变化率的大小而改变，可以增大仿真步长，加快系统的仿真速度。本发明研究的准稳态仿真主要研究系统频率的变化，因此，本发明依据系统频率变化率的大小来选择，设定频率变化率临界值m。当时，系统为慢变阶段，当时，系统为快变阶段。(本发明取m＝2.8×10‐3)3.数值求解方法数值积分算法主要包括显式积分算法和隐式积分算法两类。显式积分是一个关于xn+1的直接计算公式，计算公式中不含有xn+1；而隐式积分的计算公式中含有尚未求解出的xn+1，隐式积分公式实际为关于xn+1的函数方程。显示积分如二阶、三阶、四阶显式龙格‐库塔法(常用的改进欧拉法为二阶显式龙格‐库塔法)的稳定区间是有限的，因此，步长被限定在很小的范围内；隐式积分，如梯形积分法和后退欧拉法的绝对稳定域为hλ复平面的左半平面，隐式积分的稳定区间为-∞<hλ<0、0<h<∞。对于隐式积分步长的选取仅需考虑迭代收敛性和计算的精度，而不需考虑积分算法的稳定性。显式积分算法中把系统微分方程与代数方法分别求解。由于显式积分每一步的计算公式只需前一刻的状态变量和网络方程的值，因此，能够单独求解各动态元件的微分方程，该方法有编程简单、可靠和扩张方便灵活的特点。但显式积分数值计算方法稳定性较差，需要采用较小的积分步长求解刚性系统，导致求解速度变慢。该方法存在交接误差，因此，显式积分不能较好的适应长时间的稳定计算。隐式积分每一步的计算公式不只需要前一刻的状态变量和网络方程的值，还需未知的计算时刻的状态变量和网络方程的值，因此，需要迭代求解。隐式数值计算方法的稳定区间为-∞<hλ<0、0<h<∞，所以，该方法不会因稳定性问题对积分步长产生限制，使仿真步长大大提高，提高了计算速度。常用的隐式积分为后退欧拉法和梯形积分法。3.1固定步长的改进欧拉法固定步长的改进欧拉法为一种较为常用的数值计算方法，计算较为简单，适用于系统快变阶段。对于时刻t＝tn，状态变量x＝xn，电压V＝Vn，用这些值求解t＝tn+1＝tn+h时刻的状态变量的值。首先，求解系统网络方程，θT(h+1)VT(h+1)δT(h+1)ηT(h+1)=J-1EP(h)EQ(h)EG(h)Esys(h)+θT(h)VT(h)δT(h)ηT(h)]]>由上式得到预测的电压值之后，求解系统微分方程，由式x‾n+1-xn+hf(xn,Vn)]]>得到系统状态变量的预测值求解系统的代数方程，得到系统代数量，第一次迭代完成。进行第二次迭代，由上述方法求解系统网络方程，得到t＝tn+1时刻的电压Vn+1；求解t＝tn+1时刻微分方程解的预测值从而可以根据改进欧拉法得到状态变量的校正值：xn+1=xn+h2(f(xn,Vn)+f(x‾n+1,V‾n+1))]]>此时刻迭代结束，进入下一时刻迭代。3.2隐式梯形积分法隐式梯形积分法与改进欧拉法的求解公式相似，但精度高于改进欧拉法，且隐式积分的稳定区间为-∞<hλ<0、0<h<∞，因此可以采用较大的步长进行求解，提高了仿真的速度。也是利用时刻t＝tn，状态变量x＝xn，电压V＝Vn，用这些值求解t＝tn+1＝tn+h时刻的状态变量的值。令t＝tn时刻的状态变量值和电压值为迭代初值：求解系统网络方程，θT(h+1)VT(h+1)δT(h+1)ηT(h+1)=J-1EP(h)EQ(h)EG(h)Esys(h)+θT(h)VT(h)δT(h)ηT(h)]]>由上式得到预测的电压值之后，求解系统微分方程，由式x‾n+1(1)=xn+hf(xn+1(0),Vn+1(0))]]>得到系统状态变量的预测值计算截断误差式中，为解xn+1的第k+1阶导数。Emax为最大允许误差，若En+1>Emax则重复上述步骤继续迭代，直至截断误差小于允许值，或迭代次数大于设定的最大迭代次数时停止迭代。第k次迭代得到的状态变量值和电压值为则根据隐式梯形积分法得状态变量值为：yn+1=yn+h2(f(yn,Vn)+f(y‾n+1(k),V‾n+1(k)))]]>此时刻迭代结束，进入下一时刻迭代。4.变步长对于刚性系统的求解有慢变分量与快变分量的问题，在数值积分计算中，变量变化率较大的暂态过程中，应采用小步长进行计算；而变量变化率较小的慢变过程中，可采用大步长进行计算。系统中负实部绝对值较大的特征值所对应的解变化较快时，即系统处于暂态阶段，此时系统不被称为刚性系统，而到了慢变过程，这些快变的解分量衰减成较小的值，甚至能忽略不计，这时系统才被成为刚性系统。这说明一个系统在自变量的一部分区间为刚性的，而在另外一部分区间不是刚性的。这可以较好地说明系统数字仿真与科学工程计算过程中遇到的实际问题。在暂态过程中，因为解分量变化较快，为了较好地计算数值解结果，需选取较小的步长进行计算。暂态过程中的步长选取依据精度的要求来确定。慢变过程的刚性阶段，此时快变分量已衰减到很小的值，显式数值积分方法的步长可由来确定，步长的量级应为隐式积分方法的计算步长不受稳定性问题限制，该方法步长可采用局部截断误差计算。本发明采用变步长的隐式梯形积分法，是指仿真过程中选择隐式梯形积分法时进行变步长，步长依据系统频率变化率进行变化，如下式：h=h1,m3<|dω(n)dt|h2,m2<|dω(n)dt|<m3h3,m1<|dω(n)dt|<m2h4,|dω(n)dt|<m1]]>上式为步长选择方法，其中m1<m2<m3<m4，h1<h2<h3<h4。当时采用固定步长的改进欧拉法进行求解。(本发明取m1＝0.0012、m2＝0.002、m3＝0.0028，h1＝0.1、h2＝0.2、h3＝0.3、h4＝0.4)图6将准稳态仿真方法与全时域仿真方法运行结果进行对比，准稳态仿真方法与全时域仿真方法运行结果相差较小，因此，准稳态仿真方法有较高的精度。图7可以看出，本发明的方法与准稳态仿真方法运行结果相差较小，因此，本发明的方法具有较高的精度。由图8、图9、图10和图11可以看出，暂态过程系统频率变化率较大，仿真方法采用固定步长的改进欧拉法，仿真步长较小，当系统处于慢变阶段时，系统频率变化率较小，仿真步长根据频率变化率的大小进行调整。当采用固定步长的准稳态仿真且步长超过0.3s时，系统不稳定，运行结果不收敛，而本发明的方法，快变阶段采用小步长，慢变阶段步长最大为0.4s，提高了仿真速度。表1和表2表明本发明的方法明显提高了仿真的速度。综上所述，本发明的发明既提高了系统的仿真速度，又有较好的稳定性。因此，设计结果满足要求。表1仿真30s仿真时间对比表2阶梯型扰动时仿真100s仿真时间对比当前第1页1 2 3