一种基于轴角矢量的相对定向方法与流程

本发明属于摄影测量与计算机视觉领域，特别是涉及一种基于轴角矢量的相对定向方法。

背景技术：

立体模型的相对定向是摄影测量与计算机视觉的基本问题之一，其目的是利用立体模型内在的几何关系，确定立体模型中左右两张像片的相对位置及相对姿态参数，主要用于目标几何定位及三维模型重建。在传统的相对定向中，常用欧拉角描述像片姿态，虽然几何意义表达较明显，但大量的三角函数运算将影响计算的速度和精度，且可能会出现数值解算的奇异性；此外，单位四元数有4个自由度，在描述姿态时还须附加一个约束条件，增加了求解的复杂度。考虑到任何空间旋转均可以用一个轴角对构成的轴角矢量进行描述，而且轴角矢量仅有3个独立参数，计算过程无需附加约束条件，以及具有计算速度更快、算法稳健的优势，本发明提出一种基于轴角矢量的相对定向方法。首先利用轴角矢量参数化旋转矩阵，然后建立共面条件方程，并根据参数化旋转矩阵以及反对称矩阵的性质，推导出基于轴角矢量的相对定向平差模型，最后采用间接法平差原理求解相对定向参数。

技术实现要素：

本发明针对现有技术的不足，提供一种基于轴角矢量的相对定向方法。本发明基于轴角矢量参数化旋转矩阵，利用旋转矩阵与轴角矢量微分关系以及反对称 矩阵的性质，将共面条件方程线性化，推导建立基于轴角矢量的相对定向平差模型，最后采用间接法平差原理求解相对定向参数。该方法具有计算速度快，稳健性好，数值解算精度高的特点。

本发明提供的技术方案是一种基于轴角矢量的相对定向方法，主要包括以下步骤：

一种基于轴角矢量的相对定向方法，其特征在于，包括如下步骤：

步骤1，利用轴角矢量参数化旋转矩阵，具体是：空间目标的旋转可用一个旋转轴n和一个旋转角θ组成的轴角对描述，定义矢量r＝θn＝[r1 r2 r3]^T，r称为轴角矢量或旋转矢量,r1、r2、r3为r在空间中的三个分量；轴角矢量r的方向即旋转轴的方向，它的模等于旋转角，即||r||＝θ；轴矢量的方向与旋转的方向满足右手法则；

旋转矩阵R与轴角矢量r存在如下关系：

式(1)中，为单位矩阵,Sr表示由r定义的反对称矩阵，

若给定轴角矢量r，则可利用式(1)构造参数化旋转矩阵；

此外，利用旋转轴n和旋转角θ组成的轴角对描述空间旋转，实际等价于绕旋转轴n连续旋转k次，每一次旋转θ/k；当k→∞时，可得下式：

其中，按泰勒公式展开为：

则给定轴角矢量r,可按式(1)构造旋转矩阵R，也可根据需要按式(4)用矩阵指数形式表示；

步骤2，建立旋转矩阵与轴角矢量微分关系：根据步骤1建立的旋转矩阵以及反对称矩阵的定义，建立旋转矩阵与轴角矢量微分关系；

步骤3，建立共面条件方程：立体像对中左右两张像片的相对位置及相对姿态恢复后，立体模型中所有同名光线应对对相交于模型表面，即左右两条同名光线与摄影基线满足共面条件，

步骤4，建立相对定向平差模型：在步骤3中，共面条件方程为非线性方程，将其按泰勒级数展开，可得到相对定向的线性化模型；在此基础上，利用在步骤2中建立的旋转矩阵与轴角矢量微分关系以及反对称矩阵的性质，推导并建立基于轴角矢量的相对定向平差模型；

步骤5，平差解算相对定向参数：根据步骤4建立的相对定向平差模型，利用间接平差原理，解算相对定向参数。

在上述的一种基于轴角矢量的相对定向方法，所述步骤2中，建立旋转矩阵与轴角矢量微分关系的实现方式如下：

由轴角矢量r＝[r1 r2 r3]^T定义的反对称矩阵Sr可分解为:

式(6)中，

根据式(5)、(6)可得定义Δr＝[Δr1 Δr2 Δr3]^T，得旋转矩阵与轴角矢量的微分关系式(7),

由式(7)，进一步推得旋转矩阵与轴角矢量的微分关系式(8),

dR＝RSΔr 式(8)

式(8)中，SΔr表示利用轴角矢量的微分定义的反对称矩阵,

在上述的一种基于轴角矢量的相对定向方法，所述步骤3中，建立共面条件方程的实现方式如下：

定义S1-x1y1z1、S2-x2y2z2分别表示左右像片的像空间坐标系，a1(x1,y1,-f)、a2(x2,y2,-f)分别表示同名像点的像空间坐标；立体像对中左右两张像片的相对位置及相对姿态恢复后，立体模型中所有同名光线应对对相交于模型表面，即左右两条同名光线与摄影基线共面；令立体模型基线为矢量左投影光线为右投影光线为三个矢量共面满足关系式(10)：

定义根据式(10)，共面条件方程可表示为：

其中，(xl,yl,zl)、(xr,yr,zr)表示同名像点的像空间辅助坐标；R分别为左、右像片的旋转矩阵。

在上述的一种基于轴角矢量的相对定向方法，所述步骤4中，建立相对定向平差模型的实现方式如下：

式(11)为非线性方程，视bY,bZ,xr,yr,zr为未知数，将其按泰勒级数展开，得到相对定向线性化模型如下：

式(14)中，F0由相对定向元素的近似值根据式(11)求得，dbY,dbZ,dxr,dyr,dzr为相对定向未知参数的改正数；各偏导数分别为：

在式(14)两边同时除以并令c0＝1，整理后得相对定向误差方程式：

式(17)中，

式(18)中，N1、N2分别表示左右投影系数，Q表示相对定向时模型点的上下视差，若Q＝0，则表示相对定向已完成；若Q≠0，则表示相对定向未完成，模型点仍存在上下视差；

对式(13)两边取微分可得，根据步骤2中推得的旋转矩阵微分关系式(8)dR＝RSΔr，可得：

设由反对称矩阵性质可知，则可得像点坐标与轴角矢量的微分关系式：

将式(20)代入式(17)，并令则相对定向误差方程为：

式(21)即为利用轴角描述的严密的相对定向平差模型，其中平差解算的未知数类型分别为：描述像片相对位置的基线分量改正数dbY,dbZ；描述像片相对姿态关系的轴角矢量的改正数Δr1,Δr2,Δr3。

在上述的一种基于轴角矢量的相对定向方法，所述步骤5中，平差解算相对定向参数的实现方式如下：

在步骤4中，式(21)可改写为间接法平差误差方程的一般形式：

vi＝Ai·Δx-li,pi 式(22)

式(22)中：

vi表示第i个模型点上下视差改正数残差；

表示第i个模型点误差方程系数矩阵；

li＝Q，表示第i个模型点误差方程常数项；

Δx＝[dby dbz Δr1 Δr2 Δr3]^T,表示相对定向未知参数；

由于式(22)中有5个未知数dbY,dbZ,Δr1,Δr2,Δr3，因此，完成相对定向参数的解算至少需要量测5对以上的同名像点的像点坐标；

观测n对同名像点，可按式(22)列出n个误差方程，其矩阵形式为：

根据最小二乘原理，组成法方程:

(A^TPA)Δx＝(A^TPL) 式(24)

法方程的解为：

Δx＝(A^TPA)^-1(A^TPL) 式(25)

由于共面条件方程式(11)是非线性的，因此，上述相对定向参数的求解是一个逐步趋近的迭代过程；每次迭代时用未知参数近似值与迭代计算的改正数之和作为新的近似值，重复计算步骤3-5，求出新的改正数，这样反复趋近，直到未知参数改正数小于规定的限差δ时，迭代终止，相对定向计算结束；迭代时，未知参数近似值的更新过程如下：

X^γ+1＝X^γ+Δx^γ+1，(γ＝0,1,…) 式(26)

其中，Δx^γ+1表示第γ+1次迭代得到的相对定向未知参数的改正数；γ＝0时，X⁰表示第一次迭代前相对定向未知参数的初始值，X^γ为第γ次迭代时相对定向未知参数的近似值，X^γ+1表示第γ+1次迭代时相对定向未知参数的近似值。

本发明具有如下优点：本发明利用轴角矢量构造旋转矩阵，充分利用了反对称矩阵的性质，得到的数学模型严密、形式简洁，不仅避免了传统平差解算欧拉角参数时可能出现的奇异性问题，而且在平差解算时，仅涉及一个旋转角的正、余弦三角函数运算，大大地降低了计算费用。

附图说明

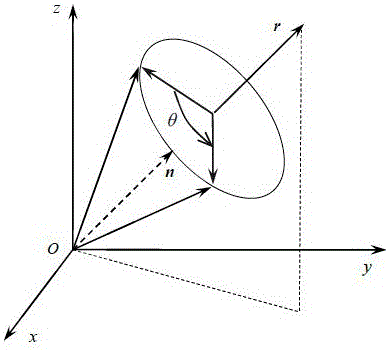
图1为本发明实施例轴角矢量示意图。

图2为本发明实施例的共面条件示意图。

具体实施方式：

本发明提供一种基于轴角矢量的相对定向方法，首先利用轴角矢量参数化旋转矩阵，然后建立共面条件方程，并根据参数化的旋转矩阵以及反对称矩阵的性质，推导出基于轴角矢量的相对定向平差模型，最后采用间接法平差原理求解相对定向参数。

下面结合附图和实施例对本发明的技术方案作进一步说明。

步骤1，利用轴角矢量参数化旋转矩阵

空间目标的旋转可以用一个旋转轴n(单位矢量)和一个旋转角θ组成的轴角对进行描述(如图1)。定义矢量r＝θn＝[r1 r2 r3]^T，r称为轴角矢量或旋转矢量。轴角矢量r的方向即旋转轴的方向，它的模等于旋转角，即||r||＝θ。轴矢量的方向与旋转的方向满足右手法则。

由Rodriguez公式可知，旋转矩阵R与轴角矢量r存在如下关系：

式(1)中，Sr表示由r定义的反对称矩阵，

若给定轴角矢量r，则可利用式(1)构造参数化旋转矩阵。

此外，利用旋转轴n(单位矢量)和旋转角θ组成的轴角对描述空间旋转，实际等价于绕旋转轴n(单位矢量)连续旋转k次，每一次旋转θ/k。当k→∞时，可 得下式：

其中，按泰勒公式展开为：

综合式(1)、(4)可知：给定轴角矢量r,可以按式(1)构造旋转矩阵R，也可根据需要按式(4)用矩阵指数形式表示，因此，可得下式：

步骤2，建立旋转矩阵与轴角矢量微分关系

由轴角矢量r＝[r1 r2 r3]^T定义的反对称矩阵Sr可分解为:

式(6)中，

根据式(5)、(6)可得定义Δr＝[Δr1 Δr2 Δr3]^T，得旋转矩阵与轴角矢量的微分关系式(7),

由式(7)，进一步推得旋转矩阵与轴角矢量的微分关系式(8),

dR＝RSΔr 式(8)

式(8)中，SΔr表示利用轴角矢量的微分定义的反对称矩阵,

式(8)将在本发明实施例步骤4中使用。

步骤3，建立共面条件方程

如图2，S1-x1y1z1、S2-x2y2z2分别表示左右像片的像空间坐标系，a1(x1,y1,-f)、a2(x2,y2,-f)分别表示同名像点的像空间坐标。立体像对中左右两张像片的相对位置及相对姿态恢复后，立体模型中所有同名光线应对对相交于模型表面，即左右两条同名光线与摄影基线共面。令立体模型基线为矢量左投影光线为右投影光线为三个矢量共面满足关系式(10)：

设根据式(10)，共面条件方程可表示为：

其中，(xl,yl,zl)、(xr,yr,zr)表示同名像点的像空间辅助坐标；R分别为左、右像片的旋转矩阵，可根据本发明实施例步骤1计算得到。

步骤4，建立相对定向平差模型

式(11)为非线性方程，视bY,bZ,xr,yr,zr为未知数，将其按泰勒级数展开，得到 相对定向线性化模型如下：

式(14)中，F0由相对定向元素的近似值根据式(11)求得，dbY,dbZ,dxr,dyr,dzr为相对定向未知参数的改正数，各偏导数分别为：

在式(14)两边同时除以并令c0＝1，整理后得相对定向误差方程式：

式(17)中：

式(18)中，N1、N2分别表示左右投影系数，Q表示相对定向时模型点的上下视差，若Q＝0，则表示相对定向已完成；若Q≠0，则表示相对定向未完成，模型点仍存在上下视差。

对式(13)两边取微分可得，根据步骤2中推得的旋转矩阵微

分关系式(8)dR＝RSΔr，可得：

设由反对称矩阵性质可知，则可得像点坐标与轴角矢量的微分关系式：

将式(20)代入式(17)，并令则相对定向误差

方程为：

式(21)即为利用轴角描述的严密的相对定向平差模型，其中平差解算的未知数类型分别为：描述像片相对位置的基线分量改正数dbY,dbZ；描述像片相对姿态关系的轴角矢量的改正数Δr1,Δr2,Δr3。

步骤5，平差解算相对定向参数

在步骤4中，式(21)可改写为间接法平差误差方程的一般形式：

vi＝Ai·Δx-li,pi式(22)

式(22)中：

vi表示第i个模型点上下视差改正数残差；

表示第i个模型点误差方程系数矩阵；

li＝Q，表示第i个模型点误差方程常数项；

Δx＝[dby dbz Δr1 Δr2 Δr3]^T,表示相对定向未知参数。

由于式(22)中有5个未知数dbY,dbZ,Δr1,Δr2,Δr3，因此，完成相对定向元素的解算至少需要量测5对以上的同名像点的像点坐标。

观测n对同名像点，可按式(22)列出n个误差方程，其矩阵形式为：

根据最小二乘原理，组成法方程:

(A^TPA)Δx＝(A^TPL) 式(24)

法方程的解为：

Δx＝(A^TPA)^-1(A^TPL) 式(25)

由于共面条件方程式(11)是非线性的，因此，上述相对定向参数的求解是一个逐步趋近的迭代过程；每次迭代时用未知参数近似值与迭代计算的改正数之和作为新的近似值，重复计算步骤3-5，求出新的改正数，这样反复趋近，直到未知参数改正数小于规定的限差δ时，迭代终止，相对定向计算结束；迭代时，未知参数近似值的更新过程如下：

X^γ+1＝X^γ+Δx^γ+1，(γ＝0,1,…) 式(26)

其中，Δx^γ+1表示第γ+1次迭代得到的相对定向未知参数的改正数；γ＝0时，X⁰表示第一次迭代前相对定向未知参数的初始值，X^γ为第γ次迭代时相对定向未知 参数的近似值，X^γ+1表示第γ+1次迭代时相对定向未知参数的近似值。

本文中所描述的具体实施例仅仅是对本发明精神作举例说明。本发明所属技术领域的技术人员可以对所描述的具体实施例做各种各样的修改或补充或采用类似的方式替代，但并不会偏离本发明的精神或者超越所附权利要求书所定义的范围。