动态弦截法计算不平衡张力的方法与流程

文档序号：11155836阅读：858来源：国知局

本发明属于高压输电线路技术领域，具体涉及一种动态弦截法计算不平衡张力的方法。

背景技术：

高压输电线路架线完成时，直线杆塔前后侧水平张力相等，但当气象条件发生改变或电线断线时，由于档距、高差、荷载等不同，导致直线杆塔前后侧水平张力不等，产生了不平衡张力。准确计算不平衡张力是校验杆塔强度，校核电线不均匀覆冰、上人检修等情况下的相间间隙、交叉跨越距离等的基础，所以准确而快速地计算各种工况下的不平衡张力，对实际工程有重要意义。

目前，针对电线不平衡张力计算，国内外学者进行了诸多研究，例如有限元分析模型等，由于算法复杂，计算量大，不适用于实际工程。广泛应用于实际工程的等线长法，由于其公式复杂，直接求解非线性方程组非常困难，所以工程实际中主要应用试凑法，直到满足精度要求。试凑法虽然简单，编程让计算机完成试凑也很容易，但是步长较长，试凑法无法保证有解，步长太短，计算速度又太慢。针对试凑法步长很难选择的缺点，有关文献中提出了二分法，在一定程度上加快了试凑效率，但是简单的二分法还是具有一定的盲目性。

技术实现要素：

本发明的目的是提供一种动态弦截法计算不平衡张力的方法，为实际工程的不平衡张力批量计算提供一种新的快速计算方法。

本发明的技术方案具体为：

一种动态弦截法计算不平衡张力的方法，包括以下步骤：

1)设独立耐张段内有连续i档，架线时气象条件为无风、无冰、气温t_m，架线完成后，档内所有悬垂串均保持垂直，当出现不平衡条件时，各档应力不等，档内悬垂串发生倾斜，得出第i档档距增量Δl_i与档内应力σ_i之间的关系式如下：

式中：l_i是第i档档距，m，β_i为第i档高差角；α为电线线膨胀系数，E为电线弹性系数，t_m、σ_m、γ_m分别为架线时气温、水平应力、电线比载，t、σ_i、γ_i分别为计算不平衡张力时气温、水平应力、电线比载，Δt_e为架线时考虑初伸长降低的等效温度；

由于档距相邻档出现了不平衡张力差，导致悬垂串发生了倾斜，假设悬垂串为均匀荷载，则第i+1档档内应力σ_i+1与档距增量Δl_i关系式如下：

式中：σ_i、σ_i+1为第i档、i+1档档内电线水平应力，δ_i为第i基直线杆塔上悬垂串挂线点偏距，δ_i＝Δl₁+Δl₂+…+Δl_i，λ_i、G_i分别为第i基直线杆塔悬垂串串长、荷载，h_i、h_i+1是第i档、i+1档高差，m，β_i、β_i+1为第i档、i+1档高差角，l_i、l_i+1是第i档档距；

一个独立耐张段内，各档档距增量之和应为零，即：

2)将总档距增量δ_i与第一档假设初始应力σ₁函数关系设为

δ_i＝f(σ₁)，

获取上述导线参数、各档数据、气象条件；

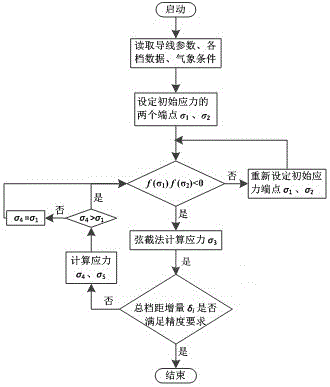
3)根据弦截法对应力进行求解，首先设定初始应力的两个端点值σ₁、σ₂作为计算应力的区间[σ₁、σ₂]，其中σ₁是区间最小值，按经验值设定；σ₂是区间最大值，设为导线最大张力；

4)根据上述关系式验证公式f(σ₁)f(σ₂)＜0，确定所求应力在设定的初始应力[σ₁,σ₂]区间内；

5)通过设定的初始应力σ₁、σ₂的值，用弦截法计算应力σ₃作为端点值，进一步缩小所求应力的范围；

6)将总档距增量δ_i的精度设为10^-3，将应力σ₃代入关系式δ_i＝f(σ₁)，得到的总档距增量δ_i满足精度要求，则运算结束。

所述步骤4)不成立，则返回步骤3)，重新设定初始应力的两个端点值σ₁、σ₂，继续验证计算。

所述步骤6)中总档距增量δ_i不满足精度要求，继续用弦截法计算初始应力σ₄、σ₅，以[σ₄，σ₅]作为所求应力的区间范围，验证得到的应力σ₄>σ₁，把进一步计算得到的初始应力σ₄、σ₅代入步骤4)中运算，再依次进行第5)和6)步骤的操作。

计算得到的应力σ₄>σ₁不成立时，则程序默认应力σ₄＝σ₁，把计算得到的应力σ₄、σ₅替代设定的初始应力σ₁、σ₂作为初始应力代入步骤4)运算，再依次进行第5)和6)步骤的操作。

与现有技术相比，本发明提出了动态弦截法计算不平衡张力，以一种动态的割线法，快速查找准确值，并将计算过程编辑成程序，大大提高了不平衡张力的批量计算效率，更加适用于工程实际计算。

附图说明

图1是本发明程序流程图。

图2是动态弦截法原理示意图。

具体实施方式

动态弦截法首先以弦截法为基础，如图2所示，通过端点x₁、x₂之间的连线，找到点x₃；然后通过对x₁、x₃连线，找到点x₄；通过对x₂、x₃连线，找到点x₅。此时，已经找到了弦截法两个新端点x₄、x₅，重复以上方法，直到找到准确解。需要注意，总档距增量与第一档应力在并非单调函数，当计算出x₄处应力小于x₁时，此时x₄处的应力是背离准确值的，应舍弃，继续让x₁点参与下次弦截。

如图1所示，根据动态弦截法原理，本发明提供一种动态弦截法计算不平衡张力的方法，包括以下步骤：

由于档距相邻档出现了不平衡张力差，导致悬垂串发生了倾斜，假设悬垂串为均匀荷载，则第i+1档档内应力σ_i+1与档距增量Δl_i关系式如下：

一个独立耐张段内，各档档距增量之和应为零，即：

2)将总档距增量δ_i与第一档假设初始应力σ₁函数关系设为

δ_i＝f(σ₁)，

获取上述导线参数、各档数据、气象条件；

4)根据上述关系式验证公式f(σ₁)f(σ₂)＜0，确定所求应力在设定的初始应力[σ₁，σ₂]区间内；

5)通过设定的初始应力σ₁、σ₂的值，用弦截法计算应力σ₃作为端点值，进一步缩小所求应力的范围；

6)将总档距增量δ_i的精度设为10-³，将应力σ₃代入关系式δ_i＝f(σ₁)，得到的总档距增量δ_i满足精度要求，则运算结束。

所述步骤4)不成立，则返回步骤3)，重新设定初始应力的两个端点值σ₁、σ₂，继续验证计算。

所述步骤6)中总档距增量δ_i不满足精度要求，继续用弦截法计算初始应力σ₄、σ₅，以[σ₄，σ₅]作为所求应力的区间范围，验证得到的应力σ₄＞σ₁，把进一步计算得到的初始应力σ₄、σ₅代入步骤4)中运算，再依次进行第5)和6)步骤的操作。

计算得到的应力σ₄＞σ₁不成立时，则程序默认应力σ₄＝σ₁，把计算得到的应力σ₄、σ₅替代设定的初始应力σ₁、σ₂作为初始应力代入步骤4)运算，再依次进行第5)和6)步骤的操作。

以浙江～福州1000kV交流线路工程不均匀覆冰导致的不平衡张力为算例，应用不平衡张力“等线长法”模型，并引入动态弦截法，通过已编制好的软件进行计算。