一种深海缓波型脐带缆的非线性静态分析方法与流程

本发明涉及一种深海缓波型脐带缆的非线性静态分析方法。

背景技术：

深海油气开采工程中，脐带缆作为水下生产系统重要组成部分，起到连接水面浮式装置和海底油井的重要作用，是海洋油气水下生产系统的生命线。随着海洋油气开采工程不断向深海推进，脐带缆由于水深增大导致顶端所受的拉力不断增加。为了避免深水脐带缆顶端拉力过大，缓波构型由于有效减小顶端拉力这一特性被广泛应用于深水油气开发。然而，缓波构型中浮力块体系的引入致使其非线性特性愈发明显，因此有必要对深水缓波型脐带缆进行非线性静态分析。

技术实现要素：

为了克服已有技术无法有效分析深水缓波型脐带缆的不足,本发明提供了一种有效实现深水缓波型脐带缆分析的深海缓波型脐带缆的非线性静态分析方法。

本发明解决其技术问题所采用的技术方案是：

一种深海缓波型脐带缆的非线性静态分析方法，包括以下步骤：

步骤一：理论假设，条件如下：

1.1)不考虑船体的耦合作用，忽略风荷载影响；

1.2)仅考虑海流的拖曳水动力作用，不考虑波浪作用；

1.3)海床简化为水平文克尔地基梁模型，即海床的垂直抵抗力简化为一系列线弹簧作用；

1.4)脐带缆材料各向同性，始终处于弹性阶段，且忽略轴向变形影响；

1.5)该力学分析为平面内分析，即二维分析；

步骤二：建立力学分析模型

脐带缆由于其细长特性，根据经典杆理论以脐带缆管道中心轴线位置描述其位形，划分为：

悬跨段，从下放点LOP到触地点TDP之间的管段，由悬浮段L₁、浮力块段L₂以及下降着地段L₃三部分组成；

触地段，管道触地点TD)之后置于海床上的管段；。

根据上述深水脐带缆缓波型划分，建立两个坐标系分别对悬跨段和触地段进行力学分析：整体坐标系(x,y)以下放点(LOP)为该坐标系原点，用以分析悬跨段力学特性；局部坐标系(x₁,y₁)以触地点(TDP)为该坐标系原点，用以分析触地段力学特性；

步骤三：设定边界条件

脐带缆通过限弯器连接于水面浮式装置，将其连接简化为铰接连接，从而确定下放点LOP的边界条件；考虑脐带缆的直径影响，确定触地点处TDP的边界条件；

步骤四：数值求解

在求解过程中脐带缆顶端拉力T₀、悬跨段长度以及触地点位置都是未知量，仅顶端下放角θ₀为已知参数，需要通过迭代运算进行数值求解；

一旦顶端拉力T₀确定，通过递推法从顶端依次计算出每一微分单元的构型，从而求解出脐带缆缓波型的整体形态。

进一步，所述方法还包括以下步骤：

步骤五：有限元模型验证：使用有限元软件OrcaFlex建模与理论方法进行对比分析。

本发明的有益效果主要表现在：(1)基于悬链线理论和小变形梁理论，综合考虑海洋环境荷载以及弹性海床地基作用，有较高的正确性和可靠性(2)对于缓波型脐带缆安装分析提供了一种简单有效的方法(3)可以对缓波型脐带缆安装进行一系列敏感性分析，为实际的安装作业提供参考。

附图说明

图1为缓波型脐带缆受力分析图。

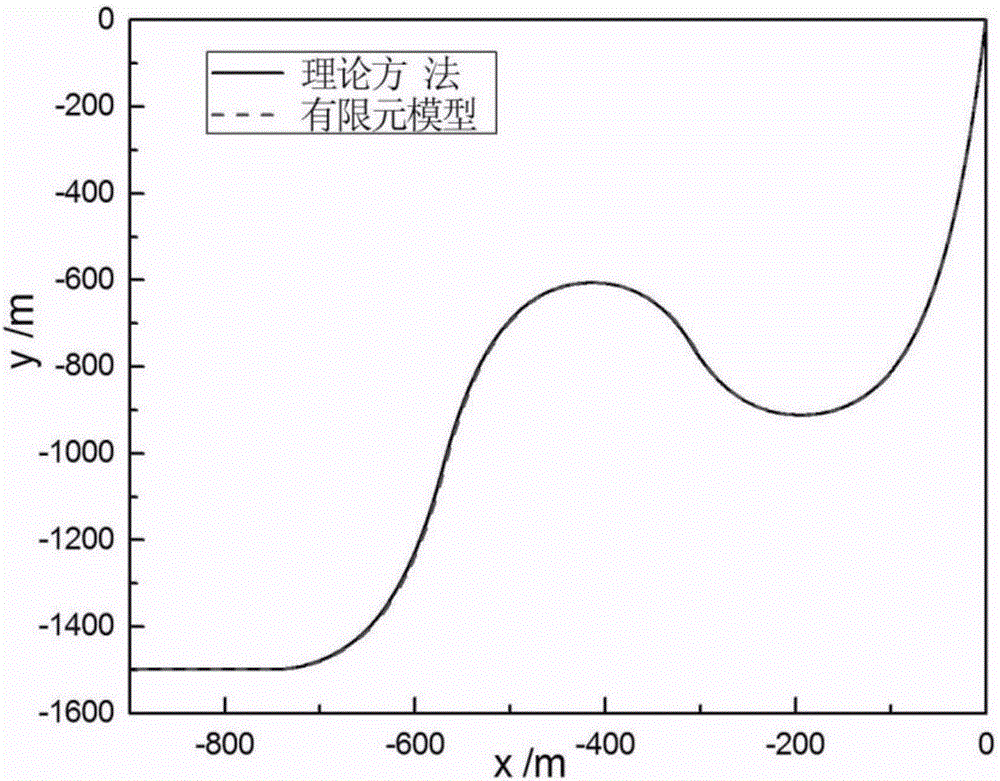
图2为缓波型脐带缆形态对比图。

图3为沿脐带缆长度弯矩对比图。

图4为沿脐带缆长度轴力对比图。

图5为悬跨段管段微元受力分析示意图。

图6为触地段管段微元受力分析示意图。

图7为数值计算流程图。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图7，一种深海缓波型脐带缆的非线性静态分析的方法，包括以下步骤：

步骤一：理论假设

实际安装工程中，由于受到海床、风浪流以及船体运动的影响，深水缓波型脐带缆的非线性静态分析比较复杂。为了便于理论分析研究，做以下简单假设：

1.1)不考虑船体的耦合作用，忽略风荷载影响。

1.2)仅考虑海流的拖曳水动力作用，不考虑波浪作用。

1.3)海床简化为水平文克尔地基梁模型，即海床的垂直抵抗力可简化为一系列线弹簧作用。

1.4)脐带缆材料各向同性，始终处于弹性阶段，且忽略轴向变形影响。

1.5)该力学分析为平面内分析，即二维分析。

步骤二：建立力学分析模型

脐带缆由于其细长特性，根据经典杆理论以脐带缆管道中心轴线位置描述其位形。图1为典型的深水脐带缆缓波型布置，本方法将脐带缆分为两个部分进行研究分析：

悬跨段，从下放点(LOP)到触地点(TDP)之间的管段，由悬浮段L₁、浮力块段L₂以及下降着地段L₃三部分组成；

触地段，管道触地点(TDP)之后置于海床上的管段。

根据上述深水脐带缆缓波型划分，建立两个坐标系分别对悬跨段和触地段进行力学分析：整体坐标系(x,y)以下放点(LOP)为该坐标系原点，用以分析悬跨段力学特性；局部坐标系(x₁,y₁)以触地点(TDP)为该坐标系原点，用以分析触地段力学特性。

步骤三：设定边界条件

由于实际安装工程中，脐带缆通过限弯器连接于水面浮式装置，将其连接简化为铰接连接，从而确定下放点LOP的边界条件。考虑脐带缆的直径影响，确定触地点处TDP的边界条件。

步骤四：数值求解

在求解过程中脐带缆顶端拉力T₀、悬跨段长度以及触地点位置都是未知量，仅顶端下放角θ₀为已知参数，需要通过迭代运算进行数值求解。一旦顶端拉力T₀确定，可以通过递推法从顶端依次计算出每一微分单元的构型，从而求解出脐带缆缓波型的整体形态。

步骤五：有限元模型验证

为了验证理论方法的正确性和可靠性，使用有限元软件OrcaFlex建模与理论方法进行对比分析。图2至图4为理论方法和有限元模拟的对比结果：图2为脐带缆形态对比图；图3为沿脐带缆长度弯矩对比图；图4为沿脐带缆长度轴力对比图(脐带缆长度以下放点LOP为起始位置)。从图中可以看到，理论方法和有限元模拟的形态、弯矩以及轴力吻合得相当好。

悬跨段模型：如图5所示，悬跨段的脐带缆主要由悬浮段、浮力块段以及下降着地段三部分组成。其中浮力块均匀分布于浮力块段，用以提供一定程度的升力效应，形成拱形构造。由于浮力块段附着着均匀分布的浮力块，为方便计算需对浮力块段的单位浮重和外直径等进行等效简化。此外，由于浮力块的长度一般小于其间距，故不考虑其对浮力块段抗弯刚度的增强作用。水流方向以水平向右为正，反之为负。将缓波型的悬跨段划分成若干个微分管段单元，通过微分单元的力学平衡得到如下公式：

dV＝F_τds sinθ-F_nds cosθ-wds (1)

dH＝F_nds sinθ+F_τds cosθ (2)

dM＝Vdscosθ-Hdssinθ-w(ds)²cosθ/2-F_n(ds)²/2 (3)

其中，T、V、H分别为管段的轴力、垂直力以及水平力；dV、dH分别为管段垂直力和水平力的增量；dM为管段的弯矩增量；F_n、F_τ分别是作用在单位长度管段上的水动力在法向和切向的分力；C_d、C_τ分别为法向和切向水动力系数；ρ_w为海水密度；D为管段外径，浮力块段等效外径为D₂，其余为D₁；w为管道单位长度的浮重，浮力块段等效单位浮重为w₂，其余为w₁；V_c为水流速度；ds为管段长度；θ为管段与水平方向的夹角。

从式(3)可以看出弯曲刚度对缓波型脐带缆构型的影响十分复杂，但由于缓波型脐带缆主要用于深水作业，故可以忽略脐带缆的弯曲刚度，采用悬链线理论对悬跨段进行力学分析。由于不考虑悬跨段脐带缆的弯曲刚度，故各微分单元与水平方向的夹角θ以及夹角增量dθ可以通过式(3)忽略高阶项推导得到：

一旦微分单元与水平方向的夹角θ求得，忽略管段的轴向变形可以得到各微分单元在x、y轴的增量为：

dx＝ds cosθ，dy＝ds sinθ (9)

上述计算脐带缆缓波型悬跨段的形态时基于忽略脐带缆的弯曲刚度的假设，将脐带缆简化为缆绳进行力学分析。实际的悬跨段脐带缆承受弯矩荷载，脐带缆弯矩根据梁理论推导公式如下：

触地段模型：图6为脐带缆触地段的受力模型，主要受到海床垂直抵抗力以及触地点作用力，忽略海床的轴向摩擦力。以脐带缆触地点处为局部坐标系原点，由于考虑管道的直径影响，该坐标系的原点位于海床平面以上的管道半径处。

触地段管道的埋深是决定管道海底稳性的重要决定因素。因此有必要研究触地段的力学特性和埋深情况。为了便于分析，将海床简化为文克尔地基梁模型，即海床的垂直抵抗力可以简化为一系列线弹性弹簧作用。由于触地段脐带缆变形较小，根据小变形线性梁理论，脐带缆在触地段的微分方程可表示为：

其中，T是脐带缆在TDP处的轴向拉力。由于忽略海床的轴向摩擦，脐带缆触地段的轴向拉力可以近似为一个常数，且等于T。式(11)为四阶常微分方程：当时，该方程没有实数解；当时，上述微分方程的通解为：

其中，c₁、c₂、c₃和c₄为未知系数，

当x₁→∞时，管道由于只受到自身重力和浮力的影响，即y₁＝w/k。因此，式(12)中的系数c₃，c₄都等于零，触地段的表达式可简化为：

脐带缆触地段的弯矩可以利用小变形梁理论推导求得：

边界条件：由于实际安装工程中，脐带缆通过限弯器连接于水面浮式装置，将其连接简化为铰接连接，下放点LOP的边界条件：

y(x＝0)＝0 (15)

θ(x＝0)＝θ₀ (16)

M(x＝0)＝0 (17)

考虑脐带缆的直径影响，触地点处TDP的边界条件：

y₁(x₁＝0)＝0 (18)

θ⁺_TDP＝θ^-_TDP (19)

M⁺_TDP＝M^-_TDP (20)

T⁺_TDP＝T^-_TDP (21)

其中θ⁺_TDP、M⁺_TDP和T⁺_TDP分别表示局部坐标系(x₁,y₁)中触地点处的倾角、弯矩和轴力；θ^-_TDP、M^-_TDP和T^-_TDP分别表示整体坐标系(x,y)中触地点处的倾角、弯矩和轴力。

数值求解：该数值求解方法可以归纳为以下几个步骤。首先需要假设一个顶端拉力值T₀，然后从管道顶端开始递推求解，将管道划分成n份等长度微分单元ds(每一微分单元长度一般取0.1m)，运用公式(22-28)进行求解计算出各点的位移和受力状态，直至触地点(y_i≥W_D-D/2)停止递推计算。若是始终无法计算到触地点，则说明T₀假设过小，需重新假设计算。根据边界条件求解式(13)得到触地段的解析解，其中触地点处的轴力可由整体坐标系的悬跨段触地点轴力等效得到。方程(13)中有两个未知数c₁和c₂，可根据边界条件(18)和(19)求得这两个未知数。由于顶端拉力T₀为假设值，并非真实值，无法保证触地点处弯矩连续，即无法保证边界条件(20)。因此，可由悬跨段和触地段在触地点处弯矩连续的条件|M⁺_TDP-M-_TDP|/M⁺_TDP<ε(其中ε是一个非常小的值)来判断T₀的真实值。一旦脐带缆悬跨段顶端拉力确定，就可求解出缓波型脐带缆的形态以及内力分布。具体求解过程如图7所示。

V_i＝V_i-1+F_τds sinθ-F_nds cosθ-wds (22)

H_i＝H_i-1+F_nds sinθ+F_τds cosθ (23)

θ_i＝arctan(V_i/H_i) (25)

x_i＝x_i-1+dscosθ_i-1 (26)

y_i＝y_i-1+ds sinθ_i-1 (27)