一种基于Coq的MSVL程序验证方法与流程

本发明属于程序验证技术领域，尤其涉及一种基于Coq的MSVL程序验证方法。

背景技术：

定理证明和模型检测是两种当前主流的形式化验证技术。与模型检测相比，定理证明技术可以处理具有无穷状态空间的程序或系统，且不会引起状态爆炸的问题。然而，用户需要指导证明过程并直接干预中间步骤，因此用户的主观性被引入证明中。目前存在许多定理证明器，例如，Coq、PVS、ACL2、HOL、Isabelle等。作为一个证明开发系统，Coq提供了一个描述数学定义、算法以及定理的形式化语言Gallina和一个用于半自动化证明的开发环境。事实上，它提供了交互式证明方法、决策和半决策算法以及一个允许用户可以定义自己的证明方法的策略语言。同时它也允许用户使用外部的代数系统或定理证明器。作为一个用于数学形式化或程序开发的平台，Coq在高阶符号表达、隐式表达和宏方面提供了支持。目前，Coq被广泛地用于验证领域。MSVL是一个集建模、仿真和验证于一体的时序性逻辑程序设计语言，它可以很好的用于并行和实时系统的规范化和验证。它包含了大多数程序语言都必须的基本语句，例如，赋值语句、顺序语句、分支语句、循环语句、并行语句和投影语句等。MSVL基于一个可以用来描述和解释多核并行程序的计算模型(CCM)，同时，异步通信机制也已被实现，从而可以进行分布式系统的建模和验证。为了增加MSVL的可用性和实用性，原子类型如整型、实型、字符型、字符串、链表、数组、指针、结构等被实现来定义多类型值、函数和谓词。由于模型检测方法完全自动化且可以快速得到验证结果，因此目前关于MSVL的大多数可用验证工具都基于模型检测。而定理证明方法需要用户和定理证明器在证明过程中进行交互，即半自动的证明。故相对于模型检测方法，定理证明方法在证明过程中对用户的要求较高，验证过程也较复杂，所以关于MSVL程序的定理证明方面还没有很好的工具来支持。

技术实现要素：

本发明的目的在于提供一种基于Coq的MSVL程序验证方法，旨在解决利用定理证明器进行MSVL程序性质的半自动化证明问题。

本发明是这样实现的，一种基于Coq的MSVL程序验证方法，所述基于Coq的MSVL程序验证方法使用Coq规范语言Gallina描述MSVL的语法和语义；使用Coq规范语言描述MSVL的公理系统。

进一步，所述MSVL的语法和语义，包括变量、表达式、语句及其缩写形式；MSVL的公理系统，包括状态上和区间上的公理以及推理规则。

进一步，所述缩写使用MSVL语句定义的衍生结构。

进一步，在性质的验证过程中，将用MSVL对实例的建模结果和抽取出的相关性质转化为待证定理，然后人工选择合适的策略链，每执行一个策略，当前目标会被转化为一个或多个待证的子目标，继续选择并执行直到没有待证明的子目标，即证明结束，性质验证完成。

进一步，所述基于Coq的MSVL程序验证方法包括以下步骤：

步骤一，使用Coq的规范语言Gallina描述MSVL变量、表达式以及函数；

步骤二，使用Coq的规范语言Gallina定义MSVL语句及其导出公式；

步骤三，在Coq中对MSVL公理系统中的公理和推导规则进行形式化定义。

进一步，所述使用Coq的规范语言Gallina描述MSVL变量、表达式以及函数，采用Gallina的归纳类型来定义，归纳类型需要指定归纳集合的名字和类型以及归纳谓词的构造子，Coq的类型检查器会验证每个构造子的类型是否正确；对于函数的定义使用递归类型来构造递归函数。

进一步，所述使用Coq的规范语言Gallina定义MSVL语句及其缩写，使用Gallina定义语句和缩写；语句利用归纳类型定义，缩写利用Coq的记号结构来完成；一个记号是一个用来表示表达式或公式的符号缩写。

本发明的另一目的在于提供一种利用所述基于Coq的MSVL程序验证方法的定理证明器。

本发明提供的基于Coq的MSVL程序验证方法，利用Coq强大的数学模型基础和完整的工具集来形式化MSVL公理系统，从而使得Coq能够识别MSVL程序；对使用MSVL建模的程序或系统，通过定理证明技术验证系统性质；可以将程序建模和抽取出的相关性质在Coq中转化成待证定理，通过人工选择合适的Coq策略链来指导证明的进行，从而完成性质的验证；琐碎的细节可以利用Coq策略自动的证明，人工仅在复杂的步骤上指导控制，有效地简化了MSVL程序的定理证明过程。

附图说明

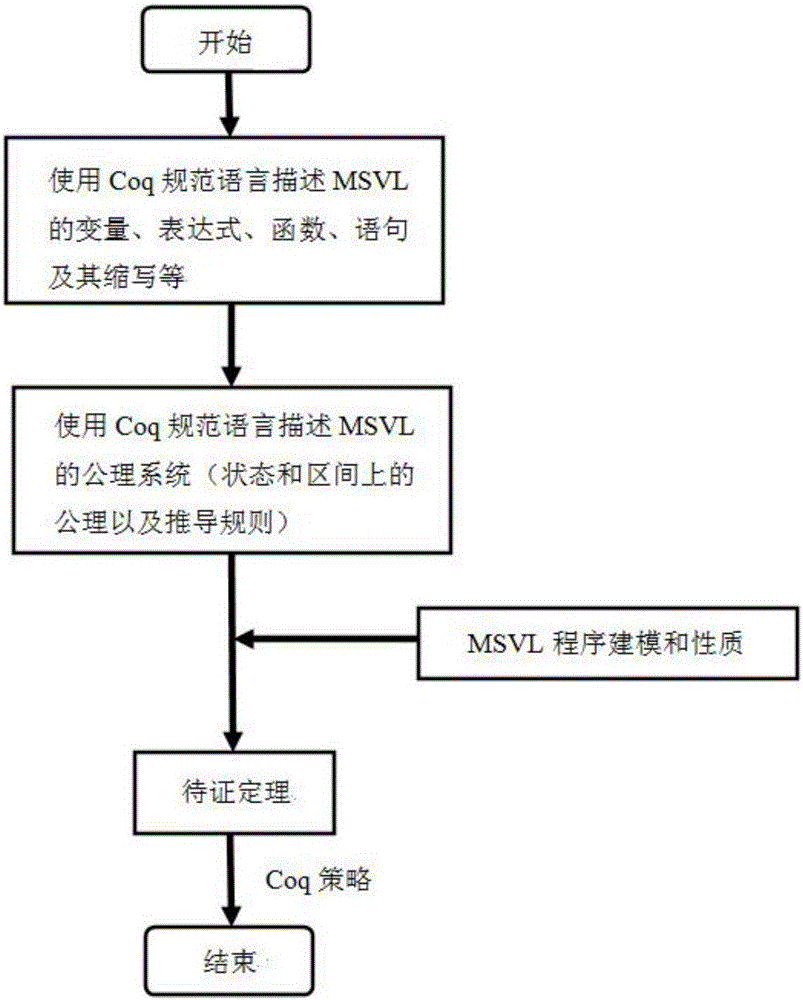
图1是本发明实施例提供的基于Coq的MSVL程序验证方法流程图。

图2是本发明实施例提供的实施例1的整体实现流程图。

图3是本发明实施例提供的使用该证明系统对系统性质进行验证的示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

下面结合附图对本发明的应用原理作详细的描述。

如图1所示，本发明实施例提供的基于Coq的MSVL程序验证方法包括以下步骤：

S101：使用Coq的规范语言Gallina描述MSVL变量、表达式以及函数；

S102：使用Coq的规范语言Gallina定义MSVL语句及其导出公式；

S103：在Coq中对MSVL公理系统中的公理和推导规则进行形式化定义；

在本发明的实施例中：

所述使用Coq的规范语言Gallina描述MSVL变量、表达式以及函数，采用Gallina的归纳类型来定义，归纳类型需要指定归纳集合的名字和类型以及归纳谓词的构造子，Coq的类型检查器会验证每个构造子的类型是否正确。对于函数的定义，必要时可以直接使用递归类型来构造递归函数。定义可以看作对一个名称的形式化解释，定义后该名称可被Coq系统接受且被实际定义在任何时候进行替换，前提是定义的类型等正确。而递归类型通常被用于定义递归函数，这种情况下参与递归的变量必须是归纳类型。

所述使用Coq的规范语言Gallina定义MSVL语句及其缩写，仍然使用Gallina定义语句和缩写。语句利用归纳类型定义，缩写利用Coq的记号结构来完成。一个记号是一个用来表示表达式或公式的符号缩写。

所述在Coq中对MSVL公理系统中的公理和推导规则进行形式化定义，这些公理和推导规则会在证明过程中和策略一块指导证明的进行。因此，这三部分是紧密联系，相辅相成。

下面结合具体实施例对本发明的应用原理作进一步的描述。

实施例1：

参照图2，本发明实施例的实现步骤如下：

步骤1：使用Coq规范语言描述MSVL的变量、表达式、函数、语句及其缩写等。

变量和原子命题在Coq中实现如下：

Inductive Var：Set：＝var：Z-＞Var.

Inductive Ap：Set：＝prop：nat-＞Ap.

Var和Ap分别代表MSVL变量和原子命题，使用归纳类型定义。

算术表达式和布尔表达式定义如下：

其中，n是一个有类型的常数，x是一个变量，f是一个m元函数，p是一个原子命题，e_i是算术表达式。

算术表达式和布尔表达式在Coq中实现如下：

Inductive Aexp：Set：＝

AInt：Z-＞Aexp

|AId：Var-＞Aexp

|ANext：Aexp-＞Aexp

|APre：Aexp-＞Aexp

|APlus：Aexp-＞Aexp-＞Aexp

|AMinus：Aexp-＞Aexp-＞Aexp

|AMult：Aexp-＞Aexp-＞Aexp

|AMod：Aexp-＞Aexp-＞Aexp.

Inductive Bexp：Set：＝

|BTrue：Bexp

|BFalse：Bexp

|BNot：Bexp-＞Bexp

|BAnd：Bexp-＞Bexp-＞Bexp

|BEq：Aexp-＞Aexp-＞Bexp

|BLe：Aexp-＞Aexp-＞Bexp.

在Coq中Aexp和Bexp分别表示算术表达式和布尔表达式，使用归纳类型定义。

状态、区间以及区间上的部分函数在Coq中实现如下：

使用记录类型定义状态state，归纳类型定义区间Interval，同时定义了一些区间上的常用操作函数如区间连接函数Concatenation。

MSVL基本语句定义如下：

例如，empty语句表示当前状态是程序执行区间的最后一个状态；nextp语句表示程序p在下一状态执行；alw p表示程序p从当前状态开始的所有状态都会执行；顺序语句p；q表示程序p和q是顺序执行的，程序p从当前状态开始到未来的某个时刻，然后q再执行；条件语句ifb then p else q表示当b成立时p执行，否则q执行。

MSVL基本语句在Coq中的实现如下所示：

Inductive st：Set：＝

|Emp：st

|Ass：Var-＞Aexp-＞st

|Pass：Var-＞Aexp-＞st

|SF：Var-＞st

|IFr：Var-＞st

|Coj：st-＞st-＞st

|Sec：st-＞st-＞st

|Nex：st-＞st

|Alw：st-＞st

|Cond：Bexp-＞st-＞st-＞st

|Exqu：Var-＞Ap-＞st

|Sequ：st-＞st-＞st

|Whi：Bexp-＞st-＞st

|Para：st-＞st-＞st

|Pro：list st-＞st-＞st

|Syn：Bexp-＞st.

步骤2：使用Coq规范语言描述MSVL的公理系统(状态和区间上的公理和推导规则)。

MSVL公理系统示例如下：

基于之前的工作，例如，公理A4和A7可以被表达为：

Axiom A4：forall p：st，

|-(Alw((Coj(Alw p)Emp)＜＝＞(Coj p Emp))).

Axiom A7：forall p q：st，

|-(Alw((Sequ(Nex p)q)＜＝＞Nex(Sequ p q))).

对某个系统的性质证明过程参照图3：

1)使用MSVL对系统建模；

2)抽取出待证明的相关性质；

3)基于Coq的MSVL证明系统来得到待证明的定理，可能需要一些辅助引理的定义和证明。然后针对当前待证目标人工选择合适策略来将其转化为其它待证的子目标，继续该过程直到没有子目标，即定理证明完成，从而性质得到验证。

在证明时，每一步证明的推进都是通过人工输入合适的策略完成。策略实现了反向推理，即已知当前目标来得到策略作用后产生的子目标，也就是说一个策略使得目标被化简为它的子目标。然而，并不是每一个规则或公理都适用于当前目标，也不是每一个策略都可被用来化简当前目标，所以在对当前目标应用某个策略前，Coq系统会自动检查规则或公理的前提条件是否满足。如果不满足，则该策略不能被选择，产生错误。

因此，策略和规则的选择在证明时很重要，很大程度上需要根据当前目标以及需要产生的子目标来定。而证明的结束也意味着性质验证的完成。

下面结合具体的应用对本发明的应用原理作进一步的描述。

验证实例-青蛙跳荷叶；问题描述：6只青蛙，7片荷叶，每个青蛙处于一片荷叶上。初始状态是三只黄青蛙在左边，三只绿青蛙在右边，两组青蛙被一片荷叶隔开。每个青蛙可以跳一步或隔一个青蛙跳两步到一片空荷叶上。问题是是否可以找到一条移动路径使得两组青蛙互换位置？

建模：其为该问题在MSV中使用MSVL的建模结果。因为青蛙跳跃遵循一定规则，所以总是可以到达一个时刻使得所有青蛙都不能移动，即解空间可以看作是一个子集树。所以使用一个数组p来表示荷叶以及数组值代表青蛙状态，值为1表示黄青蛙，2表示绿青蛙，0表示荷叶上无青蛙，可以通过仿真来查看建模的正确性。

性质：令初始状态为s0＝[1，1，1，0，2，2，2]，s1＝[2，2，2，0，1，1，1]，则待证性质为[](s0→◇s1)，即[]((p[0]＝1∧p[1]＝1∧p[2]＝1∧p[3]＝0∧p[4]＝2∧p[5]＝2∧p[6]＝2)→◇(p[0]＝2∧p[1]＝2∧p[2]＝2∧p[3]＝0∧p[4]＝1∧p[5]＝1∧p[6]＝1))

验证：需要先定义一些辅助函数，函数的正确性在Coq中可以验证。

其次，定义出青蛙的跳跃规则，从而保证状态的正确转换。待证定理为：

Lemma Jump：

|-(Alw(Imp

(Coj(Coj(Coj(Coj(Coj(Coj(Coj(Ass empty_pos(AInt 3))

(Ass stone0(AInt 1)))(Ass stone1(AInt 1)))

(Ass stone2(AInt 1)))(Ass stone3(AInt 0)))

(Ass stone4(AInt 2)))(Ass stone5(AInt 2)))

(Ass stone6(AInt 2)))

(Coj(Coj(Coj(Coj(Coj(Coj(Coj(Ass empty_pos(AInt 3))

(Ass stone0(AInt 2)))(Ass stonel(AInt 2)))

(Ass stone2(AInt 2)))(Ass stone3(AInt 0)))

(Assstone4(AInt 1)))(Ass stone5(AInt 1)))

(Ass stone6(AInt 1))))).

手动输入策略，Coq环境的右上方会显示出当前待证的子目标。

综上所述，本发明提出的基于Coq的MSVL定理证明方法，能够很好的用来验证MSVL系统性质，具有良好的正确性和可靠性。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。